Анимации градиентного спуска и ландшафта потерь нейронных сетей на Python

Во время изучения различных алгоритмов машинного обучения я наткнулся на ландшафт потерь нейронных сетей с их горными территориями, хребтами и долинами. Эти ландшафты потерь сильно отличались от выпуклых и гладких ландшафтов потерь, с которыми я столкнулся при использовании линейной и логистической регрессий. Здесь мы создадим ландшафты потерь нейронных сетей и анимированного градиентного спуска с помощью датасета MNIST.

Рисунок 1 — Ландшафт потерь свёрточной нейронной сети с 56 слоями (VGG-56, источник)

---

На приведённом выше изображении показан ландшафт нейронной сети с высокой степенью поверхностных потерь. Ландшафт потерь — это визуальное представление значений, которые функция стоимости берёт на себя для заданного диапазона значений параметров с учётом наших тренировочных данных. Поскольку нашей целью является визуализация затрат в трёх измерениях, необходимо выбрать два конкретных параметра, которые будут варьироваться в наших графиках, тогда как все остальные параметры модели остаются неизменными. Стоит, однако, отметить, что существуют более продвинутые методы (например, уменьшение размерности, нормализация фильтра), которые могут использоваться для приближения ландшафтов потерь нейронной сети в подпространстве с низкой размерностью. Трёхмерное представление ландшафта потерь нейронной сети VGG с 56 слоями показано на рисунке 1. Однако это выходит за рамки данной статьи.

Искусственная нейронная сеть, с которой мы будем работать, состоит из одного входного слоя (с 784 узлами), двух скрытых слоёв (с 50 и 500 узлами соответственно) и одного выходного слоя (с 10 узлами). Мы будем повсеместно использовать сигмовидную функцию в качестве функции активации. Нейронная сеть не будет подвержена предвзятости. Обучающие данные состоят из изображений 28x28 пикселей, рукописных цифр в диапазоне от 0 до 9 из набора данных MNIST. Технически мы могли бы выбрать любой из 784*50+50*500+500*10=69,200 весов, которые мы используем в нашей нейронной сети. Я произвольно решил использовать веса w250, 5 (2) и w251,5(2), которые соединяют 250-й и 251-й узлы второго скрытого слоя с 6-м выходным нейроном соответственно. В нашей модели 6-й выходной нейрон возвращает активацию для модели, прогнозируя наличие цифры «5» на изображении. На рисунке 2 схематично показана архитектура нейронной сети, с которой мы будем работать. Из соображений ясности некоторые связи между нейронами — и большая часть весовых аннотаций — были намеренно опущены.

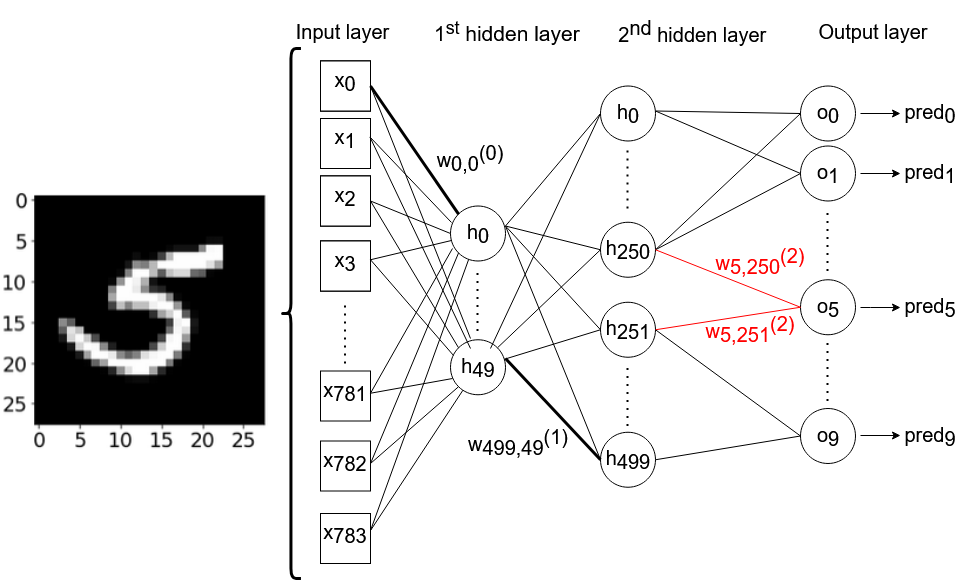
Рисунок 2 — Архитектура нейронной сети

Мы импортируем MNIST в скрипт на Python. Рукописные цифры набора данных MNIST представлены в виде изображений в оттенках серого, поэтому мы можем нормализовать входные данные путём масштабирования значений пикселей из диапазона 0-255 в диапазон 0-1,2 в нашем коде, следовательно, мы делим x-значения на 255.

# Import libraries
import numpy as np
import gzip
from sklearn.preprocessing import OneHotEncoder
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.special import expit
import celluloid
from celluloid import Camera
from matplotlib import animation 

# Open MNIST-files: 
def open_images(filename):
    with gzip.open(filename, "rb") as file:     
        data=file.read()
        return np.frombuffer(data,dtype=np.uint8, offset=16).reshape(-1,28,28).astype(np.float32) 

def open_labels(filename):
    with gzip.open(filename,"rb") as file:
        data = file.read()
        return np.frombuffer(data,dtype=np.uint8, offset=8).astype(np.float32) 
    
X_train=open_images("C:\Users\tobia\train-images-idx3-ubyte.gz").reshape(-1,784).astype(np.float32) 
X_train=X_train/255 # rescale pixel values to 0-1

y_train=open_labels("C:\Users\tobia\train-labels-idx1-ubyte.gz")
oh=OneHotEncoder(categories='auto') 
y_train_oh=oh.fit_transform(y_train.reshape(-1,1)).toarray() # one-hot-encoding of y-values

Чтобы создать ландшафты потерь, создадим график поверхности стоимости по отношению к вышеупомянутым весам w_250, 5(2) и w_251,5(2). Для этого мы определим среднеквадратичную функцию стоимости ошибки по отношению к весам w_a и w_b. Стоимости нашей модели J эквивалентны усреднённой сумме квадратичных ошибок между прогнозом модели и фактическим значением каждого из 10 выходных нейронов нашего обучающего набора данных с размером N:

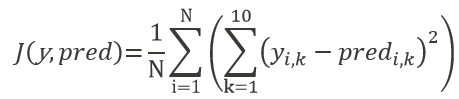
С y и pred, представляющим матрицы фактических и прогнозируемых значений y соответственно. Прогнозируемые значения вычисляются путём прямого распространения входных данных через нейронную сеть на конечный слой. Вывод каждого слоя служит входными данными для следующего слоя. Входная матрица умножается на весовую матрицу соответствующего слоя. После этого сигмоидная функция применяется для получения выходных данных этого конкретного слоя. Весовые матрицы инициализируются малыми случайными числами с помощью генератора псевдослучайных чисел numpy. С помощью seed  мы гарантируем воспроизводимость результатов. После этого подставляем два веса, которые могут изменяться в зависимости от аргументов функции w_a и w_b. Мы разработали функцию затрат на Python следующим образом:

hidden_0=50 # number of nodes of first hidden layer
hidden_1=500 # number of nodes of second hidden layer

# Set up cost function:
def costs(x,y,w_a,w_b,seed_):  
        np.random.seed(seed_) # insert random seed 
        w0=np.random.randn(hidden_0,784)  # weight matrix of 1st hidden layer
        w1=np.random.randn(hidden_1,hidden_0) # weight matrix of 2nd hidden layer
        w2=np.random.randn(10,hidden_1) # weight matrix of output layer
        w2[5][250] = w_a # set value for weight w_250,5(2)
        w2[5][251] = w_b # set value for weight w_251,5(2)
        a0 = expit(w0 @ x.T)  # output of 1st hidden layer
        a1=expit(w1 @ a0)  # output of 2nd hidden layer
        pred= expit(w2 @ a1) # output of final layer
        return np.mean(np.sum((y-pred)**2,axis=0)) # costs w.r.t. w_a and w_b

Чтобы создать графики, мы определяем диапазоны значений для наших весов и строим сетку, получая таким образом все возможные комбинации значений веса для w_a и w_b соответственно. Для каждой пары w_a и w_b в нашей сетке мы намерены рассчитать соответствующие стоимости с помощью нашей функции стоимости. Далее мы можем, наконец, создать некоторые ландшафты потерь:

# Set range of values for meshgrid: 
m1s = np.linspace(-15, 17, 40)   
m2s = np.linspace(-15, 18, 40)  
M1, M2 = np.meshgrid(m1s, m2s) # create meshgrid 

# Determine costs for each coordinate in meshgrid: 
zs_100 = np.array([costs(X_train[0:100],y_train_oh[0:100].T  
                               ,np.array([[mp1]]), np.array([[mp2]]),135)  
                       for mp1, mp2 in zip(np.ravel(M1), np.ravel(M2))])
Z_100 = zs_100.reshape(M1.shape) # z-values for N=100

zs_10000 = np.array([costs(X_train[0:10000],y_train_oh[0:10000].T  
                               ,np.array([[mp1]]), np.array([[mp2]]),135)  
                       for mp1, mp2 in zip(np.ravel(M1), np.ravel(M2))])
Z_10000 = zs_10000.reshape(M1.shape) # z-values for N=10,000


# Plot loss landscapes: 
fig = plt.figure(figsize=(10,7.5)) # create figure
ax0 = fig.add_subplot(121, projection='3d' )
ax1 = fig.add_subplot(122, projection='3d' )

fontsize_=20 # set axis label fontsize
labelsize_=12 # set tick label size

# Customize subplots: 
ax0.view_init(elev=30, azim=-20)
ax0.set_xlabel(r'$w_a$', fontsize=fontsize_, labelpad=9)
ax0.set_ylabel(r'$w_b$', fontsize=fontsize_, labelpad=-5)
ax0.set_zlabel("costs", fontsize=fontsize_, labelpad=-30)
ax0.tick_params(axis='x', pad=5, which='major', labelsize=labelsize_)
ax0.tick_params(axis='y', pad=-5, which='major', labelsize=labelsize_)
ax0.tick_params(axis='z', pad=5, which='major', labelsize=labelsize_)
ax0.set_title('N:100',y=0.85,fontsize=15) # set title of subplot 

ax1.view_init(elev=30, azim=-30)
ax1.set_xlabel(r'$w_a$', fontsize=fontsize_, labelpad=9)
ax1.set_ylabel(r'$w_b$', fontsize=fontsize_, labelpad=-5)
ax1.set_zlabel("costs", fontsize=fontsize_, labelpad=-30)
ax1.tick_params(axis='y', pad=-5, which='major', labelsize=labelsize_)
ax1.tick_params(axis='x', pad=5, which='major', labelsize=labelsize_)
ax1.tick_params(axis='z', pad=5, which='major', labelsize=labelsize_)
ax1.set_title('N:10,000',y=0.85,fontsize=15)

# Surface plots of costs (= loss landscapes):  
ax0.plot_surface(M1, M2, Z_100, cmap='terrain', #surface plot
                             antialiased=True,cstride=1,rstride=1, alpha=0.75)
ax1.plot_surface(M1, M2, Z_10000, cmap='terrain', #surface plot
                             antialiased=True,cstride=1,rstride=1, alpha=0.75)
plt.tight_layout()
plt.show()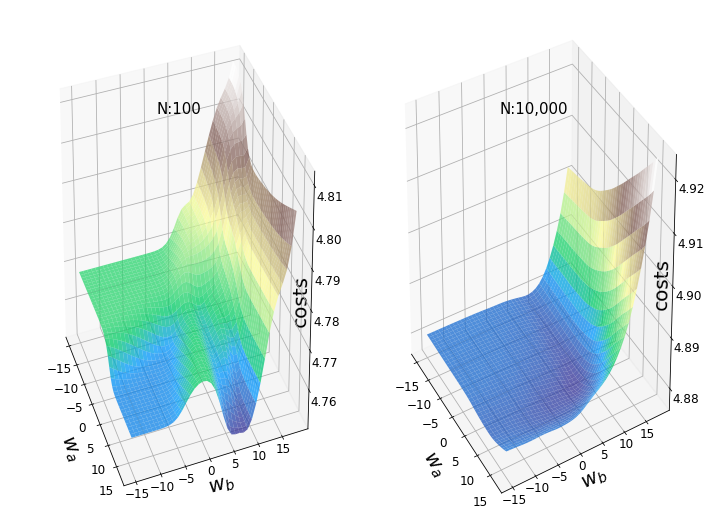

Рисунок 3 — Ландшафты с различными размерами образцов

На рисунке 3 показаны два примерных ландшафта потерь с одинаковыми весами (w_250, 5 (2) и w_251,5(2)) и одинаковыми случайными начальными весами. Левый участок поверхности создавался с помощью первых 100 изображений набора данных MNIST, в то время как участок справа был создан с помощью первых 10 000 изображений. Если мы присмотримся к левому графику, то увидим некоторые типичные черты невыпуклых ландшафтов потерь: локальные минимумы, плато, хребты (иногда также называемые «седловыми точками») и «глобальный» минимум. Однако термин «минимум» следует использовать с осторожностью, поскольку мы видим только заданный диапазон значений, вместе с тем не проводился тест первой производной.

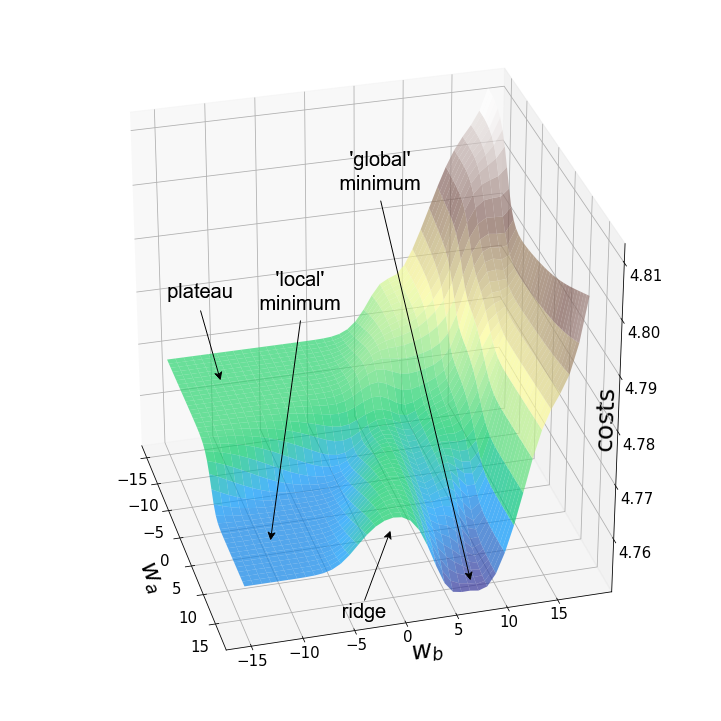
Рисунок 4

Градиентный спуск

Эти «географические барьеры» резко контрастируют с гладкими и выпуклыми ландшафтами потерь, которые можно увидеть в линейной и логистической регрессиях. Считается, что эти «барьеры» замедляют достижение глобального минимума и даже препятствуют этому, а следовательно, негативно влияют на производительность модели [3]. Для исследования явления я решил анимировать градиентный спуск с этим конкретным ландшафтом потерь и тремя характерными начальными точками. Градиентный спуск в основном компрометирует обновление параметров модели (например, весов) в соответствии со следующим уравнением:

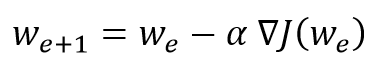
где ∇J — градиент нашей функции стоимости, w — вес всей модели, e — соответствующая эпоха и α — скорость обучения.

Поскольку оба веса в нашем примере содержатся в выходном слое нейронной сети, достаточно получить частные производные весов в последнем слое. Для этого мы применяем правило цепочки и получаем следующее:

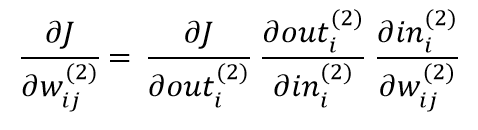
где wᵢⱼ определяется как вес между j-м узлом слоя до и i-м узлом текущего слоя, который является выходным слоем в нашем случае. Вход i-го нейрона в выходном слое просто обозначается как inᵢ (²) и эквивалентен сумме активаций слоя до умножения на их соответствующие веса соединения, ведущие к этому узлу. Выход * i*-го нейрона в выходном слое обозначается как outᵢ (²) и соответствует σ(inᵢ (²)). Решая уравнение выше, мы получаем:

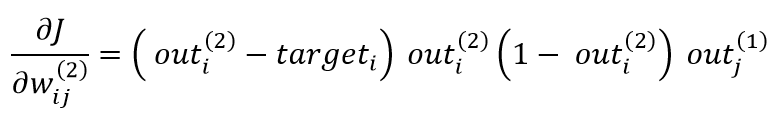
с * outⱼ (¹), соответствующим активации j-го узла в слое, перед которым в выходном слое через wᵢⱼ. соединен с n-м узлом. Переменная targetᵢ обозначает целевой вывод для каждого из 10 выходных нейронов. Ссылаясь на рисунок 2, outⱼ (¹) будет соответствовать активации h₂₅₀ или h₂₅₁, в зависимости от того веса, от которого мы намереваемся вычислить частную производную. Отличное объяснение, включая подробный математический вывод, можно найти здесь [4].

Поскольку вывод нейронов выходного слоя эквивалентен прогнозу нейронной сети, в следующем коде воспользуемся более удобной аббревиатурой 'PRE'. Поскольку строгая фокусировка на конкретном узле может привести к путанице в коде, мы стремимся придерживаться установленного принципа использования весовых матриц и умножения матриц для обновления всех весов в выходном слое сразу. Наконец, мы обновим только два конкретных веса выходного слоя, которые собираемся обновить на самом деле. На Python мы реализуем алгоритм градиентного спуска только для двух весов вот так:

# Store values of costs and weights in lists: 
weights_2_5_250=[] 
weights_2_5_251=[] 
costs=[] 

seed_= 135 # random seed
N=100 # sample size 

# Set up neural network: 
class NeuralNetwork(object):
    def __init__(self, lr=0.01):
        self.lr=lr
        np.random.seed(seed_) # set random seed
        # Intialize weight matrices: 
        self.w0=np.random.randn(hidden_0,784)  
        self.w1=np.random.randn(hidden_1,hidden_0)
        self.w2=np.random.randn(10,hidden_1)
        self.w2[5][250] = start_a # set starting value for w_a
        self.w2[5][251] = start_b # set starting value for w_b
    
    def train(self, X,y):
        a0 = expit(self.w0 @ X.T)  
        a1=expit(self.w1 @ a0)  
        pred= expit(self.w2 @ a1)
        # Partial derivatives of costs w.r.t. the weights of the output layer: 
        dw2= (pred - y.T)*pred*(1-pred)  @ a1.T / len(X)   # ... averaged over the sample size
        # Update weights: 
        self.w2[5][250]=self.w2[5][250] - self.lr * dw2[5][250] 
        self.w2[5][251]=self.w2[5][251] - self.lr * dw2[5][251] 
        costs.append(self.cost(pred,y)) # append cost values to list
    
    def cost(self, pred, y):
        return np.mean(np.sum((y.T-pred)**2,axis=0))
    
# Initial values of w_a/w_b: 
starting_points = [  (-9,15),(-10.1,15),(-11,15)] 

for j in starting_points:
    start_a,start_b=j
    model=NeuralNetwork(10) # set learning rate to 10
    for i in range(10000):  # 10,000 epochs            
        model.train(X_train[0:N], y_train_oh[0:N]) 
        weights_2_5_250.append(model.w2[5][250]) # append weight values to list
        weights_2_5_251.append(model.w2[5][251]) # append weight values to list

# Create sublists of costs and weight values for each starting point: 
costs = np.split(np.array(costs),3) 
weights_2_5_250 = np.split(np.array(weights_2_5_250),3)
weights_2_5_251 = np.split(np.array(weights_2_5_251),3)

Поскольку мы обновляем только два из тысяч весов, содержащихся в модели, то при каждой итерации стоимость снижается незначительно, несмотря на относительно высокую скорость обучения α=10. Поэтому веса, которые мы собираемся обновлять, также сильно меняются, в отличие от лишь незначительных корректировок значений веса при обновлении всех моделей. Теперь мы можем анимировать три траектории градиентного спуска по отношению к трём разным стартовым точкам:

fig = plt.figure(figsize=(10,10)) # create figure
ax = fig.add_subplot(111,projection='3d' ) 
line_style=["dashed", "dashdot", "dotted"] #linestyles
fontsize_=27 # set axis label fontsize
labelsize_=17 # set tick label fontsize
ax.view_init(elev=30, azim=-10)
ax.set_xlabel(r'$w_a$', fontsize=fontsize_, labelpad=17)
ax.set_ylabel(r'$w_b$', fontsize=fontsize_, labelpad=5)
ax.set_zlabel("costs", fontsize=fontsize_, labelpad=-35)
ax.tick_params(axis='x', pad=12, which='major', labelsize=labelsize_)
ax.tick_params(axis='y', pad=0, which='major', labelsize=labelsize_)
ax.tick_params(axis='z', pad=8, which='major', labelsize=labelsize_)
ax.set_zlim(4.75,4.802) # set range for z-values in the plot

# Define which epochs to plot:
p1=list(np.arange(0,200,20))
p2=list(np.arange(200,9000,100))
points_=p1+p2

camera=Camera(fig) # create Camera object
for i in points_:
    # Plot the three trajectories of gradient descent...
    #... each starting from its respective starting point
    #... and each with a unique linestyle:
    for j in range(3): 
        ax.plot(weights_2_5_250[j][0:i],weights_2_5_251[j][0:i],costs[j][0:i],
                linestyle=line_style[j],linewidth=2,
                color="black", label=str(i))
        ax.scatter(weights_2_5_250[j][i],weights_2_5_251[j][i],costs[j][i],
                   marker='o', s=15**2,
               color="black", alpha=1.0)
    # Surface plot (= loss landscape):
    ax.plot_surface(M1, M2, Z_100, cmap='terrain', 
                             antialiased=True,cstride=1,rstride=1, alpha=0.75)
    ax.legend([f'epochs: {i}'], loc=(0.25, 0.8),fontsize=17) # set position of legend
    plt.tight_layout() 
    camera.snap() # take snapshot after each iteration
    
animation = camera.animate(interval = 5, # set delay between frames in milliseconds
                          repeat = False,
                          repeat_delay = 0)
animation.save('gd_1.gif', writer = 'imagemagick', dpi=100)  # save animation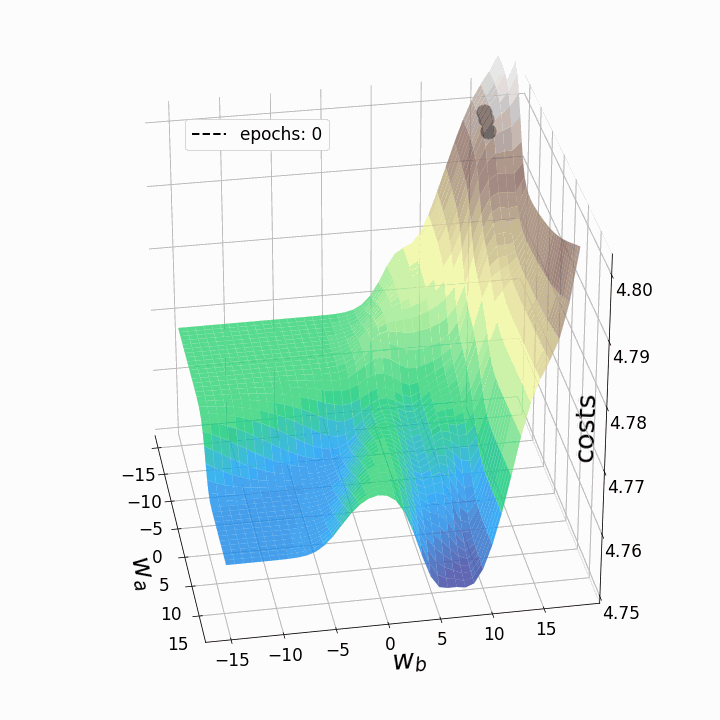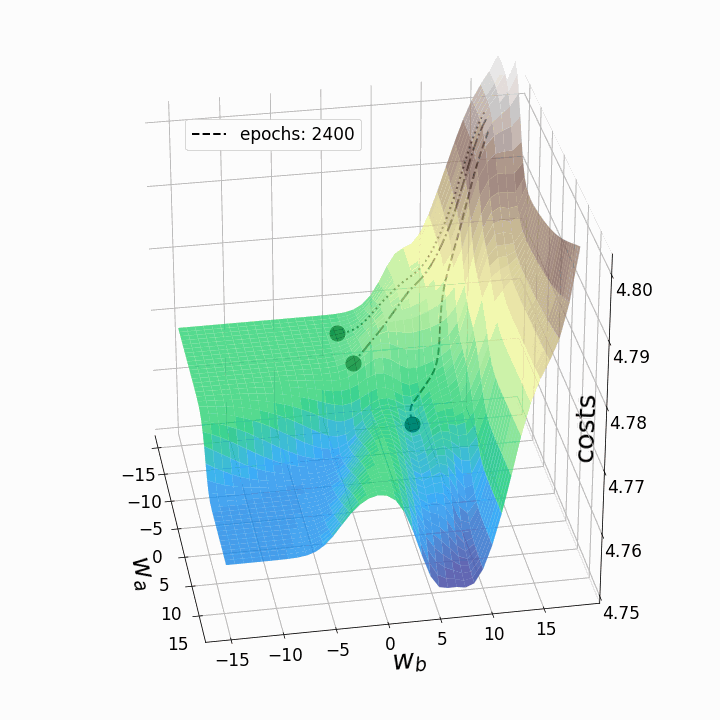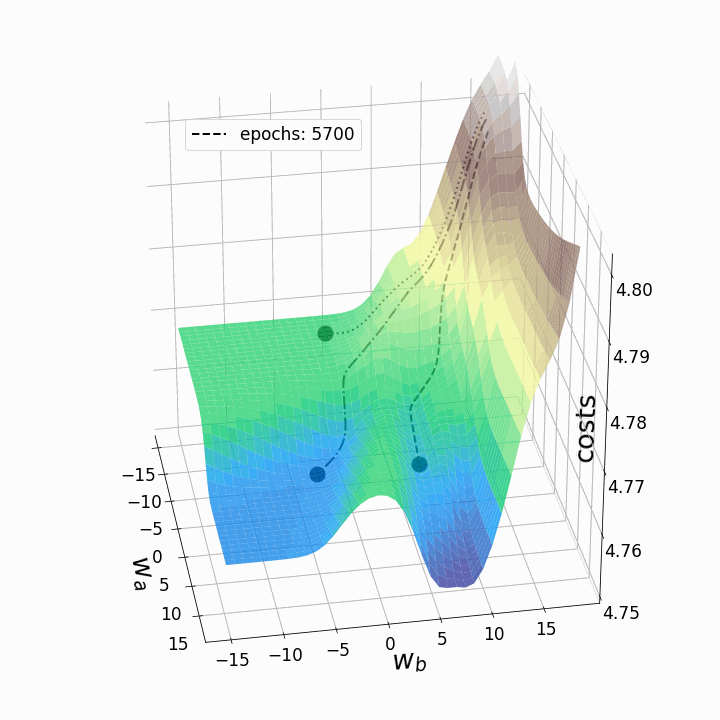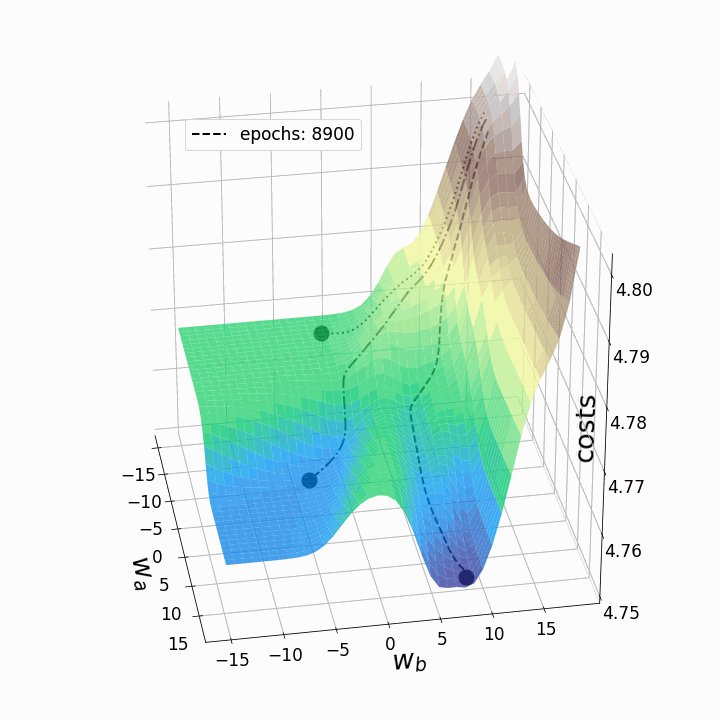   

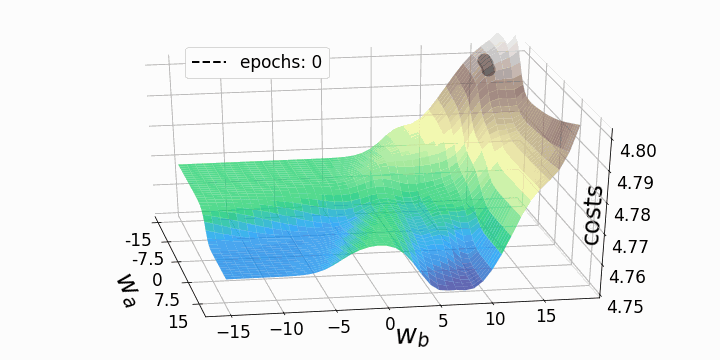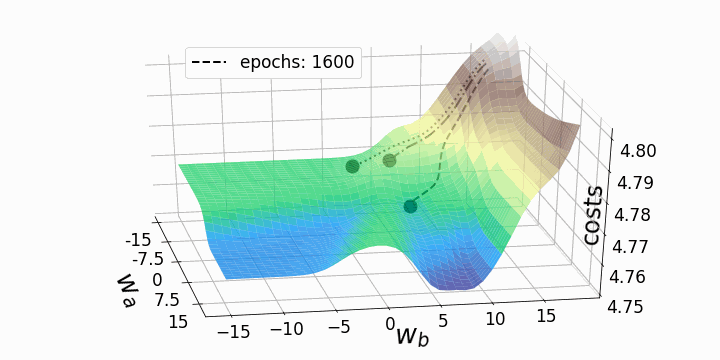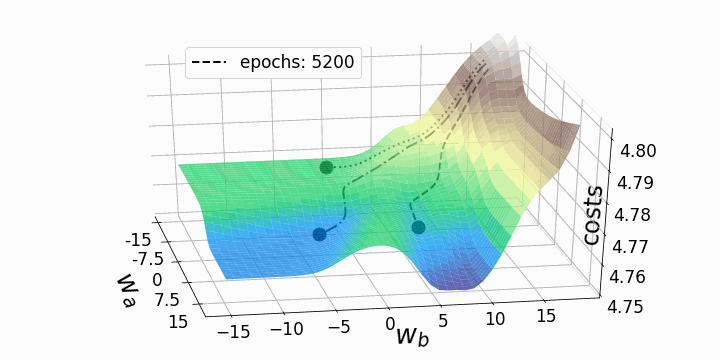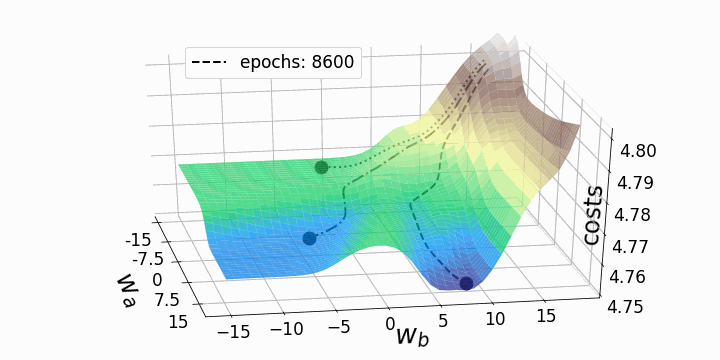
Рисунок 5 — Траектории градиентного спуска

Как и ожидалось, несогласованность ландшафтов потерь нейронных сетей делает возможным тот факт, что в зависимости от исходных значений для двух рассматриваемых нами весов градиентный спуск принимает различные маршруты в пределах ландшафта потерь. Это идёт рука об руку с разной стоимостью после определённого количества эпох и, следовательно, с разными показателями модели. Контурный график предлагает ещё одну перспективу:

fig = plt.figure(figsize=(10,10)) # create figure
ax0=fig.add_subplot(2, 1, 1) 
ax1=fig.add_subplot(2, 1, 2) 

# Customize subplots: 
ax0.set_xlabel(r'$w_a$', fontsize=25, labelpad=0)
ax0.set_ylabel(r'$w_b$', fontsize=25, labelpad=-20)
ax0.tick_params(axis='both', which='major', labelsize=17)
ax1.set_xlabel("epochs", fontsize=22, labelpad=5)
ax1.set_ylabel("costs", fontsize=25, labelpad=7)
ax1.tick_params(axis='both', which='major', labelsize=17)

contours_=21 # set the number of contour lines
points_=np.arange(0,9000,100) # define which epochs to plot

camera = Camera(fig) # create Camera object
for i in points_:
    cf=ax0.contour(M1, M2, Z_100,contours_, colors='black', # contour plot
                     linestyles='dashed', linewidths=1)
    ax0.contourf(M1, M2, Z_100, alpha=0.85,cmap='terrain') # filled contour plots 
    
    for j in range(3):
        ax0.scatter(weights_2_5_250[j][i],weights_2_5_251[j][i],marker='o', s=13**2,
               color="black", alpha=1.0)
        ax0.plot(weights_2_5_250[j][0:i],weights_2_5_251[j][0:i],
                linestyle=line_style[j],linewidth=2,
                color="black", label=str(i))
        
        ax1.plot(costs[j][0:i], color="black", linestyle=line_style[j])
    plt.tight_layout()
    camera.snap()
    
animation = camera.animate(interval = 5,
                          repeat = True, repeat_delay = 0)  # create animation 
animation.save('gd_2.gif', writer = 'imagemagick')  # save animation as gif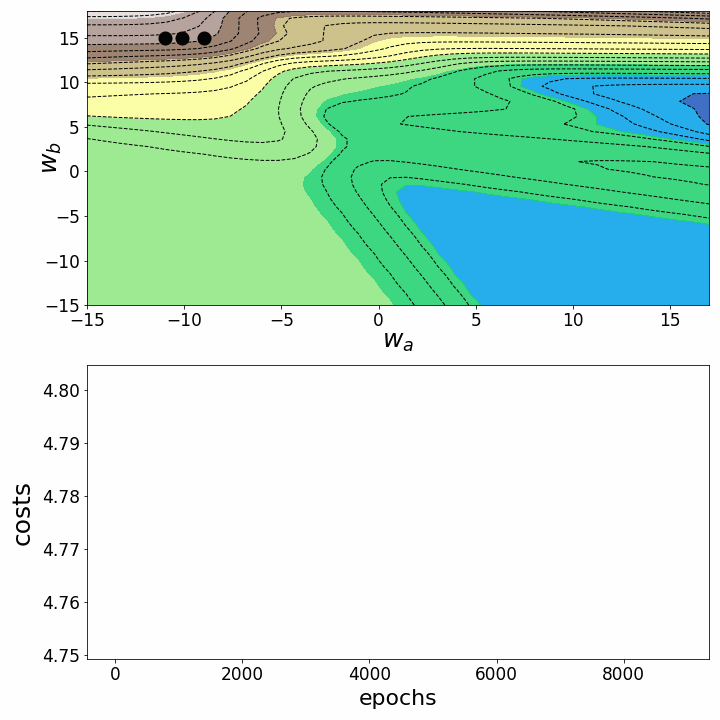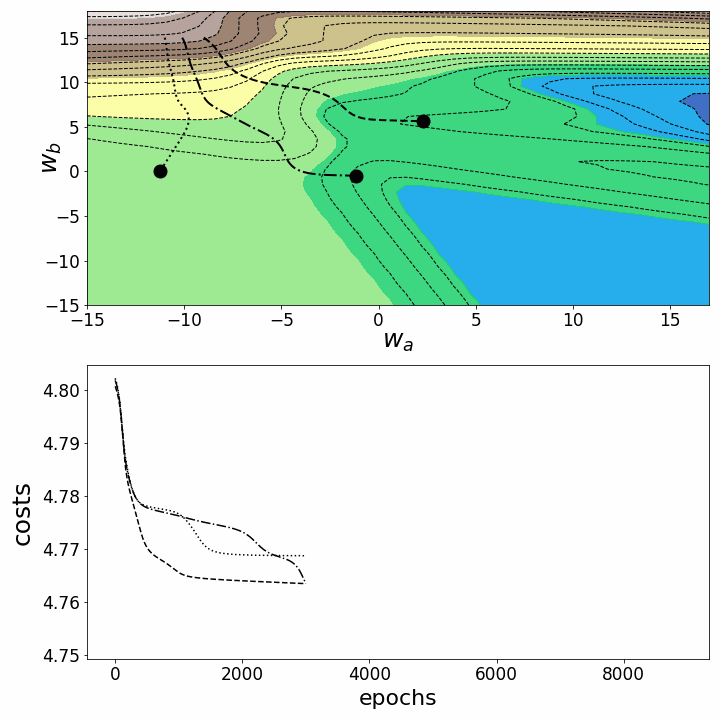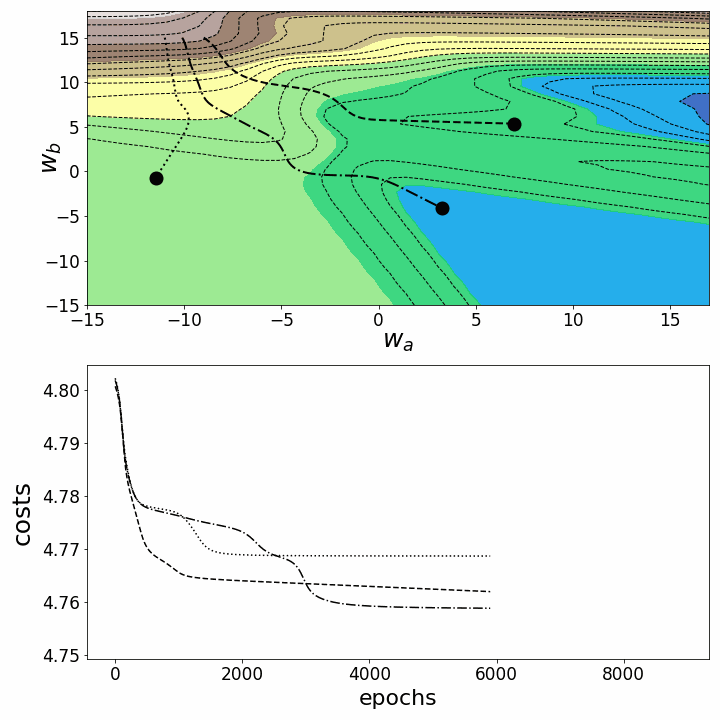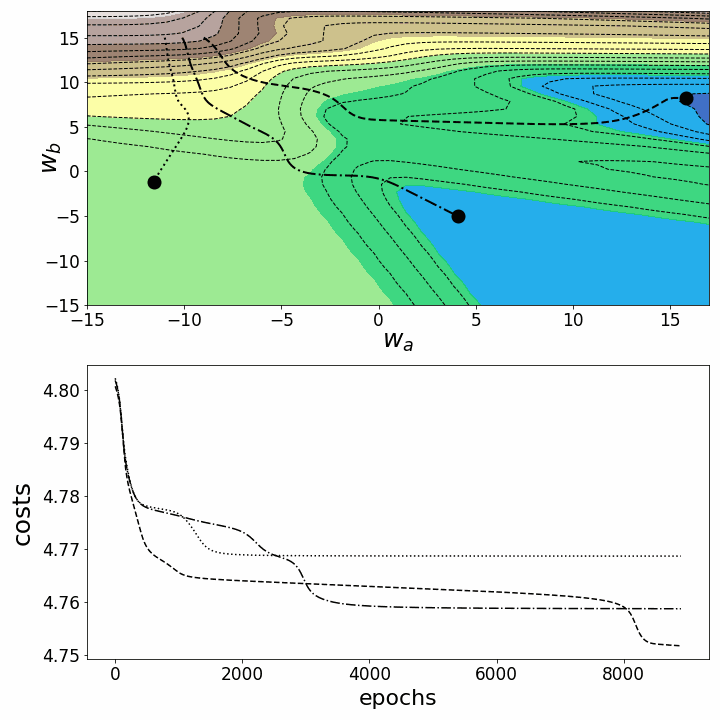

Рисунок 6 — Траектории градиентного спуска в 2D

Обе анимации показывают, что градиентный спуск может застревать в локальных минимумах, седловых точках или плато с невыпуклыми ландшафтами потерь. Для преодоления некоторых из этих препятствий были реализованы многочисленные варианты градиентного спуска (ADAGRAD, Adam и др.)⁵. Однако я хотел бы прояснить, что не все ландшафты потерь настолько невыпуклые в определённом диапазоне значений для w_a и w_b. Выпуклость ландшафта потерь зависит, среди прочего, от количества скрытых слоев, при этом глубокие нейронные сети приводят к сильно невыпуклым ландшафтам потерь¹.

Я решил создать несколько произвольных ландшафтов потерь, перебирая случайные начальные значения для генерации. На этот раз веса, которые могут изменяться, находятся на втором скрытом уровне (код). Репрезентативный образец ландшафтов потерь, с которыми я столкнулся при таком подходе, можно увидеть ниже. Размер выборки и индексы весов, представленных w_a и w_b, указаны соответственно в заголовках.

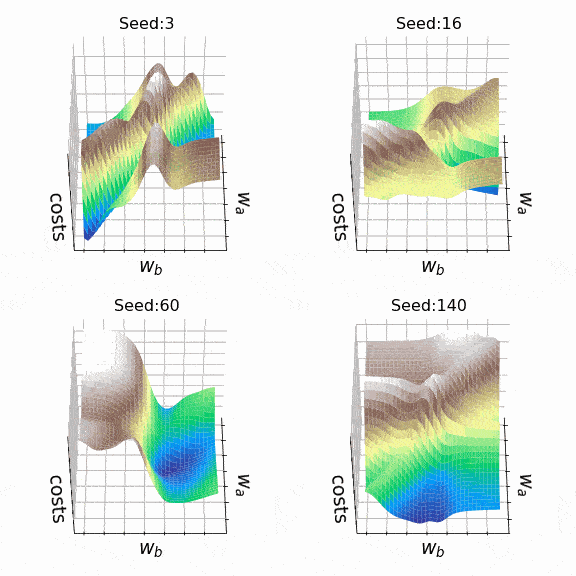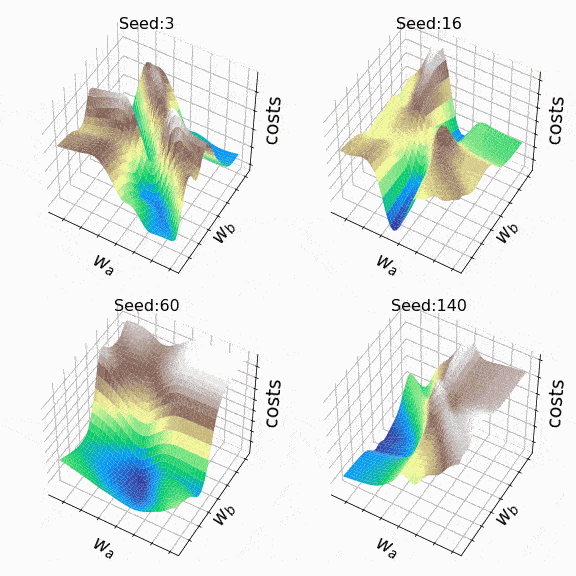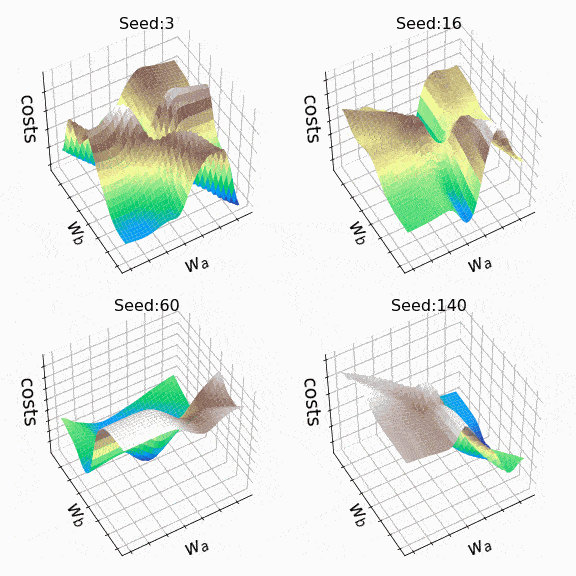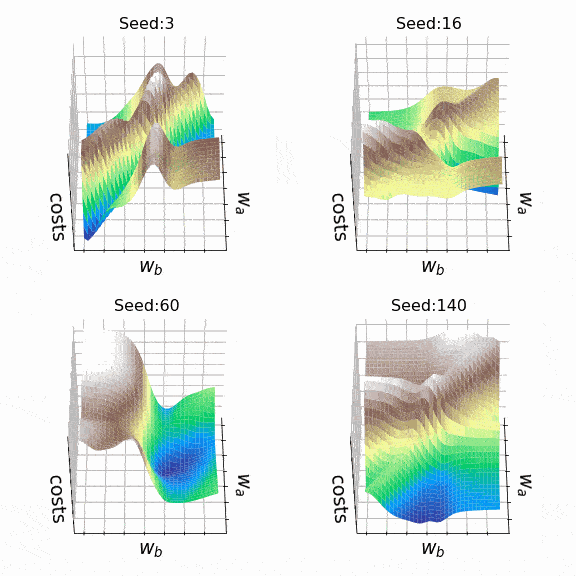
Рисунок 7 — N=500, w200–30(1), w200–31(1) (создано автором, код)

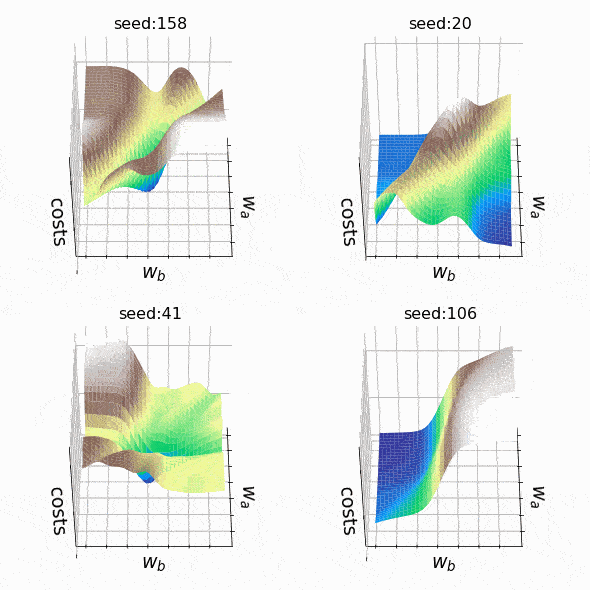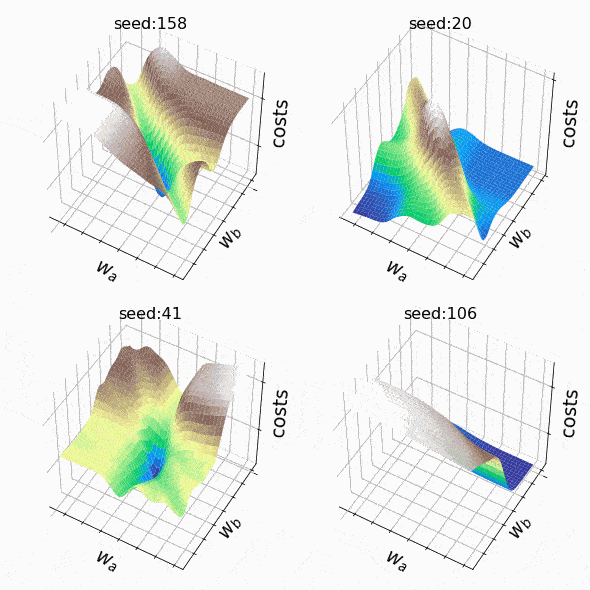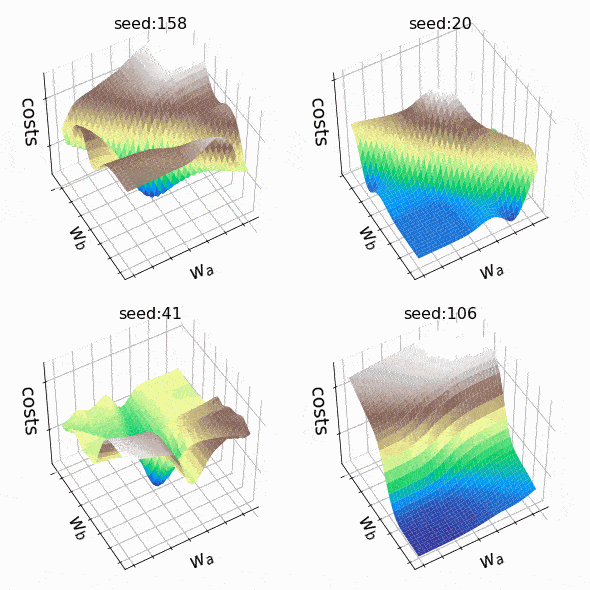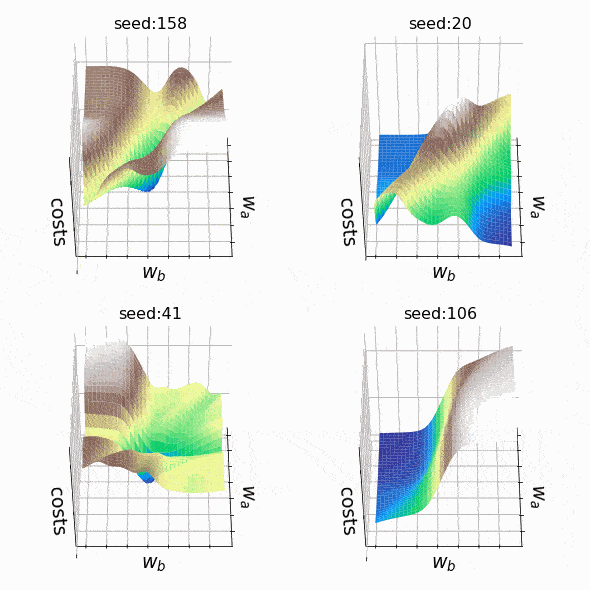
Рисунок 8 — N=1000, w5–5(1), w5–6(1) (создано автором, код)

Визуализация ландшафта потерь может быть полезна для лучшего понимания лежащей в основе теории и потенциальных недостатков различных алгоритмов оптимизации. Однако на практике актуальность локальных минимумов, плато или хребтов всё ещё обсуждается. Некоторые авторы утверждают, что локальные минимумы очень редки в многомерных пространствах и что седловые точки могут быть даже более проблематичными, чем локальные минимумы в отношении оптимизации параметров. Другие авторы даже предполагают, что минимизация затрат, связанная с локальными минимумами, является достаточной и может предотвратить переобучение [7].

Я надеюсь, что вам понравилось! Полный код Jupyter Notebook можно найти на моём GitHub.

Приложение

Представленное изображение

• Обучение профессии Data Science
• Обучение профессии Data Analyst

Автор: one-two

Источник