Фильтр Калмана (ФК) является оптимальным линейным алгоритмом фильтрации параметров динамической линейной системы при наличии неполных и зашумленных наблюдений. Этот фильтр находит широкое применение в технических системах управления до оценок динамики изменения макроэкономических ситуаций или общественного мнения.
Данная статья ставит себе целью познакомить читателя со стандартным подходом к переходу от непрерывной модели динамической системы, описываемой системой произвольных линейных дифференциальных уравнений к дискретной модели.
Так же эта статья призвана сподвигнуть читателя на применение ФК в тех задачах, где на первый взгляд кажется что линейный ФК неприменим, а на самом деле это может быть не так.
Написать статью автора сподвиг тот факт, что несмотря на простоту последующих вещей в поисковой выдаче гугла как на русском так и на английском языке (по крайней мере на первой странице) автору найти их не удалось.
Динамическая модель для дискретного фильтра Калмана
ФК может быть выполнен как в дискретном так и непрерывном виде. Наибольший интерес с точки зрения практической реализации на современных цифровых вычислителях представляет именно дискретный ФК на который будет сделан упор в данной статье.
Линейный дискретный ФК описывается следующими выражениями. Пусть модель системы может быть представлена следующим образом:
$$display$$mathbf{x}_{k} = F mathbf{x}_{k-1} + Psi mathbf{u}_k + Gamma mathbf{w}_k$$display$$
где $inline$F$inline$ — матрица перехода, $inline$Psi$inline$ — переходная матрица управления, $inline$Gamma$inline$ — переходная матрица возмущения, $inline$mathbf{x}_k$inline$, $inline$mathbf{u}_k$inline$, $inline$mathbf{w}_k$inline$ — вектора состояния, управления и шумов (возмущения) системы на $inline$k$inline$-том шаге. Модель наблюдения:
$$display$$mathbf{z}_k = Hmathbf{x}_k + mathbf{n}_k$$display$$
где $inline$mathbf{z}_k$inline$, $inline$mathbf{n}_k$inline$ — вектора наблюдения и шума наблюдения на $inline$k$inline$-том шаге. 5 уравнений работы ФК в данной статье интереса не представляют, поэтому на случай если они кому-либо нужны приводятся под спойлером.
$$display$$ mathbf{x}_{k|k-1} = F hat{mathbf{x}}_{k-1} + mathbf{w}_k$$display$$
$$display$$ P_{k|k-1} = FP_{k-1}F^T + Q_k$$display$$
Данный этап принято называть экстраполяцией. Следующий этап, называемый коррекция:
$$display$$ K = PH^T(HP_{k|k-1}H^T + R)^{-1}$$display$$
собственно самой оценки
$$display$$ hat{mathbf{x}}_{k} = x_{k|k-1} + K(Hmathbf{z}_k-mathbf{x}_{k|k-1})$$display$$
$$display$$ P_k = (E-KH)P_{k|k-1}$$display$$
Здесь и далее речь идет о стационарных (с постоянными коэффициентами) системах, для которых матрицы $inline$F$inline$, $inline$Psi$inline$ и $inline$Gamma$inline$ не зависят от номера $inline$k$inline$.
Непрерывная динамическая модель системы. Пространство состояний.
В подавляющем большинстве практических приложений ФК осуществляет фильтрацию параметров непрерывных динамических систем, описываемых дифференциальными уравнениями для непрерывного времени. Обсчет ФК при этом происходит на цифровом вычислителе, что автоматически делает ФК дискретным и модель соответственно должна быть дискретной. Для получения дискретной модели этих непрерывных систем необходимо сначала составить сам вектор состояния (фазовый вектор), систему уравнения состояния, затем дискретизировать их, получив тем самым матрицы $inline$F$inline$, $inline$Psi$inline$ и $inline$Gamma$inline$.
Пусть поведение системы описывается набором из $inline$n$inline$ дифференциальных уравнений первого порядка:
$$display$$ dot{mathbf{x}}(t) = Amathbf{x}(t) + Bmathbf{u}(t) + Gmathbf{w}(t) $$display$$
здесь $inline$mathbf{x}$inline$ — $inline$n$inline$-мерный вектор состояния системы. Вектор состояния (он же фазовый вектор) это вектор, который содержит в себе переменные, описывающие систему и их производные вплоть до необходимого порядка. $inline$mathbf{u}$inline$ — $inline$r$inline$-мерный вектор управления системы, описывающий оказываемое на систему контролируемое воздействие.
$inline$mathbf{w}$inline$ $inline$p$inline$-мерный вектор, содержащий в себе случайное неконтролируемое воздействие на систему, или шумы. $inline$A$inline$ — матрица состояния системы размером $inline$n times n$inline$. $inline$B$inline$ — матрица управления размером $inline$n times r$inline$. $inline$G$inline$ — матрица возмущения размером $inline$n times p$inline$. В этом выражении все произведения вычисляются по правилам матричного умножения. В общем случае элементы всех матриц являются функциями времени, однако в статье рассматриваются только стационарные системы, где элементы не зависят от времени.
Пример перехода от описания системы с помощью дифференциального уравнения высшего порядка к описанию через пространство состояний приведен ниже.
$$display$$ ddot{x} = -omega^2 x $$display$$
Если кто не помнит, таким образом представляется колебательное движение. Перейдем от уравнения второго порядка к системе из двух уравнений путем введения новой переменной $inline$x_1 = dot{x}$inline$. Теперь имеем:
$$display$$ begin{aligned} dot{x} &= x_1 \ dot{x}_1 &= -omega^2 x end{aligned}$$display$$
Данная система уравнений может быть записана в матричном виде, при этом вектор состояния $inline$mathbf{x} = [x , x_1]^T$inline$, матрица состояния окажется
$$display$$ A = begin{bmatrix} 0 & 1 \ -omega^2 & 0 end{bmatrix} $$display$$
Введенная переменная $inline$x_1$inline$ играет роль скорости. Матрицы $inline$B$inline$ и $inline$G$inline$ в данном примере являются нулевыми, так как отсутствуют какие-либо управляющие и возмущающие воздействия.
Переход в дискретную область
Для корректного перехода в дискретную область (другими словами дискретизации модели) нам потребуется ввести понятие матричной экспоненты. Матричной экспонентой называется матричная функция, полученная по аналогии с разложением экспоненциальной функции в ряд Тейлора на самом деле Маклорена:
$$display$$e^{At} = E + At + , ... , dfrac{A^nt^n}{n!} + , ... , = sum_{k=0}^{infty} dfrac{A^nt^n}{n!}$$display$$
где под $inline$E$inline$ подразумевается единичная матрица.
Точный переход от непрерывной модели в пространстве состояний к дискретной модели требует поиска решения однородной системы $inline$ dot{mathbf{x}}(t) = A(t)mathbf{x}(t) $inline$, затем перехода к первоначальной системе, отыскания общего решения и интегрирования от начального момента $inline$ t_0 $inline$ до некоторого $inline$ t $inline$. Строгий вывод может быть найден в [1], здесь же приводится готовый результат.
В случае стационарности непрерывной динамической модели (не зависимости матриц $inline$A$inline$, $inline$B$inline$, $inline$G$inline$ от времени) для получения дискретной модели можно ввести вспомогательную переходную матрицу системы $inline$Phi(t, tau)$inline$ из момента $inline$tau$inline$ в момент $inline$t$inline$, где $inline$t > tau$inline$:
$$display$$ Phi(t, tau) = e^{A(t-tau)} = sum_{k=0}^{infty} dfrac{A^nt^n}{n!} $$display$$
Далее с помощью этой вспомогательной матрицы могут быть получены требуемые для дискретной модели матрицы:
$$display$$F = Phi(t + T, t) = e^{AT} = E + AT + dfrac{A^2T^2}{2!} + dfrac{A^3T^3}{3!} + ... $$display$$
$$display$$ Gamma = int_{kT}^{(k+1)T}Phi(t_{k+1},tau)G(tau) dtau $$display$$
$$display$$ Psi = int_{kT}^{(k+1)T}Phi(t_{k+1},tau)B(tau) dtau$$display$$
Здесь под $inline$B(tau)$inline$ и $inline$G(tau)$inline$ подразумеваются матрицы из непрерывных уравнений, под $inline$Psi$inline$ и $inline$Gamma$inline$ искомые матрицы дискретной модели.
Практические примеры
Для иллюстрации вышеописанной математики рассмотрим два примера. Один из которых разминочный, а второй иллюстративный, для демонстрации возможностей описанного метода.
Тривиальный
Пусть объект движется вдоль оси $inline$Ox$inline$ с начальной скоростью $inline$v_0$inline$ и постоянным ускорением $inline$a$inline$. Тогда его модель может быть представлена в виде:
$$display$$ddot{x} = a$$display$$
Представим эту модель в виде системы однородных дифференциальных уравнений. Для этого разобьем уравнение на систему из трех ДУ:
$$display$$begin{aligned} dot{x} &= v_x \ dot{v}_x &= a_x \ dot{a}_x &= 0 end{aligned}$$display$$
При записи систем уравнений туда добавляются следующие производные пока для вычисления текущей требуется следующая. То в текущей системе нельзя остановиться на $inline$v_x$inline$, так как для вычисления требуется $inline$a_x$inline$. В то же время для вычисления $inline$a_x$inline$ производная $inline$dot{a}_x$inline$ не требуется, поэтому вносить производные порядка выше $inline$a_x$inline$ в вектор состояния не имеет особого смысла.
Объединим три переменных в вектор состояния $inline$mathbf{x} = [x , v_x , a_x]^T$inline$ и запишем систему уравнений в матричном виде для перехода к форме пространства состояния:
$$display$$dot{mathbf{x}} = Amathbf{x}$$display$$
где матрица
$$display$$A = begin{bmatrix} 0 & 1 & 0 \ 0 & 0 & 1 \ 0 & 0 & 0 end{bmatrix}$$display$$
Теперь можно рассчитать матрицу перехода дискретной динамической системы, соответствующей рассматриваемой непрерывной:
$inline$begin{aligned} F = E + Acdot T + A times Acdotdfrac{T^2}{2} = begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end{bmatrix} + begin{bmatrix} 0 & 1 & 0 \ 0 & 0 & 1 \ 0 & 0 & 0 end{bmatrix}cdot T + \ begin{bmatrix} 0 & 0 & 1 \ 0 & 0 & 0 \ 0 & 0 & 0 end{bmatrix} cdotdfrac{T^2}{2} = begin{bmatrix} 1 & T & T^2/2 \ 0 & 1 & T \ 0 & 0 & 1 end{bmatrix} end{aligned}$inline$
Читатель может сам убедиться в том, что $inline$A^3$inline$ и выше представляет собой нулевую матрицу.
Таким образом получена известная всем матрица перехода, выведенная без применения каких-либо допущений.
Нетривиальный пример
Положим что наш объект движется в трехмерном пространстве с некой постоянной (по модулю) линейной скоростью и с угловой скоростью, представленной псевдовектором:
$$display$$omega = [omega_x, omega_y,omega_z]^T$$display$$
Для начала необходимо составить уравнения пространства состояний. Запишем ускорение при движении по окружности. Из курса физики за 1 семестр известно, что центростремительное ускорение является векторным произведением угловой и линейной скоростей:
$$display$$ dot{v} = omega times v$$display$$
Здесь вектор скорости представляет собой $inline$v = [v_x,v_y,v_z]^T$inline$.
Распишем векторное произведение подробнее:
$$display$$omega times v = begin{bmatrix} omega_x \ omega_y \ omega_z end{bmatrix} times begin{bmatrix} v_x \ v_y \ v_z end{bmatrix} = begin{bmatrix} omega_yz-omega_zy \ omega_zx-omega_xz \ omega_xy-omega_yx end{bmatrix}$$display$$
Теперь запишем систему уравнений
$$display$$begin{aligned} dot{x} &= v_x \ dot{y} &= v_y \ dot{z} &= v_z \ dot{v}_x &= omega_yz-omega_zy \ dot{v}_y &= omega_zx-omega_xz \ dot{v}_z &= omega_xy-omega_yx end{aligned} $$display$$
При переходе к матричной форме матрица $inline$A$inline$ будет представлять собой:
$$display$$A = begin{bmatrix} 0 & 0 & 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 & 0 & 1 \ 0 & 0 & 0 & 0 & -omega_z & omega_y \ 0 & 0 & 0 & omega_z & 0 & -omega_x \ 0 & 0 & 0 & -omega_y & omega_x & 0 end{bmatrix}$$display$$
Далее осуществим переход к матрице $inline$F$inline$ по соответствующему выражению. Так как устно перемножать матрицы размером $inline$6 times 6 $inline$ по три раза довольно тяжело, вероятность ошибки велика, да и не царское это дело, то напишем скрипт с использованием библиотеки sympy языка Python:
from sympy import symbols, Matrix, eye
x, y, z, T = symbols('x y z T')
vx, vy, vz = symbols('v_x v_y v_z')
wx, wy, wz = symbols('w_x w_y w_z')
A = Matrix([
[0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, -wz, wy],
[0, 0, 0, wz, 0, -wx],
[0, 0, 0, -wy, wx, 0]
])
F = eye(6) + A*T + A*A*T**2/2
from sympy import latex
print(latex(F))
И запустив его получим примерно вот это:
left[begin{matrix}1 & 0 & 0 & T & - frac{T^{2} w_{z}}{2} & frac{T^{2} w_{y}}{2}\0 & 1 & 0 & frac{T^{2} w_{z}}{2} & T & - frac{T^{2} w_{x}}{2}\0 & 0 & 1 & - frac{T^{2} w_{y}}{2} & frac{T^{2} w_{x}}{2} & T\0 & 0 & 0 & frac{T^{2} left(- w_{y}^{2} - w_{z}^{2}right)}{2} + 1 & frac{T^{2} w_{x} w_{y}}{2} - T w_{z} & frac{T^{2} w_{x} w_{z}}{2} + T w_{y}\0 & 0 & 0 & frac{T^{2} w_{x} w_{y}}{2} + T w_{z} & frac{T^{2} left(- w_{x}^{2} - w_{z}^{2}right)}{2} + 1 & frac{T^{2} w_{y} w_{z}}{2} - T w_{x}\0 & 0 & 0 & frac{T^{2} w_{x} w_{z}}{2} - T w_{y} & frac{T^{2} w_{y} w_{z}}{2} + T w_{x} & frac{T^{2} left(- w_{x}^{2} - w_{y}^{2}right)}{2} + 1end{matrix}right]
Что после обрамления соответствующими тэгами и вставки в исходный код статьи превращается в:
$$display$$ F = left[begin{matrix}1 & 0 & 0 & T & - frac{T^{2} w_{z}}{2} & frac{T^{2} w_{y}}{2}\0 & 1 & 0 & frac{T^{2} w_{z}}{2} & T & - frac{T^{2} w_{x}}{2}\0 & 0 & 1 & - frac{T^{2} w_{y}}{2} & frac{T^{2} w_{x}}{2} & T\0 & 0 & 0 & frac{T^{2} left(- w_{y}^{2} - w_{z}^{2}right)}{2} + 1 & frac{T^{2} w_{x} w_{y}}{2} - T w_{z} & frac{T^{2} w_{x} w_{z}}{2} + T w_{y}\0 & 0 & 0 & frac{T^{2} w_{x} w_{y}}{2} + T w_{z} & frac{T^{2} left(- w_{x}^{2} - w_{z}^{2}right)}{2} + 1 & frac{T^{2} w_{y} w_{z}}{2} - T w_{x}\0 & 0 & 0 & frac{T^{2} w_{x} w_{z}}{2} - T w_{y} & frac{T^{2} w_{y} w_{z}}{2} + T w_{x} & frac{T^{2} left(- w_{x}^{2} - w_{y}^{2}right)}{2} + 1end{matrix}right] $$display$$
Таким образом может быть выведена матрица перехода фильтра Калмана для движения по окружности.
В отличии от предыдущего случая результат возведения $inline$A$inline$ в степень выше 3 не является нулевой матрицей.
$$display$$left[begin{matrix}0 & 0 & 0 & - w_{y}^{2} - w_{z}^{2} & w_{x} w_{y} & w_{x} w_{z}\0 & 0 & 0 & w_{x} w_{y} & - w_{x}^{2} - w_{z}^{2} & w_{y} w_{z}\0 & 0 & 0 & w_{x} w_{z} & w_{y} w_{z} & - w_{x}^{2} - w_{y}^{2}\0 & 0 & 0 & 0 & w_{x}^{2} w_{z} - w_{z} left(- w_{y}^{2} - w_{z}^{2}right) & - w_{x}^{2} w_{y} + w_{y} left(- w_{y}^{2} - w_{z}^{2}right)\0 & 0 & 0 & - w_{y}^{2} w_{z} + w_{z} left(- w_{x}^{2} - w_{z}^{2}right) & 0 & w_{x} w_{y}^{2} - w_{x} left(- w_{x}^{2} - w_{z}^{2}right)\0 & 0 & 0 & w_{y} w_{z}^{2} - w_{y} left(- w_{x}^{2} - w_{y}^{2}right) & - w_{x} w_{z}^{2} + w_{x} left(- w_{x}^{2} - w_{y}^{2}right) & 0end{matrix}right]$$display$$
$$display$$left[begin{matrix}0 & 0 & 0 & 0 & w_{x}^{2} w_{z} - w_{z} left(- w_{y}^{2} - w_{z}^{2}right) & - w_{x}^{2} w_{y} + w_{y} left(- w_{y}^{2} - w_{z}^{2}right)\0 & 0 & 0 & - w_{y}^{2} w_{z} + w_{z} left(- w_{x}^{2} - w_{z}^{2}right) & 0 & w_{x} w_{y}^{2} - w_{x} left(- w_{x}^{2} - w_{z}^{2}right)\0 & 0 & 0 & w_{y} w_{z}^{2} - w_{y} left(- w_{x}^{2} - w_{y}^{2}right) & - w_{x} w_{z}^{2} + w_{x} left(- w_{x}^{2} - w_{y}^{2}right) & 0\0 & 0 & 0 & - w_{y} left(- w_{x}^{2} w_{y} + w_{y} left(- w_{y}^{2} - w_{z}^{2}right)right) + w_{z} left(w_{x}^{2} w_{z} - w_{z} left(- w_{y}^{2} - w_{z}^{2}right)right) & w_{x} left(- w_{x}^{2} w_{y} + w_{y} left(- w_{y}^{2} - w_{z}^{2}right)right) & - w_{x} left(w_{x}^{2} w_{z} - w_{z} left(- w_{y}^{2} - w_{z}^{2}right)right)\0 & 0 & 0 & - w_{y} left(w_{x} w_{y}^{2} - w_{x} left(- w_{x}^{2} - w_{z}^{2}right)right) & w_{x} left(w_{x} w_{y}^{2} - w_{x} left(- w_{x}^{2} - w_{z}^{2}right)right) - w_{z} left(- w_{y}^{2} w_{z} + w_{z} left(- w_{x}^{2} - w_{z}^{2}right)right) & w_{y} left(- w_{y}^{2} w_{z} + w_{z} left(- w_{x}^{2} - w_{z}^{2}right)right)\0 & 0 & 0 & w_{z} left(- w_{x} w_{z}^{2} + w_{x} left(- w_{x}^{2} - w_{y}^{2}right)right) & - w_{z} left(w_{y} w_{z}^{2} - w_{y} left(- w_{x}^{2} - w_{y}^{2}right)right) & - w_{x} left(- w_{x} w_{z}^{2} + w_{x} left(- w_{x}^{2} - w_{y}^{2}right)right) + w_{y} left(w_{y} w_{z}^{2} - w_{y} left(- w_{x}^{2} - w_{y}^{2}right)right)end{matrix}right]$$display$$
Поэтому представление такой матрицы возможно с конечной точностью. Однако при $inline$ omega T ll 1 $inline$ ряды, получающиеся в элементах матрицы $inline$F$inline$ сходятся довольно быстро. Для практического применения достаточно членов до второй степени, редко до третьей и тем более до четвертой.
Дополнительно проиллюстрируем работу матрицы $inline$ F $inline$ задав вектор $inline$ omega $inline$, $inline$ bf{x}_0 $inline$, $inline$ bf{v}_0 $inline$, и рекуррентную последовательность вида:
$$display$$mathbf{x}_k = Fmathbf{x}_{k-1}$$display$$
Рассчитаем данную рекуррентную последовательность для $inline$ omega T approx frac{1}{100} $inline$
import numpy as np
from numpy import pi
T = 1
wx, wy, wz = 0, 2*pi/100/2**.5, 2*pi/100/2**.5
vx0 = 10
A = np.array([
[0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, -wz, wy],
[0, 0, 0, wz, 0, -wx],
[0, 0, 0, -wy, wx, 0]
])
F = np.eye(6) + A * T + A @ A * T**2/2 + A @ A @ A * T**3/6
X = np.zeros((6, 101))
X[:, 0] = np.array([0, 0, 0, vx0, 0, 0])
for k in range(X.shape[1] - 1):
X[:, k + 1] = F @ X[:, k]
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(X[0, :], X[1, :], X[2, :])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
Напомню, что для типа np.array символ "@" обозначает матричное перемножение. Расстояния и скорости измеряются в попугаях, угловая скорость в рад/с. Так же необходимо помнить, что для получения окружности надо чтобы вектора скорости и угловой скорости были перпендикулярны, иначе вместо окружности получится спираль.
В итоге задав некоторое начальное положение, скорость и угловую скорость можно получить такую траекторию
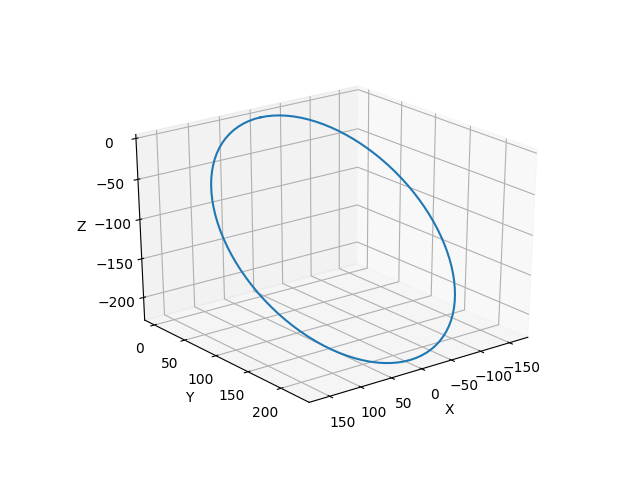
Точность совпадения первой и последних точек может быть получена как
>>> print(X[:3, 0] - X[:3,-1])
[-0.00051924 -0.0072984 0.0072984 ]
При радиусе поворота порядка 150 единиц относительная погрешность не превышает величин порядка $inline$5 cdot 10^{-5}$inline$. Этой точности вполне достаточно для модели ФК, следящего за поворачивающей целью.
Заключение
Если раньше ФК применялся в основном для решения задач навигации, где применение линейных моделей движения давало неплохой результат, то с развитием таких современных приложений как робототехника, компьютерное зрение и прочее увеличилась надобность и в более сложных моделях движения объектов. При этом применение вышеописанного подхода позволяет без особых затрат синтезировать дискретную модель ФК, что позволят облегчить разработчикам задачу. Единственное ограничение такого подхода заключается в том, что непрерывная модель динамической системы должна описываться набором линейных, или хотя бы линеаризуемых, уравнений в пространстве состояния.
Резюмируя вышесказанное можно привести алгоритм синтеза переходной матрицы ФК:
- Запись дифференциального уравнения системы
- Переход к вектору состояния и к пространству состояний
- Линеаризация в случае необходимости
- Представление матрицы перехода в виде матричной экспоненты и усечение ряда при необходимости
- Вычисление остальных матриц с учетом матрицы перехода
Автором приветствуется конструктивная критика в отношении допущенных ошибок, неточностей, неверных формулировок, не упомянутых методов и прочего. Спасибо за внимание!
Использованная литература
[1] Медич Дж. Статистически оптимальные линейные оценки и управление. Пер. с англ. Под ред. А.С. Шаталова Москва. Издательство «Энергия», 1973, 440 с.
[2] Матвеев В.В.Основы построения бесплатформенных инерциальных систем СПб.: ГНЦ РФ ОАО «Концерн „ЦНИИ Электроприбор“,2009. — 280с. ISBN 978-5-900180-73-3
Автор: fkeel





