В процессе изучения нейронных сетей возникла мысль, как бы применить их для чего-то практически интересного, и не столь заезженного и тривиального, как готовые датасеты от MNIST. Например, почему бы не распознавать азбуку Морзе.

Сказано, сделано. Для тех кому интересно, как с нуля создать работающий декодер CW, подробности под катом.
Повторить описанные ниже эксперименты может любой, для этого даже не нужно иметь радиоприемник. Все исходные файлы были записаны через websdr, где легко можно услышать радиолюбителей, например на частотах 7 и 14МГц. Там же есть кнопка Record, с помощью которой любой сигнал можно записать в формате wav.
Выделение сигнала из записи
Чтобы нейросеть могла распознать символы азбуки Морзе, сначала их надо выделить из исходной записи.
Загрузим данные из wav-файла и выведем его на экран.
from scipy.io import wavfile
import matplotlib.pyplot as plt
file_name = "websdr_recording_2019-08-17T16_26_52Z_14026.0kHz.wav"
fs, data = wavfile.read(file_name)
plt.plot(data)
plt.show()Если все было сделано правильно, мы увидим что-то типа такого:
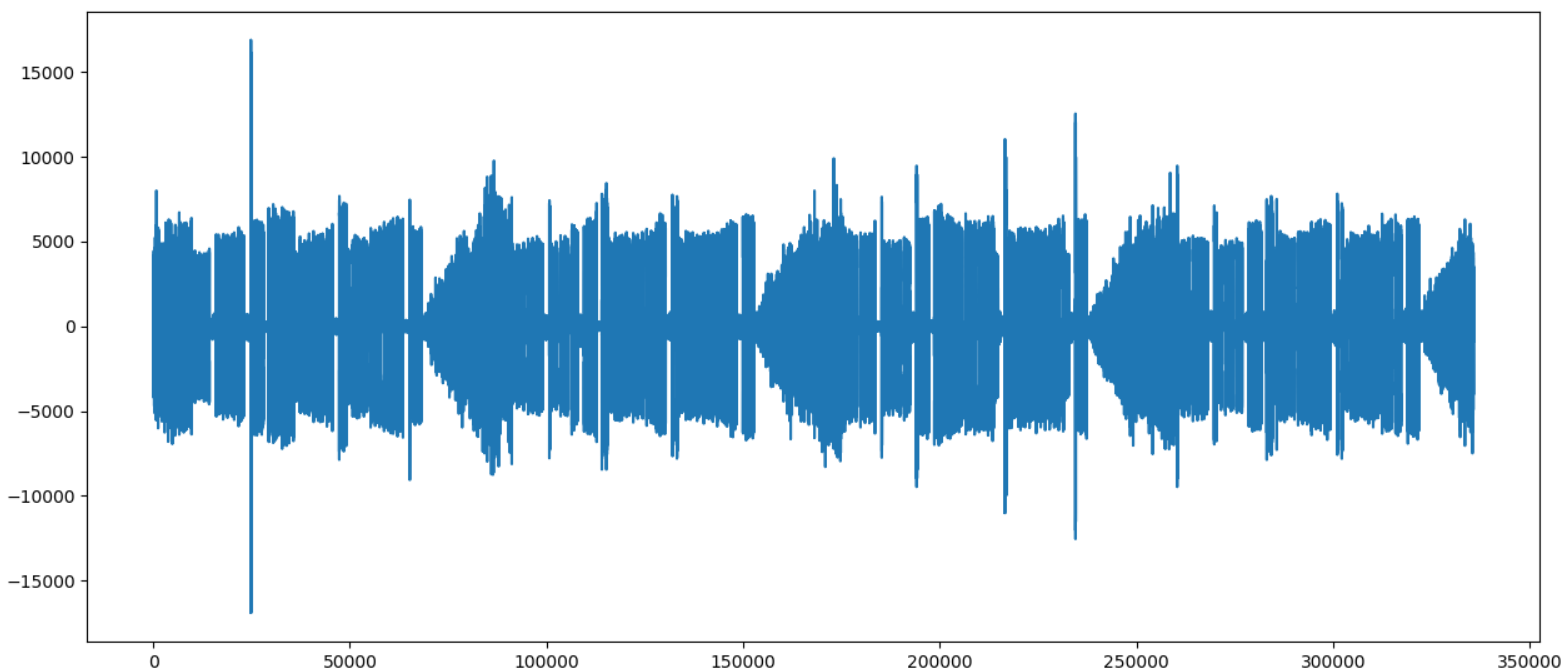
Исторически, сигнал азбуки Морзе это простейший вид модуляции, которую можно придумать — тон либо есть, либо его нет. Поэтому в записи может быть одновременно несколько сигналов, и они не мешают друг другу.

При записи сигналов CW я устанавливал частоту на 1КГц ниже и режим верхней боковой полосы (Upper Side Band), так что интересующий нас сигнал всегда находится в записи на частоте 1КГц. Выделим его с помощью полосового фильтра (фильтр Баттерворта).
from scipy.signal import butter, lfilter, hilbert
def butter_bandpass(lowcut, highcut, fs, order=5):
nyq = 0.5 * fs
low = lowcut / nyq
high = highcut / nyq
b, a = butter(order, [low, high], btype='band')
return b, a
def butter_bandpass_filter(data, lowcut, highcut, fs, order=5):
b, a = butter_bandpass(lowcut, highcut, fs, order)
y = lfilter(b, a, data)
return y
cw_freq = 1000
cw_width_hz = 50
data_filtered = butter_bandpass_filter(data, cw_freq - cw_width_hz, cw_freq + cw_width_hz, fs, order=5)
К получившемуся сигналу применяем преобразование Гильберта чтобы получить огибающую.
def hilbert_envelope(data):
analytical_signal = hilbert(data)
amplitude_envelope = np.abs(analytical_signal)
return amplitude_envelope
y_env = hilbert_envelope(data_filtered)
В результате получаем вполне узнаваемый сигнал кода Морзе:
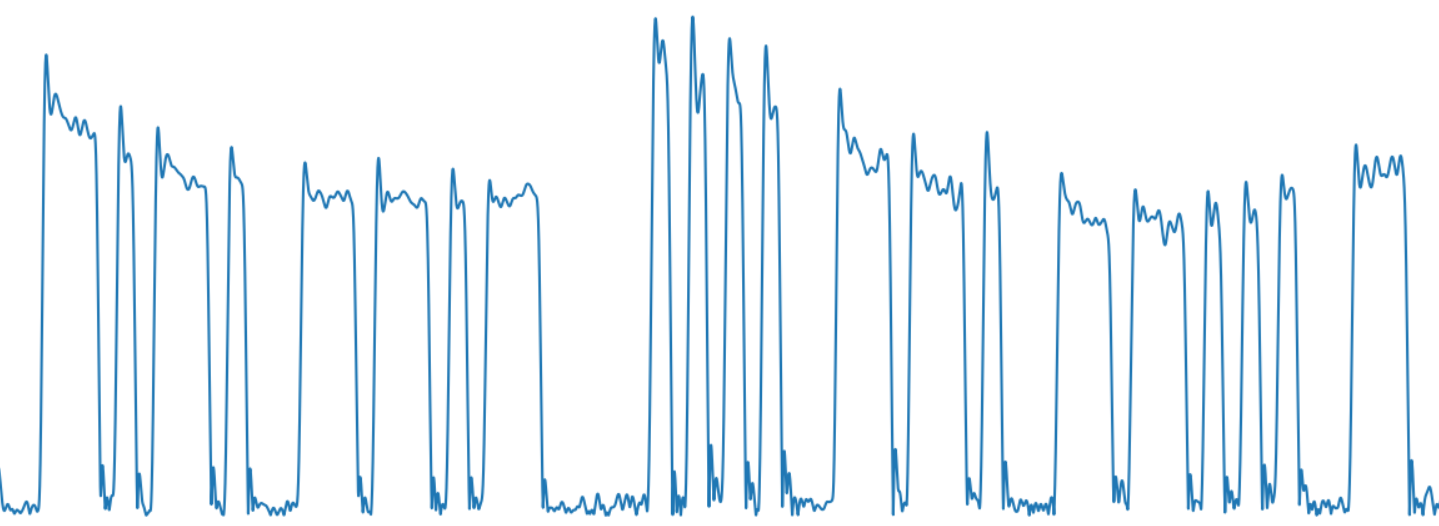
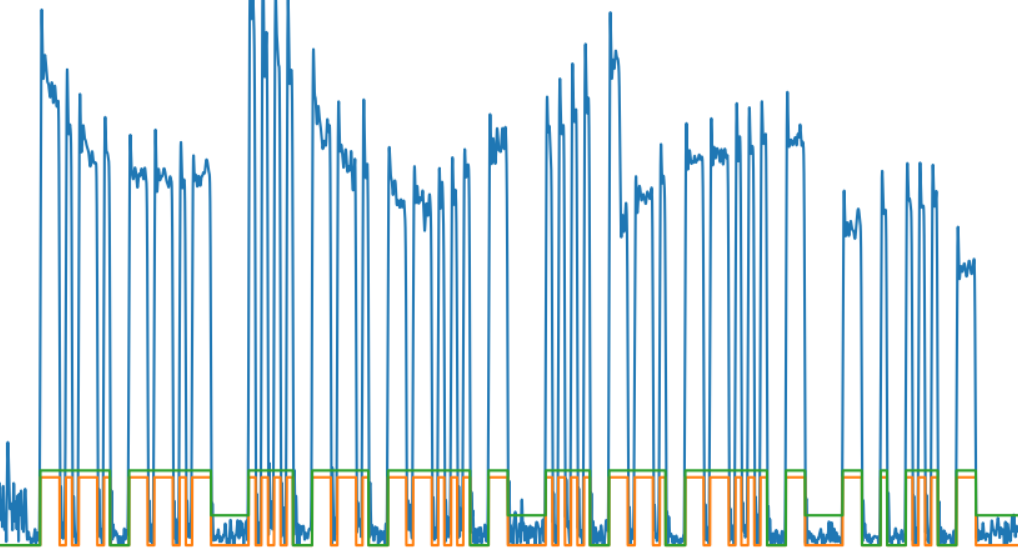
Следующей задачей является выделение отдельных символов. Сложность тут в том, что сигналы могут быть разного уровня — как видно на картинке, из-за особенностей распространения в атмосфере, уровень сигнала «плавает», он может затухнуть и усилиться вновь. Так что просто обрезать данные по некоторому уровню было бы недостаточно. Используем moving average («скользящее среднее») и фильтр низких частот чтобы получить сильно сглаженное текущее среднее значение сигнала.
def moving_average(a, n=3):
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
def butter_lowpass_filter(data, cutOff, fs, order=5):
b, a = butter_lowpass(cutOff, fs, order=order)
y = lfilter(b, a, data)
return y
ma_size = 5000
y_env2 = y_env # butter_lowpass_filter(y_env, 20, fs)
y_ma = moving_average(y_env2, n=ma_size) # butter_lowpass_filter(y_env, 1, fs)
y_ma2 = butter_lowpass_filter(y_ma, 2, fs)
# Enlarge array from right to the original size
y_ma3 = np.pad(y_ma2, (0, ma_size-1), 'mean')
Как можно видеть из картинки, результат вполне адекватный изменению сигнала:
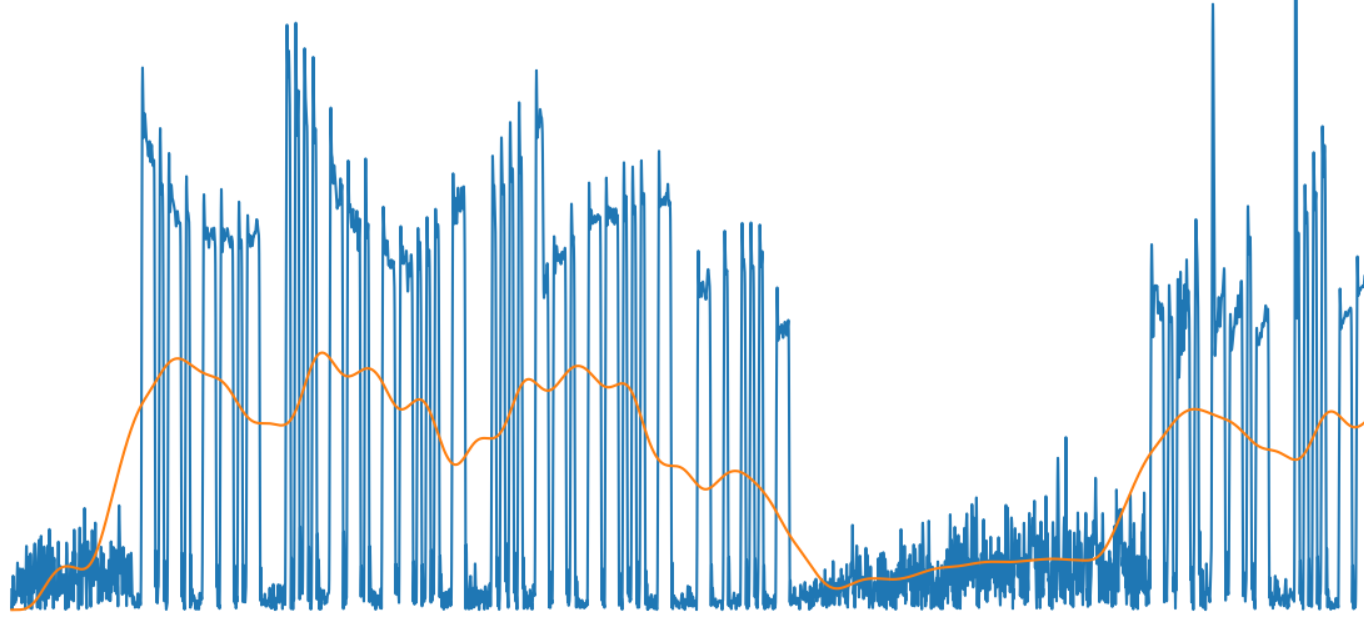
И наконец, последнее: получим битовый массив, показывающий наличие или отсутствие сигнала — считаем сигнал «единицей», если его уровень выше среднего.
y_normalized = y_ma3 < y_env2
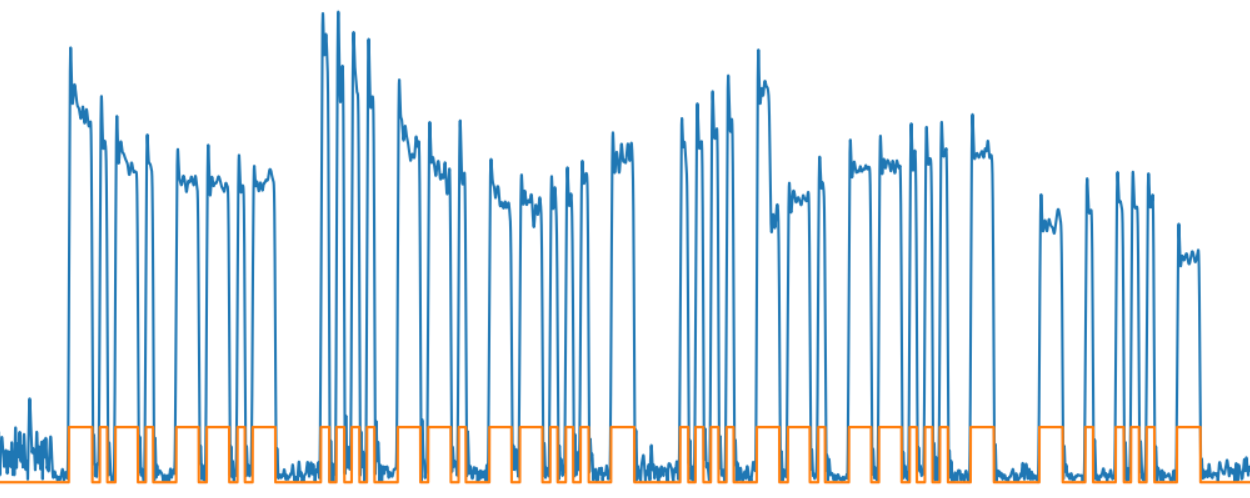
y_normalized2 = y_normalized.astype("int16")
Мы перешли от шумного и неодинакового по уровню входного сигнала к заметно более удобному для обработки сигналу цифровому.
Выделение символов
Следующая задача — выделить отдельные символы, для этого нужно знать скорость передачи. Существуют определенные правила соотношения длительности точек, тире и пауз в азбуке Морзе (подробнее тут), для упрощения я просто задаю длительность минимальной паузы в миллисекундах. Вообще, скорость может варьироваться даже в пределах одной записи (в радиопередаче участвуют минимум два абонента, настройки передатчиков которых могут отличаться). Скорость также может сильно отличаться для разных записей — опытный радист может передавать в 2-3 раза быстрее, чем начинающий.
Дальше все просто, код не претендует на красоту и изящество, но вполне работает. Выделяем подъем и спад сигналов, и в зависимости от длины, разделяем слова и символы.
min_len = 0.05
symbols = []
pos_start, pos_end, sym_start = -1, -1, -1
data_mask = np.zeros_like(y_env2) # For debugging
pause_min = int(min_len*fs)
sym_min, sym_max = 0, 10*min_len
margin = int(min_len*fs)
for p in range(len(y_normalized2) - 1):
if y_normalized2[p] < 0.5 and y_normalized2[p+1] > 0.5:
# Signal rize
pause_len = p - pos_end
if pause_len > pause_min:
# Save previous symbol if exist
if sym_start != -1 and pos_end != -1:
sym_len = (pos_end - pos_start)/fs
if sym_len > sym_min and sym_len < sym_max:
# print("Code found: %d - %d, %fs" % (sym_start, pos_end, (pos_end - pos_start) / fs))
data_out = y_env2[sym_start - margin:pos_end + margin]
symbols.append(data_out)
data_mask[sym_start:pos_end] = 1
# Add empty symbol at the word end
if pause_len > 3*pause_min:
symbols.append(np.array([]))
data_mask[pos_end:p] = 0.4
# New symbol started
sym_start = p
pos_start = p
if y_normalized2[p] > 0.5 and y_normalized2[p+1] < 0.5:
# Signal fall
pos_end = p
Это временное решение, т.к. в идеале скорость нужно определять динамически.
На картинке зеленой линией показана огибающая выделенных символов и слов.
В результате работы программы мы получаем список, каждый элемент которого представляет собой отдельный символ, выглядит это примерно так.

Эти данные уже вполне достаточны, чтобы обрабатывать и распознавать их нейросетью.
Текст получается достаточно длинным, так что продолжение (оно же окончание) во второй части.
Автор: DmitrySpb79





А где вторая часть ?