Добрый день!
Как и было обещано в предыдущей статье, сегодня мы продолжим разговор о методологиях, применяемых в A/B-тестировании и рассмотрим методы оценки результатов множественных экспериментов. Мы увидим, что методологии довольно просты, и математическая статистика не так страшна, а первооснова всего — аналитическое и здравый смысл. Однако предварительно хотелось бы сказать пару слов о том, какие же бизнес-задачи помогают решать строгие математические методы, нужны ли они Вам на данном этапе развития Вашей компании и какие pros and cons существуют в Большой аналитике.
«Кати в прод на все 100» или как спасти пару млрд для своей компании
В любом стартапе, летящем на безумной скорости, решения принимаются с такой же быстротой, а эффект вновь запущенной продуктовой фичи, как правило, настолько финансово ощутим, что дополнительные доказательства не требуются.
Однако в определенный момент времени компания достигает такого масштаба и охвата аудитории, что, во-первых, задача экспансии и поиска новых источников финансового роста на рынке в связи с его ограниченной ресурсоёмкостью становится всё более и более сложной, а, во-вторых, потери от неверно принятого решения становятся критическими — ведь без предварительного исследования, без учета статистической погрешности его результатов киллер-фича, расскатанная на продукт с аудиторией, с DAU в несколько миллионов может привести к оттоку пользователей, повышению bounce-rate и колосальным потерям в продуктовой выручке, которые только мультиплицируются в долгосрочной перспективе. В такой ситуации подход quick-and-dirty быстрой аналитики перестаёт приносить пользу и должен уступить место подходу вдумчивого и небыстрого, основательного data-анализа.
Кроме того, в крупных сервисах, которые ставят перед собой задачи стратегического долговременного планирования и грамотного распределения финансовых вложений между частями продукта, проведение кратко- и долгосрочных экспериментов является одной из важнейших задач. Однако за качество и надёжность принятого решения нередко приходится платить скоростью.
Следует отметить, что несмотря на заголовок данного абзаца, сфера применения A/B-тестов распространяется гораздо дальше за границы продуктовой аналитики: это и анализ качества прогнозных моделей для оценки будущего возврата инвестиций, и исследование эффективности финансовых вложений в различные части продукта и рекламные каналы его продвижения, аналитика дистрибуции, прогнозирование LTV, финансовое моделирование, оценка качества внедряемых ML-моделей scoring'а, ранжирования и многое другое.
Типология экспериментов: что, когда и зачем
Эксперименты бывают двух видов: проводимые с независимыми максимально консистентными друг относительно друга выборками в один и тот же момент времени и проводимые с зависимыми выборками или с одной и той же группой, но в разные моменты времени.
Типичный продуктовый A/B-эксперимент, исследующий влияние новой фичи на основные показатели, относится к экспериментам с независимыми выборками. Исследование же влияния фактора, в процессе которого невозможно отличить те группы, которые взаимодействовали с источником impact'а, и те, которые не взаимодействовали, а поэтому можно оценить влияние только исходя из метрик до и после, относится к исследованию с зависимыми выборками. Примером такого исследования может быть анализ результатов рекламной компании на ТВ. Ещё одним вариантом проведения эксперимента с зависимыми выборками может быть исследование в формате парных сравнений элементов между группами, в котором каждому элементу контрольной выборки ставится в соответствие элемент экспериментальной выборки.
Существуют также A/A-эксперименты и обратные эксперименты. Данные темы достаточно интересны, но мы не будем их подробно рассматривать в рамках данной статьи.
Кроме того, эксперименты могут проводиться как в формате A/B, так и в формате множественных сравнений, как и заявлено в заголовке статьи. Поскольку типичные методологии расчёта A/B-эксперимента были рассмотрены ранее, в это статье мы поговорим о методологиях расчёта множественных экспериментов и рекомендациях о границах их использования для решения бизнес-задач.
Множественные эксперименты: pros and cons
Как и было указано выше, иногда на практике проводят множественное сравнение
Следует отметить, что каждая новая сплит-группа, добавленная в исследование, снижает его точность, уменьшает репрезентативность выборки, а также повышает вероятность ошибки первого рода: для 

Зачем же проводить множественные эксперименты, если они снижают точность результатов нашего исследования?
Первой причиной может выступать желание бизнеса как можно скорее и дешевле получить ответ, какоое решение следует принять при наличии нескольких вариантов, сэкононив при этом время и себестоимость разработки и внедрения экперимента.
Второй причиной может выступать тестирование комбинаций — простейший пример: пользователю предлагается различное взаимное расположение двух элементов на лендинговой странице.
Кроме того, одной из задач проведения множественного теста, хотя и спорных с точки зрения точности оценки по ряду причин, может быть желание провести A/A/B — параллельное проведение исследований A/A и A/B с целью убедиться в достоверности результатов и устранить вероятность ложно-положительного результата (вспомним знаменитую статью Дэвида Кодави о A/A).
Простые методы оценки множественых тестов
Сегодня мы рассмотрим типичную и широко распространённую задачу внедрения новой фичи с целью увеличения выручки компании за счёт повышения количества целевых монетизируемых действий. На входе имеем три группы пользователей, которым были предложены 3 разных варианта выдачи с предложением нажать на кнопку звонка по объявлению.
Для проверки множественных гипотез используются подходы из теории дисперсионного анализа, иначе именуемого ANOVA. При этом в большинстве случаев происходит расчёт и проверка групповой вероятности ошибки первого рода FWER.
Суть FWER довольно проста: мы оцениваем вероятность появления false-positive результатов, ошибок первого рода. Исходя из принципа построения данного критерия используется несколько методик оценки результата стат.значимости теста. Расмотрим два самых простых и популярных метода.
Посмотрим на то, как же менялась ислледуемая метрика в динамике, построив графики в интерактивной библиотеке plotly:
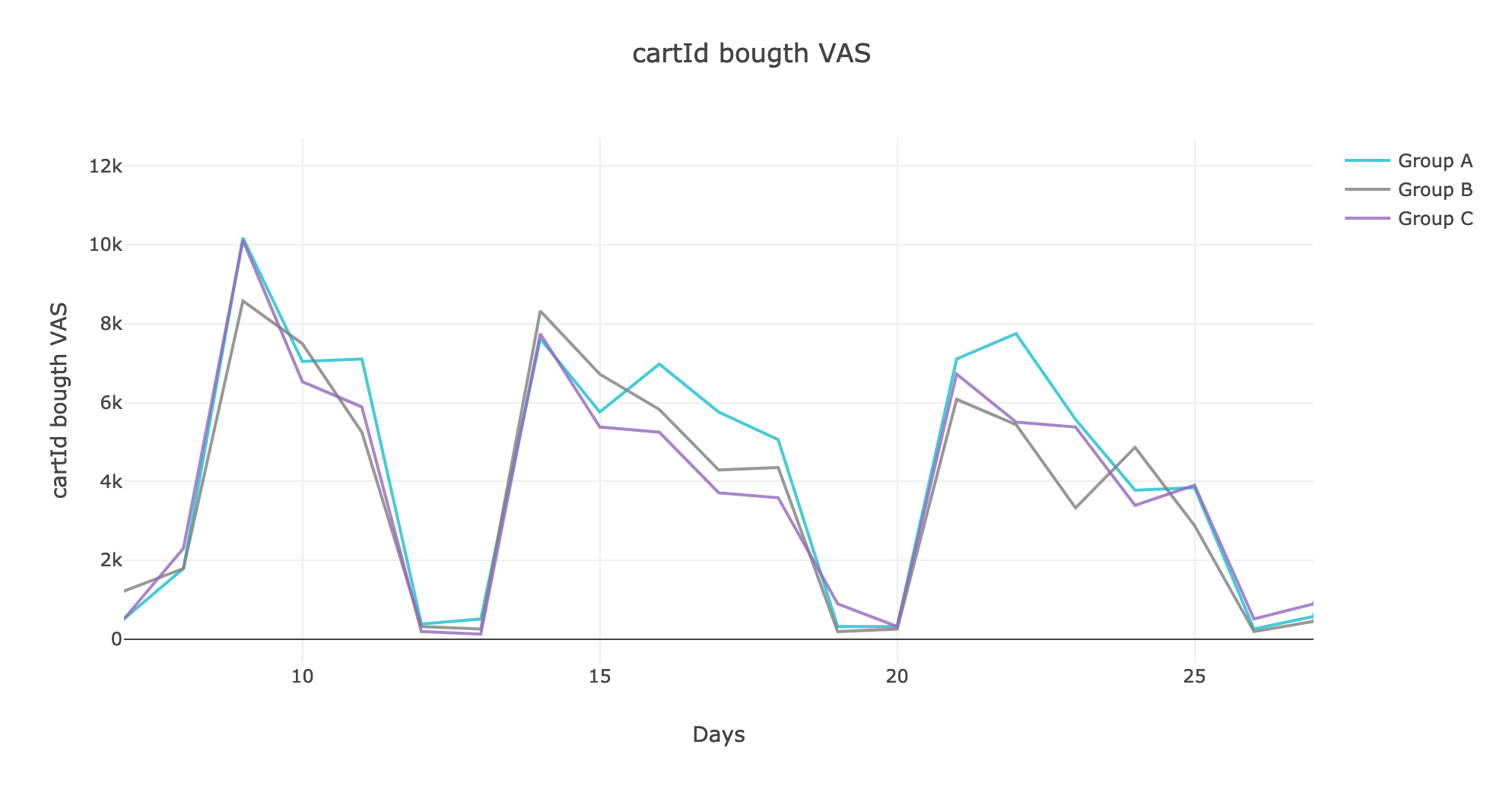
Опытный взгляд заметит слабое преобладание группы A в одной из недель.
Посмотрим на наличие различий в целевых действиях, представив данные в виде box-plot'ов:
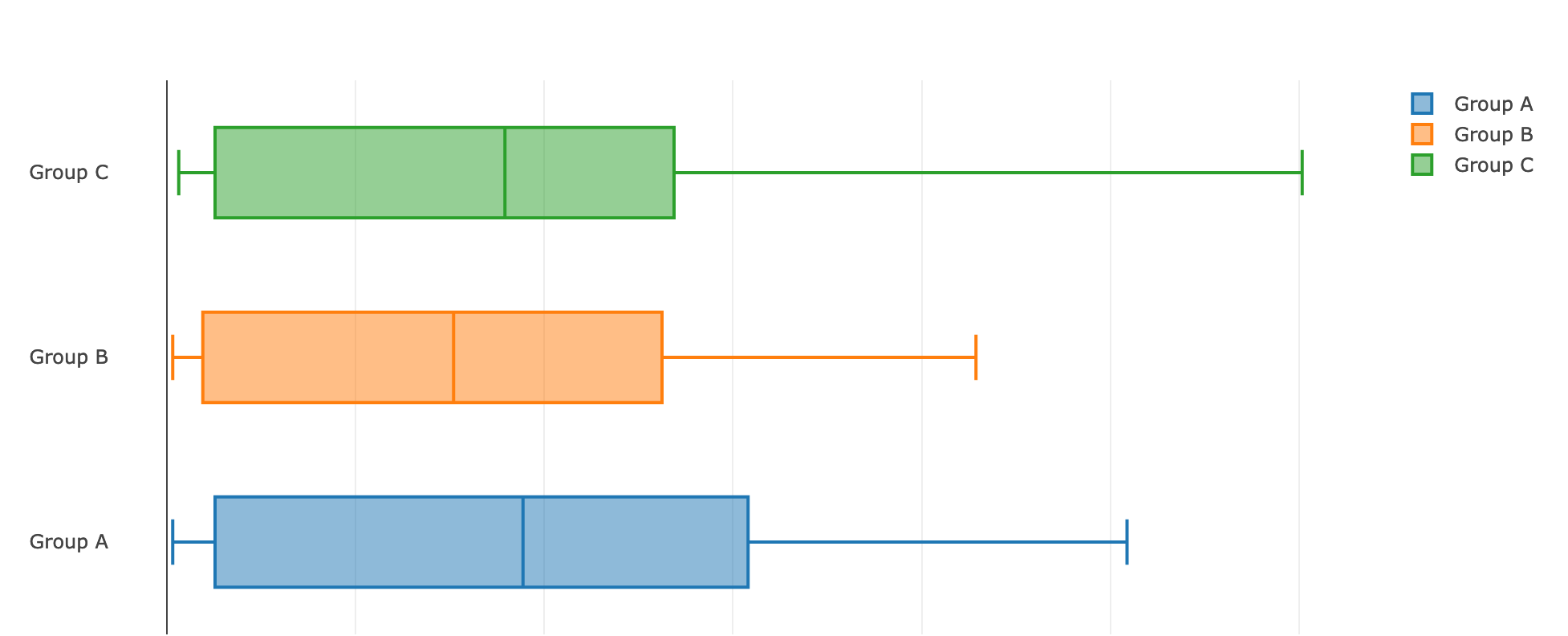
Мы видим, что эффект действительно присутствует, а значит, нам нужно оценить, какова вероятность, что результаты действительно различаются.
Первоначально воспользуемся тестом для проверки равенства дисперсий:
stats.levene(df['action_count'][df['bucket'] == '0'],
df['action_count'][df['bucket'] == '1'],
df['action_count'][df['bucket'] == '2'])Результаты теста не стат. значимы, следовательно дисперсии в подгруппах однородны. На этот раз мы воспользовались критерием Левена, который менее чувствителен к отклонению метрики в выборках от нормального распределения, чем критерий Барлетта. Кстати, критерий Левена родился в 1960 и скоро отпразднует свой 60-летний юбилей.
Воспользуемся проверками на нормальность, приведём распределение нашего критерия в выборке к нормальному виду одним из методов, описанных в нашей предыдущей статье и преступим к непосредственному анализу статистической значимости результатов.
1. Поправка Бонферрони
Простой метод, позволяющий оценить вероятнсть ложного положительного прокраса эксперимета. Его суть можно описать простой формулой:
Основным минусом данного подхода является то, что при увеличении 
Реализовать данный подход можно простым методом «из коробки» при помощи Twitter Bootstrap:
bs_01_estims = bs.bootstrap_ab(df[(df['bucket']=='0')].action_count.values,
df[(df['bucket']=='1')].action_count.values,
bs_stats.mean,
bs_compare.difference, num_iterations=5000, alpha=0.05/3,
iteration_batch_size=100, scale_test_by=1, num_threads=4)
bs_12_estims = bs.bootstrap_bc(df[(df['bucket']=='1')].action_count.values,
df[(df['bucket']=='2')].action_count.values,
bs_stats.mean,
bs_compare.difference, num_iterations=5000, alpha=0.05/3,
iteration_batch_size=100, scale_test_by=1, num_threads=4)
bs_02_estims = bs.bootstrap_ac(df[(df['bucket']=='0')].action_count.values,
df[(df['bucket']=='2')].action_count.values,
bs_stats.mean,
bs_compare.difference, num_iterations=5000, alpha=0.05/3,
iteration_batch_size=100, scale_test_by=1, num_threads=4)
Получив статистические оценки, можно сделать выводы о наличии или отсутствии различий между группами.
2. Метод Холма
Метод Холма можно назвать развитием идеи, заложенной в методе поправки Бонферрони на множественную проверку гипотез. Его принцип довольно прост: итеративная проверка гипотез до момента достяжения порога 
N_buckets = 3
for i in range(N_buckets):
bs_data[i] = bs.bootstrap(df[(df['bucket']=='i')].action_count.values,
stat_func=bs_stats.mean,
num_iterations=10000, iteration_batch_size=300, return_distribution=True)
print(stats.kstest(bs_data[i]))
print(stats.shapiro(bs_data[i]))
st_01, pval_01 = stats.ttest_ind(bs_data[0], bs_data[1])
st_12, pval_12 = stats.ttest_ind(bs_data[1], bs_data[2])
st_02, pval_02 = stats.ttest_ind(bs_data[0], bs_data[2])
Кстати, после bootstrap'ирования гистограммы и графики приняли более читаемый вид:
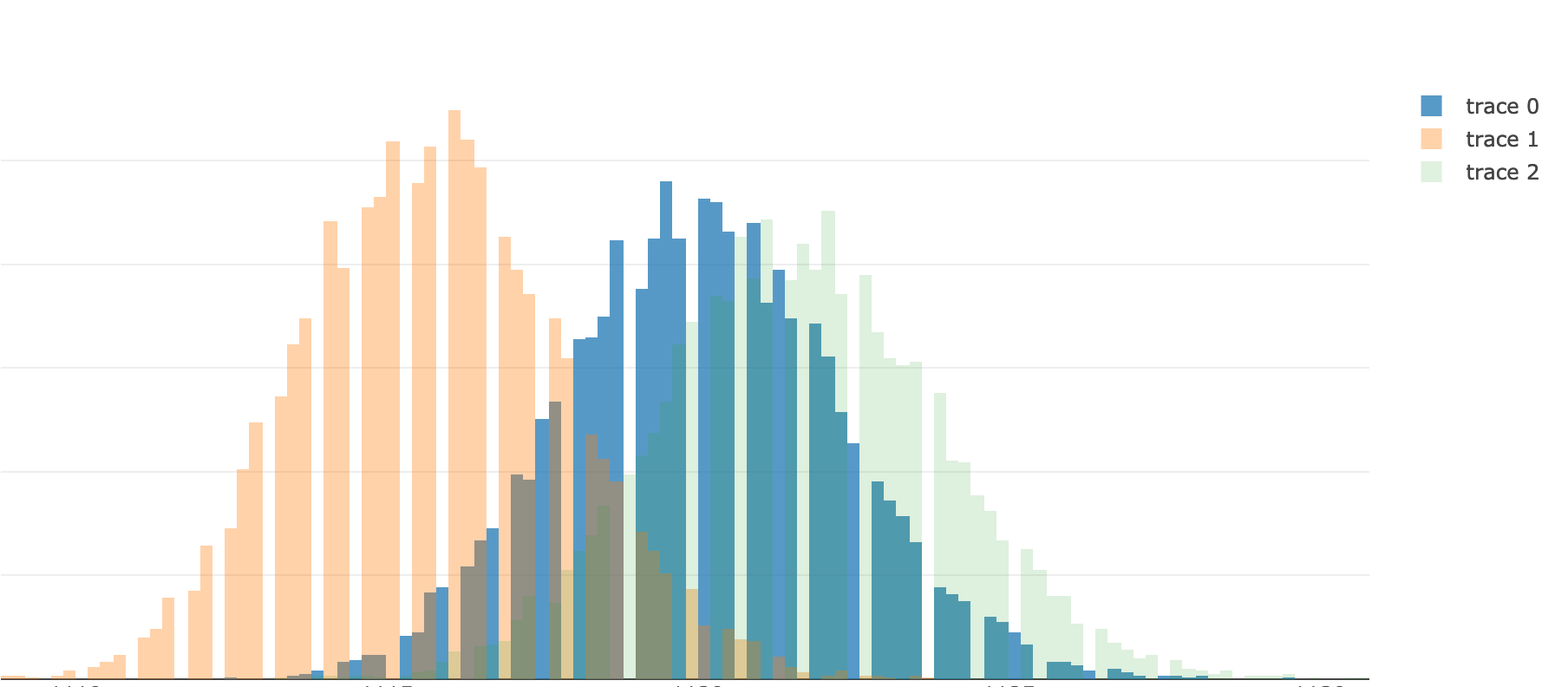
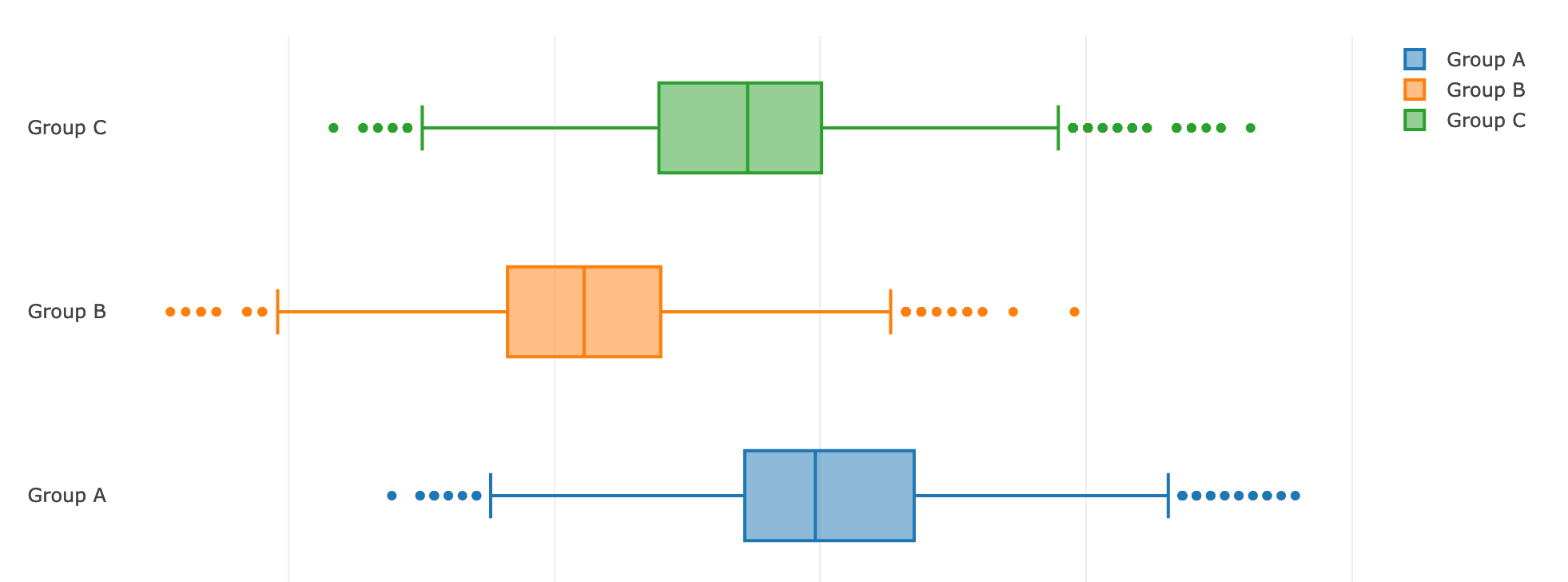
3. Метод Краскела-Уоллиса
Ещё один из методов, которые можно применять для оценки результатов статистического теста, это метод Краскела-Уоллиса. Его можно найти в стандартной библиотеке
scipy.statsstats.kruskal()Реализация проверки этим методом показалась достаточна изящной, подскажу: вам потребуется ещё два шага для осуществления проверки, а также дополнительная функция из модуля библиотеки statsmodels. Приглашаю Вас прочитать статью о методе и реализовать эту проверку самостоятельно, Вам понравится :)
Следует отметить также, что аналогично можно воспользоваться критерием Манна-Уитни.
Хочу задать вопрос любознательному читателю: чем критерий Манна-Уитни отличается от критерия Краскела-Уоллиса? Всё просто, но предлагаю Вам проверить свою эрудицию и ответить на этот вопрос самостоятельно :)
Зачем мы проводим эти перекрёстные проверки различными тестами? Ответ очевиден — можно пробовать проводить A/A и исследовать, пригоден ли данный тест для наших данных, можно воспользоваться трюком, разбив offline одну групп на подгруппы и проведя исследование чувствительноости и точности теста на них, а можно пробовать как бы валидировать тесты друг другом.
В качестве послесловия и напутствия
Следует отметить, что в погоне за поиском стат. значимости в изменении целевой метрики аналитики часто упускают важный факт — иногда исследуемое изменение влияет не только или совсем не на ту метрику, которую планировалось увеличить/уменьшить, а на другую: например, у нас могут вырасти суммарные деньги, но при этом упасть конверсия — то есть пользователи стали оплачивать более дорогую услугу или товар, но мы потеряли какую-то часть пользователей, которые приносили нам деньги. Здесь следует понимать, что выиграв в краткосрочном периоде, в долгосрочной перспективе мы можем получить просадку в выручке — возможно, количество пользователей, которые покупают более дорогую услугу на сервисе, ограничено, и в какой-то момент времени мы упрёмся в «потолок» рынка. Второй неблагожелательный вариант в рассматриваемом случае — более дорогой товар служит дольше дешёвого FMCG и приобретается реже, а значит мы снова упрёмся в ограничения рынка.
Следует понимать, что если мы оперируем большим числом метрик, как обычно бывает в интернет-проектах, то какая-либо из них обязательно прокрасится. В таком случае, вторым шагом для принятия решения может служить как конструирование дополнительной модели над текущим тестом (что, как правило, дороже по времени), так и визуальная проверка глазами наиболее важных метрик — например, финансовой составляющей.
На сегодня это всё, о чём хотелось Вам рассказать.
Всем наилучшие пожелания!
Автор: Dilemma







