Привет, Хаброжители! Байесовские методы пугают формулами многих айтишников, но без анализа статистики и вероятностей сейчас не обойтись. Кэмерон Дэвидсон-Пайлон рассказывает о байесовском методе с точки зрения программиста-практика, работающего с многофункциональным языком PyMC и библиотеками NumPy, SciPy и Matplotlib. Раскрывая роль байесовских выводов при А/В-тестировании, выявлении мошенничества и в других насущных задачах, вы не только легко разберетесь в этой нетривиальной теме, но и начнете применять полученные знания для достижения своих целей.
Отрывок: 4.3.3. Пример: сортировка комментариев на Reddit
Возможно, вы не согласны, что закон больших чисел применяется всеми, хотя и только неявно, при подсознательном принятии решений. Рассмотрим пример онлайн-рейтингов товаров. Часто ли вы доверяете среднему рейтингу в пять баллов на основе одного отзыва? Двух отзывов? Трех отзывов? Вы подсознательно понимаете, что при таком малом количестве отзывов средний рейтинг плохо отражает то, насколько товар на самом деле хорош/плох.
Вследствие этого возникают упущения при сортировке товаров и вообще при их сравнении. Для многих покупателей понятно, что сортировка результатов интерактивного поиска по рейтингу не слишком объективна, неважно, идет ли речь о книгах, видео или комментариях в Интернете. Зачастую находящиеся на первых местах фильмы или комментарии получают высокие оценки только за счет небольшого числа восторженных поклонников, а действительно хорошие фильмы или комментарии скрыты на последующих страницах с якобы неидеальными рейтингами около 4,8. Что же с этим делать?
Рассмотрим популярный сайт Reddit (я осознанно не привожу на него ссылки, ведь Reddit печально знаменит тем, что затягивает пользователей, и я боюсь, что вы никогда не вернетесь к моей книге). На этом сайте есть множество ссылок на разные истории и картинки, причем комментарии к этим ссылкам тоже очень популярны. Пользователи сайта (которых обычно называют словом redditor1) могут голосовать за каждый комментарий или против него (так называемые голоса «за» (upvotes) и голоса «против» (downvotes)). Reddit по умолчанию сортирует комментарии по убыванию. Как же определить, какие комментарии лучшие? Обычно ориентируются на следующие несколько показателей.
1. Популярность. Комментарий считается хорошим, если за него подано много голосов. Проблемы при использовании этой модели начинаются в случае комментария с сотнями голосов «за» и тысячами «против». Хотя и очень популярный, этот комментарий, похоже, слишком неоднозначен, чтобы считаться «лучшим».
2. Разница. Можно воспользоваться разницей между количеством голосов «за» и «против». Это решает проблему, возникающую при использовании метрики «популярность», но не учитывает временную природу комментариев. Комментарии могут быть отправлены через многие часы после публикации первоначальной ссылки. При этом возникает смещение, из-за которого самый высокий рейтинг получают вовсе не лучшие комментарии, а самые старые, успевшие накопить больше голосов «за», чем более новые.
3. Поправка на время. Рассмотрим метод, при котором разница голосов «за» и «против» делится на возраст комментария и получается частота (rate), например величина разницы в секунду или в минуту. Сразу же на ум приходит контрпример: при использовании варианта «в секунду» комментарий, оставленный секунду назад с одним голосом «за» окажется лучше, чем оставленный 100 секунд назад с 99 голосами «за». Избежать этой проблемы можно, если учитывать только комментарии, оставленные как минимум t секунд назад. Но как выбрать хорошее значение t? Значит ли это, что все комментарии, оставленные позднее, чем t секунд назад, плохи? Дело закончится сравнением неустойчивых величин с устойчивыми (новых и старых комментариев).
4. Соотношение. Ранжирование комментариев по соотношению числа голосов «за» к суммарному числу голосов «за» и «против». Такой подход устраняет проблему с временно'й природой комментариев, так что недавно оставленные комментарии с хорошими оценками получат высокий рейтинг с той же вероятностью, что и оставленные давно, при условии, что у них относительно высокое отношение голосов «за» к общему числу голосов. Проблема с этим методом состоит в том, что комментарий с одним голосом «за» (отношение = 1,0) окажется лучше, чем комментарий с 999 голосами «за» и одним «против» (отношение = 0,999), хотя очевидно, что второй из этих комментариев скорее окажется лучшим.
Я неспроста написал «скорее». Может оказаться и так, что первый комментарий с одним-единственным голосом «за» действительно лучше, чем второй, с 999 голосами «за». С этим утверждением трудно согласиться, ведь мы не знаем, какими могли бы быть 999 потенциальных следующих голосов для первого комментария. Скажем, он мог получить в результате еще 999 голосов «за» и ни одного голоса «против» и оказаться лучше, чем второй, хотя такой сценарий и не слишком вероятен.
На самом деле нам нужно оценить фактическое соотношение голосов «за». Отмечу, что это вовсе не то же, что наблюдаемое соотношение голосов «за»; фактическое соотношение голосов «за» скрыто, наблюдаем мы только число голосов «за» по сравнению с голосами «против» (фактическое соотношение голосов «за» можно рассматривать как вероятность получения данным комментарием голоса «за», а не «против»). Благодаря закону больших чисел можно с уверенностью утверждать, что у комментария с 999 голосами «за» и одним «против» фактическое соотношение голосов «за», вероятно, будет близко к 1. С другой стороны, мы гораздо менее уверены в том, каким окажется фактическое соотношение голосов «за» для комментария с одним голосом «за». Похоже, что это байесовская задача.
Один из способов определить априорное распределение соотношения голосов «за» — изучить историю распределения соотношений голосов «за». Это можно сделать с помощью скрапинга комментариев Reddit и последующего определения распределения. Впрочем, у этого метода есть несколько недостатков.
1. Асимметричные данные. Число голосов у абсолютного большинства комментариев очень невелико, вследствие чего соотношения у многих комментариев будут близки к экстремальным (см. «треугольный» график в примере с набором данных Kaggle на рис. 4.4) и распределение окажется сильно «перекошено». Можно попробовать учитывать лишь комментарии, число голосов у которых превышает определенное пороговое значение. Но и здесь возникают сложности. Приходится искать баланс между числом доступных комментариев, с одной стороны, и более высоким пороговым значением с соответствующей точностью соотношения — с другой.
2. Смещенные (содержащие систематическую погрешность) данные. Reddit состоит из множества подфорумов (subreddits). Два примера: r/aww с фотографиями забавных животных и r/politics. Более чем вероятно, что поведение пользователей при комментировании этих двух подфорумов Reddit будет кардинально различаться: в первом из них посетители, скорее всего, будут умиляться и вести себя дружелюбно, что приведет к большему числу голосов «за», по сравнению со вторым, где мнения в комментариях, вероятно, будут расходиться.
В свете вышеизложенного мне кажется, что имеет смысл воспользоваться равномерным априорным распределением.
Теперь мы можем вычислить апостериорное распределение фактического соотношения голосов «за». Сценарий comments_for_top_reddit_pic.py служит для скрапинга комментариев из текущей наиболее популярной картинки Reddit. В следующем коде мы произвели скрапинг комментариев Reddit, относящихся к картинке [3]: http://i.imgur.com/OYsHKlH.jpg.
from IPython.core.display import Image
# С помощью добавления числа к вызову %run
# можно получить i-ю по рейтингу фотографию.
%run top_pic_comments.py 2[Output]: Title of submission: Frozen mining truck http://i.imgur.com/OYsHKlH.jpg
"""
Contents: массив текстов всех комментариев к картинке Votes: двумерный
массив NumPy голосов "за" и "против" для каждого комментария
"""
n_comments = len(contents)
comments = np.random.randint(n_comments, size=4)
print "Несколько комментариев (из общего числа в %d) n
-----------"%n_comments
for i in comments:
print '"' + contents[i] + '"'
print "голоса "за"/"против": ",votes[i,:]
print[Output]: Несколько комментариев (из общего числа 77) ----------- "Do these trucks remind anyone else of Sly Cooper?" голоса "за"/"против": [2 0] "Dammit Elsa I told you not to drink and drive." голоса "за"/"против": [7 0] "I've seen this picture before in a Duratray (the dump box supplier) brochure..." голоса "за"/"против": [2 0] "Actually it does not look frozen just covered in a layer of wind packed snow." голоса "за"/"против": [120 18]
При N голосах и заданном фактическом соотношении голосов «за» p число голосов «за» напоминает биномиальную случайную переменную с параметрами p и N (дело в том, что фактическое соотношение голосов «за» эквивалентно вероятности подачи голоса «за» по сравнению с голосом «против» при N возможных голосах/испытаниях). Создадим функцию для байесовского вывода по p в отношении набора голосов «за»/«против» конкретного комментария.
import pymc as pm
def posterior_upvote_ratio(upvotes, downvotes, samples=20000):
"""
Эта функция принимает в качестве параметров количество
голосов "за" и "против", полученных конкретным комментарием,
а также количество выборок, которое нужно вернуть пользователю.
Предполагается, что априорное распределение равномерно.
"""
N = upvotes + downvotes
upvote_ratio = pm.Uniform("upvote_ratio", 0, 1)
observations = pm.Binomial("obs", N, upvote_ratio,
value=upvotes, observed=True)
# Обучение; сначала выполняем метод MAP, поскольку он не требует
# больших вычислительных затрат и приносит определенную пользу.
map_ = pm.MAP([upvote_ratio, observations]).fit()
mcmc = pm.MCMC([upvote_ratio, observations])
mcmc.sample(samples, samples/4)
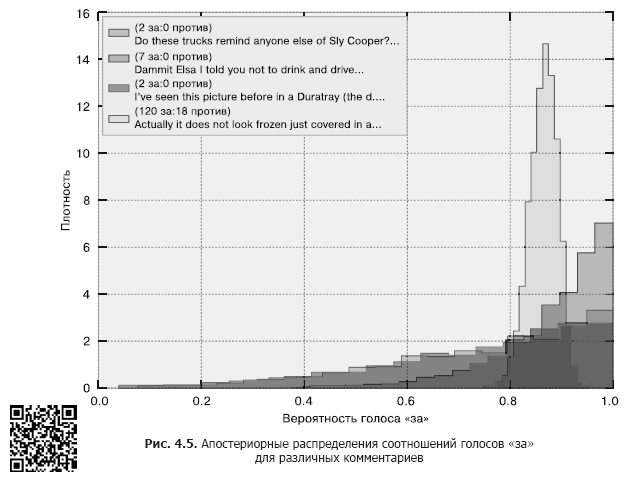
return mcmc.trace("upvote_ratio")[:]Далее приведены получившиеся в результате апостериорные распределения.
figsize(11., 8)
posteriors = []
colors = ["#348ABD", "#A60628", "#7A68A6", "#467821", "#CF4457"]
for i in range(len(comments)):
j = comments[i]
label = u'(%d за:%d против)n%s...'%(votes[j, 0], votes[j,1],
contents[j][:50])
posteriors.append(posterior_upvote_ratio(votes[j, 0], votes[j,1]))
plt.hist(posteriors[i], bins=18, normed=True, alpha=.9,
histtype="step", color=colors[i%5], lw=3, label=label)
plt.hist(posteriors[i], bins=18, normed=True, alpha=.2,
histtype="stepfilled", color=colors[i], lw=3)
plt.legend(loc="upper left")
plt.xlim(0, 1)
plt.ylabel(u"Плотность")
plt.xlabel(u"Вероятность голоса 'за'")
plt.title(u"Апостериорные распределения соотношений голосов 'за'
для различных комментариев");[Output]: [****************100%******************] 20000 of 20000 complete
Как видно из рис. 4.5, некоторые распределения сильно «сжаты», у других же — сравнительно длинные «хвосты», выражающие то, что мы точно не знаем, чему равно фактическое соотношение голосов «за».
4.3.4. Сортировка
До сих пор мы игнорировали основную цель нашего примера: сортировку комментариев от лучшего к худшему. Конечно, невозможно сортировать распределения; сортировать нужно скалярные значения. Предусмотрено множество способов извлечь сущность распределения в виде скаляра; например, можно выразить суть распределения через его математическое ожидание, или среднее значение. Впрочем, среднее значение для этого подходит плохо, поскольку этот показатель не учитывает неопределенность распределений.
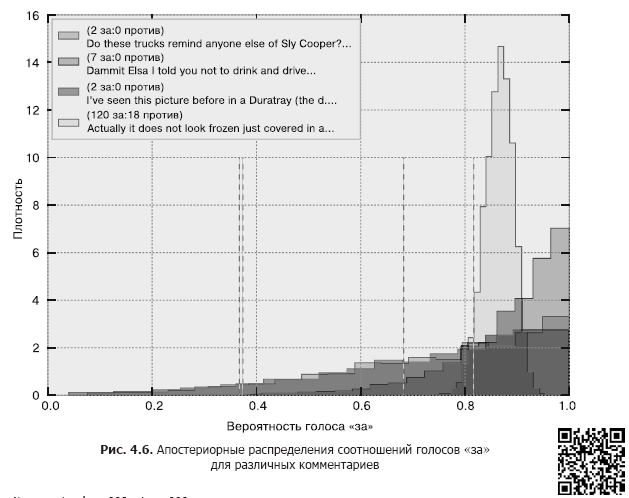
Я рекомендовал бы воспользоваться 95%-ным наименее правдоподобным значением (least plausible value), которое определяется как значение с лишь 5%-ной вероятностью того, что фактическое значение параметра ниже его (ср. с нижней границей байесовского доверительного интервала). Далее мы строим графики апостериорных распределений с указанным 95%-ным наименее правдоподобным значением (рис. 4.6).
N = posteriors[0].shape[0]
lower_limits = []
for i in range(len(comments)):
j = comments[i]
label = '(%d за:%d против)n%s…'%(votes[j, 0], votes[j,1],
contents[j][:50])
plt.hist(posteriors[i], bins=20, normed=True, alpha=.9,
histtype="step", color=colors[i], lw=3, label=label)
plt.hist(posteriors[i], bins=20, normed=True, alpha=.2,
histtype="stepfilled", color=colors[i], lw=3)
v = np.sort(posteriors[i])[int(0.05*N)]
plt.vlines(v, 0, 10 , color=colors[i], linestyles="—",
linewidths=3)
lower_limits.append(v)
plt.legend(loc="upper left")
plt.ylabel(u"Плотность")
plt.xlabel(u"Вероятность голоса 'за'")
plt.title(u"Апостериорные распределения соотношений голосов 'за'
для различных комментариев");
order = np.argsort(-np.array(lower_limits))
print order, lower_limits[Output]: [3 1 2 0] [0.36980613417267094, 0.68407203257290061, 0.37551825562169117, 0.8177566237850703]
Лучшими, согласно нашей процедуре, окажутся те комментарии, для которых наиболее высока вероятность получения высокого процента голосов «за». Визуально это комментарии с ближайшим к единице 95%-ным наименее правдоподобным значением. На рис. 4.6 95%-ное наименее правдоподобное значение изображено с помощью вертикальных линий.
Почему же сортировка на основе этого показателя — такая хорошая идея? Упорядочение в соответствии с 95%-ным наименее правдоподобным значением означает максимальную осторожность в объявлении комментариев лучшими. То есть даже при наихудшем сценарии, если мы сильно переоценили соотношение голосов «за», гарантируется, что лучшие комментарии окажутся сверху. При таком упорядочении обеспечиваются следующие весьма естественные свойства.
1. Из двух комментариев с одинаковым наблюдаемым соотношением голосов «за» лучшим будет признан комментарий с бо'льшим числом голосов (поскольку выше уверенность в более высоком соотношении для него).
2. Из двух комментариев с одинаковым количеством голосов лучшим считается комментарий с бо'льшим числом голосов «за».
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 25% по купону — Python
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Автор: ph_piter
