Главная

Создаем с нуля собственную нейронную сеть на Python

2019-04-29 в 6:19, admin, рубрики: data mining, data science, python, искусственный интеллект, машинное обучение, нейронная сеть, нейронная сеть с нуля, Питон

Всем привет!

На повестке дня интересная тема — будем создавать с нуля собственную нейронную сеть на Python. В ее основе обойдемся без сложных библиотек (TensorFlow и Keras).

Перед тем как углубиться, рекомендую освежить знания по искусственным нейронным сетям и подписаться на мой телеграм-канал (@dataisopen), чтобы не пропустить интересных статей.

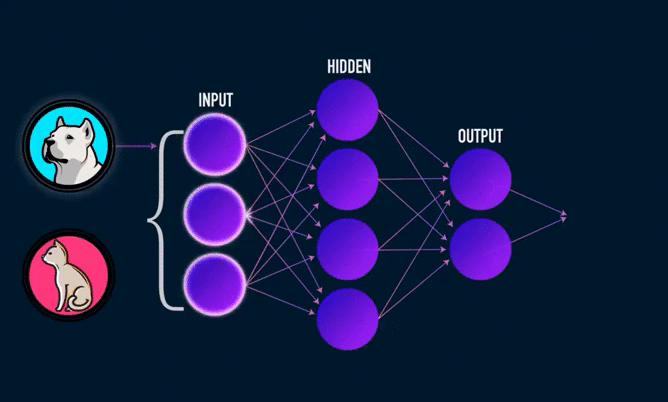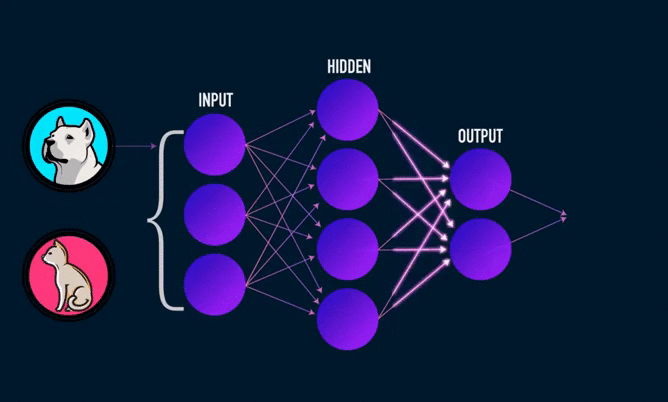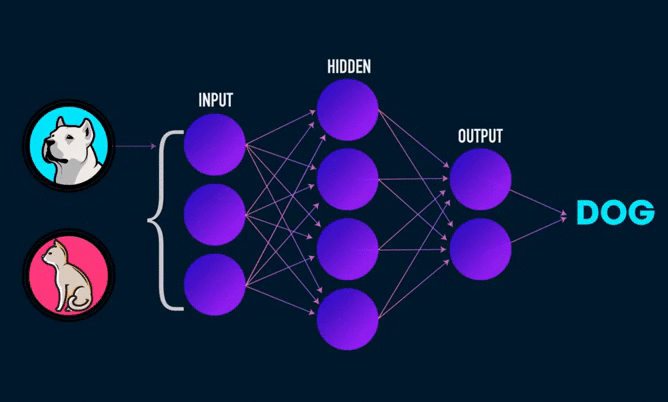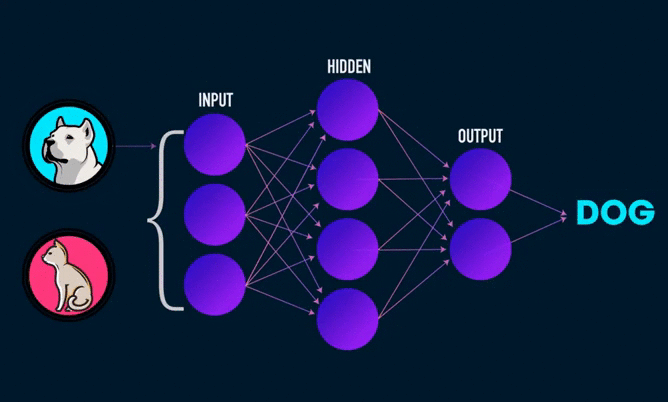
Основное, о чем нужно знать — искусственная нейронная сеть может быть представлена в виде блоков/кружков (искусственных нейронов), имеющие между собой, в определенном направлении, связи. В работе биологической нейронной сети от входов сети к выходам передается электрический сигнал (в процессе прохода он может изменяться).

Электрические сигналы в связях искусственной нейронной сети — это числа. Ко входам нашей искусственной нейронной сети мы будем подавать рандомные числа (которые бы символизировали величины электрического сигнала, если бы он был). Эти числа, продвигаясь по сети будут неким образом меняться. На выходе мы получим ответ нашей сети в виде какого-то числа.

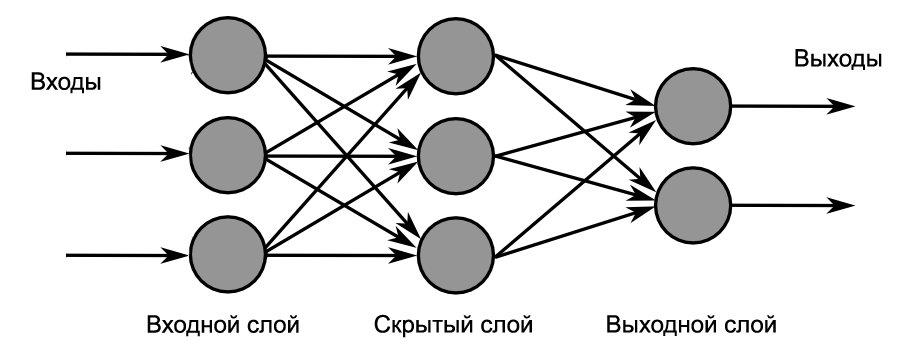
Искусственный нейрон

Для того, чтобы нам понять как работает нейронная сеть изнутри — внимательно изучим модель искусственного нейрона:

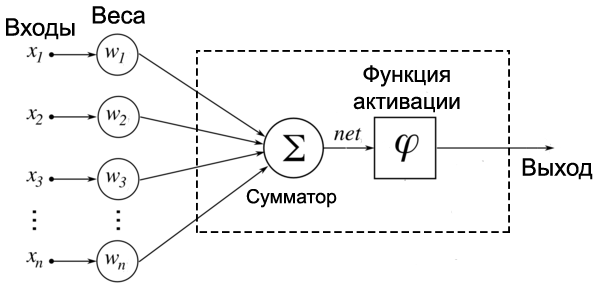
Поступающие на вход рандомные числа умножаются на свои веса. Сигнал первого входа $x_1$ умножается на соответствующий этому входу вес $w_1$ . В итоге получаем $x_1 w_1$ . И так до $n$ -ого входа. В итоге на последнем входе получаем $x_n w_n$ .

После этого все произведения передаются в сумматор, который суммирует все входные числа, умноженные на соответствующие веса:

$x_1w_1+x_2w_2+cdots+x_nw_n=sumlimits^n_{i=1}x_iw_i$

Справка по Сигме.

Итогом работы сумматора является число, называемое взвешенной суммой:

$net=sumlimits^n_{i=1}x_iw_i$

Отмечу, что просто так подавать взвешенную сумму на выход бессмысленно. Нейрон должен обработать ее и получить адекватный выходной сигнал. Для этих целей используют функцию активации (мы будем использовать Sigmoid).

Функция активации (Activation function) — функция, принимающая взвешенную сумму как аргумент. Значение этой функции и является выходом нейрона .

Обучение нейронной сети

Обучение нейронной сети представляет собой процесс тонкой настройки весов и смещений из входных данных. Конечно, правильные значения для весов и смещений определяют точность предсказаний.

Выход у двухслойной нейронной сети будет выглядеть следующим образом:

$inline$ŷ = σ (W_2σ( W_1x+b_1)+b_2)$inline$

$x$ — входной слой;
$ŷ$ — выходной слой;
$W$ — набор весов;
$b$ — набор смещений;
$σ$ — выбор функции активации для каждого скрытого слоя.

Как мы видим веса $W$ и смещения $b$ являются единственными переменными, которые влияют на выход $ŷ$ .

Для информации, результат повторного применения обучающего процесса состоит из 2-х шагов:

Вычисление прогнозируемого выхода ;
Обновление весов и смещений.

Опишем все это в коде:

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

Оценивать качество наших результатов (набор весов и смещений, который минимизирует функцию потери) мы будем вместе с суммой квадратов ошибок (среднее значение разницы между каждым прогнозируемым и фактическим значением):

$Sum - of- Squares Error=sumlimits^n_{i=1}(y-ŷ)^2$

Далее, после измерения ошибки нашего прогноза, нам нужно найти способ распространения ошибки обратно и обновить наши веса и смещения. В этом нам поможет градиентный спуск.

Здесь мы не сможем вычислить функции потерь по отношению к весам и смещениям, так как её уравнение не содержит весов и смещений.

Ура! Мы получили то, что нам нужно — производную функции потерь по отношению к весам. Теперь мы сможем регулировать веса.

Добавим функцию backpropagation в наш код:

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

    def backprop(self):
        d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * sigmoid_derivative(self.output)))
        d_weights1 = np.dot(self.input.T,  (np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1)))

        self.weights1 += d_weights1
        self.weights2 += d_weights2

На этом наша сеть готова. Выводы по качеству нейронной сети предлагаю каждому сделать самостоятельно.

Всем знаний!

Ответ

1500 итераций:

Прогноз/Факт
0.023/0
0.979/1
0.975/1
0.025/0

Автор: Syurmakov

Источник