Вариационные автокодировщики: теория и рабочий код

в 10:42, , рубрики: python, sgd, VAE, вариационный автокодировщик, генерация рукописных цифр, машинное обучение, нейросеть прямого распространения, обработка изображений

Вариационные автокодировщики: теория и рабочий код - 1

Вариационный автокодировщик (автоэнкодер) — это генеративная модель, которая учится отображать объекты в заданное скрытое пространство.

Когда-нибудь задавались вопросом, как работает модель вариационного автокодировщика (VAE)? Хотите знать, как VAE генерирует новые примеры, подобные набору данных, на котором он обучался? Прочитав эту статью, вы получите теоретическое представление о внутренней работе VAE, а также сможете реализовать его самостоятельно. Затем я покажу рабочий код VAE, обученный на наборе рукописных цифр, и мы немного повеселимся, генерируя новые цифры!

Генеративные модели

VAE представляет собой генеративную модель — она оценивает плотность вероятности (PDF) обучающих данных. Если такая модель обучена на натуральных изображениях, то присвоит изображению льва высокое значение вероятности, а изображению случайной ерунды — низкое значение.

Модель VAE также умеет брать примеры из обученной PDF, что является самой крутой частью, так как она сможет генерировать новые примеры, похожие на исходный набор данных!

Я объясню VAE, используя набор рукописных цифр MNIST. Входными данными для модели являются картинки в формате $mathbb{R}^{28×28}$. Модель должна оценить вероятность, насколько входные данные похожи на цифру.

Задача моделирования изображений

Взаимодействие между пикселями представляет трудную задачу. Если пиксели независимы друг от друга, то нужно изучать PDF каждого пикселя независимо, что легко. Выборка тоже простая — берём отдельно каждый пиксель.

Но в цифровых изображениях есть чёткие зависимости между пикселями. Если вы увидите начало четвёрки на левой половине, то очень удивитесь, если правая половина является завершением нуля. Но почему?..

Скрытое пространство

Вы знаете, что на каждом изображение есть одна цифра. Вход в $mathbb{R}^{28×28}$ явно не содержит этой информации. Но она должна где-то находиться… Это «где-то» — скрытое пространство.

Вариационные автокодировщики: теория и рабочий код - 4

Вы можете думать о скрытом пространстве как о $mathbb{R}^{k}$, где каждый вектор содержит $k$ частей информации, необходимой для отрисовки изображения. Предположим, первое измерение содержит число, представленное цифрой. Вторым измерением может быть ширина. Третьим — угол, и так далее.

Можем представить процесс рисования человеком цифры в два шага. Сначала человек определяет — сознательно или нет — все атрибуты цифры, которую собирается выевсти. Далее эти решения трансформируются в штрихи на бумаге.

VAE пытается смоделировать этот процесс: при заданном изображении $x$ мы хотим найти хотя бы один скрытый вектор, способный его описать; один вектор, содержащий инструкции для генерации $x$. Сформулировав его по формуле полной вероятности, мы получаем $P(x)=int P(x|z)P(z)dz$.

Давайте вложим разумный смысл в это уравнение:

  • Интеграл означает, что кандидатов нужно искать во всём скрытом пространстве.
  • Для каждого кандидата $z$ мы задаём вопрос: можно ли сгенерировать $x$, используя инструкции $z$? Достаточно ли велико $P (x|z)$? Например, если $z$ кодирует информацию о цифре 7, то изображение 8 невозможно. Однако допустимо изображение 1, потому что 1 и 7 похожи.
  • Мы нашли хорошее $z$? Отлично! Но подождите секунду… насколько это $z$ вероятно? $P(z)$ достаточно велико? Рассмотрим изображение перевернутой цифры 7. Идеальным соответствием станет скрытый вектор, описывающий вид 7, где размер угла установлен на 180°. Однако такое $z$ маловероятно, потому что обычно цифры не пишут под углом 180°.

Целью обучения VAE является максимизация $P(x)$. Будем моделировать $P(x|z)$ с помощью многомерного гауссовского распределения $mathcal{N}(f(z), sigma^2 cdot I)$.

$f(z)$ моделируется с использованием нейронной сети. $sigma$ — это гиперпараметр для умножения единичной матрицы $I$.

Следует иметь в виду, что $f$ — это то, что мы будем использовать для генерации новых изображений с помощью обученной модели. Наложение гауссовского распределения служит только для учебных целей. Если мы возьмём дельта-функцию Дирака (т.е. детерминированное $x=f(z)$), то не сможем обучать модель с помощью градиентного спуска!

Чудеса скрытого пространства

У подхода со скрытым пространством есть две большие проблемы:

  1. Какую информацию содержит каждое измерение? Некоторые измерения могут относиться к абстрактным элементам, например, к стилю. Даже если бы было легко интерпретировать все измерения, мы не хотим назначать метки набору данных. Такой подход не масштабируется на другие наборы данных.
  2. Скрытое пространство может быть запутано, когда между измерениями есть корреляция. Например, очень быстро нарисованная цифра может одновременно привести к появлению и угловых, и более тонких штрихов. Определить эти зависимости сложно.

На помощь приходит глубокое обучение

Оказывается, каждое распределение можно сгенерировать путём применения достаточно сложной функции на стандартном многомерном гауссовском распределении.

Выберем $P(z)$ в качестве стандартного многомерного гауссовского распределения. Таким образом, моделируемое нейросетью $f$ можно разбить на две фазы:

  1. Первые слои отображают гауссововское распределение в истинное распределение по скрытому пространству. Мы не сможем интерпретировать измерения, но это не имеет значения.
  2. Последующие слои будут отображаться из скрытого пространства в $P(x|z)$.

Так как мы обучим этого зверя?

Формула для $P(x)$ неразрешима, поэтому аппроксимируем её методом Монте-Карло:

  1. Отбор ${z_i}_{i=1}^n$ из предыдущего $P(z)$
  2. Апроксимация с помощью $P(x) approx frac{1}{n}sum_{i=1}^n P(x|z_i)$

Отлично! Итак, просто попробуем много разных $z$ и начнём вечеринку обратного распространения ошибки!

К сожалению, поскольку $x$ очень многомерно, для получения разумного приближения требуется много выборок. Я имею в виду, если вы пробуете $z$, то каковы шансы получить изображение, которое выглядит как-то похоже на $x$? Это, кстати, объясняет, почему $P(x|z)$ должно присваивать положительное значение вероятности любому возможному изображению, иначе модель не сможет обучаться: выборка $z$ приведёт к изображению, которое почти наверняка отличается от $x$, и если вероятность равна 0, то градиенты не смогут распространяться.

Как же решить эту проблему?

Cрежем путь!

Вариационные автокодировщики: теория и рабочий код - 41

Большинство образцов $z$ из выборки ничего не добавят в $P(x)$ — они слишком далеко за его границами. Вот если бы знать заранее, откуда их отбирать…

Можно ввести $Q(z|x)$. Данное $Q$ будет обучено присваивать высокие значения вероятности тем $z$, которые с большой вероятностью сгенерируют $x$. Теперь можно провести оценку по методу Монте-Карло, забирая гораздо меньше образцов из $Q$.

К сожалению, возникает новая проблема! Вместо максимизации $P(x)=int P(x|z)P(z)dz=mathbb{E}_{z sim P(z)} P(x|z)$ мы максимизируем $mathbb{E}_{z sim Q(z|x)} P(x|z)$. Как они связаны друг с другом?

Вариационный вывод

Вариационный вывод — это тема отдельной статьи, поэтому я не буду здесь подробно останавливаться на нём. Скажу только, что эти распределения связаны таким уравнением:

$log P(X) - mathcal{KL}[Q(z|x) || P(z|x)]=mathbb{E}_{z sim Q(z|x)}[log P(x|z)] - mathcal{KL}[Q(z|x) || P(z)]$

$mathcal{KL}$ является расстоянием Кульбака — Лейблера, которое интуитивно оценивает схожесть двух распределений.

Через мгновение вы увидите, как максимизировать правую часть уравнения. При этом левая сторона также максимизируется:

  • $P(x)$ максимизируется.
  • насколько далеко $Q(z|x)$ от $P(z|x)$ — настоящее априорное неизвестное — будет минимизировано.

Смысл правой части уравнения в том, что у нас здесь напряжение:

  1. С одной стороны мы хотим максимизировать, насколько хорошо $x$ должно декодироваться из $z sim Q$.
  2. С другой стороны, мы хотим, чтобы $Q(z|x)$ (кодировщик) был похож на предыдущее $P(z)$ (многомерное гауссовское распределение). Это можно рассматривать как регуляризацию.

Минимизация расходимости $mathcal{KL}$ выполняется легко при правильном выборе распределений. Мы будем моделировать $Q(z|x)$ как нейронную сеть, выход которой является параметрами многомерного гауссовского распределения:

  • среднее $mu_Q$
  • диагональная ковариационная матрица $Sigma_Q$

Затем расходимость $mathcal{KL}$ становится аналитически разрешимой, что отлично для нас (и для градиентов).

Часть декодера немного сложнее. На первый взгляд хочется заявить, что эта задача неразрешима методом Монте-Карло. Но выборка $z$ из $Q$ не позволит градиентам распространяться через $Q$, потому что выборка не является дифференцируемой операцией. Это проблема, поскольку тогда не смогут обонлявться веса слоев, выдающих $Sigma_Q$ и $mu_Q$.

Трюк новой параметризации

Мы можем заменить $Q$ детерминированным параметризованным преобразованием беспараметрической случайной величины:

  1. Выборка из стандартного (без параметров) гауссовского распределения.
  2. Умножение выборки на квадратный корень $Sigma_Q$.
  3. Добавление к результату $mu_Q$.

В результате получим распределение, равное $Q$. Теперь операция выборки происходит из стандартного гауссовского распределения. Следовательно, градиенты смогут распространяться через $Sigma_Q$ и $mu_Q$, так как теперь это детерминированные пути.

Результат? Модель сможет научиться настраивать параметры $Q$: она будет концентрироваться вокруг хороших $z$, которые способны производить $x$.

Объединяем всё вместе

Модель VAE бывает трудно понять. Мы рассмотрели здесь много материала, который трудно переварить.

Позвольте резюмировать все шаги для реализации VAE.

Вариационные автокодировщики: теория и рабочий код - 79

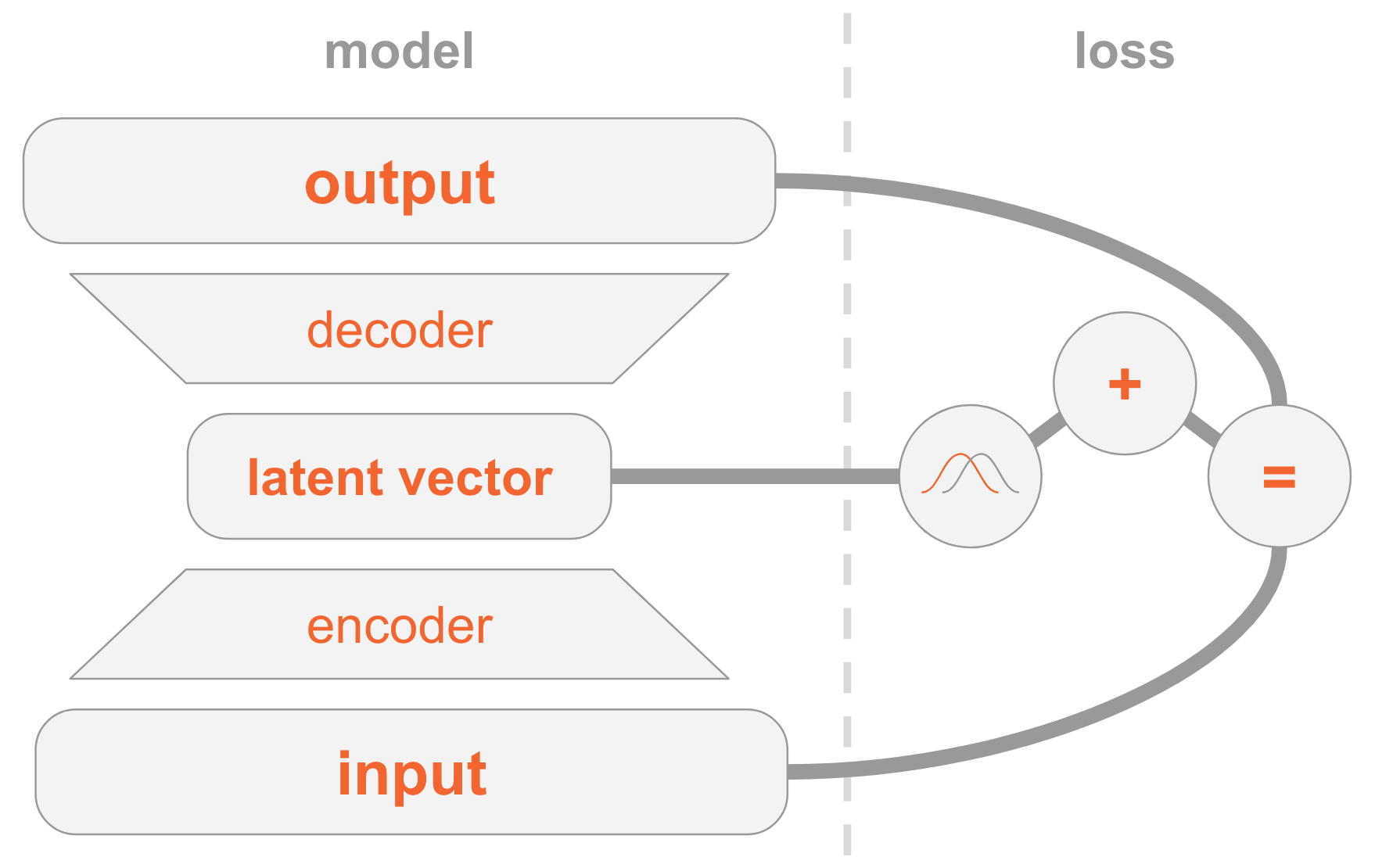
Слева у нас определение модели:

  1. Входное изображение передаётся через сеть кодировщика.
  2. Кодировщик выдаёт параметры распределения $Q(z|x)$.
  3. Скрытый вектор $z$ берётся из $Q(z|x)$. Если кодировщик хорошо обучен, то в большинстве случае $z$ содержат описание $x$.
  4. Декодер декодирует $z$ в изображение.

С правой стороны у нас функция потери:

  1. Ошибка восстановления: выходные данные должны быть аналогичны входным.
  2. $Q(z|x)$ должно быть аналогично предыдущему, то есть многомерному стандартному нормальному распределению.

Для создания новых изображений можно непосредственно выбрать скрытый вектор из предыдущего распределения и декодировать его в изображение.

Рабочий код

Теперь более подробно изучим VAE и рассмотрим рабочий код. Вы поймёте все технические детали, необходимые для реализации VAE. В качестве бонуса покажу интересный трюк: как назначить некоторым измерениям скрытого вектора особые роли, чтобы модель начала генерировать картинки указанных цифр.

import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt

np.random.seed(42)
tf.set_random_seed(42)

%matplotlib inline

Напоминаю, что модели обучаются на MNIST — наборе рукописных цифр. Входные изображения поступают в формате $mathbb{R}^{28×28}$.

mnist = input_data.read_data_sets('MNIST_data')
input_size = 28 * 28
num_digits = 10

Далее определим гиперпараметры.

Не стесняйтесь играться с разными значениями, чтобы получить представление о том, как они влияют на модель.

params = {
    'encoder_layers': [128],                # кодировщик на простой сети прямого распространения
    'decoder_layers': [128],                # как и декодер (CNN лучше, но не хочу усложнять код)
    'digit_classification_layers': [128],   # нужно для условий, объясню позже
    'activation': tf.nn.sigmoid,            # функция активации используется всеми подсетями
    'decoder_std': 0.5,                     # стандартное отклонение P(x|z) обсуждалось выше
    'z_dim': 10,                            # размерность скрытого пространства
    'digit_classification_weight': 10.0,    # нужно для условий, объясню позже
    'epochs': 20,
    'batch_size': 100,
    'learning_rate': 0.001
}

Модель

Вариационные автокодировщики: теория и рабочий код - 88

Модель состоит из трех подсетей:

  1. Получает $x$ (изображение), кодирует его в распределение $Q(z|x)$ по скрытому пространству.
  2. Получает $z$ в скрытом пространстве (кодовое представление изображения), декодирует его в соответствующее изображение $f(z)$.
  3. Получает $x$ и определяет цифру по сопоставлению с 10-мерным слоем, где i-е значение содержит вероятность i-го числа.

Первые две подсети — основа чистого VAE.

Третья представляет собой вспомогательную задачу, которая использует некоторые из скрытых измерений для кодирования цифры, найденной в изображении. Объясню зачем: ранее мы обсуждали, что нам всё равно, какую информацию содержит каждое измерение скрытого пространства. Модель может научиться кодировать любую информацию, которую она считает ценной для своей задачи. Поскольку мы знакомы с набором данных, то знаем важность измерения, которое содержит тип цифры (то есть её численное значение). И теперь мы хотим помочь модели, предоставив ей эту информацию.

По заданному типу цифры мы прямо кодируем её, то есть используем вектор размером 10. Эти десять чисел связаны со скрытым вектором, поэтому при декодировании этого вектора в изображение модель будет использовать цифровую информацию.

Есть два способа предоставить модели вектор прямого кодирования:

  1. Добавить его в качестве входных данных в модель.
  2. Добавить его как метку, так что модель сама вычислит прогноз: мы добавим другую подсеть, которая прогнозирует 10-мерный вектор, где функция потери — это перекрёстная энтропия с ожидаемым вектором прямого кодирования.

Выберем второй вариант. Почему? Ну, тогда при тестировании можно использовать модель двумя способами:

  1. Указать изображение в качестве входных данных и вывести скрытый вектор.
  2. Указать скрытый вектор в качестве входных данных и сгенерировать изображение.

Поскольку мы хотим поддерживать и первый вариант, то не можем давать модели цифру в качестве входных данных, поскольку не хотим знать её во время тестирования. Следовательно, модель должна научиться предсказывать её.

def encoder(x, layers):
    for layer in layers:
        x = tf.layers.dense(x,
                            layer,
                            activation=params['activation'])
    mu = tf.layers.dense(x, params['z_dim'])
    var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim']))
    return mu, var


def decoder(z, layers):
    for layer in layers:
        z = tf.layers.dense(z,
                            layer,
                            activation=params['activation'])
    mu = tf.layers.dense(z, input_size)
    return tf.nn.sigmoid(mu)


def digit_classifier(x, layers):
    for layer in layers:
        x = tf.layers.dense(x,
                            layer,
                            activation=params['activation'])
    logits = tf.layers.dense(x, num_digits)
    return logits

images = tf.placeholder(tf.float32, [None, input_size])
digits = tf.placeholder(tf.int32, [None])

# кодируем изображение в распределение по скрытому пространству
encoder_mu, encoder_var = encoder(images,
                                  params['encoder_layers'])

# отбираем вектор из скрытого пространства, используя
# трюк с повторной параметризацией
eps = tf.random_normal(shape=[tf.shape(images)[0],
                              params['z_dim']],
                       mean=0.0,
                       stddev=1.0)
z = encoder_mu + tf.sqrt(encoder_var) * eps

# classify the digit
digit_logits = digit_classifier(images,
                                params['digit_classification_layers'])
digit_prob = tf.nn.softmax(digit_logits)

# декодируем в изображение скрытый вектор, связанный
# с классификацией цифр
decoded_images = decoder(tf.concat([z, digit_prob], axis=1),
                         params['decoder_layers'])

# потеря состоит в том, насколько хорошо мы 
# можем восстановить изображение
loss_reconstruction = -tf.reduce_sum(
    tf.contrib.distributions.Normal(
        decoded_images,
        params['decoder_std']
    ).log_prob(images),
    axis=1
)

# и как далеко распределение по скрытому пространству от предыдущего.
# Если предыдущее является стандартным гауссовским распределением, 
# а в результате получается нормальное распределение с диагональной
# конвариантной матрицей, то KL-расхождение становится аналитически
# разрешимым, и мы получаем
loss_prior = -0.5 * tf.reduce_sum(
    1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var,
    axis=1
)

loss_auto_encode = tf.reduce_mean(
    loss_reconstruction + loss_prior,
    axis=0
)

# digit_classification_weight используется как вес между двумя потерями,
# поскольку между ними есть напряжение
loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean(
    tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits,
                                                   logits=digit_logits),
    axis=0
)

loss = loss_auto_encode + loss_digit_classifier

train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss)

Обучение

Вариационные автокодировщики: теория и рабочий код - 94

Обучим модель оптимизации двух функций потерь — VAE и классификации — с помощью SGD.

В конце каждой эпохи отбираем скрытые векторы и декодируем их в изображения, чтобы визуально наблюдать, как улучшается генеративная сила модели по эпохам. Метод отбора проб выглядит следующим образом:

  1. Явно задать измерения, которые используются для классификации по цифре, которую мы хотим сгенерировать. Например, если мы хотим создать изображение цифры 2, то задаём измерения $[0010000000]$.
  2. Произвести случайную выборку из других измерений многомерного нормального распределения. Это значения для разных цифр, которые генерируются в данной эпохе. Так мы получим представление о том, что закодировано в других измерениях, например, стиль почерка.

Смысл шага 1 заключается в том, что после конвергенции модель должна уметь классифицировать цифру во входном изображении по этим установкам измерений. При этом они также используются на этапе декодирования для создания изображения. То есть подсеть декодера знает: когда измерения соответствуют цифре 2, она должна сгенерировать картинку с этой цифрой. Поэтому если вручную установить измерения на цифру 2, мы получим сгенерированное изображение этой цифры.

samples = []
losses_auto_encode = []
losses_digit_classifier = []
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in xrange(params['epochs']):
        for _ in xrange(mnist.train.num_examples / params['batch_size']):
            batch_images, batch_digits = mnist.train.next_batch(params['batch_size'])
            sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits})
        
        train_loss_auto_encode, train_loss_digit_classifier = sess.run(
            [loss_auto_encode, loss_digit_classifier],
            {images: mnist.train.images, digits: mnist.train.labels})
        
        losses_auto_encode.append(train_loss_auto_encode)
        losses_digit_classifier.append(train_loss_digit_classifier)
        
        sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1])
        gen_samples = sess.run(decoded_images,
                               feed_dict={z: sample_z, digit_prob: np.eye(num_digits)})
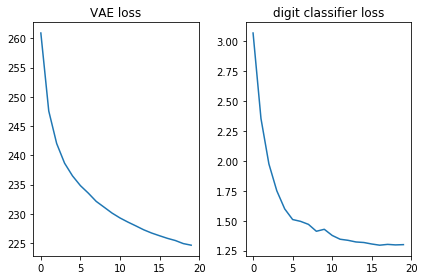
        samples.append(gen_samples)

Давайте проверим, что обе функции потери выглядят хорошо, то есть уменьшаются:

plt.subplot(121)
plt.plot(losses_auto_encode)
plt.title('VAE loss')

plt.subplot(122)
plt.plot(losses_digit_classifier)
plt.title('digit classifier loss')

plt.tight_layout()

Вариационные автокодировщики: теория и рабочий код - 96

Кроме того, давайте выведем сгенерированные изображения и посмотрим, действительно ли модель умеет создавать картинки с рукописными цифрами:

def plot_samples(samples):
    IMAGE_WIDTH = 0.7
    plt.figure(figsize=(IMAGE_WIDTH * num_digits,
                        len(samples) * IMAGE_WIDTH))
    for epoch, images in enumerate(samples):
        for digit, image in enumerate(images):
            plt.subplot(len(samples),
                        num_digits,
                        epoch * num_digits + digit + 1)
            plt.imshow(image.reshape((28, 28)),
                       cmap='Greys_r')
            plt.gca().xaxis.set_visible(False)
            if digit == 0:
                plt.gca().yaxis.set_ticks([])
                plt.ylabel('epoch {}'.format(epoch + 1),
                           verticalalignment='center',
                           horizontalalignment='right',
                           rotation=0,
                           fontsize=14)
            else:
                plt.gca().yaxis.set_visible(False)
                
                
plot_samples(samples)

Вариационные автокодировщики: теория и рабочий код - 97

Заключение

Приятно видеть, что простая сеть прямого распространения (без причудливых свёрток) генерирует красивые изображения всего за 20 эпох. Модель довольно быстро научилась использовать особые измерения для цифр: в 9-й эпохе мы уже видим последовательность цифр, которую пытались сгенерировать.

Каждая эпоха использовала разные случайные значения для других измерений, поэтому стиль отличается между эпохами, но похож внутри них: по крайней мере, внутри некоторых. Например, в 18-й все цифры более жирные, по сравнению с 20-й.

Примечания

Cтатья основана на моём опыте и следующих источниках:

Автор: m1rko

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js