Всем привет. В прошлом посте я рассказывал про некоторые базовые методы классификации. Сегодня, в силу специфики последней домашки, пост будет не столько про сами методы, сколько про обработку данных и анализ полученных моделей.
Задача
Данные были предоставлены факультетом статистики Мюнхенского университета. Вот здесь можно взять сам датасет, а также само описание данных (названия полей даны на немецком). В данных собраны заявки на предоставление кредита, где каждая заявка описывается 20 переменными. Помимо этого, каждой заявке соответствует, выдали ли заявителю кредит, или нет. Вот здесь можно подробно посмотреть, что какая из переменных означает.
Нашей задачей стояло построить модель, которая предсказывала бы решение, которое будет вынесено по тому или иному заявителю.

Тестовых данных и системы для проверки наших моделей, как это, например сделано в MNIST, увы, не было. В связи с этим, у нас был некоторый простор для фантазии в плане валидации наших моделей.
Пре-процессинг данных
Давайте для начала взглянем на сами данные. На следующем графике показаны гистограммы распределений всех имеющихся в нашем наличии переменных. Порядок появления переменных специально изменен, для наглядности.
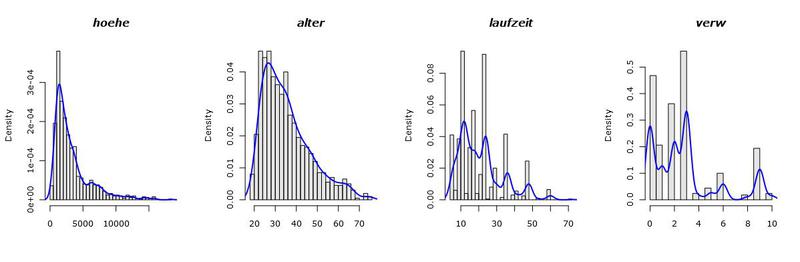
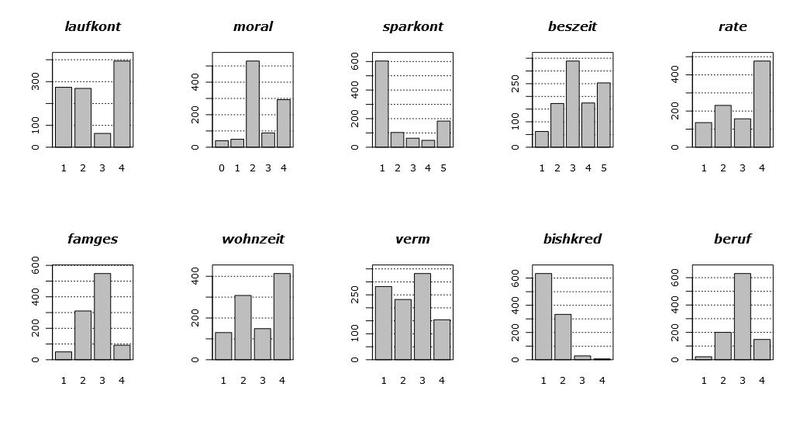
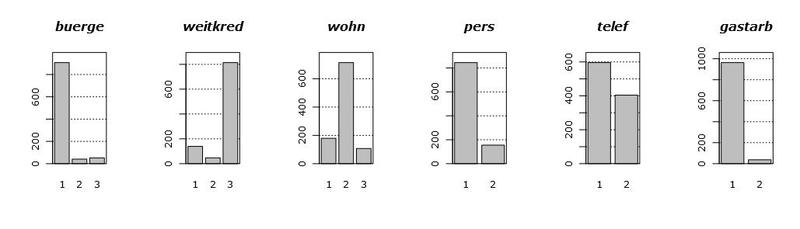
Посмотрев на эти графики, можно сделать несколько выводов. Во-первых большинство переменных у нас фактически категориальные, тоесть они принимают всего пару (пар) значений. Во-вторых, есть всего две (ну, может быть три) условно-непрерывные переменные, а именно hoehe и alter. В-третьих, выбросов по всей видимости нет.
При работе с непрерывными переменными, вообще говоря, виду их распределения простить можно довольно многое. Например, мультимодальность, когда плотность имеет причудливую холмистую форму, с несколькими вершинами. Что-то похожее можно увидеть на графике плотности переменной laufzeit. Но растянутые хвосты распределений – основная головная боль в построении моделей, так как они очень сильно влияют на их свойства и вид. Выбросы также сильно влияют на качество построенных моделей, но так как нам повезло, и их у нас нет, то про выбросы я расскажу как-нибудь в следующий раз.
Возвращаясь к нашим хвостам, у переменных hoehe и alter есть одна особенность: они не нормальные. Тоесть, они очень похожи на логнормальные, ввиду сильного правого хвоста. Учитывая все выше сказанное, у нас есть некоторые основания эти переменные прологарифмировать, чтобы эти хвосты поджать.
В чем сила, брат? Или кто все эти люди переменные?
Зачастую, при проведении анализа, некоторые переменные оказываются ненужными. То есть, вот ну совсем. Это означает, что если выкинуть их из анализа, то при решении нашей задачи, мы даже в худшем случае почти ничего не потеряем. В нашем случае кредитного скоринга, под потерям мы понимаем чуть уменьшившуюся точность классификации.
Это то, что будет в худшем случае. Однако практика показывает, что при тщательном отборе переменных, в народе известном как feature selection, в точности можно даже выиграть. Незначащие переменные вносят в модель исключительно шум, почти никак не влия на результат. И когда их собирается достаточно много, приходится отделять зерна от плевел.
На практике эта задача возникает из-за того, что к моменту сбора данных, экспертам еще не известно, какие переменные будут наиболее значимы в анализе. При этом, во время самого эксперимента и сбора данных, никто не мешает экспериментаторам собрать все переменные, которые вообще можно собрать. Мол, соберем все что есть, а аналитики уже как-нибудь сами разберутся.
Резать переменные надо с умом. Если просто резать данные по частоте появления признака, например в случае переменной gastarb, то мы не можем заведомо гарантировать, что не выкинем весьма значимый признак. В каких-нибудь текстовых или биологических данных, эта проблема еще более явна, так как там вообще очень редко какие переменные принимают отличные от нуля значения.
Проблема с отбором признаков состоит в том, что для каждой модели, натягиваемой на данные, критерий отбора признаков будет свой, специально под эту модель построенный. Например, для линейных моделей используются t-статистики на значимость коэффициентов, а для Random Forest – относительная значимость переменных в каскаде деревьев. А иногда feature selection вообще может быть явно встроен в модель.
Для простоты, рассмотрим только значимость переменных в линейной модели. Мы просто построим обобщенную линейную модель, GLM. Так как наша целевая переменная – метка класса, то следовательно, имеет (условно) биномиальное распределение. Используя функцию glm в R, построим эту модель и заглянем ей под капот, вызвав для нее summary. В результате мы получим следующую табличку:
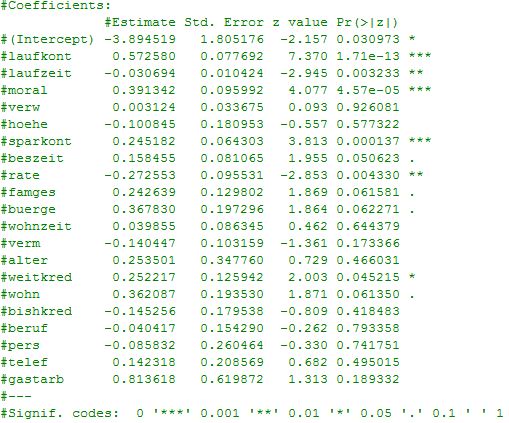
Нас интересует самый последний столбец. Этот столбец означает вероятность того, что наш коэффициент равен нулю, то есть не играет роли в итоговой модели. Звездочками здесь помечены относительные значимости коэффициентов. Из таблицы мы видим, что, вообще говоря, мы можем безжалостно выпилить почти все переменные, кроме laufkont, laufzeit, moral и sparkont (intercept это параметр сдвига, он нам тоже нужен). Мы их выбрали на основании полученной статистики, то есть это те переменные для которых статистика «на вылет» меньше или равна 0.01.
Если закрыть глаза на валидацию модели, считая что линейная модель не переподгонит наши данные, можно проверить верность нашей гипотезы. А именно, протестируем точность двух моделей на всех данных: модель с 4 переменными и модель с 20-тью. Для 20 переменных, точность классисификации составит 77.1%, в то время как для модели с 4 переменными, 76.1%. Как видно, не очень-то и жалко.
Занятно, что прологарифмировнные нами переменные, никак не влияют на модель. Будучи ни разу не прологарифмированными, а также прологарифмированными двжады, по значимости не дотянули даже до 0.1.
Анализ
Сами классисификаторы мы решили строить на Python, с использованием Scikit. В анализе мы решили использовать все основные классификаторы, которые предоставляет scikit, както поигравшись с их гиперпараметрами. Вот список того, что было запущено:
- GLM
- SVM
- kNN
- Random Forest
- Gradient Boosting
Поскольку возможности протестировать выходные данные явным образом у нас не было, мы воспользовались метод кросс-валидации. В качестве числа fold’ов мы брали 10. В качества результата мы выводим среднее значение точности классификации со всех 10 fold-ов.
Реализация весьма прозрачна.
from sklearn.externals import joblib
from sklearn import cross_validation
from sklearn import svm
from sklearn import neighbors
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
import numpy as np
def avg(x):
s = 0
for t in x:
s += t
return (s/len(x))*100
dataset = joblib.load('kredit.pkl') #сюда были свалены данные, полученные после препроцессинга
target = [x[0] for x in dataset]
target = np.array(target)
train = [x[1:] for x in dataset]
numcv = 10 #количество фолдов
glm = LogisticRegression(penalty='l2', tol=1)
scores = cross_validation.cross_val_score(glm, train, target, cv = numcv)
print("Logistic Regression with L1 metric - " + ' avg = ' + ('%2.1f'%avg(scores)))
linSVM = svm.SVC(kernel='linear', C=1)
scores = cross_validation.cross_val_score(linSVM, train, target, cv = numcv)
print("SVM with linear kernel - " + ' avg = ' + ('%2.1f'%avg(scores)))
poly2SVM = svm.SVC(kernel='poly', degree=2, C=1)
scores = cross_validation.cross_val_score(poly2SVM, train, target, cv = numcv)
print("SVM with polynomial kernel degree 2 - " + ' avg = ' + ('%2.1f' % avg(scores)))
rbfSVM = svm.SVC(kernel='rbf', C=1)
scores = cross_validation.cross_val_score(rbfSVM, train, target, cv = numcv)
print("SVM with rbf kernel - " + ' avg = ' + ('%2.1f'%avg(scores)))
knn = neighbors.KNeighborsClassifier(n_neighbors = 1, weights='uniform')
scores = cross_validation.cross_val_score(knn, train, target, cv = numcv)
print("kNN 1 neighbour - " + ' avg = ' + ('%2.1f'%avg(scores)))
knn = neighbors.KNeighborsClassifier(n_neighbors = 5, weights='uniform')
scores = cross_validation.cross_val_score(knn, train, target, cv = numcv)
print("kNN 5 neighbours - " + ' avg = ' + ('%2.1f'%avg(scores)))
knn = neighbors.KNeighborsClassifier(n_neighbors = 11, weights='uniform')
scores = cross_validation.cross_val_score(knn, train, target, cv = numcv)
print("kNN 11 neighbours - " + ' avg = ' + ('%2.1f'%avg(scores)))
gbm = GradientBoostingClassifier(learning_rate = 0.001, n_estimators = 5000)
scores = cross_validation.cross_val_score(gbm, train, target, cv = numcv)
print("Gradient Boosting 5000 trees, shrinkage 0.001 - " + ' avg = ' + ('%2.1f'%avg(scores)))
gbm = GradientBoostingClassifier(learning_rate = 0.001, n_estimators = 10000)
scores = cross_validation.cross_val_score(gbm, train, target, cv = numcv)
print("Gradient Boosting 10000 trees, shrinkage 0.001 - " + ' avg = ' + ('%2.1f'%avg(scores)))
gbm = GradientBoostingClassifier(learning_rate = 0.001, n_estimators = 15000)
scores = cross_validation.cross_val_score(gbm, train, target, cv = numcv)
print("Gradient Boosting 15000 trees, shrinkage 0.001 - " + ' avg = ' + ('%2.1f'%avg(scores)))
#распараллеливать на несколько ядер он почему-то отказывается
forest = RandomForestClassifier(n_estimators = 10, n_jobs = 1)
scores = cross_validation.cross_val_score(forest, train, target, cv=numcv)
print("Random Forest 10 - " +' avg = ' + ('%2.1f'%avg(scores)))
forest = RandomForestClassifier(n_estimators = 50, n_jobs = 1)
scores = cross_validation.cross_val_score(forest, train, target, cv=numcv)
print("Random Forest 50 - " +' avg = ' + ('%2.1f'%avg(scores)))
forest = RandomForestClassifier(n_estimators = 100, n_jobs = 1)
scores = cross_validation.cross_val_score(forest, train, target, cv=numcv)
print("Random Forest 100 - " +' avg = '+ ('%2.1f'%avg(scores)))
forest = RandomForestClassifier(n_estimators = 200, n_jobs = 1)
scores = cross_validation.cross_val_score(forest, train, target, cv=numcv)
print("Random Forest 200 - " +' avg = ' + ('%2.1f'%avg(scores)))
forest = RandomForestClassifier(n_estimators = 300, n_jobs = 1)
scores = cross_validation.cross_val_score(forest, train, target, cv=numcv)
print("Random Forest 300 - " +' avg = '+ ('%2.1f'%avg(scores)))
forest = RandomForestClassifier(n_estimators = 400, n_jobs = 1)
scores = cross_validation.cross_val_score(forest, train, target, cv=numcv)
print("Random Forest 400 - " +' avg = '+ ('%2.1f'%avg(scores)))
forest = RandomForestClassifier(n_estimators = 500, n_jobs = 1)
scores = cross_validation.cross_val_score(forest, train, target, cv=numcv)
print("Random Forest 500 - " +' avg = '+ ('%2.1f'%avg(scores)))
После того, как мы запустили наш скрипт, мы получили следующие результаты:
| Метод с параметрами | Средняя точность на 4 переменных | Средняя точность на 20 переменных |
|---|---|---|
| Logistic Regression, L1 metric | 75.5 | 75.2 |
| SVM with linear kernel | 73.9 | 74.4 |
| SVM with polynomial kernel | 72.6 | 74.9 |
| SVM with rbf kernel | 74.3 | 74.7 |
| kNN 1 neighbour | 68.8 | 61.4 |
| kNN 5 neighbours | 72.1 | 65.1 |
| kNN 11 neighbours | 72.3 | 68.7 |
| Gradient Boosting 5000 trees shrinkage 0.001 | 75.0 | 77.6 |
| Gradient Boosting 10000 trees shrinkage 0.001 | 73.8 | 77.2 |
| Gradient Boosting 15000 trees shrinkage 0.001 | 73.7 | 76.5 |
| Random Forest 10 | 72.0 | 71.2 |
| Random Forest 50 | 72.1 | 75.5 |
| Random Forest 100 | 71.6 | 75.9 |
| Random Forest 200 | 71.8 | 76.1 |
| Radom Forest 300 | 72.4 | 75.9 |
| Random Forest 400 | 71.9 | 76.7 |
| Random Forest 500 | 72.6 | 76.2 |
Более наглядно, их можно провизуализировать следующим графиком:
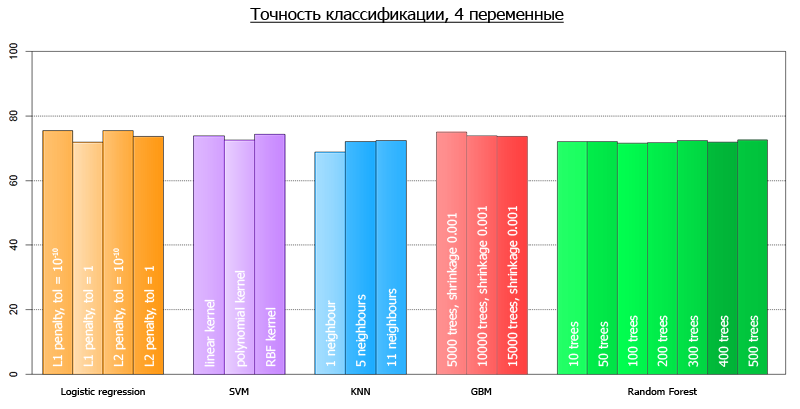
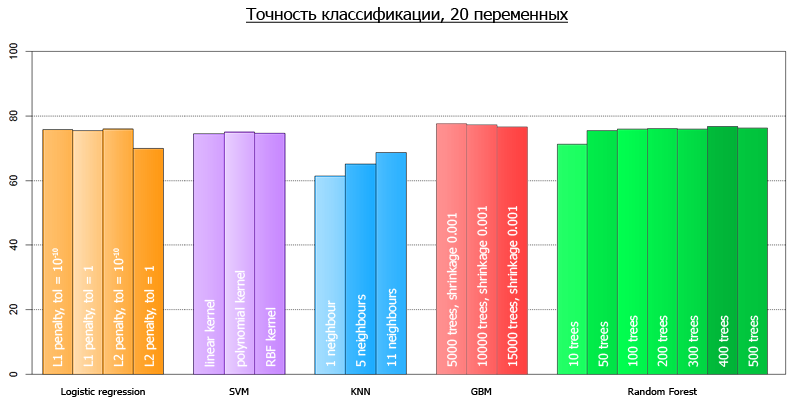
Средняя точность по всем-всем моделям на 4 переменных составляет 72.7
Средняя точность по всем-всем моделям на всех-всех переменных составляет 73.7
Расхождение с предсказанными в начале статьи объясняется тем, что те тесты производились на другом фреймворке.
Выводы
Посмотрев на полученные нами результаты точности моделей, можно сделать пару интересных выводов. Мы построили пачку разных моделей, линейных и нелинейных. А в результате, все эти модели показывают на данных примерно одинаковую точность. То есть, такие модели, как RF и SVM не дали существенных преимуществ в точности в сравнении с линейной моделью. Это скорее всего является следствием того, что исходные данные почти наверняка какой-то линейной зависимостью и были порождены.
Следствием этого будет то, что бессмысленно гнаться на этих данных за точностью сложными массивными методами, типа Random Forest, SVM или GBM. То есть, все, что можно было поймать в этих данных, и так было поймано уже линейной моделью. В противном случае, при наличии явных нелинейных зависимостей в данных, эта разница в точности была бы более значимой.
Это говорит нам о том, что иногда данные не так сложны, как кажутся, и очень быстро можно придти к фактическому максимуму того, что из них можно выжать.
Более того, из сильно сокращенных данных с помощью отбора признаков, наша точность фактически не пострадала. Тоесть наше решение для этих данных оказалось не только простым (дешево-сердито), но и компактным.
За помощь в написании статьи спасибо треку Data Mining от GameChangers, а также Алексею Натёкину.
Автор: LexTalionis






