Можно ли выиграть в азартные игры? Симуляция на языке Python

Привет.

В процессе праздного ничегонеделания возникла идея поизучать разные азартные игры, заодно получше разобраться с тем как это работает. Результаты оказались хотя и в целом очевидными, но достаточно интересными, чтобы поделиться ими с общественностью.

Кому интересны подробности, прошу под кат.

Игральные кости: игра крэпс

Самый наверное, интуитивно простой и понятный вариант — есть кубик с метками от 1 до 6, и вероятность выпадения того или иного числа равна 1/6. Но играть таким способом было бы скучно, поэтому популярны игры с более сложными правилами. Популярной азартной игрой является крэпс, на рисунке выше приведена картинка игрового стола. Как можно видеть, там много всего, но мы не будем вдаваться в глубокие тонкости.

Каждый ход игры состоит из бросания двух кубиков, набранные очки суммируются. Как написано в статье www.vokrugsveta.ru/article/215452 “Правила игры незамысловаты: игрок кидает две кости, и, если сумма очков на них равна 7 или 11, он выигрывает, если 2, 3 или 12 — проигрывает. Когда на кубиках выпадает другая сумма, шутер бросает их до выигрышной или проигрышной комбинаций”.

Посмотрим, сколько можно выиграть таким способом. Для этого необязательно идти в казино, для симуляции игры воспользуемся Python. Напишем функцию для одного броска:

import random

def shoot():
    return random.randint(1,6) + random.randint(1,6)

Напишем функцию симуляции одного хода по вышеописанным правилам.

def move():
    while True:
        val = shoot()
        print "Dice roll:", val
        if val == 7 or val == 11:
            return True
        if val == 2 or val == 3 or val == 12:
            return False

Зададим нашему виртуальному игроку начальную сумму в 100 у.е., и запустим процесс игры. Пусть наш игрок сделает 100 ставок, каждый раз по 1у.е.

money_total = 100
win = 0
loss = 0
for p in range(100):
    bet = 1
    step = move()
    if step is True:
        money_total += bet
        win += 1
    else:
        money_total -= bet
        loss += 1
print "Win", win, "Loss", loss, "Money", money_total

Запускаем симуляцию 100 игр и удивляемся результату, игрок выиграл, причем с заметным отрывом побед от поражений: Win 63, Loss 37, Money 126. Увеличиваем число игр до 1000 и запускаем еще раз, игрок опять выиграл: Win 680, Loss 320, Money 460.

Понятно, что что-то здесь не так — игра, в которой игрок был бы всегда в плюсе, вряд ли была бы популярной в казино, оно бы просто разорилось. Попробуем разобраться.

Интуитивно кажется, что при бросании кубика вероятность выпадения любой грани равновероятна. И это действительно так, но в случае одного кубика. Если кубиков два, то все становится сложнее. К примеру, число 7 может выпасть как 3+4, 2+5, 1+6, а вот число 12 может выпасть только в виде комбинации 6+6.

Построим в Jupyter notebook график выпадения сумм от 1 до 12 для 100 бросков:

from matplotlib import pyplot as plt
%matplotlib inline
y = [ shoot() for v in range(100) ]
plt.hist(y)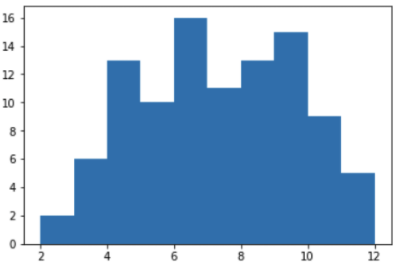

Предположение подтвердилось, и суммы из центра действительно выпадают чаще. Таким образом, числа 7 и 11 действительно выпадают чаще чем 2,3 или 12. И вероятность получить выигрышную комбинацию “7 или 11” действительно выше.

Как такое может быть? Увы, ответ прост — автор процитированной выше статьи просто не разобрался досконально в правилах игры. Текст “правила игры незамысловаты: игрок кидает две кости, и, если сумма очков на них равна 7 или 11, он выигрывает, если 2, 3 или 12 — проигрывает” весьма далек от правды, и правила в крэпс совсем не так незамысловаты как кажутся.

Реальные правила для ставки на pass line оказались несколько сложнее (есть и другие виды ставок, желающие могут разобраться самостоятельно).
Ход-1: Делается бросок. Если выпадает 7 или 11, игрок выигрывает, если 2, 3 или 12, игрок проигрывает. Если выпадает другое число, оно запоминается под названием point.
Ход-2: Делается бросок. Если выпадает 7, то игрок проиграл. Если выпадает point то игрок выиграл. Если выпадают другие числа, ход повторяется (в это время игроки могут также делать ставки на другие числа).

Действительно, все чуть сложнее, чем описывалось в изначальном варианте. Допишем функцию симуляции с учетом более точных правил.

def move():
    point = 0
    while True:
        val = shoot()
        if point == 0:
            # First move
            if val == 7 or val == 11:
                return True
            if val == 2 or val == 3 or val == 12:
                return False
            point = val
        else:
            # 2..N move
            if val == 7:
                return False
            if val == point:
                return True

Результат теперь более похож на правду: за 100 игр игрок выиграл 43 раза, проиграл 57 раз, баланс в конце игры составил 86у.е. от изначальных 100. Интересно и то, что число выигрышей оказалось довольно-таки велико, и составляет лишь немногим менее 50%. Это грамотная стратегия с точки зрения казино — она позволяет поддерживать интерес участника к игре (все время проигрывать было бы неинтересно), но в то же время баланс прибыли казино остается положительным, а баланс денег игрока — соответственно, отрицательным.

Посмотрим подробнее, что получается для симуляции в 100 игр.
— Шанс выиграть на первом шаге выпал примерно в 20 случаях.
— Шанс проиграть сразу на первом шаге выпал в 15 случаях
— В остальных 65 случаях игра продолжается, и тут все хитро: выбор происходит из двух чисел, 7 и point, но как было видно из графика выше, вероятность выпадения “проигрышной” цифры 7 максимальна, что в общем-то и требовалось доказать.

Интересно заметить, что шанс выигрыша в 45% — довольно-таки высок. Так можно ли выиграть? В краткосрочном периоде, да, например, в другой симуляции игроку “повезло”, и он за 100 игр увеличил свой виртуальный капитал со 100 до 112уе.

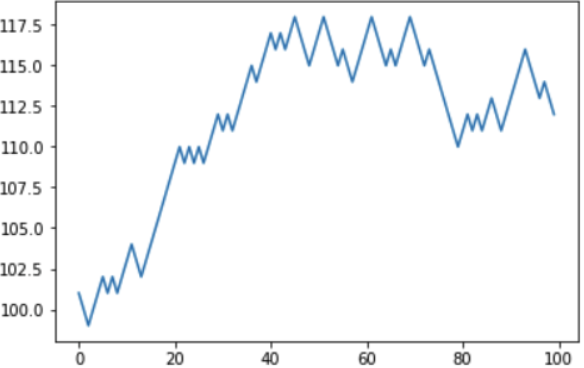
Но уже следующая симуляция показала отрицательный баланс: игрок уменьшил свое состояние со 100 до 88уе, потеряв, кстати, те же самые 12уе, “выигранные” в предыдущий раз.

Если увеличить число итераций до 1000, то можно увидеть как может выглядеть денежный баланс игрока в долгосрочной перспективе:

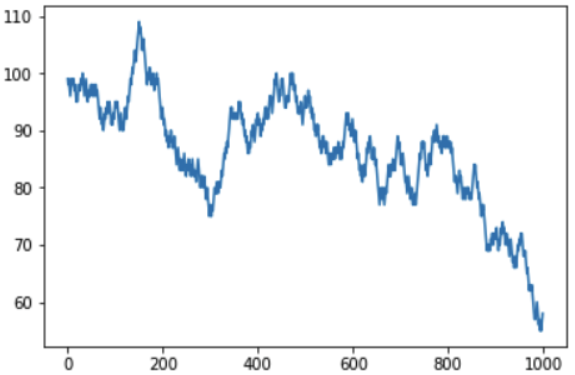
Понятно, что при шансе выигрыша каждой игры менее 50%, результирующая сумма денег на счету игрока будет постепенно уменьшаться, а сумма прибыли казино постепенно увеличиваться. На графике кстати, видны всплески и падения, и может возникнуть резонный вопрос — можно ли их предсказать? Увы нет, т.к. бросания кубика — это независимые друг от друга события, и предыдущие результаты никак не влияют на следующие. Можно еще раз повторить главную мысль — можно выиграть один или даже несколько раз, но в долгосрочном периоде остаться в плюсе у казино невозможно, правила игры составлены так что баланс будет не в пользу игрока.

В игре крэпс есть и другие виды ставок, желающие могут проанализировать их самостоятельно.

Американская рулетка

Следующий популярный вид азартных игр — рулетка, рассмотрим ее американский вариант.

Игровое поле рулетки делится на 38 ячеек: 36 зон с цифрами + 2 зоны “zero” и “double zero”. Брошенный на рулетку шарик очевидно, остановится в одной из зон. Игрок может делать разнообразные ставки, видов которых более 10, рассмотрим некоторые из них.

Черное-красное (или чет-нечет)
Игрок выигрывает, если названная им ставка совпала. Очевидно, что вероятность черного или красного была бы 50/50, если бы не два поля zero — при попадании на них ставка проигрывает. Как и в случае с крэпсом, это делает вероятность выигрыша лишь чуть менее 50% — но этого “чуть” достаточно, чтобы быть в минусе.

Напишем функцию симуляции хода с помощью случайных чисел от 1 до 38, последние 2 цифры будем считать за “зеро”.

def move_roulette1():
    val = random.randint(1,38)
    if val == 37 or val == 38: 
        return False
    return val % 2 != 0

Запустим симуляцию для 100 игр, код тот же самый что и в симуляции крэпса, поменяем только вызов функции.

money_total = 100
win = 0
loss = 0
for p in range(100):
    bet = 1
    step = move_roulette1()
    if step is True:
        money_total += bet
        win += 1
    else:
        money_total -= bet
        loss += 1
print "Win", win, "Loss", loss, "Money", money_total

Результат: за 100 попыток игрок выиграл 46 раз и проиграл 54 раза. На графике видно, что у игрока были и “взлеты” и “падения”, но итоговый баланс все равно негативный.

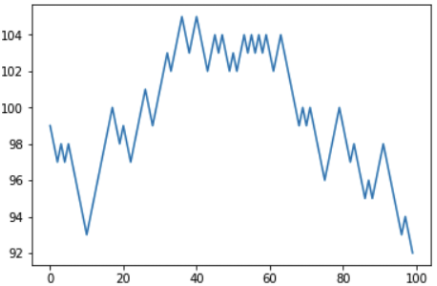
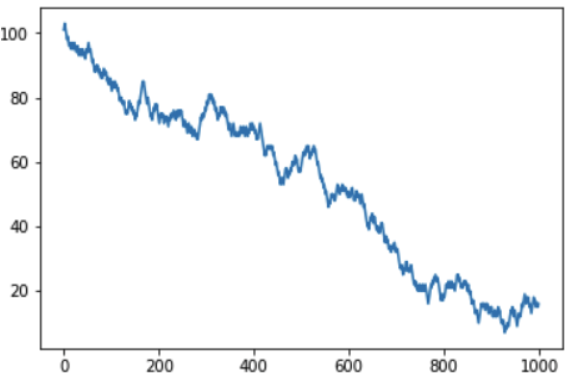
Чем больше мы играем, тем глубже мы уходим в минус, а казино соответственно, в плюс:

Ставка на конкретный номер
Игрок также может поставить на определенный номер, ставка при выигрыше составляет 35:1. Это кажется большим, но нетрудно догадаться, что шанс выпадения определенного номера рулетки 1:38, т.е. опять же, чуть меньше.

Допишем функцию ставки на конкретный номер:

def move_roulette2(num):
    val = random.randint(1,38)
    return val == num

Симуляция, будем считать что игрок ставит на число 10:

money_total = 100
win = 0
loss = 0
for p in range(100):
    bet = 1
    step = move_roulette2(10)
    if step is True:
        money_total += 35*bet
        win += 1
    else:
        money_total -= bet
        loss += 1
print "Win", win, "Loss", loss, "Money", money_total

В результате, игрок выиграл 2 раза и проиграл 98 раз, итоговый баланс -28у.е.

Ставка на два номера
Можно поставить на два номера — шанс выигрыша выше, но зато ставка меньше и составляет 17:1.
Напишем функцию:

def move_roulette3(num1, num2):
    val = random.randint(1,38)
    return val == num1 or val == num2

За 100 попыток нашей симуляции игрок выиграл 3 раза и проиграл 97 раз, баланс составил -46у.е.

Существуют и другие виды ставок, например, на 4 номера с коэффициентом 1:8, желающие могут поэкспериментировать самостоятельно. Как нетрудно догадаться, все коэффициенты рассчитаны так, чтобы игрок оказался в минусе. Кажется заманчивым поставить 1уе на номер, чтобы выиграть целых 35уе. Но сумма выигрыша увеличивается в 35 раз, а шанс выигрыша уменьшается в 38 раз — итоговый баланс все равно будет в пользу казино.

Лото 6 из 45

Следующее, что интересно проверить, это лото. Принцип игры довольно прост — в барабане находятся 45 шаров, выпадают случайным образом 6 из них. Цена билета согласно сайту «Гослото», составляет 100р, а выигрыш зависит от количества угаданных шаров. Примерный порядок сумм выигрыша таков: 2 угаданных шара дают выигрыш в 100р, 3 угаданных шара дают 300р, 4 шара — 3000р, 5 шаров — 300.000р и 6 шаров — суперприз порядка 10.000.000р.

Для начала напишем программу выбрасывания шаров и сравнения результата:

def lottery(values):
    balls = range(1, 45+1)
    b1 = balls.pop(random.randint(0, len(balls)-1))
    b2 = balls.pop(random.randint(0, len(balls)-1))
    b3 = balls.pop(random.randint(0, len(balls)-1))
    b4 = balls.pop(random.randint(0, len(balls)-1))
    b5 = balls.pop(random.randint(0, len(balls)-1))
    b6 = balls.pop(random.randint(0, len(balls)-1))
    s = [b1,b2,b3,b4,b5,b6]

    res = list(set(s) & set(values))
    return len(res)

Из массива balls 6 раз “достается” случайный шар, затем определяется число элементов пересечений двух множеств. Теперь построим график суммарного выигрыша от количества купленных билетов. Для простоты будем считать что игрок ставит на одни и те же числа.

money = [] 
money_total = 0
ticket_price = 100
for p in xrange(N):
    val = lottery([3,7,12,18,33,28])
    if val == 2:
        money_total += 100 
    if val == 3:
        money_total += 300 
    if val == 4:
        money_total += 3000 
    if val == 5:
        money_total += 300000 
    if val == 6:
        money_total += 10000000 
    money.append(money_total)

x = range(0, N)
price = map(lambda x: ticket_price*x, x)

from matplotlib import pyplot as plt
%matplotlib inline
plt.plot(price, money)

Для понимания порядка величин: если купить 100 билетов (суммарная потраченная сумма будет 10.000р), то это дает 14 угаданных “двойных” шаров и один угаданный “тройной”. Суммарный выигрыш составляет около 2000р при потраченных 10.000р.

График выигрыша от потраченной суммы получился практически линейным:

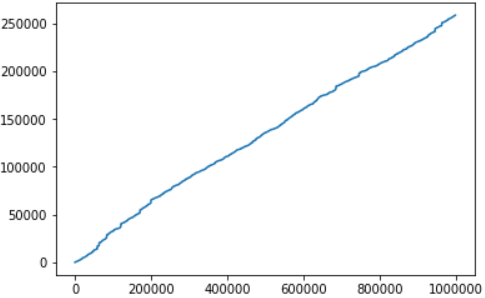
Получается, что если купить билетов на миллион, выигрыш составит 250тыс. “Суперприз” в симуляции так не разу и не выпал, хотя теоретически, он конечно возможен. Кстати, как написано в правилах, призовой фонд составляет 50% с проданных билетов, но “суперприз” выпадает далеко не всегда, так что как и в случае с казино, организаторы разумеется, всегда в выигрыше.

Игровые автоматы

Тоже работают на (псевдо)случайном принципе, «псевдо» т.к. код в них давно программный и чистой механики там почти нет. Общие принципы, описанные выше, для игровых автоматов тоже работают, да и графики скорее всего, не будут отличаться, желающие могут дописать функцию симуляции самостоятельно.

Хорошая статья по конструкции игровых автоматов уже была на geektimes: geektimes.ru/post/290727

Заключение

Наверное эта статья не открыла америку для многих, но на графиках оно в принципе нагляднее. Интереснее оказалось сравить принципиально разный психологический подход к игре. В лотерее выигрыши потенциально велики, но весьма редки. В казино подход обратный — ставки настроены так, что человек будет выигрывать максимально часто. Условно, сделав 10 игр в казино, человек выиграет 4 раза и проиграет 6 раз. Это позволяет игроку не терять интерес к игре, но в любом случае общий баланс остается негативным — человек будет много раз выигрывать, но и чуть-чуть больше проигрывать.

Наверно это и так очевидно, но речь в статье идет только об играх, основанных на случайности, не о покере, картах, шахматах и пр. Может ли существовать «выигрышная стратегия» в таких случайных играх? Очевидно нет, т.к. ни кость, ни шарик, ни лотерейные билеты, не имеют памяти, и их поведение не зависит от предыдущих итераций.

Отвечая на вопрос заголовка статьи — можно ли выиграть в азартные игры? Как показывает, симуляция, в принципе можно, теория вероятности допускает. Но недолго — стоит начать играть 2й, 3й,… Nй раз, как баланс пойдет вниз. В долгосрочной перспективе выиграть у казино невозможно.

Симуляция дело хорошее, но можно попытать счастье на ресурсе "Вулкан Мега" в реальной жизни. Удачных игр.

Автор: DmitrySpb79

Источник