Hessian-Free оптимизация с помощью TensorFlow

Добрый день! Я хочу рассказать про метод оптимизации известный под названием Hessian-Free или Truncated Newton (Усеченный Метод Ньютона) и про его реализацию с помощью библиотеки глубокого обучения — TensorFlow. Он использует преимущества методов оптимизации второго порядка и при этом нет необходимости считать матрицу вторых производных. В данной статье описан сам алгоритм HF, а так же представлена его работа для обучения сети прямого распространения на MNIST и XOR датасетах.

Немного о методах оптимизации

Обучение нейросети включает в себя минимизацию функции ошибки (loss function) по отношению к ее параметрам (weights), которых может быть очень много. Поэтому существуют множество методов оптимизации для решения данной проблемы.

Градиентный спуск (Gradient Descent)

Градиентный спуск — это простейший метод для последовательного нахождения минимума дифференцируемой функции (в случае нейронных сетей это функция стоимости). Имея несколько параметров (веса сети) и дифференцируя по ним функцию получаем вектор частичных производных или вектор градиента:

Градиент всегда указывает по направлению максимального роста функции. Если же мы будем двигаться в противоположную сторону (т.е. ) то со временем придем к минимуму, что нам и требовалось. Простейший алгоритм градиентного спуска:

1. Инициализация: случайно выбираем параметры
2. Вычисляем градиент:
3. Изменяем параметры в сторону отрицательного градиента: , где — некоторый параметр скорости обучения (learning rate)
4. Повторяем предыдущие шаги пока градиент не станет достаточно близок к нулю

Градиентный спуск это довольно простой в реализации и хорошо зарекомендовавший себя метод оптимизации, но есть и минус — он первого порядка, это значит, что берется первая производная по функции стоимости. Это в свою очередь накладывает некоторые ограничения: мы подразумеваем, что наша функция стоимости локально выглядит как плоскость и не учитываем ее кривизну.

Метод Ньютона (Newton's Method)

А что если мы возьмем и будем использовать информацию которую нам дает вторые производные по функции стоимости? Самый известный метод оптимизации с использованием вторых производных — это метод Ньютона. Основная идея этого метода заключается в минимизации квадратичной аппроксимации функции стоимости. Что же это значит? Давайте разберемся.

Возьмем одномерный случай. Предположим у нас есть функция: . Что бы найти точку минимума, надо найти ноль её производной, потому-что мы знаем: находится в минимуме . Аппроксимируем функцию разложением в ряд Тейлора второго порядка:

Мы хотим найти такую , что будет минимумом. Для этого возьмем производную по и приравняем к нулю:

Если квадратичная функция это будет абсолютным минимумом. Если мы хотим найти минимум итеративно, то берем начальный и обновляем его по такому правилу:

Со временем решение сойдется к минимуму.

Рассмотрим многомерный случай. Положим у нас есть многомерная функция тогда:

Где — гессиан (Hessian) или матрица вторых производных. Исходя из этого для обновления параметров имеем такую формулу:

Проблемы с Методом Ньютона

Как мы можем видеть метод Ньютона — это метод второго порядка и будет работать лучше чем обычный градиентный спуск, потому-что вместо того, что бы в каждом шаге двигаться к локальному минимуму он двигается к глобальному минимуму, если мы предполагаем, что функция квадратичная и разложение второго порядка в ряд Тейлора её хорошая аппроксимация.

Но у данного метода есть один большой минус. Для оптимизации функции стоимости надо находить матрицу Гессе или гессиан . Положим — вектор параметров, тогда:

Как можно видеть гессиан это матрица вторых производных размера и что бы ее посчитать потребуется вычислительных операций, что может быть очень критично для сетей у которых сотни или тысячи параметров. По мимо этого для решения задачи оптимизации с помощью метода Ньютона необходимо найти обратную матрицу Гессе , для этого она должна быть положительно определенной для всех .

Положительно определенная матрица.

Матрица размерности называется неотрицательно определенной если она удовлетворяет условию: . Если при этом выполняется строгое неравенство, то матрица называется положительно определенной. Важным свойством таких матриц является их несингулярность, т.е. существование обратной матрицы . Тут нам и приходит на помощь метод под названием Hessian Free оптимизация.

Hessian-Free оптимизация

Основная идея HF оптимизации заключается в том, что за основу мы берем метод Ньютона, но используем более подходящий способ минимизации квадратичной функции. Но для начала введем основные понятия которые понадобятся в дальнейшем.
Пусть — параметры сети, где — матрица весов (weights), вектор смещений (biases), тогда выходом сети назовем: , где — входной вектор. — функция потерь (loss function), — целевое значение. А функцию которую будем минимизировать определим как среднюю от потерь по всем тренировочным примерам (training batch) :

Далее согласно методу Ньютона определим квадратичную функцию, полученную путем разложения в ряд Тейлора второго порядка:

Далее взяв производную по от формулы выше и приравнивая её к нулю получаем:

Что бы найти будем использовать метод сопряженных градиентов (conjugate gradient method).

Метод сопряженных градиентов (conjugate gradient method)

Метод сопряженных градиентов (CG) — это итерационный методя решения систем линейных уравнений типа: .

Краткий алгоритм CG:
Входные данные: , , , — шаг алгоритма CG
Инициализация:

1. — вектор ошибки (residual)
2. — вектор направления поиска (search direction)

Повторяем пока не выполнится условие остановки:

Теперь с помощью метода сопряженных градиентов мы можем решить уравнение (2) и найти , которая будет минимизировать (1). В нашем случае: .
Остановка CG алгоритма. Останавливать метод сопряженных градиентов можно исходя из разных критериев. Мы будем делать это на основе относительного прогресса в оптимизации квадратичной функции :

где — размер «окна» по которому будем считать значение прогресса, . Условием остановки возьмем: .
А теперь можно заметить, что главная особенность HF оптимизации заключается в том, что нам не требуется находить гессиан напрямую, а надо лишь найти результат его произведения на вектор.

Умножение гессиана на вектор

Как уже говорилось ранее прелесть данного метода заключается в том, что у нас нет необходимости считай гессиан напрямую. Надо лишь посчитать результат произведения матрицы вторых производных на вектор. Для этого можно представить как производную от по направлению :

Но использование данной формулы на практике может вызвать ряд проблем связанные с вычислением при достаточно маленьком . Поэтому существует метод точного вычисления произведения матрицы на вектор. Введем дифференциальный оператор . Он обозначает производную некоторой величины , зависящей от , по направлению :

Отсюда видно, что бы посчитать произведение гессиана на вектор надо вычислить:

Некоторые улучшения HF оптимизации

1. Обобщенная матрица Ньютона-Гаусса (generalized Gauss-Newton matrix).
Неопределенность матрицы гессиана является проблемой для оптимизации не выпуклых (non-convex) функций, она может привести к отсутствию нижней границы для квадратичной функции и как следствие невозможность нахождения ее минимума. Эту проблему можно решить множеством способов. Например, введение доверительного интервала будет ограничивать оптимизацию или же дампинг (damping) на основе штрафа, который добавляет положительный полу-определенный (positive semi-definite) компонент к матрице кривизны и делает её положительно определенной.

Основываясь же на практических результатах наилучшим способом решить данную проблему является использование матрицы Ньютона-Гаусса вместо матрицы Гессе:

где — якобиан, — матрица вторых производных от функции потерь .
Для нахождения произведения матрицы на вектор : , сначала найдем произведение якобиана на вектор:

потом вычислим произведение вектора на матрицу и в конце умножим матрицу на .

2. Дампинг (damping).
Стандартный метод Ньютона может плохо оптимизировать сильно нелинейные целевые функции. Причиной этому может быть то, что на начальных стадиях оптимизации она может быть очень большой и агрессивной, так как начальная точка находится далеко от точки минимума. Для решения этой проблемы используется дампинг — метод изменения квадратичной функции или ограничения минимизации таким образом, что новая будет лежать в таких пределах, в которых останется хорошей аппроксимацией .
Регуляризация Тихонова (Tikhonov regularization) или дампинг Тихонова (Tikhonov damping). (Не путать с термином «регуляризация», который обычно используется в контексте машинного обучения) Это самый известный метод дампинга, который добавляет квадратичный штраф к функции :

где , — параметр дампинга. Вычисление производится так:

3. Эвристика Левенберга-Марквардта (Levenberg-Marquardt heuristic).
Для дампинга Тихонова характерно динамическое подстраивание параметра . Изменять будем по правилу Левенберга-Марквардта, который часто используется в контексте LM — метода (метод оптимизации, является альтернативой методу Ньютона). Для использования LM — эвристики необходимо посчитать так называемый коэффициент уменьшения (reduction ratio):

где — номер шага HF алгоритма, — результат работы CG минимизации.
Согласно эвристики Левенберга-Марквардта получаем правило обновления :

4. Начальное условие для алгоритма сопряженных градиентов (preconditioning).
В контексте HF оптимизации у нас есть некоторая обратимая матрица трансформации , с помощью которой мы изменяем таким образом, что и вместо минимизируем . Применение данной особенности в алгоритме CG требует вычисление трансформированного вектора ошибки , где .

Краткий алгоритм PCG (Preconditioned conjugate gradient):
Входные данные: , , , , — шаг алгоритма CG
Инициализация:

1. — вектор ошибки (residual)
2. — решение уравнения
3. — вектор направления поиска (search direction)

Повторяем пока не выполнится условие остановки:

1. 
2. 
3. 
4. — решение уравнения
5. 
6. 
7. 

Выбор матрицы довольно не тривиальная задача. Так же, на практике использование диагональной матрицы (вместо матрицы с полным рангом) показывает довольно хорошие результаты. Один из вариантов выбора матрицы — это использование диагональной матрицы Фишера (Empirical Fisher Diagonal):

5. Инициализация CG — алгоритма.
Хорошей практикой является инициализация начальной , для алгоритма сопряженных градиентов, значением , найденным на предыдущем шаге алгоритма HF. При этом можно использовать некоторую константу распада: . Стоит отметить, что индекс относится к номеру шага алгоритма HF, в свою очередь индекс 0 в относится к начальному шагу алгоритма CG.

Полный алгоритм Hessian-Free оптимизации:
Входные данные: , — параметр дампинга, — шаг итерации алгоритма
Инициализация:

Основной цикл HF оптимизации:

1. Вычисляем матрицу
2. Находим решая задачу оптимизации с помощью CG или PCG.
3. Обновляем параметр дампинга с помощью эвристики Левенберга-Марквардта
4. , — параметр скорости обучения (learning rate)
5. 

Таким образом метод Hessian-Free оптимизации позволяет решать задачи нахождения минимума функции большой размерности. При этом не требуется нахождения матрицы Гессе напрямую.

Реализация HF оптимизации на TensorFlow

Теория это конечно хорошо, но давайте попробуем реализовать данный метод оптимизации на практике и посмотрим, что же из этого выйдет. Для написания HF алгоритма я использовал Python и библиотеку глубокого обучения TensorFlow. После этого, в качестве проверки работоспособности я обучил сеть прямого распространения с несколькими слоями на XOR и MNIST датасетах, используя HF метод для оптимизации.

Реализация (создание графа вычислений TensorFlow) для метода сопряженных градиентов.

  def __conjugate_gradient(self, gradients):
    """ Performs conjugate gradient method to minimze quadratic equation 
    and find best delta of network parameters.
    gradients: list of Tensorflow tensor objects
        Network gradients.
    return: Tensorflow tensor object
        Update operation for delta.
    return: Tensorflow tensor object
        Residual norm, used to prevent numerical errors. 
    return: Tensorflow tensor object
        Delta loss. """

    with tf.name_scope('conjugate_gradient'):
      cg_update_ops = []

      prec = None
      #вычисление матрицы P по формуле (9)
      if self.use_prec:
        if self.prec_loss is None:
          graph = tf.get_default_graph()
          lop = self.loss.op.node_def
          self.prec_loss = graph.get_tensor_by_name(lop.input[0] + ':0')
        batch_size = None
        if self.batch_size is None:
          self.prec_loss = tf.unstack(self.prec_loss)
          batch_size = self.prec_loss.get_shape()[0]
        else:
          self.prec_loss = [tf.gather(self.prec_loss, i)
            for i in range(self.batch_size)]
          batch_size = len(self.prec_loss)
        prec = [[g**2 for g in tf.gradients(tf.gather(self.prec_loss, i),
          self.W)] for i in range(batch_size)]
        prec = [(sum(tensor) + self.damping)**(-0.75)
          for tensor in np.transpose(np.array(prec))]
      #основной алгоритм сопряженных градиентов
      Ax = None
      if self.use_gnm:
        Ax = self.__Gv(self.cg_delta)
      else:
        Ax = self.__Hv(gradients, self.cg_delta)

      b = [-grad for grad in gradients]
      bAx = [b - Ax for b, Ax  in zip(b, Ax)]

      condition = tf.equal(self.cg_step, 0)
      r = [tf.cond(condition, lambda: tf.assign(r,  bax),
        lambda: r) for r, bax  in zip(self.residuals, bAx)]

      d = None
      if self.use_prec:
        d = [tf.cond(condition, lambda: tf.assign(d, p * r), 
          lambda: d) for  p, d, r in zip(prec, self.directions, r)]
      else:
        d = [tf.cond(condition, lambda: tf.assign(d, r), 
          lambda: d) for  d, r in zip(self.directions, r)]

      Ad = None
      if self.use_gnm:
        Ad = self.__Gv(d)
      else:
        Ad = self.__Hv(gradients, d)

      residual_norm = tf.reduce_sum([tf.reduce_sum(r**2) for r in r])

      alpha = tf.reduce_sum([tf.reduce_sum(d * ad) for d, ad in zip(d, Ad)])
      alpha = residual_norm / alpha

      if self.use_prec:
        beta = tf.reduce_sum([tf.reduce_sum(p * (r - alpha * ad)**2) 
          for r, ad, p in zip(r, Ad, prec)])
      else:
        beta = tf.reduce_sum([tf.reduce_sum((r - alpha * ad)**2) for r, ad 
          in zip(r, Ad)])

      self.beta = beta
      beta = beta / residual_norm

      for i, delta  in reversed(list(enumerate(self.cg_delta))):
        update_delta = tf.assign(delta, delta + alpha * d[i],
          name='update_delta')
        update_residual = tf.assign(self.residuals[i], r[i] - alpha * Ad[i],
          name='update_residual')
        p = 1.0
        if self.use_prec:
          p = prec[i]
        update_direction = tf.assign(self.directions[i],
          p * (r[i] - alpha * Ad[i]) + beta * d[i], name='update_direction')
        cg_update_ops.append(update_delta)
        cg_update_ops.append(update_residual)
        cg_update_ops.append(update_direction)

      with tf.control_dependencies(cg_update_ops):
        cg_update_ops.append(tf.assign_add(self.cg_step, 1))
      cg_op = tf.group(*cg_update_ops)

    dl = tf.reduce_sum([tf.reduce_sum(0.5*(delta*ax) + grad*delta)
      for delta, grad, ax in zip(self.cg_delta, gradients, Ax)])

    return cg_op, residual_norm, dl

Код для вычисления матрицы для нахождения начального условия (preconditioning) приведен ниже. При этом, так как Tensorflow суммирует результат вычисления градиентов по всему множеству подаваемых примеров обучения, пришлось немного поизвращаться, что бы получить градиент отдельно для каждого примера, что сказалось на численной стабильности решения. Поэтому использование preconditioning возможно, как говорится, на свой страх и риск.

 prec = [[g**2 for g in tf.gradients(tf.gather(self.prec_loss, i),
   self.W)] for i in range(batch_size)]

Вычисление произведения гессиана на вектор (4). При этом используется дампинг Тихонова (6).

  def __Hv(self, grads, vec):
    """ Computes Hessian vector product.
    grads: list of Tensorflow tensor objects
        Network gradients.
    vec: list of Tensorflow tensor objects
        Vector that is multiplied by the Hessian.
    return: list of Tensorflow tensor objects
        Result of multiplying Hessian by vec. """

    grad_v = [tf.reduce_sum(g * v) for g, v in zip(grads, vec)]
    Hv = tf.gradients(grad_v, self.W, stop_gradients=vec)
    Hv = [hv + self.damp_pl * v for hv, v in zip(Hv, vec)]

    return Hv

Когда же я захотел использовать обобщенную матрицу Ньютона-Гаусса (5) я натолкнулся на небольшую проблему. А именно, TensorFlow не умеет считать произведение Якобиана на вектор как это делает другой фреймворк для глубокого обучения Theano (в Theano есть функция Rop специально предназначенная для этого). Пришлось делать аналог операции в TensorFlow.

  def __Rop(self, f, x, vec):
    """ Computes Jacobian vector product.
    f: Tensorflow tensor object
        Objective function.
    x: list of Tensorflow tensor objects
        Parameters with respect to which computes Jacobian matrix.
    vec: list of Tensorflow tensor objects
        Vector that is multiplied by the Jacobian.
    return: list of Tensorflow tensor objects
        Result of multiplying Jacobian (df/dx) by vec. """

    r = None
    if self.batch_size is None:
      try:
        r = [tf.reduce_sum([tf.reduce_sum(v * tf.gradients(f, x)[i])
             for i, v in enumerate(vec)])
             for f in tf.unstack(f)]
      except ValueError:
        assert False, clr.FAIL + clr.BOLD + 'Batch size is None, but used '
          'dynamic shape for network input, set proper batch_size in '
          'HFOptimizer initialization' + clr.ENDC
    else:
      r = [tf.reduce_sum([tf.reduce_sum(v * tf.gradients(tf.gather(f, i), x)[j]) 
           for j, v in enumerate(vec)])
           for i in range(self.batch_size)]

    assert r is not None, clr.FAIL + clr.BOLD +
      'Something went wrong in Rop computation' + clr.ENDC

    return r

И потом уже реализовывать произведение обобщенной матрицы Ньютона-Гаусса на вектор.

  def __Gv(self, vec):
    """ Computes the product G by vec = JHJv (G is the Gauss-Newton matrix).
    vec: list of Tensorflow tensor objects
        Vector that is multiplied by the Gauss-Newton matrix.
    return: list of Tensorflow tensor objects
        Result of multiplying Gauss-Newton matrix by vec. """

    Jv = self.__Rop(self.output, self.W, vec)
    Jv = tf.reshape(tf.stack(Jv), [-1, 1])
    HJv = tf.gradients(tf.matmul(tf.transpose(tf.gradients(self.loss,
      self.output)[0]), Jv), self.output, stop_gradients=Jv)[0]
    JHJv = tf.gradients(tf.matmul(tf.transpose(HJv), self.output), self.W,
      stop_gradients=HJv)
    JHJv = [gv + self.damp_pl * v for gv, v in zip(JHJv, vec)]

    return JHJv

Функция основного процесса обучения представлена ниже. Сначала производится минимизация квадратичной функции с помощью CG/PCG, потом происходит уже основное обновление весов сети. Так же подстраивается параметр дампинга на основе эвристики Левенберга-Марквардта.

  def minimize(self, feed_dict, debug_print=False):
    """ Performs main training operations.
    feed_dict: dictionary
        Input training batch.
    debug_print: bool
        If True prints CG iteration number. """

    self.sess.run(tf.assign(self.cg_step, 0))
    feed_dict.update({self.damp_pl:self.damping})

    if self.adjust_damping:
      loss_before_cg = self.sess.run(self.loss, feed_dict)

    dl_track = [self.sess.run(self.ops['dl'], feed_dict)]
    self.sess.run(self.ops['set_delta_0'])

    for i in range(self.cg_max_iters):
      if debug_print:
        d_info = clr.OKGREEN + 'r[CG iteration: {}]'.format(i) + clr.ENDC
        sys.stdout.write(d_info)
        sys.stdout.flush()

      k = max(self.gap, i // self.gap)

      rn = self.sess.run(self.ops['res_norm'], feed_dict)
      #ранняя остановка для предотвращения численной ошибки
      if rn < self.cg_num_err:
        break

      self.sess.run(self.ops['cg_update'], feed_dict)
      dl_track.append(self.sess.run(self.ops['dl'], feed_dict))

      #ранняя остановка алгоритма, основываясь на формуле (3)
      if i > k:
        stop = (dl_track[i+1] - dl_track[i+1-k]) / dl_track[i+1]
        if not np.isnan(stop) and stop < 1e-4:
          break

    if debug_print:
      sys.stdout.write('n')
      sys.stdout.flush()

    if self.adjust_damping:
      feed_dict.update({self.damp_pl:0})
      dl = self.sess.run(self.ops['dl'], feed_dict)
      feed_dict.update({self.damp_pl:self.damping})

    self.sess.run(self.ops['train'], feed_dict)

    if self.adjust_damping:
      loss_after_cg = self.sess.run(self.loss, feed_dict)
      #коэффициент уменьшения (7)
      reduction_ratio = (loss_after_cg - loss_before_cg) / dl

      #эвристика Левенберга-Марквардта (8)
      if reduction_ratio < 0.25 and self.damping > self.damp_num_err:
        self.damping *= 1.5
      elif reduction_ratio > 0.75 and self.damping > self.damp_num_err:
        self.damping /= 1.5

Тестирование работы HF оптимизации

Протестируем написанный HF оптимизатор, для этого будем использовать простой пример c XOR датасетом и более сложный с MNIST датасетом. Для того, что бы посмотреть результаты обучения и визуализировать некоторую информацию воспользуемся TesnorBoard. Хочется так же заметить, что получился довольно сложный граф вычислений TensorFlow.

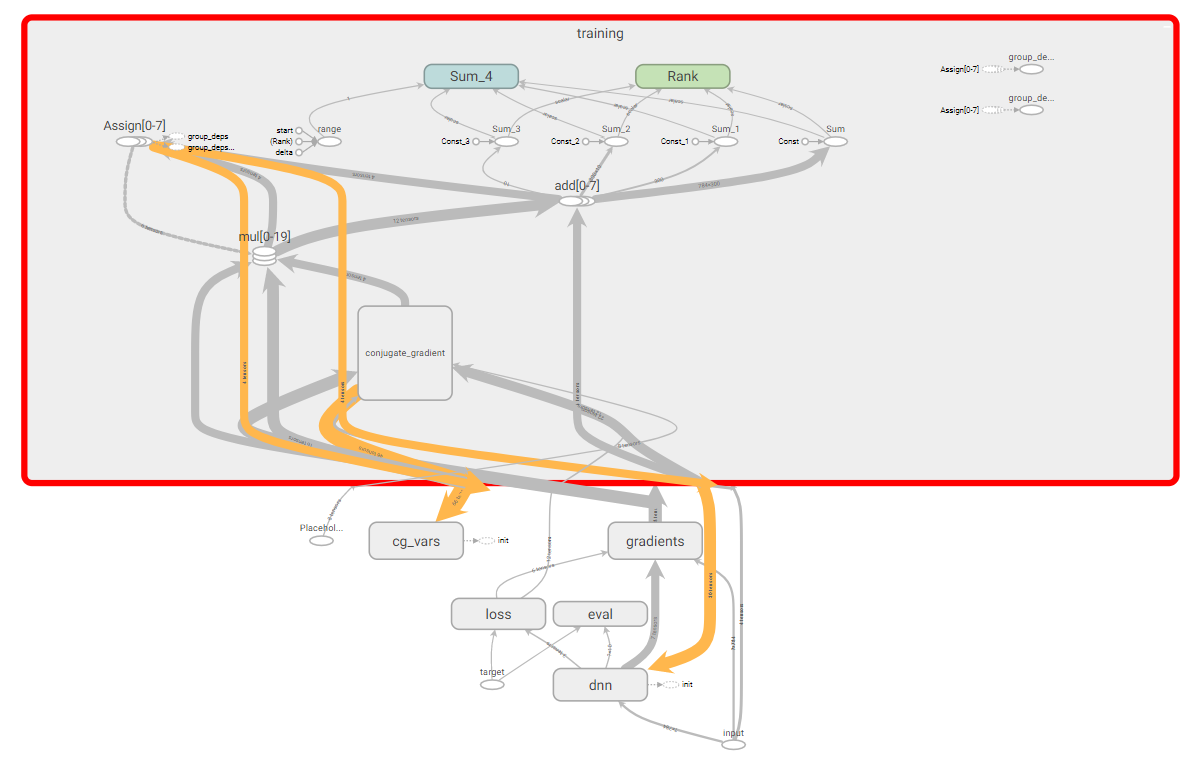
Граф вычислений TensorFlow.

Архитектура и обучение сети на XOR датасете.
Создадим простую сеть размером: 2 входных нейрона, 2 скрытых и 1 выходной. В качестве функции активации будем использовать сигмоиду. В качестве функции потерь используем log-loss.

  #определение функции потерь
  """ Log-loss cost function """
  loss = tf.reduce_mean(( (y * tf.log(out)) + 
    ((1 - y) * tf.log(1.0 - out)) ) * -1, name='log_loss')

  #XOR датасет
  XOR_X = [[0,0],[0,1],[1,0],[1,1]]
  XOR_Y = [[0],[1],[1],[0]]
  
  #создание оптимизатора
  sess = tf.Session()
  hf_optimizer = HFOptimizer(sess, loss, y_out, 
    dtype=tf.float64, use_gauss_newton_matrix=True)

  init = tf.initialize_all_variables()
  sess.run(init)

  #цикл тренировки
  max_epoches = 100
  print('Begin Training')
  for i in range(max_epoches):
    feed_dict = {x: XOR_X, y: XOR_Y}
    hf_optimizer.minimize(feed_dict=feed_dict)
    if i % 10 == 0:
      print('Epoch:', i, 'cost:', sess.run(loss, feed_dict=feed_dict))
      print('Hypothesis ', sess.run(out, feed_dict=feed_dict))

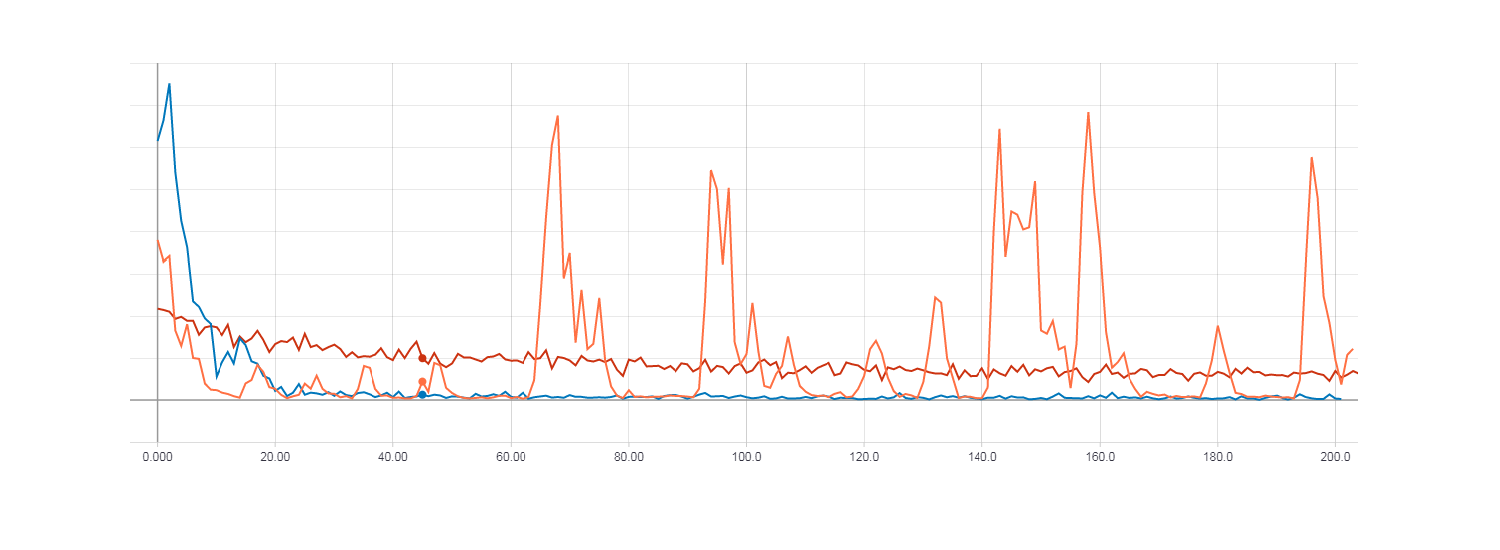
Теперь сравним результаты обучения с использованием HF оптимизации (с матрицей Гессе), HF оптимизации (с матрицей Ньютона-Гаусса) и обычным градиентным спуском с параметром скорости обучения равным 0.01. Количество итераций равно 100.

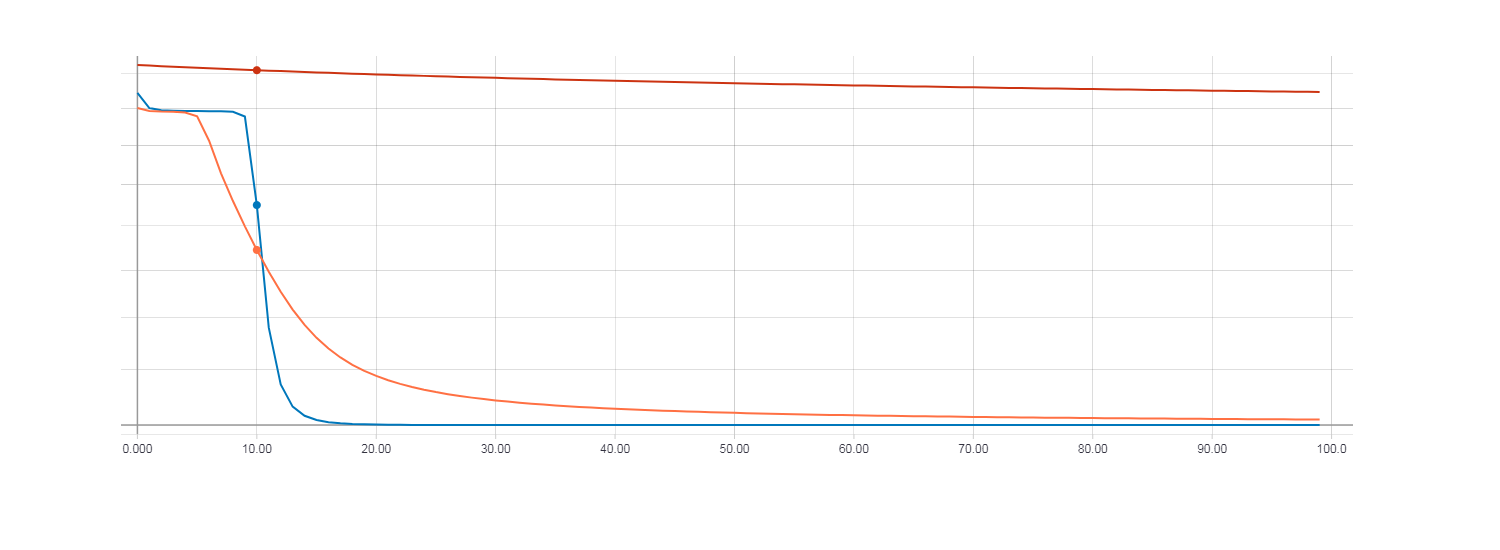
Loss для градиентного спуска (красная линия). Loss для HF оптимизации с матрицей Гессе (оранжевая линия). Loss для HF оптимизации с матрицей Ньютона-Гаусса (синяя линия).

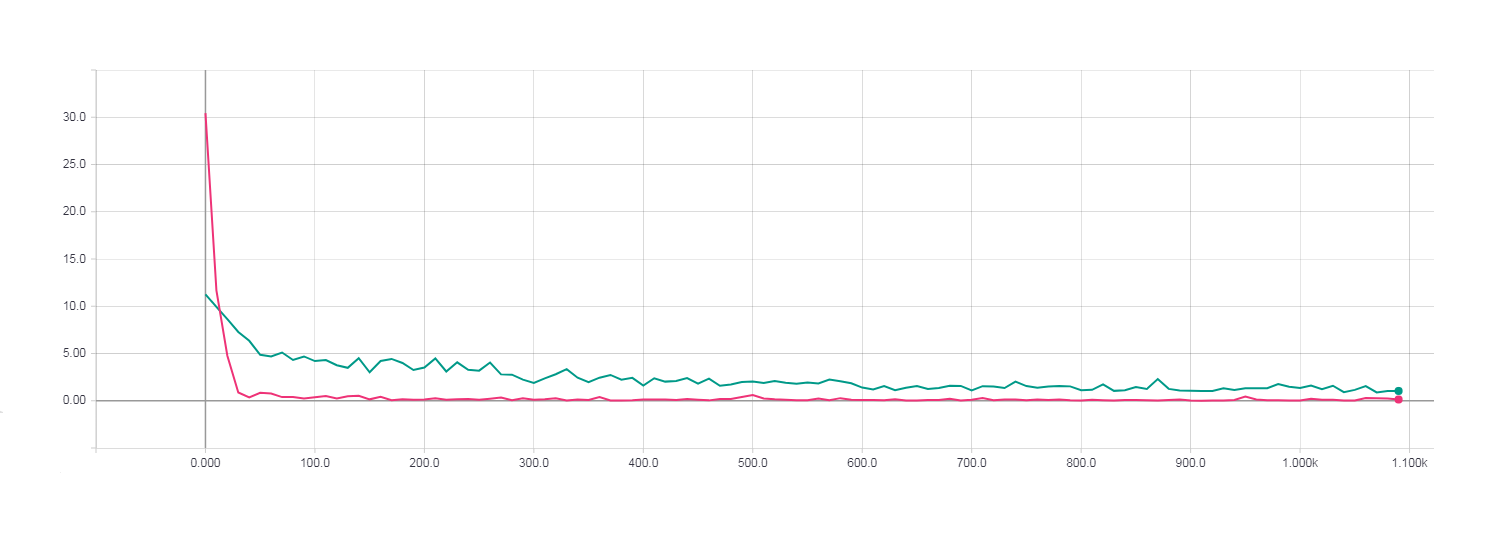
При этом видно что быстрее всего сходится HF оптимизация с использованием матрицы Ньютона-Гаусса, для градиентного же спуска 100 итерации оказалось очень мало. Для того, что бы функция потерь при градиентном спуске была сопоставима с HF оптимизацией потребовалось около 100000 итераций.

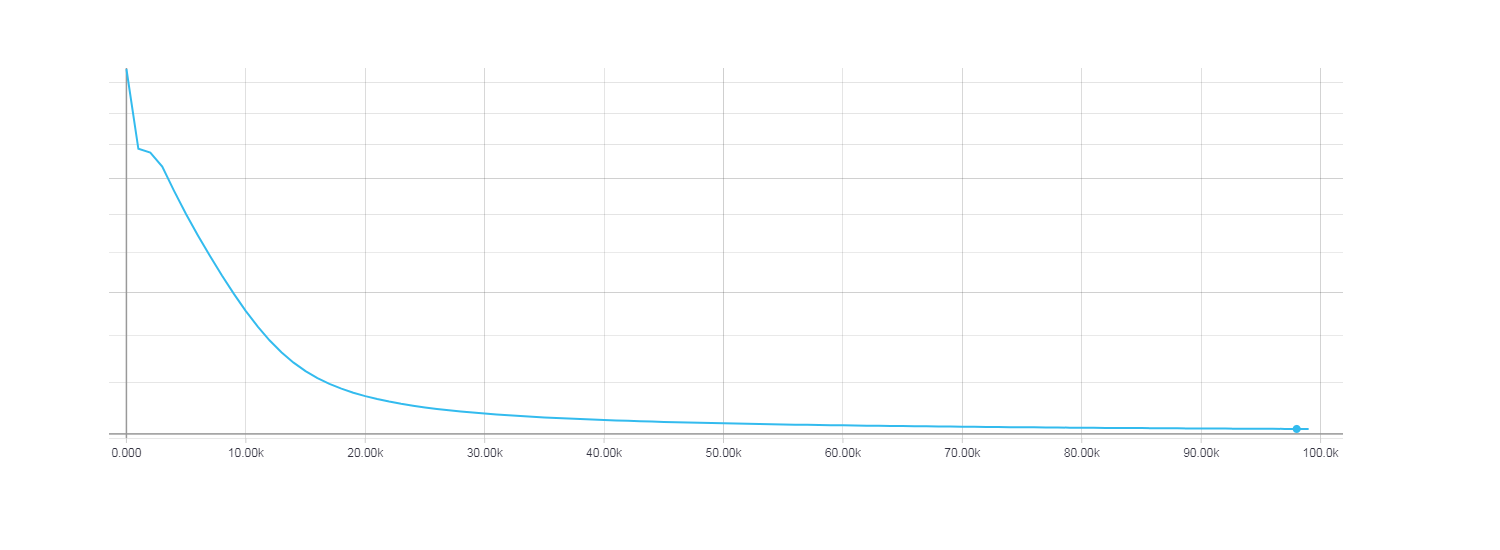
Loss для градиентного спуска, 100000 итераций.

Архитектура и обучение сети на MNIST датасете.
Для решения задачи распознавания рукописных чисел создадим сеть размером: 784 входных нейрона, 300 скрытых и 10 выходных. В качестве функции потерь будем использовать кросс-энтропию. Размер мини батча подаваемого в ходе обучения равен 50-ти.

  with tf.name_scope('loss'):
    one_hot = tf.one_hot(t, n_outputs, dtype=tf.float64)
    xentropy = tf.nn.softmax_cross_entropy_with_logits(labels=one_hot, logits=y_out)
    loss = tf.reduce_mean(xentropy, name="loss")

  with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(tf.cast(y_out, tf.float32), t, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float64))

  n_epochs = 10
  batch_size = 50

  with tf.Session() as sess:
    """ Initializing hessian free optimizer """
    hf_optimizer = HFOptimizer(sess, loss, y_out, dtype=tf.float64, batch_size=batch_size, 
      use_gauss_newton_matrix=True)
    init = tf.global_variables_initializer()
    init.run()
    #основной процесс обучения
    for epoch in range(n_epochs):
      n_batches = mnist.train.num_examples // batch_size
      for iteration in range(n_batches):
        x_batch, t_batch = mnist.train.next_batch(batch_size)
        hf_optimizer.minimize({x: x_batch, t: t_batch})
        if iteration%10==0:
          print('Batch:', iteration, '/', n_batches)
          acc_train = accuracy.eval(feed_dict={x: x_batch, t: t_batch})
          acc_test = accuracy.eval(feed_dict={x: mnist.test.images,
                        t: mnist.test.labels})
          print('Loss:', sess.run(loss, {x: x_batch, t: t_batch}))
          print('Target', t_batch[0])
          print('Out:', sess.run(y_out_sm, {x: x_batch, t: t_batch})[0])
          print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)

      acc_train = accuracy.eval(feed_dict={x: x_batch, t: t_batch})
      acc_test = accuracy.eval(feed_dict={x: mnist.test.images,
                        t: mnist.test.labels})
      print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)

Так же как и в случае с XOR сравним результаты обучения с использованием HF оптимизации (с матрицей Гессе), HF оптимизации (с матрицей Ньютона-Гаусса) и обычным градиентным спуском с параметром скорости обучения равным 0.01. Количество итераций равно 200, т.е. если размер мини батча равен 50, то 200 — это не полная эпоха (не все примеры из обучающей выборки использованы). Я это сделал для того, что бы быстрее все протестировать, но даже из этого видна общая тенденция.

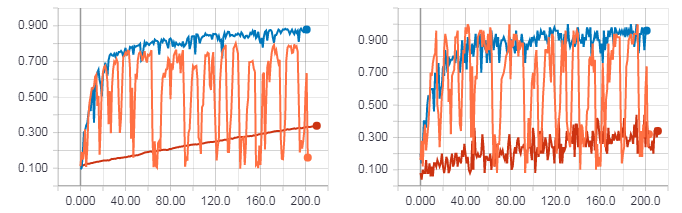
Рисунок слева точность для тестовой выборки. Рисунок справа точность для тренировочной выборки. Точность для градиентного спуска (красная линия). Точность для HF оптимизации с матрицей Гессе (оранжевая линия). Точность для HF оптимизации с матрицей Ньютона-Гаусса (синяя линия).

Loss для градиентного спуска (красная линия). Loss для HF оптимизации с матрицей Гессе (оранжевая линия). Loss для HF оптимизации с матрицей Ньютона-Гаусса (синяя линия).

Как можно заметить из рисунков выше HF оптимизация с матрицей Гессе ведет себя не очень стабильно, но в итоге все равно будет сходиться при обучении с несколькими эпохами. Наилучший результат же показывает HF оптимизация с матрицей Ньютона-Гаусса.

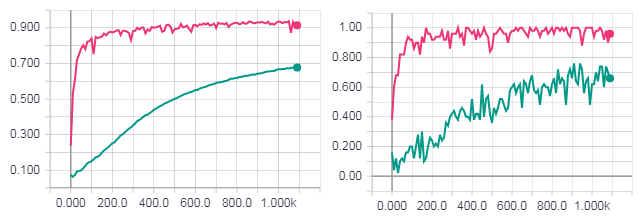
Одна полная эпоха обучения. Рисунок слева точность для тестовой выборки. Рисунок справа точность для тренировочной выборки. Точность для градиентного спуска (бирюзовая линия). Loss для HF оптимизации с матрицей Ньютона-Гаусса (розовая линия).

Одна полная эпоха обучения. Loss для градиентного спуска (бирюзовая линия). Loss для HF оптимизации с матрицей Ньютона-Гаусса (розовая линия).

При использовании метода сопряженных градиентов с начальным условием для алгоритма сопряженных градиентов (preconditioning) сами вычисления значительно замедлились и сходились не быстрее чем при обычном CG.

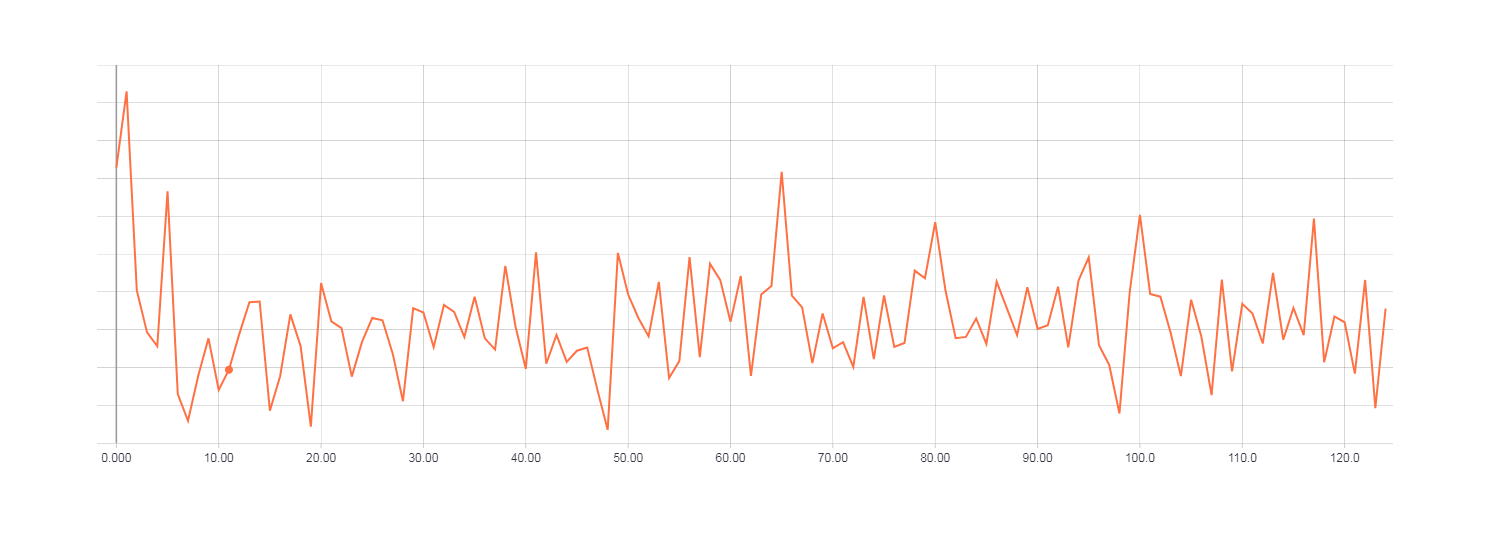
Loss для HF оптимизации с использованием PCG алгоритма.

Из всех этих графиков можно заметить, что наилучший результат показала HF оптимизация с использованием матрицы Ньютона-Гаусса и стандартного метод сопряженных градиентов.
Полный код можно посмотреть на GitHub.

Итоги

В итоге была создана реализация HF алгоритма на Python с помощью библиотеки TensorFlow. В ходе создания я столкнулся с некоторыми проблемами при реализации основных особенностей алгоритма, а именно: поддержки матрицы Ньютона-Гаусса и preconditioning-а. Связано это было с тем, что все таки TensorFlow не такая гибкая библиотека как хотелось бы и не сильно предназначена для исследований. Для экспериментальных целей все таки лучше использовать Theano, так как она дает большую свободу. Но я изначально решил для себя сделать все это с помощью TensorFlow. Работа программы была протестирована и можно было увидеть, что наилучшие результаты дает HF алгоритм с использованием матрицы Ньютона-Гаусса. Использование же начального условия для алгоритма сопряженных градиентов (preconditioning) давало не стабильные численные результаты и сильно замедляло вычисления, но как мне кажется, это связано с особенностью именно TensorFlow (для реализации preconditioning пришлось сильно извращаться).

Источники

В данной статье теоретические аспекты Hessian — Free оптимизации описаны довольно кратко, что бы можно было понять основную суть алгоритмов. Если же необходимо более подробное описание материала, то ниже привожу источники откуда я брал основную теоретическую информацию, на основе которой сделал Python реализацию HF метода.

1) Training Deep and Recurrent Networks with Hessian-Free Optimization (James Martens and Ilya Sutskever, University of Toronto) — полное описание HF — оптимизации.
2) Deep learning via Hessian-free optimization (James Martens, University of Toronto) — статья с результатами использования HF — оптимизации.
3) Fast Exact Multiplication by the Hessian (Barak A. Pearlmutter, Siemens Corporate Research) — подробное описание умножения матрицы Гессе на вектор.
4) An introduction to the Conjugate Gradient Method without the Agonizing Pain (Jonathan Richard Shewchuk, Carnegie Mellon University) — подробное описание метода сопряженных градиентов.

Автор: M00nL1ght

Источник