Введение
Тепловыделяющий элемент (ТВЭЛ) — главный конструктивный элемент активной зоны гетерогенного ядерного реактора, содержащий ядерное топливо [1].
В ТВЭЛах происходит деление тяжелых ядер урана 235 или плутония 239, сопровождающееся выделением тепловой энергии, которая затем передаётся теплоносителю.
ТВЭЛ должен обеспечить отвод тепла от топлива к теплоносителю и препятствовать распространению радиоактивных продуктов из топлива в теплоноситель.
Поэтому расчёт температурных полей в ТВЭЛах является важной задачей проектирования ядерного реактора.
В данной публикации приведена методика расчета распределения температуры для стержневого осесимметричного твэла, набранного из таблеток оксида урана.
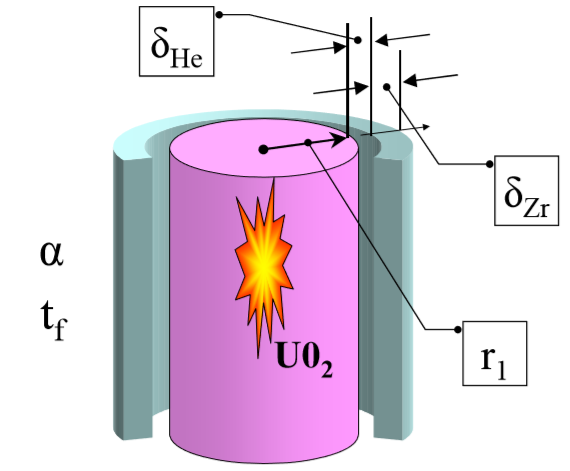
Конструкция осесимметричного ТВЭЛА (схематично)
Ядерное топливо заключено в защитную оболочку из циркониевого сплава – материала, слабо поглощающего тепловые нейтроны.
Между топливным стержнем и оболочкой имеется зазор – тонкая газовая прослойка, заполненная химически нейтральным и высокотеплопроводным гелием [2].
Мощность внутренних источников теплоты в твэлах достигает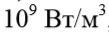 
, а теплонапряженность охлаждаемой поверхности, т.е. плотность теплового потока на поверхности оболочки –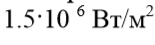 
Необходимо обеспечить эффективное охлаждение, чтобы уровень температур был приемлемым для имеющихся материалов.
В наиболее распространенных гражданских реакторах типа ВВЭР охлаждение осуществляется водой под давлением 15 MПа.
Температура насыщения при этом давлении 342ºC, а температура теплоносителя (воды) – примерно 300ºC, т.е. твэлы охлаждаются некипящей, недогретой до температуры насыщения водой. Коэффициент теплоотдачи составляет примерно 30000 Вт/(м 2 ºC).
Для оксида урана, относящегося к типу керамического ядерного топлива, температура может быть очень высокой, поскольку температура плавления UO2 составляет 2800ºC.
Однако, допустимая температура циркониевых оболочек гораздо ниже – около 400ºС. Если этот предел превышен, то в контакте с водой быстро развивается разрушительная коррозия.
При проектировании твэла необходимо проверить, не превышают ли температуры ядерного топлива и защитной оболочки допустимых значений.
Расчет проводится при заданной мощности внутренних источников qv и заданных условиях охлаждения: температуре воды tf и коэффициенте теплоотдачи α.
В конструкции твэла можно выделить две области:
• Цилиндрический стержень с внутренними источниками
• Зазор и оболочку без внутренних источников.
Модель топливного стержня – цилиндр с внутренними источниками тепла
Тепловой баланс для цилиндрического топливного стержня запишем в виде:
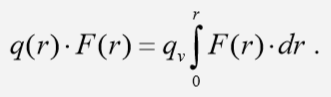
Правая часть этого выражения — есть внутреннее тепловыделение в сплошном цилиндре с текущим радиусом r, 0 ≤ r ≤ r1. Левая часть – тепловой поток через поверхность F®.
После подстановки в приведенное соотношение выражения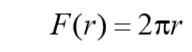 
получим уравнение:
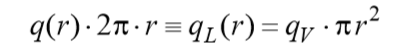. (1)
Согласно (1), линейная плотность теплового потока увеличивается по радиусу твэла благодаря действию внутренних источников теплоты.
С учетом выражения для плотности теплового потока,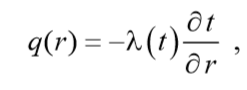
из уравнения сохранения (1) получается следующее дифференциальное уравнение для температурного поля:
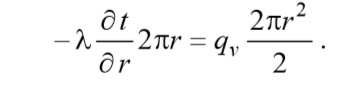(2)
Переменные в этом уравнении разделяются. Проведем интегрирование на полном интервале:
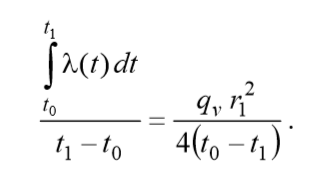
Вводя величину среднеинтегрального коэффициента теплопроводности, можно записать расчетное соотношение для перепада температуры внутри твэла в следующей компактной форме:
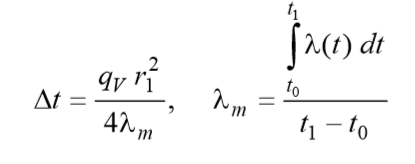(3)
Теплопроводность UO2 [3]:
(4)
# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
def Luo2(t):
return 8.706+(-9.11*(10**-3))*t+(3.992*(10**-6))*(t**2)+(-5.004*(10**-10))*(t**3)
x= np.arange(0.0,2500.0,100.0)
plt.title(' Теплопроводность оксида урана (Вт/м °С) n в зависимости от температуры (°С)')
plt.xlabel('t°С ')
plt.ylabel('$lambda(t)$ -Вт/м °C')
plt.plot(x,Luo2(x), color='b')
plt.grid(True)
plt.show()
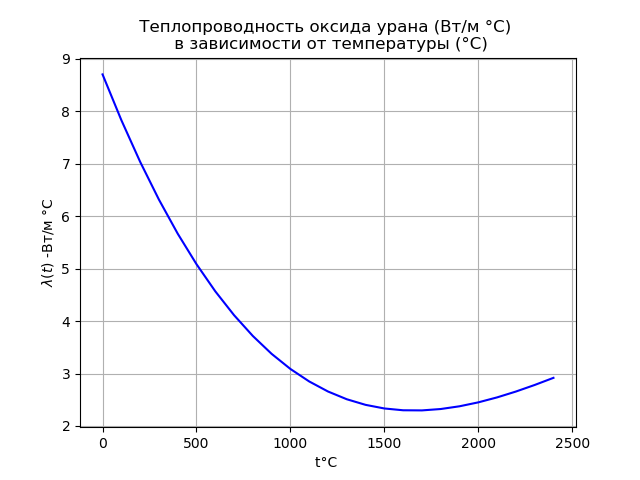
Заметим, что формула (3) дает точное решение дифференциального уравнения (2) в квадратурах. Числовые погрешности могут возникнуть при приближенном вычислении интеграла.
Если принять λ = сonst, то из (3) следует квадратичный закон изменения температуры по радиусу. Чтобы увидеть это, зафиксируйте в Δt ≡ t 0 — t1 величину t0 и рассматривайте t1 как функцию от радиуса r1.
В действительности теплопроводность оксида урана сильно зависит от температуры (4) и эту зависимость необходимо учитывать при практических расчетах.
Задаём мощность тепловыделения qv и температуру поверхности топливного стержня t1. Требуется найти температуру в центре t0 (это максимальное значение температуры в твэле).
Для таких вычислений потребовалось разработать программу на Python:
# -*- coding: utf8 -*-
import numpy as np
from scipy.optimize import *
from scipy.integrate import quad
import matplotlib.pyplot as plt
def Luo2(t):# функция теплопроводности оксида урана от температуры
return 8.706+(-9.11*(10**-3))*t+(3.992*(10**-6))*(t**2)+(-5.004*(10**-10))*(t**3)
x= np.arange(0.0,2500.0,100.0)
qv=10**9# мощность источника
r1=0.0038# радиус топливного стержня
def LLuo2(t1,t2):#функция для определения среднего интегрального значения теплопроводности оксида урана
if abs(t1-t2)<0.001:
z=Luo2(t1)
else:
z=(1/(t2-t1))*(quad(lambda t: Luo2(t), t1,t2)[0])
return z
t1=942.413# заданное значение температуры поверхности топливного стержня
t0=round(fsolve(lambda t0:t0-t1-(qv*r1**2)/(4*LLuo2(t1,t0)) ,t1)[0],1)
print(' Температура t0 в центре топливного стержня - %s °С '%t0) Получим:
Температура t0 в центре топливного стержня -2359.2 °С
Итак, чтобы воспользоваться точным решением (3) задачи о разработке математической модели твэла, потребовалось специальное использование модулей Python –fsolve и quad, а также “вложенных” функций.
Заметим, что это самый простой способ решения, если необходимо правильно учесть влияние температурной зависимости коэффициента теплопроводности ядерного топлива.
Расчет теплопередачи через зазор заполненный гелием и циркониевую защитную оболочку
Теплота, выделившаяся в активном стержне, далее передается через газовый зазор и циркониевую оболочку к охлаждающей воде.
Поскольку в этой области внутренних источников тепла нет, величина линейного потока qL сохраняется постоянной, а из (1) следует:
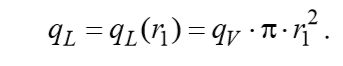
Теплопроводность гелия в газовой прослойке существенно зависит от температуры:
(5)
# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
def Lhe(t):
return 0.146+3.339*(10**-4)*t-4.219*(10**-8)*t**2
plt.title(' Теплопроводность газообразного гелия (Вт/м °С) n в зависимости от температуры (°С) ')
x= np.arange(0.0,2500.0,100.0)
plt.xlabel('t°С ')
plt.ylabel('$lambda(t)$ -Вт/м °C')
plt.plot(x,Lhe(x), color='b')
plt.grid(True)
plt.show()
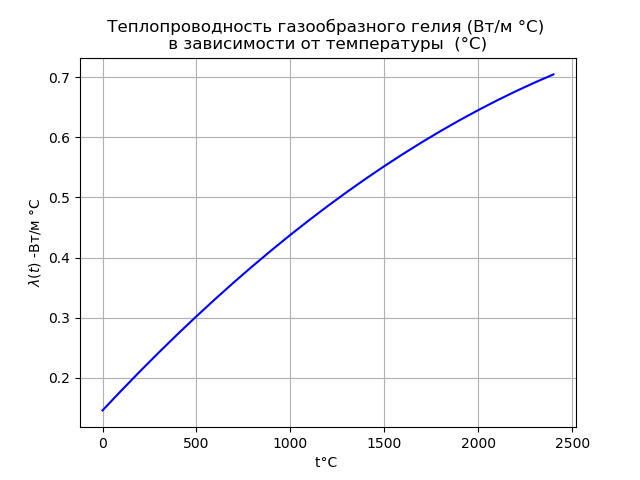
Учтем, что теплопроводность гелия в газовой прослойке существенно зависит от температуры, в то же время теплопроводность циркониевого сплава можно считать постоянной:
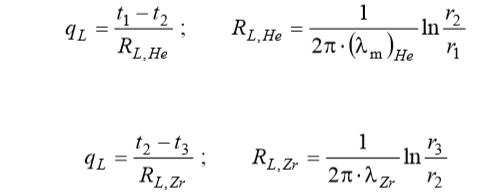
где:
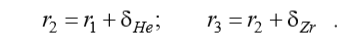
Теплоотдачу на поверхности оболочки опишем уравнением Ньютона Рихмана: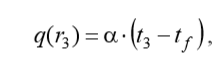
преобразованным для линейной плотности теплового потока:
,
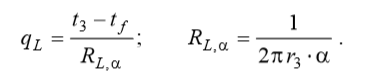где: RL,α называется линейное сопротивление теплоотдачи.
Линейные термические сопротивления гелиевого зазора, оболочки и теплоотдачи на наружной поверхности образуют последовательную цепь сопротивлений, через которые проходит одинаковый (линейный) тепловой поток qL:
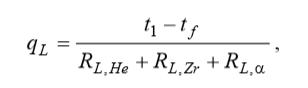(6)
Вычисления будут элементарными, если сопротивления независимы от температуры. Однако, во многих задачах теплопередачи это не так.
Сейчас мы имеем дело с самым простым примером нелинейного сопротивления, вследствие сильной температурной зависимости коэффициента теплопроводности гелия в зазоре.
Более сложными являются задачи с зависящими от температуры сопротивлениями теплоотдачи (как при кипении или конденсации, при свободной конвекции или радиационном теплообмене).
Поскольку проблема является достаточно общей, покажем, как организовать расчеты теплопередачи в таких случаях:
• Следует задать температурные зависимости материалов в виде функций, к которым могут обратиться другие блоки программы
• Следует записать термические сопротивления с учетом температурной зависимости
• Следует сформировать для последовательной цепи систему уравнений, таких как (6), содержащих неизвестные температуры t1, t2, t3.
Для таких сложных вычислений потребовалось разработать программу на Python, содержащую цепь вложенных функций:
# -*- coding: utf8 -*-
import numpy as np
from scipy.optimize import *
from scipy.integrate import quad
import matplotlib.pyplot as plt
def Luo2(t):# функция теплопроводности оксида урана от температуры
return 8.706+(-9.11*(10**-3))*t+(3.992*(10**-6))*(t**2)+(-5.004*(10**-10))*(t**3)
x= np.arange(0.0,2500.0,100.0)
qv=10**9# мощность источника
r1=0.0038# радиус топливного стержня
def LLuo2(t1,t2):#функция для определения среднего интегрального значения теплопроводности оксида урана
if abs(t1-t2)<0.001:
z=Luo2(t1)
else:
z=(1/(t2-t1))*(quad(lambda t: Luo2(t), t1,t2)[0])
return z
t1=942.413# заданное значение температуры поверхности топливного стержня
t0=round(fsolve(lambda t0:t0-t1-(qv*r1**2)/(4*LLuo2(t1,t0)) ,t1)[0],1)
print(' Температура t0 в центре топливного стержня в °С -%s'%t0)
def Lhe(t):# функция теплопроводности гелия от температуры
return 0.146+3.339*(10**-4)*t-4.219*(10**-8)*t**2
def LLhe(t1,t2):#функция для определения среднего интегрального значения теплопроводности гелия
if abs(t1-t2)<0.001:
z=Lhe(t1)
else:
z=(1/(t2-t1))*(quad(lambda t: Lhe(t), t1,t2)[0])
return z
dzr=0.00065# толщина защитной оболочки из циркония
dhe=0.0001#толщина кольцевого слоя, заполненного гелием
r2=r1+dhe#внутренний радиус защитной оболочки из циркония
r3=r2+dzr#наружный радиус защитной оболочки из циркония
Lzr=20#длина твэла
tf=300# температура охлаждающей воды
alf=30000#коэффициент теплоотдачи
RL_alf=1/(alf*2*np.pi*r3)# сопротивление теплоотдачи твэла
RL_Zr=(1/(2*np.pi*Lzr)*np.log(r3/r2))# сопротивление теплоотдачи гелия
def RL_He(t1,t2):#функция теплоотдачи гелия
return (1/(2*np.pi*LLhe(t1,t2))*np.log(r2/r1))
ql=qv*np.pi*r1**2#величина линейного теплового потока от стержня из оксида урана
def fun(t1,t2,t3): #функция для определения температур на поверхности стержня из диоксида урана
z=(t1-tf-ql*(RL_He(t1,t2)+RL_Zr+RL_alf))
return z
t3=tf+ql*RL_alf
t2=t3+ql*RL_Zr
tt0=400#начальное значение для поиска t1
t1=fsolve(lambda t1:fun(t1,t2,t3),tt0)[0]# определение t1
print('Температура t1 поверхности топливного стержня из оксида урана-%s °С'%round(t1,1))
print('Температура t2 внутренней поверхности оболочки из циркония -%s °С'%round(t2,1))
print('Температура t3 наружной поверхности оболочки из циркония -%s °С'%round(t3,1))Получим:
Температура t0 в центре топливного стержня — 2359.2 °С
Температура t1 поверхности топливного стержня из оксида урана-942.4 °С
Температура t2 внутренней поверхности оболочки из циркония -408.5 °С
Температура t3 наружной поверхности оболочки из циркония -352.9 °С
Распределение температуры в твэле
# -*- coding: utf8 -*-
import numpy as np
from scipy.optimize import *
from scipy.integrate import quad
import matplotlib.pyplot as plt
def Luo2(t):# функция теплопроводности оксида урана от температуры
return 8.706+(-9.11*(10**-3))*t+(3.992*(10**-6))*(t**2)+(-5.004*(10**-10))*(t**3)
x= np.arange(0.0,2500.0,100.0)
qv=10**9# мощность источника
r1=0.0038# радиус топливного стержня
def LLuo2(t1,t2):#функция для определения среднего интегрального значения теплопроводности оксида урана
if abs(t1-t2)<0.001:
z=Luo2(t1)
else:
z=(1/(t2-t1))*(quad(lambda t: Luo2(t), t1,t2)[0])
return z
t1=942.413# заданное значение температуры поверхности топливного стержня
t0=round(fsolve(lambda t0:t0-t1-(qv*r1**2)/(4*LLuo2(t1,t0)) ,t1)[0],1)
print(' Температура t0 в центре топливного стержня - %s °С'%t0)
def Lhe(t):# функция теплопроводности гелия от температуры
return 0.146+3.339*(10**-4)*t-4.219*(10**-8)*t**2
def LLhe(t1,t2):#функция для определения среднего интегрального значения теплопроводности гелия
if abs(t1-t2)<0.001:
z=Lhe(t1)
else:
z=(1/(t2-t1))*(quad(lambda t: Lhe(t), t1,t2)[0])
return z
dzr=0.00065# толщина защитной оболочки из циркония
dhe=0.0001#толщина кольцевого слоя, заполненного гелием
r2=r1+dhe#внутренний радиус защитной оболочки из циркония
r3=r2+dzr#наружный радиус защитной оболочки из циркония
Lzr=20#длина твэла
tf=300# температура охлаждающей воды
alf=30000#коэффициент теплоотдачи
RL_alf=1/(alf*2*np.pi*r3)# сопротивление теплоотдачи твэла
RL_Zr=(1/(2*np.pi*Lzr)*np.log(r3/r2))# сопротивление теплоотдачи гелия
def RL_He(t1,t2):#функция теплоотдачи гелия
return (1/(2*np.pi*LLhe(t1,t2))*np.log(r2/r1))
ql=qv*np.pi*r1**2#величина линейного теплового потока от стержня из оксида урана
def fun(t1,t2,t3): #функция для определения температур на поверхности стержня из диоксида урана
z=(t1-tf-ql*(RL_He(t1,t2)+RL_Zr+RL_alf))
return z
t3=tf+ql*RL_alf
t2=t3+ql*RL_Zr
tt0=400#начальное значение для поиска t1
t1=fsolve(lambda t1:fun(t1,t2,t3),tt0)[0]# определение t1
print('Температура t1 поверхности топливного стержня из оксида урана-%s °С'%round(t1,1))
print('Температура t2 внутренней поверхности оболочки из циркония -%s °С'%round(t2,1))
print('Температура t3 наружной поверхности оболочки из циркония -%s °С'%round(t3,1))
def eq(t,r):# вспомогательная функция для определения распределения температуры вдоль радиуса топливного стержня
return t0-t-qv*r**2/(4*LLuo2(t,t0))
def t_tuel(r):#функция для определения распределения температуры вдоль радиуса топливного стержня
return fsolve(lambda t:eq(t,r) ,t0)[0]
def t_out(r):#функция для определения распределения температуры от радиуса топливного стержня за наружную оболочку
if r2<r<=r3:
z=t2+(t3-t2)*np.log(r/r2)/np.log(r3/r2)
elif r1<=r<=r2:
z=t1+(t2-t1)*np.log(r/r1)/np.log(r2/r1)
elif r>r3:
z=tf
return z
tt1=[t_tuel(r) for r in np.arange(0.0,r1+0.0001,0.0001)]
rr1=np.arange(0.0,r1+0.0001,0.0001)
tt2=[t_out(r) for r in np.arange(r1,r3+0.001,0.0001)]
rr2=np.arange(r1,r3+0.001,0.0001)
plt.title('Температурное поле в твэле ядерного реактора')
plt.plot(rr1,tt1, color='r',linewidth=2, label=' 0<=r<=r1')
plt.plot(rr2,tt2, color='b',linewidth=2, label='r1<r<=r3+0.001 ')
plt.plot(0,t0,'o',label='t0=%s°С '%t0)
plt.plot(r1, t_tuel(r1),'o',label='t1=%s °С'%round(t_tuel(r1),1))
plt.plot(r2, t_out(r2),'o',label='t2=%s °С'%round(t_out(r2),1))
plt.plot(r3, t_out(r3),'o',label='t3=%s °С'%round(t_out(r3),1))
plt.plot(r3+0.001, t_out(r3+0.001),'o',label='tf=%s °С'%round(t_out(r3+0.001),1))
plt.xlabel("r в м.")
plt.ylabel("t в °С")
plt.grid(True)
plt.legend(loc='best')
plt.show()
Получим:
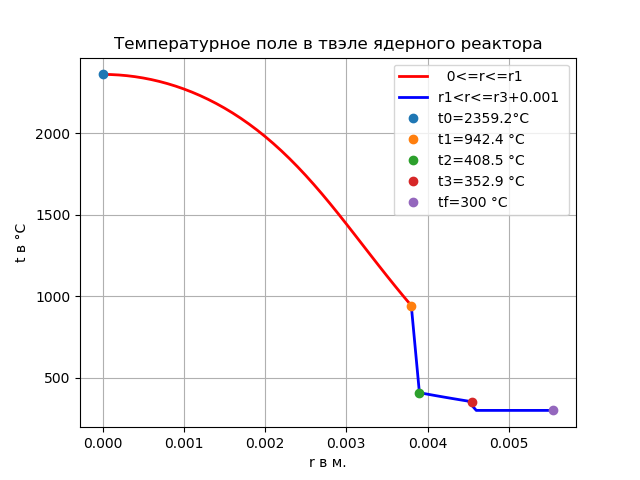
Результаты расчета твэла представлены на графике как распределение температуры по радиусу. Основное внимание при оценке результатов должно быть уделено двум значениям:
1. максимальной температуре ядерного топлива t0. Максимальное предельное значение можно оценить, как температуру плавления оксида урана, примерно 2800°С,
2. температуре поверхности защитной оболочки t3, где происходит контакт с водой. Допустимая температура оболочек из циркониевых сплавов – около 400ºС. При более высокой температуре в контакте с водой быстро развивается разрушительная коррозия.
Таким образом, рассмотренный температурный режим близок к предельному по теплонапряженности.
Выводы:
Средствами свободно распространяемого языка программирования Python с использованием модулей quad, fsole и системы вложенных функций разработана математическая модель для осесимметричного твэла ядерного реактора.
Ссылки:
1. Тепловыделяющий_элемент.
2. Тепломассообмен в энергетических установках.
3. Свойства оксида урана, КТР закиси-окиси.
Автор: Юрий Тараненко
