Это заключительная часть статей о сверточных сетях. Перед прочтением рекомендую ознакомиться с первой и второй частями, в которых рассматриваются слои сети и принципы их работы, а также формулы, которые отвечают за обучение всей модели. Сегодня мы рассмотрим особенности и трудности, с которыми можно столкнуться при тестировании вручную написанной на python сверточной сети, применим написанную сеть к датасету MNIST и сравним полученные результаты с библиотекой tensorflow.
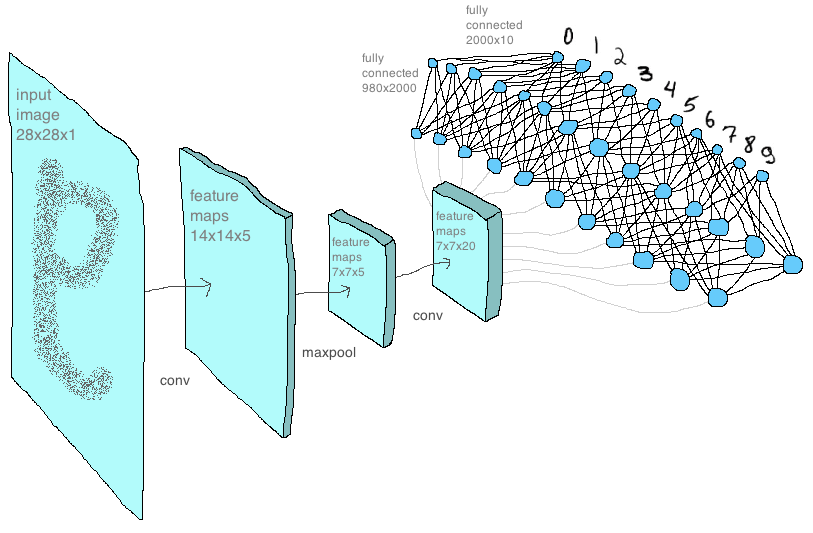
Сейчас уже можно видеть основную концепцию сети, структуру слоев и их последовательности. Ниже я представил ее таким образом, каким реализовал в коде — каждый слой в виде отдельной функции (вы в качестве эксперимента можете убрать или добавить новые слои, поменять их местами или написать свой новый слой):
Прямое прохождение через сеть
1) Первый слой сверточной сети
2) Слой макспулинга
3) Второй слой сверточной сети
4) Сложение всех карт признаков в один вектор (это не совсем “полноценный” слой, но все-таки занимает здесь важное место)
5) Первый слой fc-сети
6) Второй слой fc-сети
7) Вычисление значение loss-функции
Обратное прохождение через сеть и обновление параметров (проходим через все слои в обратном порядке)
8) Backprop через loss
9) Второй слой fc-сети
10) Первый слой fc-сети
11) Разворачивание карт признаков из вектора (также не является “полноценным” слоем)
12) Второй слой сверточной сети
13) Слой макспулинга
14) Первый слой сверточной сети
Конечно, не стоит ожидать, чтобы эта модель работала быстрее, чем оптимизированная библиотека для машинного обучения. Но ведь конечная цель — не написать быструю реализацию, а понять, как работает библиотека, научиться самостоятельно строить нейросеть на самом низком уровне, а после предыдущих статей с рассмотренными принципами работы и формулами остается только написать код. Далее пример такого кода.
model.py — здесь хранятся все основные функции, из которых составлена сеть. Многие из функций мы уже рассмотрели в прошлых статьях.
np_mnist_train_test.py — сама сеть и входные параметры для нее. Сеть строится из функций, определенных в model.py, и выглядит буквально таким же образом, как 14 пунктов, которые мы определили в начале статьи:
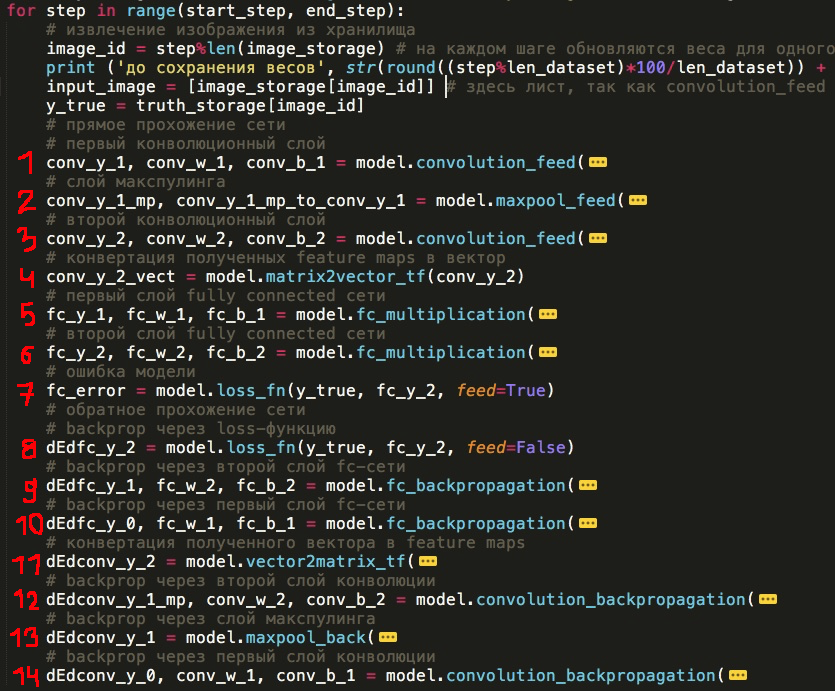
(Аргументы функций я скрыл, в развернутом виде все выглядит жутковато)
Но перед тем, как перейти к описанию результатов, хотелось бы остановиться на другом. Применяя написанную модель к данным, я видел, что она обучалась и все проходило без ошибок. Однако хотелось быть уверенным, что сеть работает правильно, что все внутренние расчеты корректны. И самым очевидным решением было — сравнить эту модель с аналогичной архитектурой на tensorflow, используя, например, MNIST в качестве датасета.

На tensorflow написать сеть было значительно легче, фактически же я просто взял вот этот вариант из руководства tensorflow и немного подправил параметры. Получилось такая модель:
Чтобы убедиться, что результаты обеих моделей совпадают, нужно изначально убедиться, что их стартовые веса идентичны. Тут состояла первая трудность — у меня не получилось закрепить сиды отдельно для numpy и tensorflow таким образом, чтобы начальные генерируемые случайным образом матрицы весов совпадали. Я придумал такую хитрость: создать веса в tesnrflow и подать их в обе модели. Но, мне кажется, что этот вопрос можно было решить и как-то проще. Но, в итоге, все выглядит таким образом:
import numpy as np
import tensorflow as tf
tf_w = tf.truncated_normal([2, 2, 1, 4], stddev=0.1)
with tf.Session() as sess:
np_w = sess.run(tf_w)
print('n Так выглядят веса tensorflow: n n', np_w)
print('n n Простая итерация по тензору не дает нужного результата:')
for i in range(len(np_w)):
print('n', np_w[i])
conv_w = []
np_w = np.reshape(np_w, (np_w.size,))
np_w = np.reshape(np_w, (4,2,2), order='F')
print('n n А вот матрицы в том виде, как их извлекат tensorflow:')
for i in range(4):
conv_w.append(np_w[i].T)
print('n', conv_w[-1])
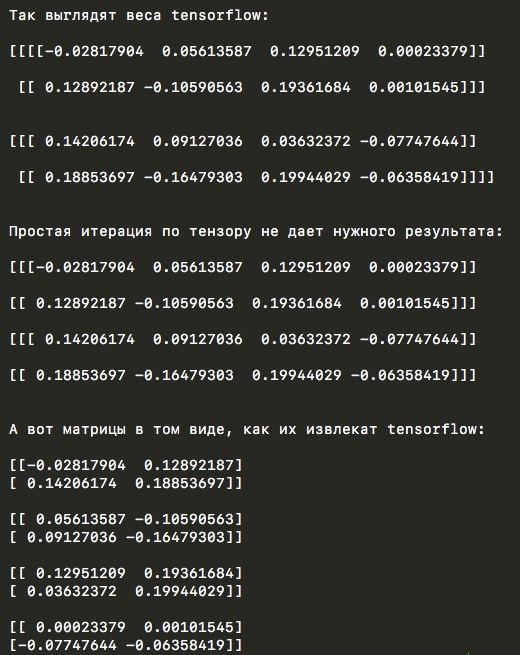
Чтобы извлечь веса из тензора в том порядке, каким их видит tensorflow, то есть таким образом, каким они используются в дальнейшей работе внутри библиотеки, я и использовал код выше. Как видите, все не совсем тривиально: tensorflow-тензору пришлось пройти пару решейпов и транспонирование, чтобы его можно было использовать в numpy-модели. Также по этой причине пришлось переписать и некоторые другие функции. Например, функция по объединению всех feature maps в один вектор — когда после слоев конволюции образуется много feature maps и необходимо их векторизовать для подачи в fc-сеть. После того, как мы разбили тензор на матрицы по вышеописанному способу, объединить матрицы просто так в вектор уже нельзя, если мы хотим, чтобы это выглядело так же, как внутри tensorflow. И для того, чтобы добиться этого, мы должны сделать следующее:
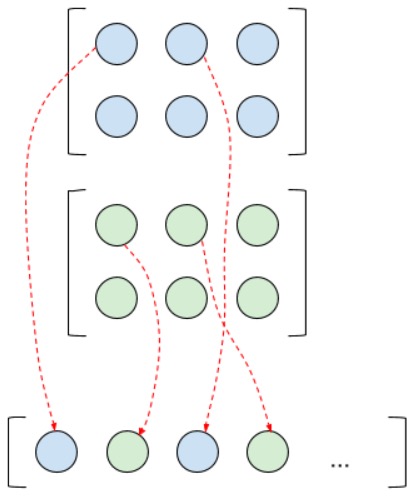
Соответственно, когда при обратном распространении ошибки мы прошли полносвязные слои, у нас будет вектор градиентов, который нужно “расправить” обратно в карты признаков. Делается это как на картинке выше, только в обратную сторону. Конечно, если перед нами не стоит цели сравнить результаты вычислений numpy- и tenosorflow-моделей, эти функции можно написать простым способом. Вот, фактически, я и описал, что делают функции matrix2vector (преобразование матриц в вектор) и vector2matrix (вектора в матрицу) в model.py.
Следующее: карты признаков рассматриваются как каналы одного, так сказать, изображения, а не как независимые друг от друга изображения. Изначально я предполагал, что, если мы хотим на выходе четыре feature maps, то и ядра должно быть четыре, но выходит все немного по-другому. Так как все карты признаков предыдущего слоя рассматриваются как одно изображение со множеством каналов, то для получения только одной карты на следующем слое нужно создать столько матриц весов, сколько каналов на предыдущем слое (соответсвтенно, для двух карт — вдвое больше матриц весов). Затем получить соответствующее число “промежуточных” карт и сложить их в одну — это и будет искомый один feature map. Вот, скажем, если на предыдущем слое получилось две карты, и мы на следующем слое хотим получить четыре, то выглядеть это будет примерно так:
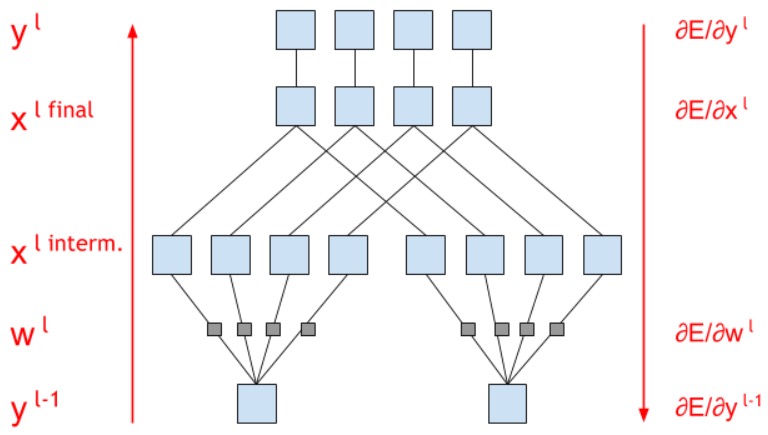
При сложении “промежуточные” карты признаков как будто перемешиваются для получения “финальной” карты, но, если присмотреться, то понятно, что на самом деле суммируются в итоговые карты только те “промежуточные” карты признаков, которые происходят из разных каналов исходного слоя. Может быть, благодаря изображению ниже будет понятно лучше:
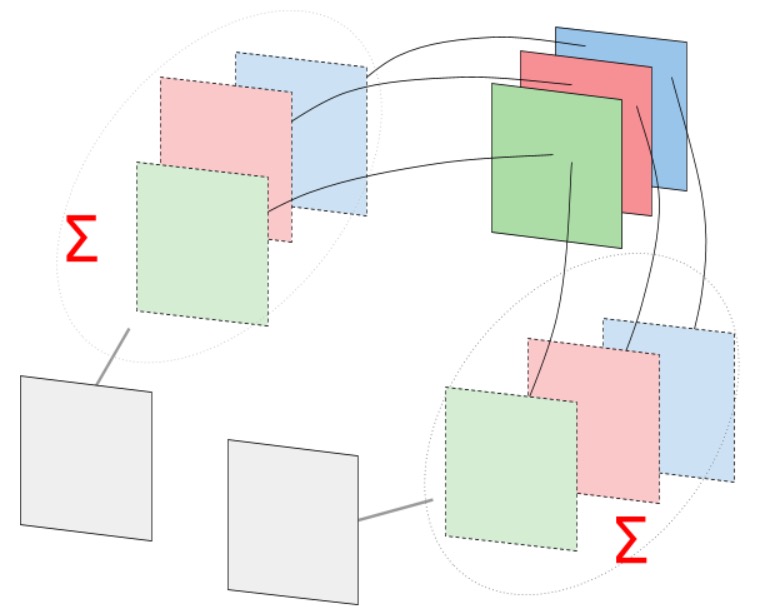
Здесь мы из одной RGB картинки хотим получить две feature maps. И еще отмечу: при обратном распространении ошибки те “промежуточные” карты вообще никак не задействуются: в понимании программы их вообще не существует. Каждая матрица весов и карта признаков из предыдущего слоя завязаны на соответствующие им “финальные” карты следующего слоя.
Следующей особенностью вычислений tensorflow было то, что внутри функции tf.nn.conv2d происходит на самом деле кросс-корреляция и об это даже написано в руководстве tensorflow:
Note that although these ops are called «convolution», they are strictly speaking «cross-correlation» since the filter is combined with an input window without reversing the filter. For details, see the properties of cross-correlation.
Но это не стало большой проблемой, так как в моей реализации на numpy достаточно поменять True на False. Вот пример кода, с помощью которого можно убедиться, что используется именно кросс-корреляция:
import tensorflow as tf
import numpy as np
np.random.seed(0)
tf.set_random_seed(0)
# from pudb import set_trace; set_trace() # для дебага
# для закрепления случайных значений и сравнения с numpy
tf_w1 = tf.truncated_normal([3, 3, 1, 1], stddev=0.1)
with tf.Session() as sess:
w1 = sess.run(tf_w1)
x = tf.constant(0.1, shape=[4, 4])
input_image = tf.reshape(x, [-1, 4, 4, 1])
w_conv1 = tf.Variable(w1)
h_conv1 = tf.nn.conv2d(input_image, w_conv1, strides=[1, 1, 1, 1], padding='SAME')
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
w_conv = sess.run(h_conv1)
w_conv = np.reshape(w_conv, (w_conv.size,))
w_conv = np.reshape(w_conv, (1,4,4), order='F') # здесь необходимо руками поставить размерность выходного тезнора!
print('n результат операции "конволюции" в tensorflow:')
for i in range(1):
print(w_conv[i].T)
w1 = np.reshape(w1, (w1.size,))
w1 = np.reshape(w1, (1,3,3), order='F')
for i in range(1):
w_l = w1[i].T
y_l_minus_1 = np.array([
[0.1,0.1,0.1,0.1],
[0.1,0.1,0.1,0.1],
[0.1,0.1,0.1,0.1],
[0.1,0.1,0.1,0.1]])
other_parameters={
'convolution':False,
'stride':1,
'center_w_l':(1,1),
}
def convolution_feed_x_l(y_l_minus_1, w_l, conv_params):
indexes_a, indexes_b = create_indexes(size_axis=w_l.shape, center_w_l=conv_params['center_w_l'])
stride = conv_params['stride']
# матрица выхода будет расширяться по мере добавления новых элементов
x_l = np.zeros((1,1))
# в зависимости от типа операции меняется основная формула функции
if conv_params['convolution']:
g = 1 # операция конволюции
else:
g = -1 # операция корреляции
# итерация по i и j входной матрицы y_l_minus_1 из предположения, что размерность выходной матрицы x_l будет такой же
for i in range(y_l_minus_1.shape[0]):
for j in range(y_l_minus_1.shape[1]):
demo = np.zeros([y_l_minus_1.shape[0], y_l_minus_1.shape[1]]) # матрица для демонстрации конволюции
result = 0
element_exists = False
for a in indexes_a:
for b in indexes_b:
# проверка, чтобы значения индексов не выходили за границы
if i*stride - g*a >= 0 and j*stride - g*b >= 0
and i*stride - g*a < y_l_minus_1.shape[0] and j*stride - g*b < y_l_minus_1.shape[1]:
result += y_l_minus_1[i*stride - g*a][j*stride - g*b] * w_l[indexes_a.index(a)][indexes_b.index(b)] # перевод индексов в "нормальные" для извлечения элементов из матрицы w_l
demo[i*stride - g*a][j*stride - g*b] = w_l[indexes_a.index(a)][indexes_b.index(b)]
element_exists = True
# запись полученных результатов только в том случае, если для данных i и j были произведены вычисления
if element_exists:
if i >= x_l.shape[0]:
# добавление строки, если не существует
x_l = np.vstack((x_l, np.zeros(x_l.shape[1])))
if j >= x_l.shape[1]:
# добавление столбца, если не существует
x_l = np.hstack((x_l, np.zeros((x_l.shape[0],1))))
x_l[i][j] = result
# вывод матрицы demo для отслеживания хода свертки
# print('i=' + str(i) + '; j=' + str(j) + 'n', demo)
return x_l
def create_axis_indexes(size_axis, center_w_l):
coordinates = []
for i in range(-center_w_l, size_axis-center_w_l):
coordinates.append(i)
return coordinates
def create_indexes(size_axis, center_w_l):
# расчет координат на осях ядра свертки в зависимости от номера центрального элемента ядра
coordinates_a = create_axis_indexes(size_axis=size_axis[0], center_w_l=center_w_l[0])
coordinates_b = create_axis_indexes(size_axis=size_axis[1], center_w_l=center_w_l[1])
return coordinates_a, coordinates_b
print('n результат операции кросс-корреляции:')
print(convolution_feed_x_l(y_l_minus_1, w_l, other_parameters))
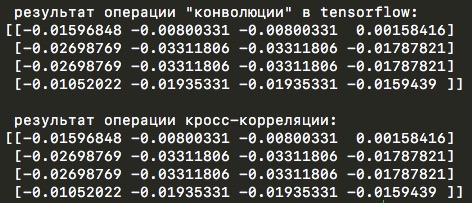
Этот же демонстрационный код содержит в себе еще одну интересную деталь расчетов в tensorflow. Внутри библиотеки во время операции конволюции иногда меняется центральный элемент ядра свертки. Обычно он находится в позиции (0,0), но для ядра 3 на 3 перемещается в центральную позицию (1,1) (а может, на самом деле, все наоборот и “обычная” позиции как раз в центре (1,1) и относительно нее ядро и перемещается в левый верхний угол...). Если же для этого ядра мы установим шаг (stride) равным двум, то центральный элемент в tensorflow снова переместится в нулевую позицию. Логика в том, как мне кажется, что при размерности входной матрицы 4 на 4 пикселя и шаге в два пикселя, мы ожидаем выходную матрицу размерности 2 на 2. И ровно так и происходит, но только если центральный элемент расположен в позиции (0,0), если же центральный элемент находится в (1,1), то размерность выходной матрицы при таких условиях будет равной три на три пикселя. Происходит это из-за того, что ядро с центральным элементом в (1,1) успевает произвести больше вычислений перед тем, как “скроется” за пределами входной матрицы. Вот, посмотрите на картинке ниже:
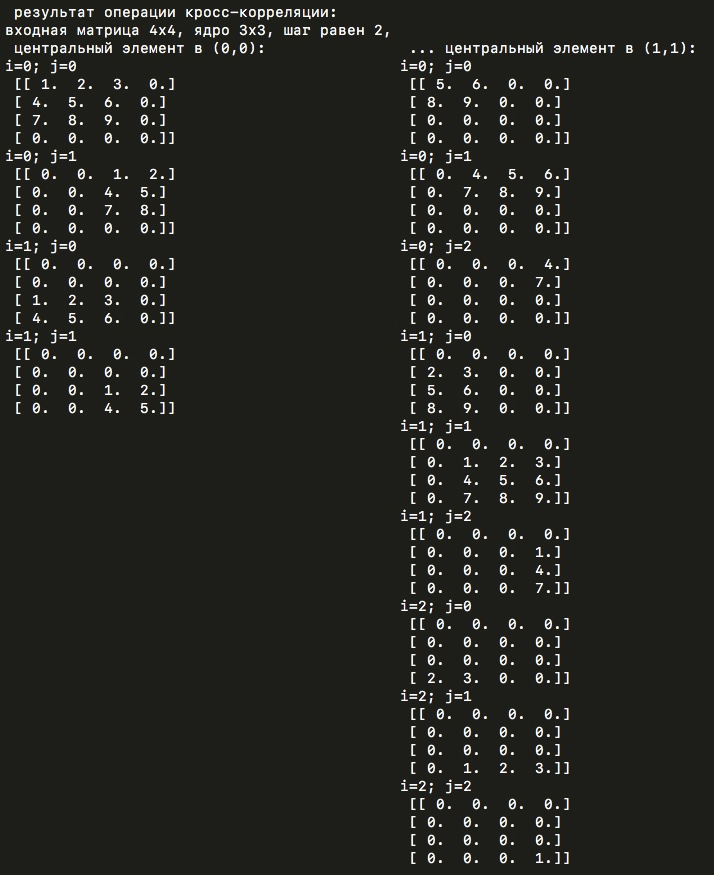
И, таким образом, если в коде, написанном с нуля, не учесть возможность выбора центрального элемента, то можно было бы никогда и не понять причину отличий результатов от tensorflow.
Итак, наконец мы разобрали все те нюансы, что приводили к отличиям результатов, учли все это в модели from scratch и можем сравнить лоссы обеих сетей: первой, реализованной с помощью numpy, и второй — библиотеки на tensorflow.
Далее немного об архитектуре сетей. На первом сверточном слое я использовал ядро 2х2 пикселя (и центральный элемент в нулевой позиции) с шагом равным двум, этот слой производит пять карт признаков размерности 14х14 пикселей (то есть в два раза меньше исходных mnist-изображений 28х28 пикселей). Эти карты подаются на второй слой с ядром уже три на три пикселя и шагом один (что, напомню, приводит к смещению центрального элемента, собственно, в центр ядра), и на выходе 20 карт признаков такой же размерности. Далее слой макспулинга, снижающий размерность карт до 7х7 пикселей. Затем карты складываются в вектор. Следующим идет скрытый слой полносвязной сети с двумя тысячами нейронов. На этом слое в матрице весов получается почти два миллиона (7 х 7 х 20 х 2000 = 1 960 000) элементов! И далее уже 2000 нейронов соединены с 10 выходными нейронами, отвечающими за количество классов: то есть 10 цифр, которые сеть должна научиться предсказывать. Все эти параметры перечислены в словаре под названием model settings, который находится внутри файла np_mnist_train_test.py:
Итак, попробуем запустить обе модели и сравнить результаты: loss и accuracy, усредненных по каждым пяти изображениям:
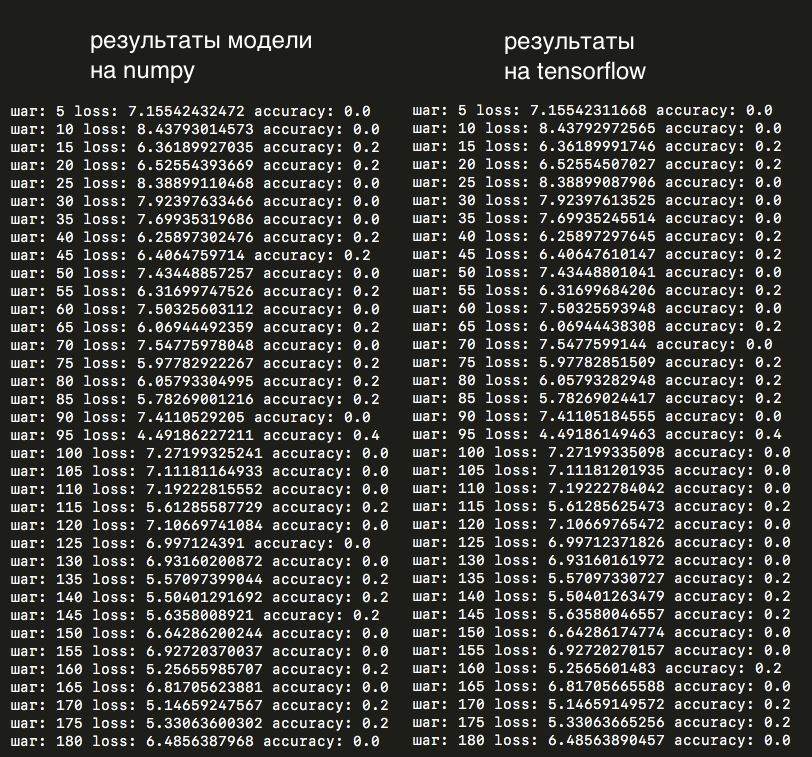
Как видно, лоссы в практически полностью совпадают, а значит все вычисления внутри собранной вручную модели и модели, написанной на tensorflow, как минимум очень схожи.
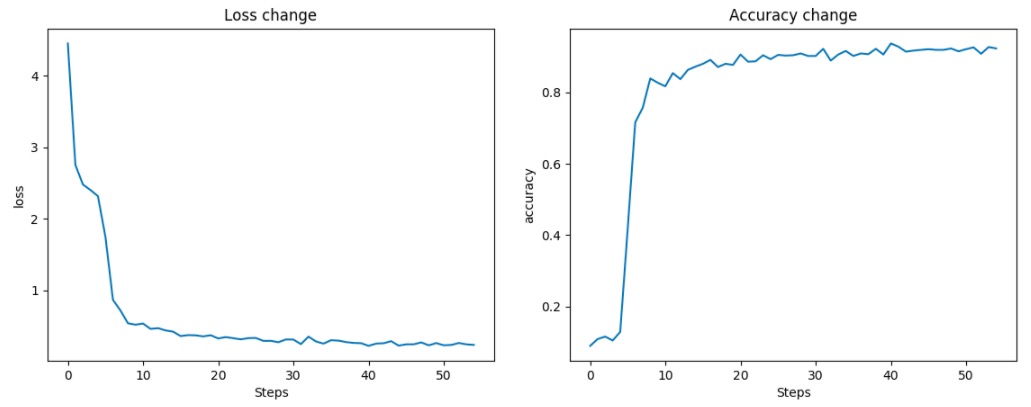
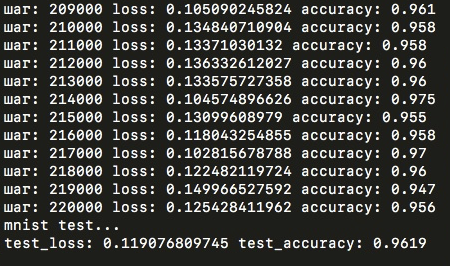
По прошествии дня и одной эпохи обучения (то есть 55 тысяч итераций прямого и обратного прохождения сети), получились такие графики для loss и accuracy:
И на тестовой выборке accuracy составляет 89%:
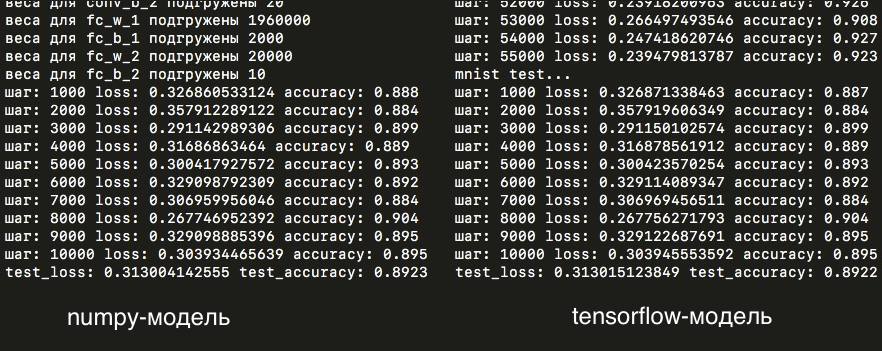
Как можно видеть, loss для сборной numpy-модели на тестовой и обучающей выборках очень похожи на результаты сети на tensorflow. Отличие же в accuracy на тестовой выборке по прошествии одной эпохи обучения составляет всего одно изображение на десять тысяч! Но все же сами матрицы весов отличаются в тысячных знаках (тогда как на первых этапах обучения не было никакой разницы) — различие, скорее всего, обусловлено разной точностью расчетов в numpy и tensorflow: float32 и float64, либо другими неучтенным нюансами, которые вносят незначительные отличия в расчетах моделей.
Accuracy 89% было достигнуто всего после прохождения одной эпохи. Но после уже четырех эпох на этой же модели результаты на тестовой выборке были бы значительно выше — 96%. Но попробовал я это только на tensorflow, на numpy-модели дальнейшее обучение заняло было слишком много времени, но в целом можно заключить, что подобранная архитектура не так плоха, как могла бы быть!
Если быть точным, одна эпоха на numpy-модели заняла на стареньком ноутбуке примерно 15 часов. На модели, собранной с помощью tensorflow, эта же эпоха проходит всего за 7-8 минут. То есть разница в 120 раз! На что же уходит все время в собранной вручную модели и где узкое место? Чтобы понять это, достаточно взглянуть на график времени, которое занимает каждая функция в numpy-модели (суммарно для прямого и обратного прохождений по сети):
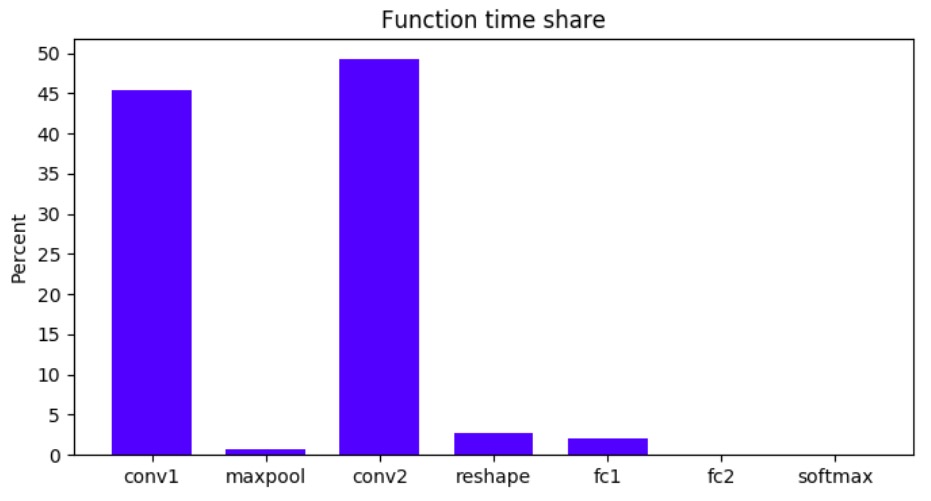
Как видно, почти все 15 часов обучаются несколько ядер свертки. Именно поэтому в параметрах модели у меня так мало карт признаков на выходе сверточных слоев. На полносвязные слои почти не уходит времени (особенно на второй fc-слой с меньшим количеством параметром), так как внутри происходит оптимизированное перемножение numpy-матриц, тогда как сверточные функции писались исходя из формул и буквального “движения” ядра по матрице. Вычисления tensorflow гораздо оптимизированнее и конволюционные слои также представлены в виде перемножения матриц. Здесь можно прочесть подробнее.
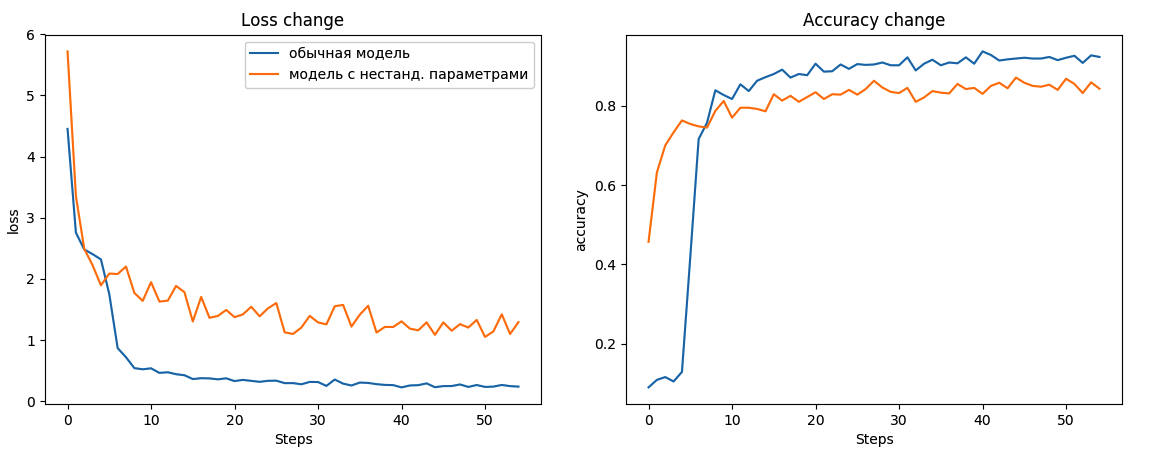
Попробовал обучение модели с “нестандартными” параметрами — операцией конволюции вместо кросс-корреляции и центральными элементами в позиции (1,0) для первого слоя и (1,2) для второго слоя свертки. Результаты получились хуже, однако при дальнейшем обучении, возможно, и выровнялись бы с обычными параметрами. Сравнить вычисления с tensorflow-моделью, конечно, здесь уже не мог, так как не представляется возможным поменять в tensorflow заданный центральный элемент на любой другой или кросс-корреляцию на конволюцию для какого бы то ни было слоя сверточной сети (в целом, вряд ли это может пригодится когда-нибудь). Интересно, что accuracy в самом начале резко начала расти вверх, но после уже сильно отставала от “обычной” модели.
Конечно, numpy-модель не годится для настоящих расчетов и использовать следует tensorflow или другие библиотеки для машинного обучения. Я не могу сказать, что совершенно уверен в отсутствии ошибок в реализации на python, что учтены все тонкости и нюансы обучения, которые абсолютно точно есть в tensorflow. Но главное — это время обучения. То, что на python занимает два часа, на tensorflow — всего минуту.
Для улучшения же полученных на MNIST результатов нужно использовать больше конволюционных слоев, генерировать больше feature maps для адекватного извлечения сетью признаков из изображений (все это, конечно, серьезно отразится на времени обучения, если использовать модель на numpy). Также следует использовать батч больше, чем в одно изображение, классический метод оптимизации SGD заменить на, например, Adam (о которых можно почитать здесь или здесь). Полученные нами в статье результаты, конечно, не впечатляющие (лидерборд можно увидеть здесь), зато видно, что модель, написанная буквально согласно формулам, действительно учится, работает. Если вы хотите воспроизвести тестовые результаты, либо продолжить обучение, в репозитории на гите лежат веса cnn_weights_mnist.npy для numpy-модели.
Вот и подошли к завершению статьи о сверточных сетях. Хорошо, если сейчас вы уже имеете представление о внутреннем устройстве и математике, которая стоит за сетями и скрыто внутри библиотеки для машинного обучения. Я попытался все рассказывать максимально простым языком и разобрать все формулы так, чтобы не осталось никаких вопросов, и надеюсь что эти статьи сэкономили кому-нибудь время. Что ж, на этом все, спасибо, что прочли до конца!
Автор: Калинин Станислав





