Введение
На финансовом рынке обращается, как правило, несколько типов ценных бумаг: государственные ценные бумаги, муниципальные облигации, корпоративные акции и т.п.
Если у участника рынка есть свободные деньги, то их можно отнести в банк и получать проценты или купить на них ценные бумаги и получать дополнительный доход. Но в какой банк отнести? Какие ценные бумаги купить?
Ценные бумаги с низкими рисками, как правило, малодоходны, а высокодоходные, как правило, более рискованны. Экономическая наука может дать некоторые рекомендации для решения этого вопроса, но для этого необходимо иметь соответствующие программные средства, желательно с простым интерфейсом и бесплатные.
Программные средства для анализа портфелей ценных бумах должны работать с матрицами доходности и решать задачи нелинейного программирования с ограничениями в виде строгих и нестрогих неравенств. Символьное решение на Python некоторых типов задач нелинейного программирования мною уже рассматривалось в публикации [1]. Однако, применить предложенные в указанной публикации методы для анализа портфеля ценных бумаг нельзя из-за ограничений в виде строгих неравенств.
Целью настоящей публикации является разработка методов оптимизации портфелей ценных бумаг с использованием библиотеки scipy.optimize. Пришлось исследовать и применить при программировании такие мало известные возможности указанной библиотеки, как введение дополнительных ограничений в функцию цели [2].
Постановка задачи об оптимальном портфеле Марковица
Рассмотрим общую задачу распределения капитала, который участник рынка хочет потратить на приобретение ценных бумаг. Цель инвестора – вложить деньги так, чтобы сохранить свой капитал, а при возможности и нарастить его.
Набор ценных бумаг, находящихся у участника рынка, называется его портфелем. Стоимость портфеля – это суммарная стоимость всех составляющих его бумаг. Если сегодня его стоимость есть Р, а через год она окажется равной Р', то (Р'- Р)/Р естественно назвать доходностью портфеля в процентах годовых. Доходность портфеля – это доходность на единицу его стоимости.
Пусть xi – доля капитала, потраченная на покупку ценных бумаг i-го вида. Весь выделенный капитал принимается за единицу. Пусть di – доходность в процентах годовых бумаг i-го вида в расчете на одну денежную единицу.
Доходность колеблется во времени, так что будем считать ее случайной величиной. Пусть mi, ri – средняя ожидаемая доходность и среднее квадратическое отклонение, называемое риском. Через CVij обозначим ковариацию доходностей ценных бумаг i – го и j – го видов.
Каждый владелец портфеля ценных бумаг сталкивается с дилеммой: хочется иметь эффективность больше, а риск меньше. Однако, поскольку “нельзя поймать двух зайцев сразу”, необходимо сделать определенный выбор между эффективностью и риском.
Модель оптимального портфеля Марковица, которая обеспечивает минимальный риск и заданную доходность
Такая модель в виде системы из уравнений и неравенств имеет вид [3]:
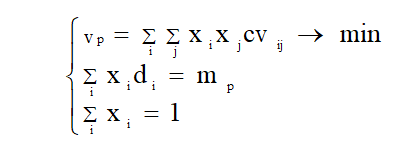
Необходимо определить: x1,x2…xn.
Исходными данными для расчета является матрица доходности ценных бумаг следующей формы (заполненный пример матрицы в листинге программы):
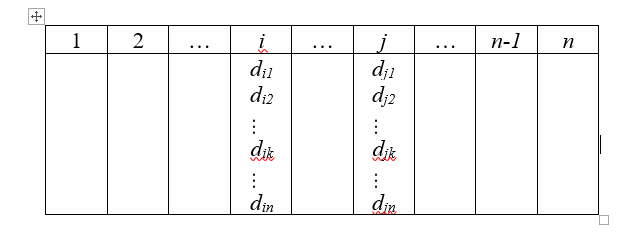
Для реализации модели минимального риска на Python нужно выполнить следующие этапы разработки:
1.Определение средней доходности акций 1-6:
from sympy import *
import numpy as np
from scipy.optimize import minimize
from sympy import *
import numpy as np
from scipy.optimize import minimize
"D- матрица доходности (обычно загружается из файла)"
D=np.array([[9.889, 11.603,11.612, 12.721,11.453,12.102],
[12.517, 13.25,12.947,12.596,12.853,13.036],
[12.786, 12.822,15.447,14.452,15.143,16.247],
[11.863, 12.114,13.359,13.437,11.913,15.300],
[11.444, 13.292,13.703,11.504,13.406,15.255],
[14.696, 15.946,16.829,17.698,16.051,17.140]],np.float64)
d= np.zeros([6,1])# столбец для средней доходности
m,n= D.shape#размерность матрицы
for j in np.arange(0,n):
for i in np.arange(0,m):
d[j,0]=d[j,0]+D[i,j]
d=d/n
print("Средняя доходность акций 1-6 : n %s"%d)Получим:
Средняя доходность акций 1-6:
[[ 12.19916667]
[ 13.17116667]
[ 13.98283333]
[ 13.73466667]
[ 13.46983333]
[ 14.84666667]]
2. Построение ковариационной матрицы (m=n=6).
CV= np.zeros([m,n])
for i in np.arange(0,m):
for j in np.arange(0,n):
x=np.array(D[0:m,j]).T
y=np.array(D[0:m,i]).T
X = np.vstack((x,y))
CV[i,j]=round(np.cov(x,y,ddof=0)[1,0],3)
print(«Ковариационная матрица CV: n %s»%CV)
Получим:
Ковариационная матрица CV:
[[ 2.117 1.773 2.256 2.347 2.077 1.975]
[ 1.773 1.903 1.941 2.049 1.888 1.601]
[ 2.256 1.941 2.901 2.787 2.701 2.761]
[ 2.347 2.049 2.787 3.935 2.464 2.315]
[ 2.077 1.888 2.701 2.464 2.723 2.364]
[ 1.975 1.601 2.761 2.315 2.364 3.067]]
3. Символьное определение функции для определения дисперсии доходности портфеля (функции риска).
x1,x2,x3,x4,x5,x6,x7,x8,p,q,w=symbols(' x1 x2 x3 x4 x5 x6 x7 x8 p q w' , float= True)
v1=Matrix([x1,x2,x3,x4,x5,x6])
v2=v1.T
w=0
for i in np.arange(0,m):
for j in np.arange(0,n): w=w+v1[p.subs({p:i}),q.subs({q:0})]*v2[p.subs({p:0}),q.subs({q:j})]*CV[p.subs({p:i}),q.subs({q:j})]
print("Дисперсия доходности портфеля (функция риска):n%s"%w) Получим:
Дисперсия доходности портфеля (функция риска):
2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6 + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2 + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6 + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2
4. Определение оптимального портфеля акций для минимального риска и доходности mp=13.25
def objective(x):#функция риска
x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5]
return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6
+ 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2
+ 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6
+ 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2
def constraint1(x):#условие для суммы долей -1
return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0
def constraint2(x): # задание доходности
return d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5] - 13.25
x0=[1,1,0,0,0,1]#начальное значение переменных для поиска минимума функции риска
b=(0.0,1.0)# условие для x от нуля до единицы включая пределы
bnds=(b,b,b,b,b,b)#передача условий в функцию риска(подготовка)
con1={'type':'ineq','fun':constraint1} #передача условий в функцию риска(подготовка)
con2={'type':'eq','fun':constraint2} #передача условий в функцию риска(подготовка)
cons=[con1,con2]#передача условий в функцию риска(подготовка)
sol=minimize(objective,x0,method='SLSQP',
bounds=bnds,constraints=cons)# поиск минимума функции риска
print("Минимум функции риска -%s"%str(round(sol.fun,3)))
print("Акция 1 доля- %s, доходность- %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3)))
print("Акция 2 доля- %s, доходность- %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3)))
print("Акция 3 доля- %s, доходность- %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3)))
print("Акция 4 доля- %s, доходность- %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3)))
print("Акция 5 доля- %s, доходность- %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3)))
print("Акция 6 доля- %s, доходность- %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
Получим:
Минимум функции риска -1.846
Акция 1 доля- 0.141, доходность- 1.721
Акция 2 доля- 0.73, доходность- 9.616
Акция 3 доля- 0.0, доходность- 0.0
Акция 4 доля- 0.0, доходность- 0.0
Акция 5 доля- 0.0, доходность- 0.0
Акция 6 доля- 0.129, доходность- 1.914
Вывод:
Доходными являются 1,2,6 акции. Это и есть часть ответа на вопросы, поставленные в начале публикации.
from sympy import *
import numpy as np
from scipy.optimize import minimize
"D- матрица доходности(обычно загружается из файла)"
D=np.array([[9.889, 11.603,11.612, 12.721,11.453,12.102],
[12.517, 13.25,12.947,12.596,12.853,13.036],
[12.786, 12.822,15.447,14.452,15.143,16.247],
[11.863, 12.114,13.359,13.437,11.913,15.300],
[11.444, 13.292,13.703,11.504,13.406,15.255],
[14.696, 15.946,16.829,17.698,16.051,17.140]],np.float64)
d= np.zeros([6,1])# столбец для средней доходности
m,n= D.shape#размерность матрицы
for j in np.arange(0,n):
for i in np.arange(0,m):
d[j,0]=d[j,0]+D[i,j]
d=d/n
print("Средняя доходность по столбцам : n %s"%d)
CV= np.zeros([m,n])
for i in np.arange(0,m):
for j in np.arange(0,n):
x=np.array(D[0:m,j]).T
y=np.array(D[0:m,i]).T
X = np.vstack((x,y))
CV[i,j]=round(np.cov(x,y,ddof=0)[1,0],3)
print("Ковариационная матрица CV: n %s"%CV)
x1,x2,x3,x4,x5,x6,x7,x8,p,q,w=symbols(' x1 x2 x3 x4 x5 x6 x7 x8 p q w' , float= True)
v1=Matrix([x1,x2,x3,x4,x5,x6])
v2=v1.T
w=0
for i in np.arange(0,m):
for j in np.arange(0,n):
w=w+v1[p.subs({p:i}),q.subs({q:0})]*v2[p.subs({p:0}),q.subs({q:j})]*CV[p.subs({p:i}),q.subs({q:j})]
print("Дисперсия доходности портфеля (функция риска):n%s"%w)
def objective(x):#функция риска
x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5]
return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6
+ 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2
+ 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6
+ 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2
def constraint1(x):#условие для суммы долей -1
return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0
def constraint2(x): # задание доходности
return d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5] - 13.25
x0=[1,1,0,0,0,1]#начальное значение переменных для поиска минимума функции риска
b=(0.0,1.0)# условие для x от нуля до единицы включая пределы
bnds=(b,b,b,b,b,b)#передача условий в функцию риска(подготовка)
con1={'type':'ineq','fun’: constraint1} #передача условий в функцию риска(подготовка)
con2={'type':'eq','fun’: constraint2} #передача условий в функцию риска(подготовка)
cons=[con1,con2]#передача условий в функцию риска(подготовка)
sol=minimize(objective,x0,method='SLSQP',
bounds=bnds,constraints=cons)# поиск минимума функции риска
print("Минимум функции риска -%s"%str(round(sol.fun,3)))
print("Акция 1 доля- %s, доходность- %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3)))
print("Акция 2 доля- %s, доходность- %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3)))
print("Акция 3 доля- %s, доходность- %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3)))
print("Акция 4 доля- %s, доходность- %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3)))
print("Акция 5 доля- %s, доходность- %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3)))
print("Акция 6 доля- %s, доходность- %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
Оптимальный портфель Марковица максимальной доходности и заданного, (приемлемого) риска
Система уравнений и неравенств имеет вид:
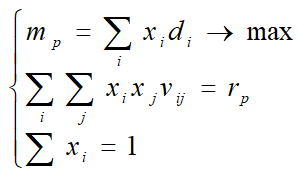
import numpy as np
from scipy.optimize import minimize
d=np.array( [[ 12.19916667],
[ 13.17116667],
[ 13.98283333],
[ 13.73466667],
[ 13.46983333],
[ 14.84666667]])
def constraint2(x):
x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5]
return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5
+ 3.95*x1*x6 + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6
+ 2.901*x3**2 + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5
+ 4.63*x4*x6 + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2-2
def constraint1(x):
return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0
def objective(x):
return -(12.199*x[0] + 13.171*x[1] + 13.983*x[2] + 13.735*x[3] + 13.47*x[4]+ 14.847*x[5] )
x0=[1,1,1,1,1,1]
b=(0.0,1.0)
bnds=(b,b,b,b,b,b)
con1={'type':'ineq','fun':constraint1}
con2={'type':'eq','fun':constraint2}
cons=[con1,con2]
sol=minimize(objective,x0,method='SLSQP',
bounds=bnds,constraints=cons)
print("Максимум функции доходности -%s"%str(round(sol.fun,3)))
print("Акция 1 доля- %s, доходность- %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3)))
print("Акция 2 доля- %s, доходность- %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3)))
print("Акция 3 доля- %s, доходность- %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3)))
print("Акция 4 доля- %s, доходность- %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3)))
print("Акция 5 доля- %s, доходность- %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3)))
print("Акция 6 доля- %s, доходность- %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
Часть приведенного листинга не требует пояснений, поскольку всё подробно изложено в предыдущем примере. Однако есть отличия. Столбец средней доходности d и функция условия def constraint2(x) взяты из предыдущего примера, причем в предыдущем примере это была функция минимального риска. Кроме того, для определения максимума перед выводом значения новой функции цели – def objective(x), поставлен знак минус.
Результат:
Максимум функции доходности --14.1
Акция 1 доля- 0.0, доходность- 0.0
Акция 2 доля- 0.72, доходность- 9.489
Акция 3 доля- 0.0, доходность- 0.0
Акция 4 доля- 0.0, доходность- 0.0
Акция 5 доля- 0.0, доходность- 0.0
Акция 6 доля- 0.311, доходность- 4.611
Акции 2,6 доходны. Но это не единственный результат оптимизации средствами scipy optimize minimize. Я решил сравнить результаты с решением той же задачи средствами Mathcad и вот что получил:

Mathcad указывает на те же номера 2,6 доходных акций, но доли другие. В Python 0.720,0.311 в Mathcad 0.539, 0.461, при этом разные значения максимальной доходности соответственно 14.1 и 13.9. Для того чтобы окончательно убедиться какая программа вычисляет оптимум правильно, подставим полученные в Python значения долей в Mathcad, получим:

Вывод: на Python оптимум функции, а следовательно доли и доходность вычисляется более точно, чем при использовании Mathcad.
Формирование оптимального портфеля ценных бумаг по модели Тобина
Портфель Тобина минимального риска:
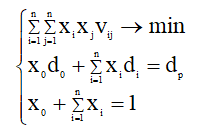
где d0 – эффективность без рисковых бумаг;
x0 – доля капитала вложенная в без рисковые бумаги;
xi,xj — доля капитала вложенная в ценные бумаги i-го и j–го видов;
di – математическое ожидание (среднее арифметическое) доходности i — й ценной бумаги;
vij – корреляционный момент между эффективностью бумаг i-го и j –го видов.
Подбираем долю капитала заданной доходности, задаём общую доходность, приняв для примера следующие числовые значения x0=0.3, d0 =10, dp=12.7.
import numpy as np
from scipy.optimize import minimize
d=np.array( [[ 12.19916667],
[ 13.17116667],
[ 13.98283333],
[ 13.73466667],
[ 13.46983333],
[ 14.84666667]])
x00=0.3;d0=10;dp=12.7
def objective(x):#функция риска
x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5]
return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6
+ 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2
+ 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6
+ 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2
def constraint1(x):#условие для суммы долей -1
return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0+x00
def constraint2(x): # задание доходности
return d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5] - dp+x00*d0
x0=[1,1,1,1,1,1]#начальное значение переменных для поиска минимума функции риска
b=(-1.0,100.0)# условие для x от нуля до единицы включая пределы
bnds=(b,b,b,b,b,b)#передача условий в функцию риска(подготовка)
con1={'type':'ineq','fun':constraint1} #передача условий в функцию риска(подготовка)
con2={'type':'eq','fun':constraint2} #передача условий в функцию риска(подготовка)
cons=[con1,con2]#передача условий в функцию риска(подготовка)
sol=minimize(objective,x0,method='SLSQP',
bounds=bnds,constraints=cons)# поиск минимума функции риска
print("Минимум функции риска : %s"%str(round(sol.fun,3)))
print("Акция 1 доля- %s, доходность: %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3)))
print("Акция 2 доля- %s, доходность: %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3)))
print("Акция 3 доля- %s, доходность: %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3)))
print("Акция 4 доля- %s, доходность: %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3)))
print("Акция 5 доля- %s, доходность: %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3)))
print("Акция 6 доля- %s, доходность: %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
Получим:
Минимум функции риска: 0.728
Акция 1 доля- -0.023, доходность: -0.286
Акция 2 доля- 0.666, доходность: 8.778
Акция 3 доля- -1.0, доходность: -13.983
Акция 4 доля- 0.079, доходность: 1.089
Акция 5 доля- 0.3, доходность: 4.048
Акция 6 доля- 0.677, доходность: 10.054
Доходными являются акции 2,4,5,6.
Портфель Тобина максимальной эффективности
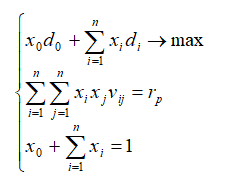
где rp – риск портфеля.
import numpy as np
from scipy.optimize import minimize
x00=0.8;d0=10;rp=0.07
d=np.array( [[ 12.19916667],
[ 13.17116667],
[ 13.98283333],
[ 13.73466667],
[ 13.46983333],
[ 14.84666667]])
def constraint2(x):
x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5]
return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5
+ 3.95*x1*x6 + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6
+ 2.901*x3**2 + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5
+ 4.63*x4*x6 + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2-rp
def constraint1(x):
return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0+x0
def objective(x):
return -(d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5]+x00*d0)
x0=[1,1,1,1,1,1]
b=(-1.0,100.0)
bnds=(b,b,b,b,b,b)
con1={'type':'ineq','fun':constraint1}
con2={'type':'eq','fun':constraint2}
cons=[con1,con2]
sol=minimize(objective,x0,method='SLSQP',
bounds=bnds,constraints=cons)
print("Максимум функции доходности : %s"%str(round(sol.fun,3)))
print("Акция 1 доля- %s, доходность: %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3)))
print("Акция 2 доля- %s, доходность: %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3)))
print("Акция 3 доля- %s, доходность: %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3)))
print("Акция 4 доля- %s, доходность: %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3)))
print("Акция 5 доля- %s, доходность: %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3)))
print("Акция 6 доля- %s, доходность- %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
Получим:
Максимум функции доходности: -11.657
Акция 1 доля- 0.09, доходность: 1.096
Акция 2 доля- 0.196, доходность: 2.583
Акция 3 доля- -1.0, доходность: -13.983
Акция 4 доля- 0.113, доходность: 1.552
Акция 5 доля- 0.411, доходность: 5.538
Акция 6 доля- 0.463, доходность- 6.872
Доходными являются акции 1,2,4,5.
Выводы:
Впервые средствами Python решена задача оптимизации портфеля ценных бумаг по моделям Марковица и Тобина.
На сравнительном примере c математическим пакетом Mathcad показаны преимущества библиотеки scipy optimize minimize.
Ссылки:
- Символьное решение задач нелинейного программирования
- scipy.optimize.minimize
- Постановка задачи об оптимальном портфеле
Автор: Scorobey






