Часть первая — Affinity propagation
Часть вторая — DBSCAN
Часть третья — кластеризация временных рядов
Часть четвёртая — SOM
Self-organizing maps (SOM, самоорганизующиеся карты Кохонена) — знакомая многим классическая конструкция. Их часто поминают на курсах машинного обучения под соусом «а ещё нейронные сети умеют вот так». SOM успели пережить взлёт в 1990-2000 годах: тогда им пророчили большое будущее и создавали новые и новые модификации. Однако, в XXI веке SOM понемногу уходят на задний план. Хоть новые разработки в сфере самоорганизующихся карт всё ещё ведутся (большей частью в Финляндии, родине Кохонена), даже на родном поле визуализации и кластеризации данных карты Кохонена всё чаще уступает t-SNE.
Давайте попробуем разобраться в тонкостях SOM'ов, и выяснить, заслуженно ли они были забыты.

Основные идеи алгоритма
Вкратце напомню стандартный алгоритм обучения SOM[1]. Здесь и далее 













Также обратите внимание, что хоть нейроны часто для удобства рисуются так, будто бы они «нанизаны» на квадратную сетку, это совсем не означает, что и хранятся они как тензор 

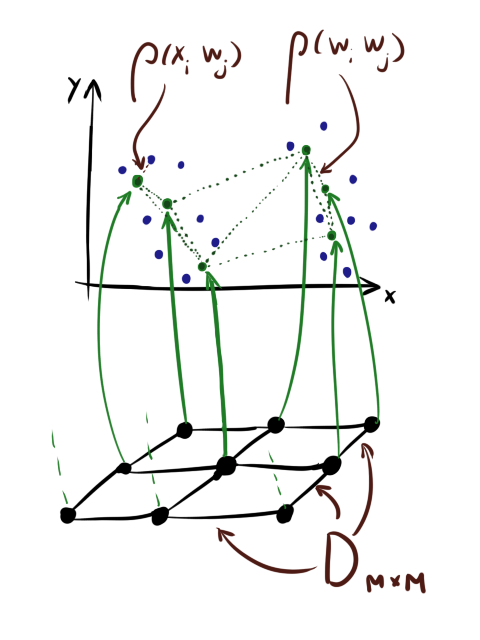
Введём сразу 

Алгоритм 1 (стандартный алгоритм обучения SOM):
Вход: 





- Инициализировать
раз:
- Перемешать список индексов случайным образом order: = shuffle(
)
- Для каждого
из order:
// Берём случайный вектор из X
// Находим номер ближайшего к нему нейрона
// Находим коэффициент близости нейронов по сетке. Pаметьте, что
всегда 1
:=
:=
- Перемешать список индексов случайным образом order: = shuffle(
Каждую эпоху обучения мы перебираем элементы входного датасета. Для каждого элемента мы находим ближайший к этому 




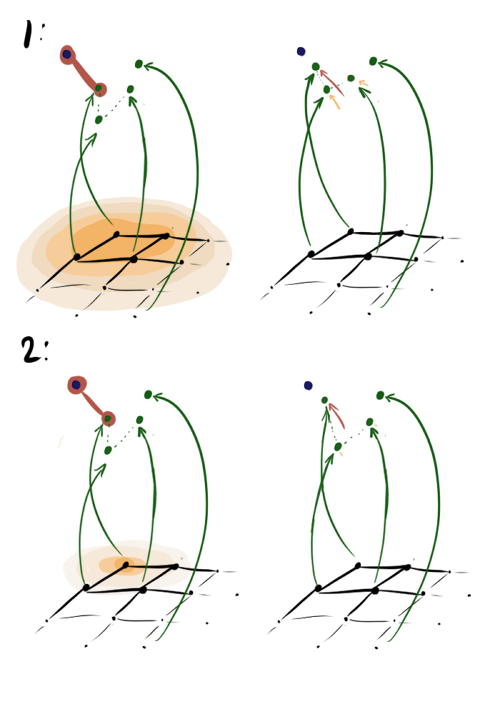
В первом случае 



Несколько эпох обучения карты Кохонена для наглядности:
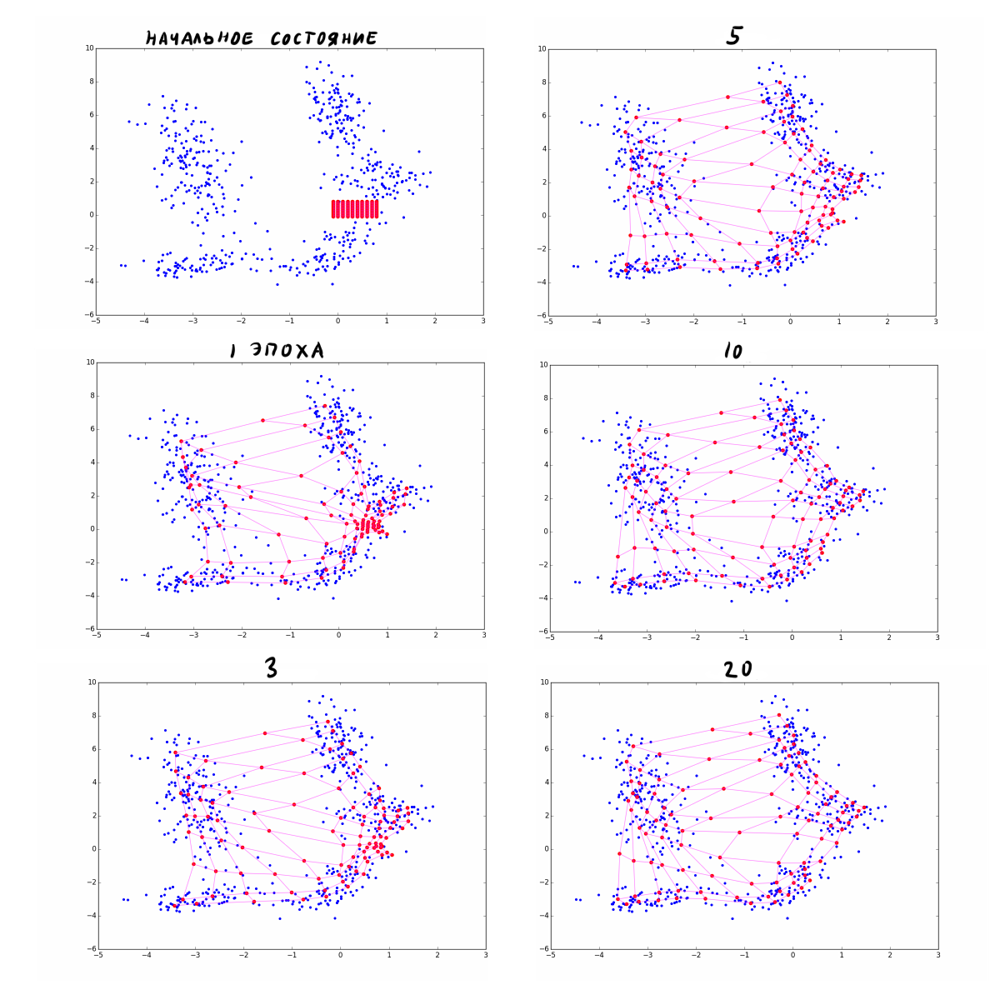
Если моего краткого напоминания алгоритма оказалось недостаточно, прочитайте эту статью, где шаги в А1 рассмотрены более подробно.
Таким образом, основные идеи SOM:
- Принудительное внедрение некоторого порядка между нейронами.
мягко переносится на
, в пространство данных.
- Стратегия Winner Takes All (WTA). На каждом шаге обучения мы определяем ближайший «победивший» нейрон и исходя из этого знания обновляем веса.
- Кооперация перерастает в эгоизм
глобальная примерная подстройка перерастает в точную локальную. Пока
большая, обновляется заметная часть
и стратегия WTA не так видна, когда
стремится к нулю,
обновляются по одному.
Сразу напрашивается несколько тривиальных модификаций:
- Не обязательно использовать гауссиану для вычисления
на шаге А1.2.2.3. Первый кандидат в альтернативные варианты — распределение Коши. Как известно, оно имеет более тяжёлые хвосты: больше нейронов будут изменяться на этапе кооперации.
- Затухания
и
не обязаны быть экспоненциальными. Кривая затухания в виде сигмоиды или ветви гауссианы может дать алгоритму больше времени для грубой подстройки.
- Не обязательно крутиться в цикле именно
раз. Можно прекращать итерации, если значения W не будут меняться на протяжении нескольких эпох.
- Обучение напоминает обычный SGD. «Напоминает», потому что не существует какой-либо функции энергии, которую бы этот процесс оптимизировал[2]. Строгую математику нам портит шаг А1.2.2.1 — взятие ближайшего вектора. Существуют модификации SOM, где энергия таки есть, но мы и так вдаёмся в детали. Смысл в том, что это не мешает использовать на шаге А1.2.2.4 вместо обычных обновлений весов, скажем, импульс Нестерова (Nesterov momentum).
- Добавление небольших случайных пертурбаций в градиент хоть и приносит меньшую пользу, чем в случае обычных многослойных нейронных сетей, всё равно выглядит полезным приёмом для избегания седловых точек[3].
- Self-organizing maps поддерживают обучение подвыборками (batches)[1]. Их применение позволяет проводить обучение быстрее и глаже проскакивать плохие конфигурации
- Не забывайте про нормализацию входных значений и использование вектора весов входных переменных, если известно, что какие-то фичи важнее других.
Топология нейронов
Чуть менее очевидная модификация самоорганизующихся карт, в которой состоит их сила и уникальность, но про которую постоянно забывают, кроется в этапе инициализации 


Как минимум, вместо обычной сетки лучше использовать гексагональную: квадратная сетка искажает результаты в пользу прямых линий, да и менее приятна на вид чем шестиугольная. Если предполагается, что данные циклические, стоит инициализировать 

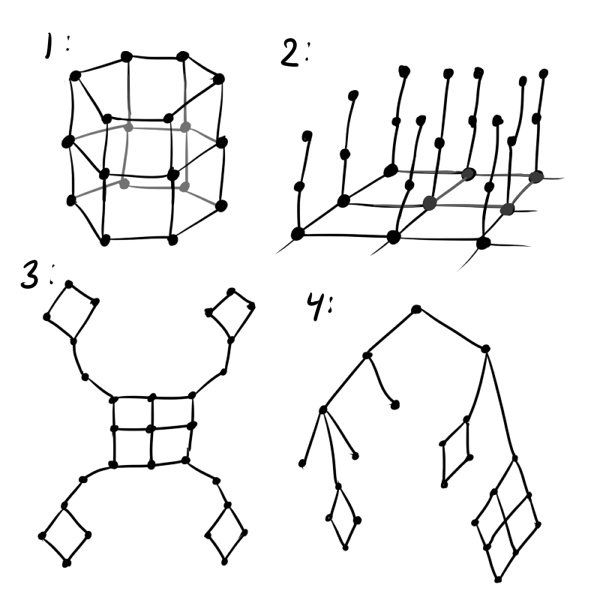
В общем, 




Абстрактный пример классического перекрута:
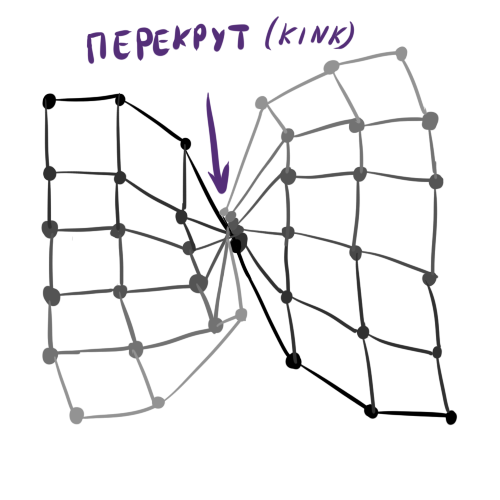
Пример перекрута на синтетических данных при попытке вписать длинную кривую в кластеры. Верхний левый и правый лепестки выглядят правдоподобно, но выделенное место портит порядок.
Инициализируя веса в слое случайным образом, вы практически гарантируете себе плохой результат на выходе. Необходимо сконструировать 
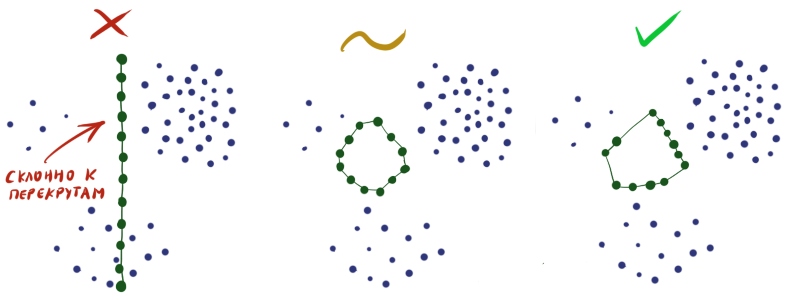
Поэтому часто приходится делать так, чтобы нейроны просто равномерно рассеялись по всему пространству данных без пересечений (как на рисунке посередине), и мириться с тем, что не во всех областях плотность нейронов будет отвечать плотности данных.
Winner relaxation/winner enhancing
Эта идея была изначально предложена Кохоненом[1], а затем обобщена его последователями[4]. Что если отнимать или прибавлять к обновлению нейрона-победителя обновления его соседей? Математически это выглядит так: шаг А1.2.2.4 для нейрона победителя заменяется на
Где 


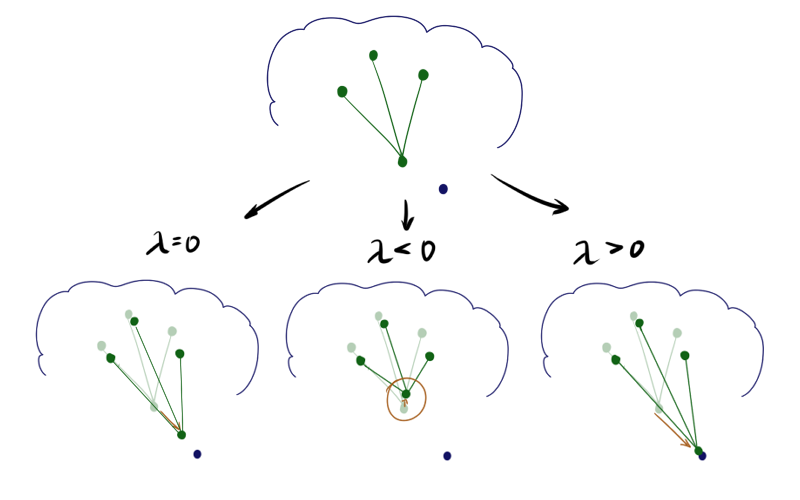
При отрицательном 

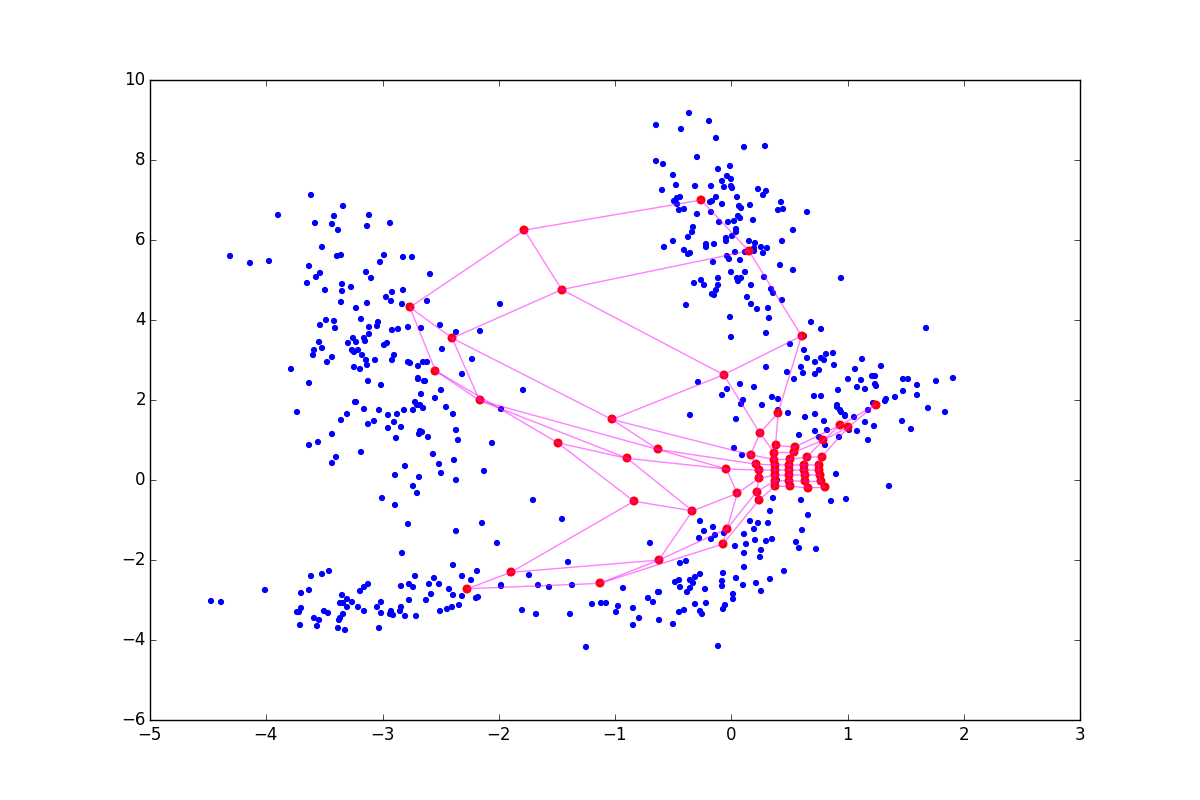
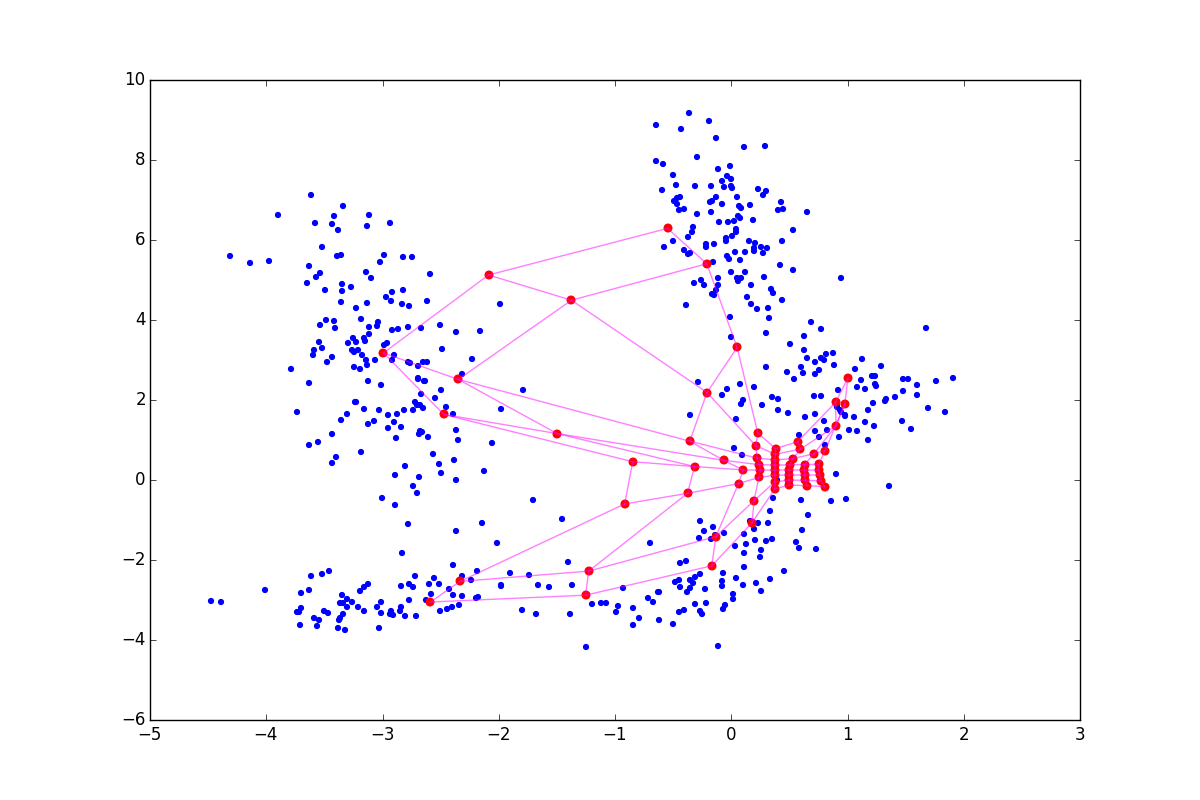
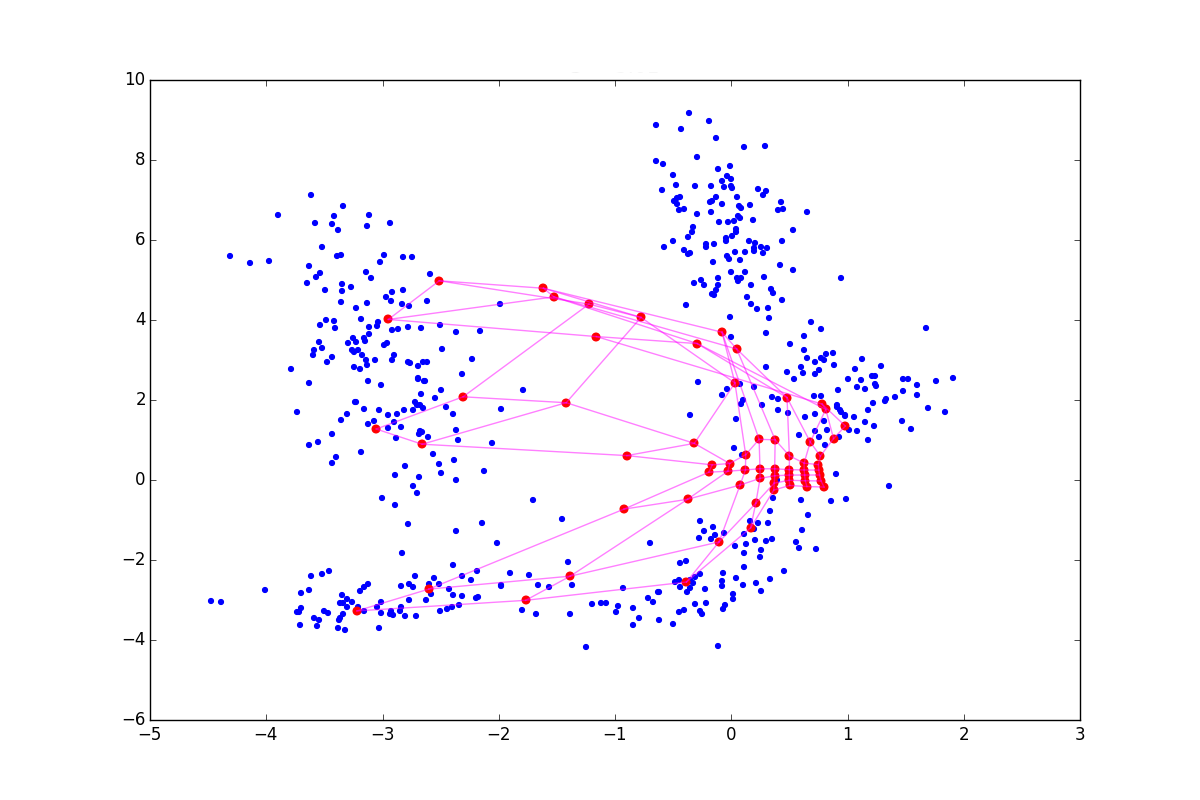
Из-за описанных выше эффектов 

![Нестандартная кластеризация 4: Self-Organizing Maps, тонкости, улучшения, сравнение с t-SNE - 92 $lambda in [-1; 1]$](https://www.pvsm.ru/images/2017/10/13/nestandartnaya-klasterizaciya-4-Self-Organizing-Maps-tonkosti-uluchsheniya-sravnenie-s-t-SNE-92.svg)


Cluster refinement phase
Часто случается так, что после основного цикла алгоритма оказывается, что хоть нейроны SOM и прицепились к чему-то, их плотность на кластерах вполне сравнима с плотностью в местах, где кластеров нет. Проводить анализ в таких условиях довольно сложно. Нарни Манукьян и команда предлагают[5] довольно простое решение: вслед за основным алгоритмом запускать ещё один цикл подгонки нейронов.
Алгоритм 2, Cluster refinement phase (фаза подстройки кластеров):
Вход: 




раз:
- Перемешать список индексов случайным образом order: = shuffle(
)
- Для каждого
из order:
// Берём случайный вектор из X
// Находим коэффициент близости нейронов к выбранному элементу данных
:=
:=
- Перемешать список индексов случайным образом order: = shuffle(
Хоть алгоритм выглядит и очень похоже на А1, обратите внимание, что теперь мы не ищем ближайший нейрон, а просто пододвигаем все нейроны к 



Аккуратнее: чем сильнее подстройка в CR-фазе, тем лучше видны кластеры, но тем больше теряется локальная информация о форме кластера. После нескольких эпох остаются только данные о вытянутости сгустков. CR может схлопнуть несколько складок находящихся рядом, а при слишком большой 
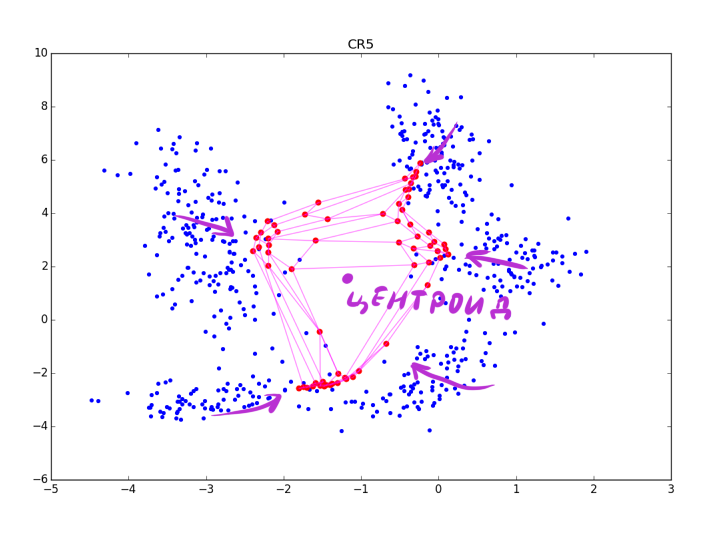
Впрочем, последнюю проблему можно избежать, если взять вместо экспоненты какую-нибудь функцию, которая после некоторого максимального значения обращается в 0.
Авторы статьи советуют использовать вместо отдельного параметра скорости обучения ту же 

Визуализация, Rectifying SOM
Пока что я не сказал ни слова именно о кластеризации данных при помощи SOM. Построенная при помощи 

Самый простой способ определения количества сгустков данных на складке — вдумчивое вглядывание в так называемую U-матрицу. Это разновидность визуализации карт Кохонена, где вместе со значениями нейронов показывается расстояние между ними. Таким образом можно легко можно определить, где кластеры соприкасаются, а где проходит граница.
Более интересный способ — запустить поверх получившейся матрицы 


Но более продвинутым кажется накапливание релевантной информации о кластерах прямо во время работы основного алгоритма. Эрен Голге и Пинар Дайгулу предлагают[6] каждую эпоху работы основного алгоритма запоминать, сколько раз активировался нейрон (т.е. нейрон оказывался победителем или его вес обновлялся, т.к. победителем оказывался близкий по слою нейрон), и на основании этого судить, олицетворяет ли нейрон кластер или повис в пустом пространстве.
Алгоритм 3, Rectifying SOM (А1 с изменениями):
Вход: 




- Инициализировать
- Инициализировать
// Excitement score — полный счёт возбуждения нейрона
раз:
- Инициализировать
// Win count — счёт возбуждения нейрона в текущую эпоху
- Перемешать список индексов случайным образом order: = shuffle(
)
- Для каждого
из order:
// Берём случайный вектор из X
// Находим номер ближайшего к нему нейрона
// Находим коэффициент близости нейронов по сетке. Pаметьте, что
всегда 1
// Обновляем текущий счёт активации
:=
:=
// Накапливаем общий счёт
- Инициализировать
Чем чаще нейрон оказывается победителем, тем больше вероятность, что он где-то в толще кластера, а не вне её. Обратите внимание, что полный счёт нейронов накапливается с множителем 
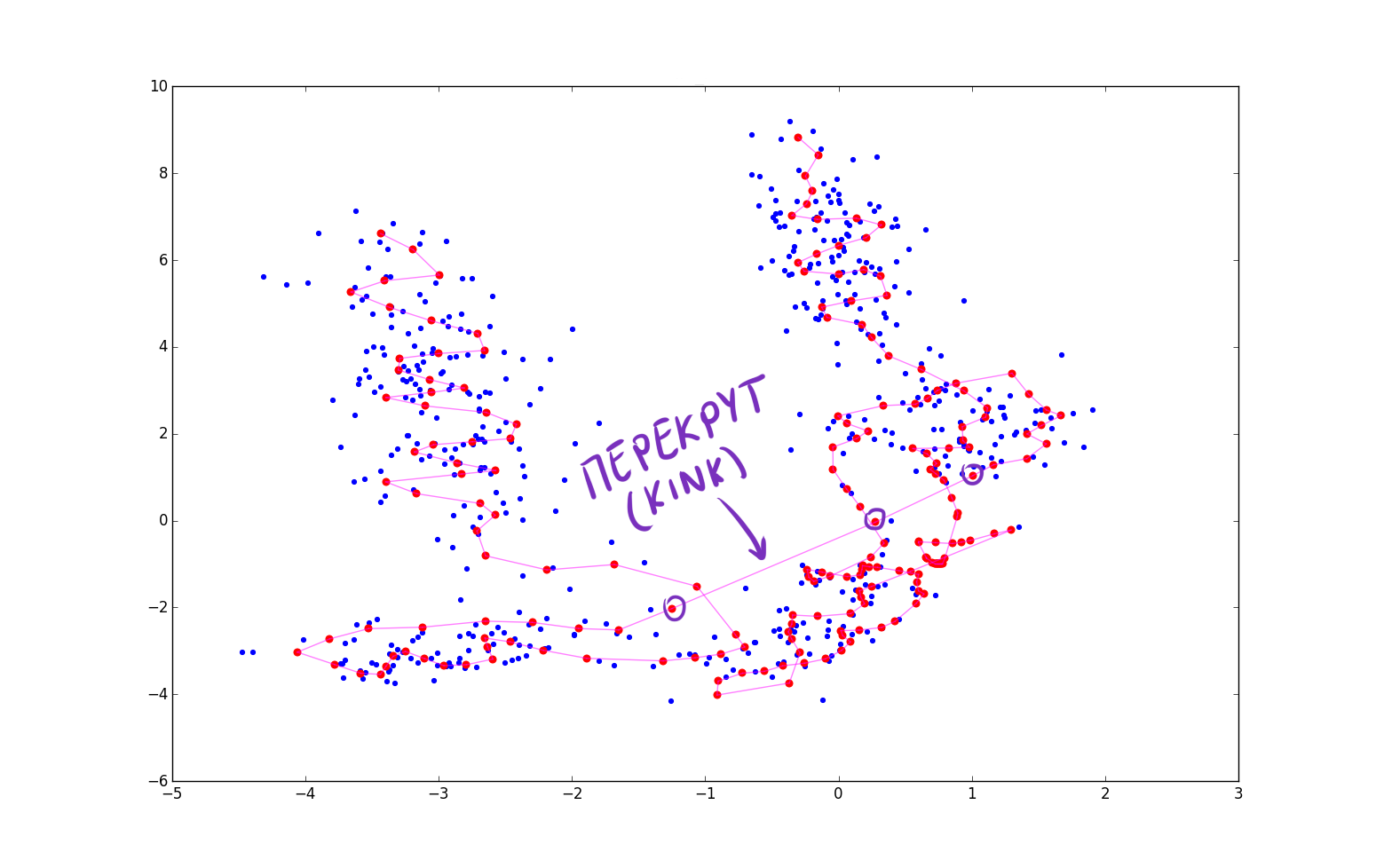
ES — безразмерная величина, её абсолютные значения не несут особого смысла. Просто чем больше значение, тем больше шансов, что нейрон прицепился к чему-то значимому. После окончания А3 следует как-либо нормализовать получившийся вектор. После наложения ES на нейроны получится примерно такая картина:
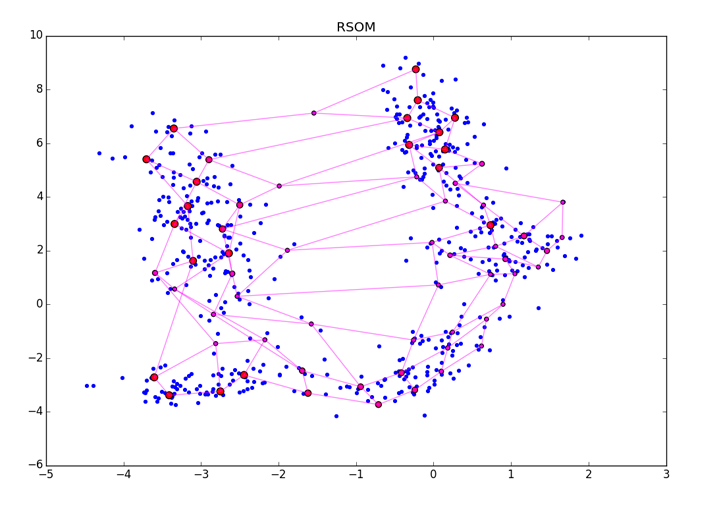
Крупные красные точки представляют нейроны с высоким счётом возбуждения, маленькие красно-фиолетовые — с малым. Обратите внимание, что RSOM чувствителен ко способу финальной обработки ES и к кластерам разной плотности в данных (см. нижний правый угол картинки). Убедитесь, что вы задали больше эпох чем нужно для сходимости алгоритма, чтобы ES точно успел накопить правильные значения.
Лучше всего, разумеется, применять и RSOM, и дополнительный кластеризатор поверх и просмотр визуализации глазами.
Прочее
В обзор не вошли
- Модификации SOM для работы с категориальными данными[7], последовательностями, картинками и прочими, неродными для SOM, видами данных[1].
- Работы связанные со временной асимметричностью функций близости нейронов по сетке.
Автор утверждает, что это позволяет бороться с перекрутами[8]. - Исследования, связанные с контролем над степенью покрытости данных нейронами (борьба с искажениями на краях датасета)[9].
- Накопление информации о важности определённых входов[10].
- Кодирование данных при помощи SOM[1].
- Хитрые способы инициализации
[11][12].
- Возможность добавить дополнительное слагаемое упругости. Упругость служит аналогом регуляризации в обычных нейронных сетях, запрещая слишком запутанные конфигурации.
- Многие другие интересные, но слишком специальные вещи.
Сравнение SOM и t-SNE
| SOM | t-SNE | |
|---|---|---|
| Сложность |  |
Barnes-Hut t-SNE —  , но другие реализации могут быть более вычислительноёмкими , но другие реализации могут быть более вычислительноёмкими |
| Количество гиперпараметров | 3-5, возможно намного больше + матрица расстояний на нейронах. Обязательны количество эпох, learning rate и начальный коэффициент сотрудничества. Также часто указываются затухание скорости обучения и коэффициент сотрудничества, но с ними почти никогда не возникает проблем. | 3-4, возможно больше + метрика на данных. Обязательны количество эпох, learning rate и perplexity, часто встречается early exaggeration. Perplexity довольно магический, однозначно придётся с ним повозиться. |
| Разрешение результирующей визуализации | Элементов не больше, чем нейронов ( ) ) |
Элементов не больше, чем элементов в наборе данных ( ) ) |
| Топология визуализации | Любая, нужно лишь предоставить матрицу расстояний между нейронами | Только обычная плоскость или трёхмерное пространство |
| Дообучение, расширение структуры | Есть, довольно тривиально реализовать | Нет |
| Поддержка дополнительных слоёв преобразований | Есть, можно поставить перед слоем Кохонена сколько угодно плотносоединённых или свёрточных слоёв и обучить обычным backprop'ом | Нет, только ручное преобразование данных и feature-engeneering |
| Предпочитаемые типы кластеров | По умолчанию отлично отображает кластеры в виде двумерных складок и экзотические кластеры. Нужны ухищрения, чтобы хорошо визуализировать структуры с размерностью больше двух. | Замечательно отображает гипершары. Гиперскладки и экзотические чуть хуже, сильно зависит от функции расстояния. |
| Предпочитаемая размерность пространства данных | Зависит от данных, но чем больше, тем хуже. Алгоритм может деградировать даже при  , так как у гиперскладки, образованной нейронами появляется слишком много степеней свободы. , так как у гиперскладки, образованной нейронами появляется слишком много степеней свободы. |
Любая, пока не начнёт сказываться проклятие размерности |
| Проблемы с начальными данными | Нужно инициализировать веса нейронов. Это может быть технически сложно в случае нестандартной матрицы расстояний между нейронами (особенно топологии типа «граф») | Нет |
| Проблемы с выбросами | Есть, особенно если они распределены неравномерно | Нет, на визуализации они тоже будут выбросами |
| Эффекты на краях распределения данных | Часть данных остаётся недопокрытой SOM | Почти незаметны |
| Проблемы с ложноположительными кластерами | Нет | Ещё какие |
| Размер кластеров в визуализации | Несёт смысловую нагрузку | Почти всегда ничего не значит |
| Расстояние между кластерами в визуализации | Несёт смысловую нагрузку | Часто ничего не значит |
| Плотность кластеров в визуализации | Обычно имеет смысловую нагрузку, но может вводить в заблуждение в случае плохой инициализации | Часто ничего не значит |
| Форма кластеров в визуализации | Несёт смысловую нагрузку | Может обманывать |
| Как сложно оценить качество кластеризации | Очень сложно :( | Очень сложно :( |
Казалось бы, SOM выигрывает по вычислительной сложности, однако не стоит радоваться раньше времени, не увидев 




В приведённой таблице видны сильные и слабые стороны SOM и t-SNE. Легко можно понять, почему самоорганизующиеся карты уступили место другим методам кластеризации: хоть визуализация картами Кохонена более осмыслена, позволяет наращивание новых нейронов и задание желаемой топологии на нейронах, деградация алгоритма при большом 

Значит ли это, что самоорганизующиеся карты остались в прошлом data science? Не совсем. Нет-нет, да и приходится иногда обрабатывать не очень многомерные данные — для этого вполне можно воспользоваться SOM. Визуализации получаются действительно довольно красивые и эффектные. Если не лениться применять доработки алгоритма, SOM отлично находит кластеры на гиперскладках.
Спасибо за внимание. Надеюсь, моя статья вдохновить кого-нибудь на создание новых SOM-визуализаций. С гитхаба можно скачать код с минимальным примером SOM с основными оптимизациями, предложенными в статье и посмотреть на анимированное обучение карты. В следующий раз я постараюсь рассмотреть алгоритм «нейронный газ», который также основан на конкурентном обучении.
[1]: Self-Organizing Maps, book; Teuvo Kohonen
[2]: Energy functions for self-organizing maps; Tom Heskesa, Theoretical Foundation SNN, University of Nijmegen
[3]: bair.berkeley.edu/blog/2017/08/31/saddle-efficiency
[4]: Winner-Relaxing Self-Organizing Maps, Jens Christian Claussen
[5]: Data-Driven Cluster Reinforcement and Visualization in Sparsely-Matched Self-Organizing Maps; Narine Manukyan, Margaret J. Eppstein, and Donna M. Rizzo
[6]: Rectifying Self Organizing Maps for Automatic Concept Learning fromWeb Images; Eren Golge & Pinar Duygulu
[7]: An Alternative Approach for Binary and Categorical Self-Organizing Maps; Alessandra Santana, Alessandra Morais, Marcos G. Quiles
[8]: Temporally Asymmetric Learning Supports Sequence Processing in Multi-Winner Self-Organizing Maps
[9]: Magnification Control in Self-Organizing Maps and Neural Gas; Thomas Villmann, Jens Christian Claussen
[10]: Embedded Information Enhancement for Neuron Selection in Self-Organizing Maps; Ryotaro Kamimural, Taeko Kamimura
[11]: Initialization Issues in Self-organizing Maps; Iren Valova, George Georgiev, Natacha Gueorguieva, Jacob Olsona
[12]: Self-organizing Map Initialization; Mohammed Attik, Laurent Bougrain, Frederic Alexandre
Автор: Siarshai

























