Введение
В технике явление формирования поверхности вращающейся жидкости в форме близкой к поверхности параболоида вращения используется в основном в сепарирующих центрифугах для разделения суспензий на фракции [1].
Меня заинтересовал так называемый жидкостной тахометр. Принцип работы прибора состоит в контроле за уровнем верхней кромки жидкости во вращающемся цилиндрическом стакане.
Уровень жидкости зависит от скорости вращения стакана и может контролироваться простой оптической следящей системой.
Рассмотрение математической модели такого прибора имеет не только познавательный, но и практический интерес с учётом её реализации средствами свободно распространяемого языка общего назначения Python.
Теория – просто и кратко
Вектора сил, действующих на частицу жидкости во вращающемся цилиндрическом стакане приведены на следующем рисунке.
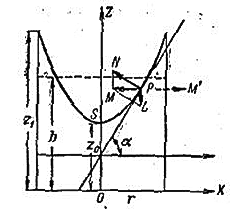
Рассмотрим сечение поверхности вращения координатной плоскостью ZX и найдём касательную в точке P (x, z) этого сечения. На частицу Q находящуюся в точке P действует сила тяжести mg изображённая в виде вектора PL.
Давление жидкости изображено в виде вектора PN направленного нормально к поверхности жидкости. Силы PM и PM’ для установившегося движения равны. Частица жидкости движется по окружности радиуса x её ускорение PM направлено к центру вращения и равно m*w**2 *x.
В приведенных формулах w, m, g – угловая частота, масса и ускорение свободного падения. В прямоугольном треугольнике NMP угол при вершине N равен производной dz/dx (при написании формул будем использовать синтаксис Python).
dz/dx=MP/NP= m*w**2 *x/mg= w**2 *x/g (1)
Интегрируя (1) получим уравнение для поверхности жидкости в сечении ZX. Для интегрирования (1) воспользуемся символьным вычислением неопределённого интеграла при помощи модуля SymPy:
from sympy import *
x,z,w,g = symbols('x z w g')
print('z=',integrate(w**2*x/g, x),'+C')Под “знаком” неопределённого интеграла integrate(f(x), x)– функция f(x)=w**2*x/g от переменной x. Остальные части равенства включая постоянную интегрирования C просто дописаны как строковые переменные.
Получим
z= w**2*x**2/(2*g) +C (2)
Постоянную интегрирования С определим подставив в (2) – x=0 и z=z0, получим C=z0. На верхней кромке вращающейся жидкости x=R, где R- радиус цилиндра, перепишем (2) в виде:
z-z0= w**2*R**2/(2*g) (3)
В неподвижном состоянии уровень жидкости равен H, а её объём V=pi*R**2*H. Когда жидкость начинает вращаться и после того как движение становиться установившемся объём жидкости не меняется, и он будет равен объёму, отсчитанному от верхней кромки жидкости – pi*R**2*z1 минус объём, занимаемый параболоидом вращения.
Этот объём равен произведению числа pi на определённый интеграл в пределах от z0 до z1 от соотношения x**2=2*g(z-z0)/w**2, полученного из (3) обратной подстановкой x=R.
Воспользуемся символьным вычислением определённого интеграла при помощи модуля SymPy:
from sympy import *
z,z0,z1,w,g = symbols('z z0 z1 w g')
print ('pi*R**2*H=pi*R**2*z1 -pi*', factor(simplify(integrate(2*g*(z-z0)/w**2,(z,z0,z1))))) Под “знаком” определённого интеграла integrate(f(z), (z, z0, z1))– функция f(z)= (2*g*(z-z0)/w**2 и кортеж – (z, z0, z1) с переменной z и пределами интегрирования–z0, z1. Функция simplify для упрощения выражения, а factor для сбора в полный квадрат. Остальные части равенства просто дописаны как строковые переменные.
Получим
pi*R**2*H=pi*R**2*z1 -pi* g*(z0 — z1)**2/w**2 (4)
После подстановки (3) в (4) получим:
H= (z1+z0)/2 (5)
Решив (3) относительно круговой частоты вращения w и исключив с учётом (5) переменную z0 получим уравнение теоретической характеристики водного тахометра:
w=2*sqrt (g*(z1-H))/R (6)
Соотношение (6) показывает только характер зависимости, реальную характеристику получают при градуировке.
Проймем R=0,11 м., H=0,09, построим теоретическую характеристику жидкостного тахометра для диапазона z1=0,1÷0,16.
from mpmath import *
w=lambda z1: 2*sqrt (9.8*(z1-0.09))/0.1
plot (w,[0.1,0.16])Использование функции mpmath упрощает визуализацию числовых данных.
Получим
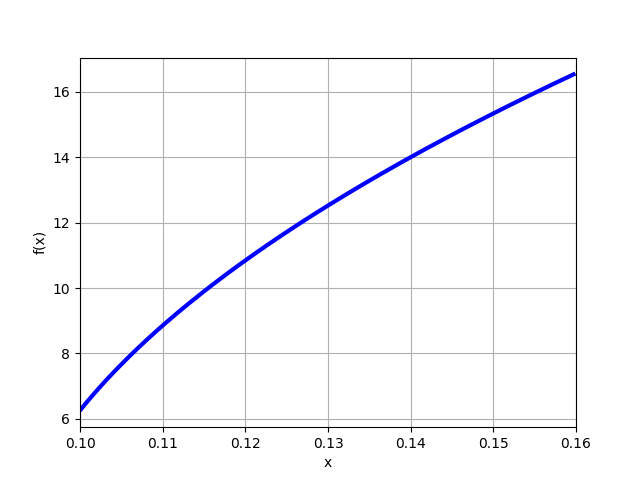
Модель жидкостного тахометра в 3D
Поверхность вращающейся жидкости можно описать параболоидом вращения. В общем случае — это эллиптический параболоид. Он определяется следующей зависимостью координат точек поверхности от двух параметров u и v:
x = a* u* cos v, y = b* u *cos v, z=0.5*u**2
В нашем случае жидкость находится в цилиндрическом стакане, поэтому a=b.
#!/usr/bin/env python
#coding=utf8
import pylab
from matplotlib import cm
from numpy import (zeros,arange,ones,pi,sin,cos)
from matplotlib.colors import LinearSegmentedColormap
from mpl_toolkits.mplot3d import Axes3D
def paraboloid():
a=2
v = arange(0, 2.05*pi, 0.05*pi)
u= zeros([len(v),1])
for i in arange(0,len(v)):
u[i,0]=list(arange(0,2.05,0.05))[i]
x=a*u*cos(v)
y=a*u*sin(v)
z=0.5*u**2*ones(len(v))
return x,y,z
x,y,z=paraboloid()
fig = pylab.figure()
axes = Axes3D(fig)
axes.plot_surface(x, y, z, rstride=1, cstride=1, cmap = cm.jet)
pylab.show()
Результат
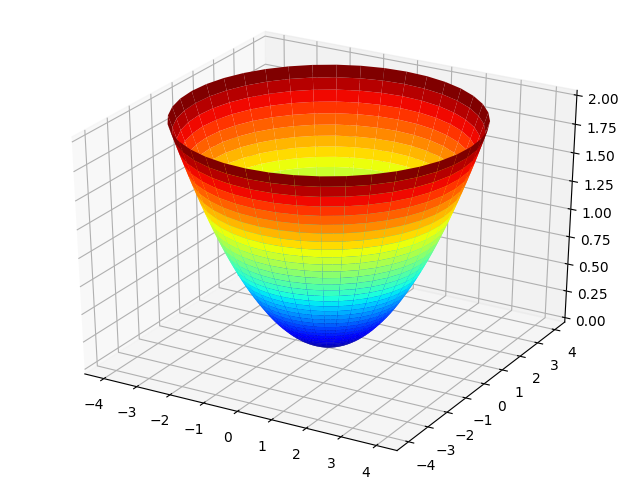
Поверхность цилиндра определяется следующей зависимостью координат точек поверхности от двух параметров u и v:
x = a* cos v, y =a*sin v, z = u
#!/usr/bin/env python
#coding=utf8
import pylab
from matplotlib import cm
from numpy import (zeros,arange,ones,pi,sin,cos)
from matplotlib.colors import LinearSegmentedColormap
from mpl_toolkits.mplot3d import Axes3D
def zilindr():
a=2
v = arange(0, 2.05*pi, 0.05*pi)
u= zeros([len(v),1])
for i in arange(0,len(v)):
u[i,0]=list(arange(0,2.05,0.05))[i]
x=a* cos(v)
y=a*sin(v)
z=u*ones(len(v))
return x,y,z
x,y,z=zilindr()
fig = pylab.figure()
axes = Axes3D(fig)
axes.plot_surface(x, y, z, rstride=1, cstride=1, cmap = cm.jet)
pylab.show()
Результат
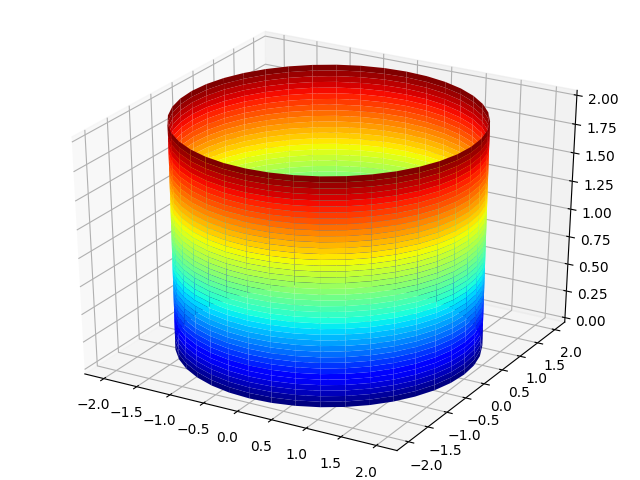
Разместим параболоид вращения в цилиндре, так чтобы верхняя кромка цилиндра совпадала с кромкой параболоида. При этом с ростом частоты вращения цилиндра уровень верхней кромки жидкости поднимается. Рассмотрим работу жидкостного тахометра. Введём коэффициент K, как характеристику скорости вращения жидкости, в следующую программу.
#!/usr/bin/env python
#coding=utf8
import pylab
from numpy import (zeros,arange,ones,pi,sin,cos)
from mpl_toolkits.mplot3d import Axes3D
def paraboloid(k):
a=2
v = arange(0, 2.05*pi, 0.05*pi)
u= zeros([len(v),1])
for i in arange(0,len(v)):
u[i,0]=list(arange(0,2.05,0.05))[i]
x=a*u*cos(v)
y=a*u*sin(v)
z=k*u**2*ones(len(v))
p=z[len(v)-1,len(v)-1]
a=2*a
u= zeros([len(v),1])
for i in arange(0,len(v)):
u[i,0]=list(arange(-2.1,2.1,0.1))[i]
X = a*ones(len(u))*cos(v)
Y =a*ones(len(u))*sin(v)
Z = u*ones(len(v))
q=Z[len(v)-1,len(v)-1]
d=p-q-0.1
Z = u*ones(len(v))+d
fig = pylab.figure(num='Форма поверхности жидкости во вращающемся цилиндре')
axes = Axes3D(fig)
axes.set_xlabel('x')
axes.set_ylabel('y')
axes.set_zlabel('z')
axes.plot_surface(x, y, z, rstride=1, cstride=1,color='red')
axes.plot_surface(X, Y, Z, rstride=1, cstride=1, color='blue')
pylab.show()
for k in arange(0.2,0.7,0.2):
print('k=',k)
paraboloid (k)
Для соединения цилиндра и параболоида вращения использованы следующие строки программы по переопределению координаты цилиндра Z по координате параболоида z:
q=Z[len(v)-1,len(v)-1]
d=p-q-0.1
Z = u*ones(len(v))+d Результат

k= 0.2
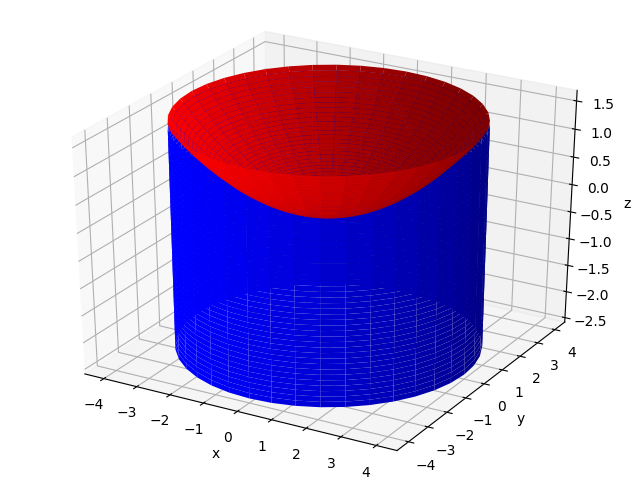
k= 0.4

k= 0.6
Кроме коэффициента K модель позволяет установить необходимый радиус цилиндра R и уровень жидкости в цилиндре H.
Выводы
Полученная математическая модель может найти применение не только при проектировании жидкостного тахометра, но и при разработке автоматического дозатора поскольку объём жидкости, вытесняемый параболоидом вращения может сливаться через отверстия в цилиндре. Кроме того, использование Python расширит область использования математической модели.
Ссылки
1.Центрифуга. Процесс центрифугирования.
Автор: Юрий Тараненко






