Как я сделал самый быстрый ресайз изображений. Часть 3, числа с фиксированной точкой

Я продолжаю подробно рассказывать о приемах оптимизации, позволивших мне написать самый быстрый ресайз изображений на современных x86 процессорах. На этот раз речь пойдет о преобразовании вычислений с плавающей точкой в вычисления с целыми числами. Сперва я расскажу немного теории, как это работает. Затем вернусь к реальному коду, в том числе SIMD-версии.

В предыдущих частях:

→ Часть 0
→ Часть 1, общие оптимизации
→ Часть 2, SIMD

Целые числа и плавающие точки

Думаю, все знают, что есть два основных способа представления чисел в памяти компьютера. Вот их основные особенности:

Целые числа

• Хранят точное значение
• Имеют относительно небольшой диапазон значений
• Разница между двумя соседними значениями всегда равна 1
• Удобны для хранения
• 1 – 0.1 = 0

Числа с плавающей точкой

• Хранят приблизительное значение с определенной точностью
• Диапазон значений очень большой
• Разница между соседними значениями может быть больше числа фотонов во вселенной
• Удобны для промежуточных вычислений
• 1 – 0.1 = 0.900000000000000022204460...

Числа с плавающей точкой хранятся в памяти в виде двух значений — мантиссы и экспоненты. Мантисса — это биты, которые хранят само значение (почти как целые числа), а экспонента говорит, на сколько разрядов сдвинуто значение мантиссы. Чтобы узнать истинное значение числа, нужно мантиссу умножить на разрядность в степени экспоненты: m·2ᵉ. Разрядность в данном случае 2, т.к. система счисления двоичная.

Кажется, что эта система достаточно сложная по сравнению с целочисленным представлением числа. Однако, на современных процессорах большинство операций (таких как умножение и сложение) над числами с плавающей точкой выполняется за такое же количество тактов, что и операции над целыми. Сложность операций приводит только к росту числа транзисторов в процессорах, но не количества тактов. Но помимо скорости самих операций, есть еще несколько факторов, которые нужно рассматривать в контексте производительности.

• Как сказано выше, целые числа чаще используются для хранения, а с плавающей точкой для вычислений. Это значит, что часто нужно конвертировать из одного представления в другое. Это конечно быстро, но в зависимости от задачи может влиять на производительность. В конце первой части я описывал случай, когда такая конвертация стала самой дорогой операцией вычислений.

• Минимальный размер типов с плавающей точкой для архитектуры x86 — 32 бита. Для хранения же целых чисел часто можно обойтись 16-ю битами, а в отдельных случаях восемью. Это не критично для скалярных вычислений, когда процессор в один момент времени занят выполнением одной команды. Однако в случае векторных вычислений позволяет производить в два или четыре раза больше операций за такт.

• В конце второй части было видно, что при работе AVX2-кода процессор сбавляет тактовую частоту. По моим наблюдениям это происходит только при работе с числами с плавающей точкой. Если используются целочисленные AVX2-команды, процессор продолжает работать на максимальной частоте. Конечно, это довольно специфичный пункт, поведение запросто может меняться от поколения к поколению и в зависимости от предназначения процессора. Однако вывод не меняется: числа с плавающей точкой могут работать медленнее целых чисел даже при одинаковой производительности на такт.

Фиксированная точка

Видно, что целые числа имеют потенциал более высокой производительности и можно попробовать перевести арифметику на них. Но сделать это заменив везде float на int, конечно же, не получится. При ресайзе многие расчеты ведутся в диапазоне от 0 до 1. Т.е. в представлении целыми числами это будет просто ноль.

Тут на помощь приходят числа с фиксированной точкой. Строго говоря — целые числа это тоже числа с фиксированной точкой, точка у которых зафиксирована после самого младшего двоичного разряда. Но можно умозрительно передвинуть её скажем на 8 двоичных разрядов и считать, что единица это на самом деле 1/256. Тогда 256 — это единица, 512 — двойка, а 384 — это 1,5. Что это дает? В таком виде можно записывать не только целую часть числа, но и вещественную. Довольно распространенный пример чисел с фиксированной точкой — тип данных currency, который есть в некоторых языках программирования. В нем хранится целое количество копеек или центов, а чтобы получить рубли или доллары, нужно разделить значение на сто.

Итак, еще раз: числа с фиксированной точкой — это числа, умноженные на какую-то константу для повышения точности вычислений. В отличие от чисел с плавающей точкой, эта константа не хранится в самом числе, но может быть жестко вшита в реализацию алгоритма, или быть рассчитана в процессе работы.

В целом, работа с числами с фиксированной точкой не представляет ничего сложного, но есть несколько вещей, которые нужно держать в голове.

• Диапазон значений уменьшается вместе с увеличением точности дробной части. Если подвинуть фиксированную точку на один бит влево, точность увеличится в два раза, но и диапазон значений уменьшится вдвое. Всегда нужно стараться сдвинуть точку максимально влево, но при этом избегать переполнений. Поэтому, прежде чем начинать переводить вычисления на фиксированную точку, нужно определить диапазон максимальных значений, которые будут участвовать в вычислениях. Например, если диапазон значений получился от -128 до 384, то количество бит, нужных для представления значений (включая знак), будет 10. Если используется 16-битный тип данных, то на точность останется всего 6 бит.

• Операции сложения и вычитания для чисел с фиксированной точкой работают как обычно. Умножение на целое число тоже.

• При умножении двух чисел с фиксированной точкой количество разрядов, отвечающих за точность, удваивается. Точно так же, как удваивается и количество разрядов, отвечающих за хранение целой части. То есть, если после умножения нужно получить исходную точность, результат придется сдвинуть на количество бит точности. Или можно не сдвигать, если так будет удобнее считать, но придется иметь этот факт в виду.

Подсчет точности

Прежде чем переводить код на целые числа, неплохо было бы посчитать, сколько бит можно выделить на точность. Причем такой подсчет имеет смысл для каждой операции. И начать лучше с конца:

float ss, ss0, ss1;
for (xx = 0; xx < imOut->xsize; xx++) {
    ss0 = ss1 = ss2 = 0.5;
    for (y = ymin; y < ymax; y++) {
        ss0 = ss0 + ((UINT8) imIn->image[y][xx*4+0]) * k[y-ymin];
        ss1 = ss1 + ((UINT8) imIn->image[y][xx*4+1]) * k[y-ymin];
        ss2 = ss2 + ((UINT8) imIn->image[y][xx*4+2]) * k[y-ymin];
    }
    imOut->image[yy][xx*4+0] = clip8(ss0);
    imOut->image[yy][xx*4+1] = clip8(ss1);
    imOut->image[yy][xx*4+2] = clip8(ss2);
}

Аккумуляторы ss0 — ss2 содержат сумму произведений коэффициентов на пиксели. Пиксели имеют значения в диапазоне [0, 255], а про сумму коэффициентов известно, что она равна единице. То есть и конечное значение аккумуляторов ss0 — ss2 тоже будет в диапазоне [0, 255]. Но это только конечное! А вообще, некоторые коэффициенты могут быть отрицательными, а, как следствие, сумма положительных коэффициентов может быть больше единицы (взгляните на графики фильтров из нулевой статьи). Поэтому и промежуточные значения могут незначительно выходить за пределы диапазона [0,255]. Одного бита на отрицательные числа и еще одного на возможные переполнения сверху вполне хватит в данном случае. Итого для хранения значения понадобится 10 бит [-512,511]. Так как аккумуляторы логично сделать не менее чем 32-битными, то на хранение точности аккумуляторов (назовём её PRECISION_BITS) остается 22 бита.

Осталось разобраться с умножением пикселей на коэффициенты. Я уже говорил, что при умножении числа с фиксированной точкой на целое число не нужно делать никаких дополнительных преобразований. В данном случае целое — это значения пикселей. А значит, что у коэффициентов точность может быть такой же, как у аккумуляторов — 22 бита.

Скалярные вычисления с фиксированной точкой

Это удивительно, но в коде выше нужно поменять лишь одну строку, чтобы перевести его к работе с фиксированной точкой. В самом начале аккумуляторам присваивается значение 0.5. В новой системе счисления это будет соответствовать значению 1 << (PRECISION_BITS - 1). То есть единица сдвинутая на один разряд меньше, чем точность. 0.5 новых единиц.

int ss, ss0, ss1;
for (xx = 0; xx < imOut->xsize; xx++) {
    ss0 = ss1 = ss2 = 1 << (PRECISION_BITS -1);
    for (y = ymin; y < ymax; y++) {
        ss0 = ss0 + ((UINT8) imIn->image[y][xx*4+0]) * k[y-ymin];
        ss1 = ss1 + ((UINT8) imIn->image[y][xx*4+1]) * k[y-ymin];
        ss2 = ss2 + ((UINT8) imIn->image[y][xx*4+2]) * k[y-ymin];
    }
    imOut->image[yy][xx*4+0] = clip8(ss0);
    imOut->image[yy][xx*4+1] = clip8(ss1);
    imOut->image[yy][xx*4+2] = clip8(ss2);
}

Все остальные вычисления остаются без изменения, что косвенно говорит о том, что мы на верном пути. Ведь изменение концепции не привнесло сложностей в реализацию, но все еще можно рассчитывать на выигрыш производительности.

А вот функция clip8, ограничивающая конечное значение пикселя в диапазоне [0, 255], сильно изменится. Было:

static inline UINT8 clip8(float in)
{
    int out = (int) in;
    if (out >= 255)
       return 255;
    if (out <= 0)
        return 0;
    return (UINT8) out;
}

Стало:

static inline UINT8 clip8(int in)
{
    if (in >= (1 << PRECISION_BITS << 8))
       return 255;
    if (in <= 0)
        return 0;
    return (UINT8) (in >> PRECISION_BITS);
}

Во-первых, меняется принимаемое значение — теперь это 32-разрядный int. Во-вторых, он не приводится сразу к целому типу (раньше это было в первой строке). Теперь вместо этого можно сравнить in со значением 1 << PRECISION_BITS << 8. Это значение — 256 в нашей системе счисления с фиксированно точкой, потому что сдвинуто на количество бит в дробной части и еще на 8 бит. А как известно, 1 << 8 — это как раз 256. И уже в конце, если все сравнения дали отрицательный результат, значение действительно приводится к обычному целому, без всяких точек. Приводится обычным сдвигом на количество бит точности.

Теперь к фиксированной точке нужно привести коэффициенты. Напомню, что изначально коэффициенты представляют из себя числа с плавающей точкой от -1 до 1. И сумма всех коэффициентов для расчета одного пикселя равна единице. Я уверен, что нет никакого смысла использовать целочисленную арифметику собственно для расчета коэффициентов. Во-первых, расчет коэффициентов занимает намного меньше времени, чем их использование. Во-вторых, внутри некоторых фильтров используются тригонометрические функции. Поэтому мне кажется правильным посчитать коэффициенты с плавающей точкой, а уже потом перевести их в фиксированную, домножив на (1 << PRECISION_BITS).

for (x = 0; x < xsize * kmax; x++) {
    kk[x] = (int) (prekk[x] * (1 << PRECISION_BITS));
}

Что же это дает? Вот последние результаты для скалярных вычислений, которые были получены на числах с плавающей точкой:

Scale 2560×1600 RGB image
    to 320x200 bil      0.03009 s   136.10 Mpx/s
    to 320x200 bic      0.05187 s    78.97 Mpx/s
    to 320x200 lzs      0.08113 s    50.49 Mpx/s
    to 2048x1280 bil    0.14017 s    29.22 Mpx/s
    to 2048x1280 bic    0.17750 s    23.08 Mpx/s
    to 2048x1280 lzs    0.22597 s    18.13 Mpx/s
    to 5478x3424 bil    0.58726 s     6.97 Mpx/s
    to 5478x3424 bic    0.74648 s     5.49 Mpx/s
    to 5478x3424 lzs    0.90867 s     4.51 Mpx/s

Результат для коммита 57e8925.

А вот результаты для фиксированной точки:

Scale 2560×1600 RGB image
    to 320x200 bil      0.02079 s   196.99 Mpx/s    44.7 %
    to 320x200 bic      0.03459 s   118.41 Mpx/s    50.0 %
    to 320x200 lzs      0.05649 s    72.50 Mpx/s    43.6 %
    to 2048x1280 bil    0.10483 s    39.07 Mpx/s    33.7 %
    to 2048x1280 bic    0.13362 s    30.66 Mpx/s    32.8 %
    to 2048x1280 lzs    0.17210 s    23.80 Mpx/s    31.3 %
    to 5478x3424 bil    0.46706 s     8.77 Mpx/s    25.7 %
    to 5478x3424 bic    0.59492 s     6.88 Mpx/s    25.5 %
    to 5478x3424 lzs    0.72819 s     5.62 Mpx/s    24.8 %

Результат для коммита 15d0573.

Как видите, все было не зря и прирост очень серьезный. Больше всего он заметен на сильном уменьшении, где было больше операций конвертации значений пикселей.

SIMD-вычисления с фиксированной точкой

Перевод SIMD-кода из третьей части на вычисления с фиксированной точкой можно разделить на 4 стадии:

• перевод вертикального прохода SSE4
• перевод горизонтального прохода SSE4
• перевод вертикального прохода AVX2
• перевод горизонтального прохода AVX2

Эти стадии будут довольно однообразны, поэтому есть смысл внимательно рассмотреть только одну. Вот пример вертикального прохода SSE4 на числах с плавающей точкой.

ImagingResampleVerticalConvolution8u(UINT32 *lineOut, Imaging imIn,
    int ymin, int ymax, float *k)
{
    int y, xx = 0;
    for (; xx < imIn->xsize; xx++) {
        __m128 sss = _mm_set1_ps(0.5);
        for (y = ymin; y < ymax; y++) {
            __m128i pix = _mm_cvtepu8_epi32(*(__m128i *) &imIn->image32[y][xx]);
            __m128 mmk = _mm_set1_ps(k[y - ymin]);
            __m128 mul = _mm_mul_ps(_mm_cvtepi32_ps(pix), mmk);
            sss = _mm_add_ps(sss, mul);
        }
        __m128i ssi = _mm_cvtps_epi32(sss);
        ssi = _mm_packs_epi32(ssi, ssi);
        lineOut[xx] = _mm_cvtsi128_si32(_mm_packus_epi16(ssi, ssi));
    }
}

Тип данных __m128 хранит 4 числа с плавающей точкой. Он больше не понадобится, его следует заменить на __m128i. Аналогом функции _mm_set1_ps будет _mm_set1_epi32. Функции конвертации _mm_cvtepi32_ps и _mm_cvtps_epi32 больше не понадобятся, вместо этого результат в конце нужно будет сдвинуть на PRECISION_BITS вправо. Затруднения могут возникнуть только с функцией _mm_mul_ps, потому что прямого аналога для нее нет, но если поискать, то находится _mm_mullo_epi32. Дело в том, что умножение двух 32-разрядных чисел дает 64-разрядное число. Lo означает, что вернутся младшие 32 бита результата, что как раз нужно. Полностью весь код будет выглядеть так:

ImagingResampleVerticalConvolution8u(UINT32 *lineOut, Imaging imIn,
    int ymin, int ymax, int *intk)
{
    int y, xx = 0;
    for (; xx < imIn->xsize; xx++) {
        __m128i sss = _mm_set1_epi32(1 << (PRECISION_BITS -1));
        for (y = ymin; y < ymax; y++) {
            __m128i pix = _mm_cvtepu8_epi32(*(__m128i *) &imIn->image32[y][xx]);
            __m128i mmk = _mm_set1_epi32(intk[y - ymin]);
            __m128i mul = _mm_mullo_epi32(pix, mmk);
            sss = _mm_add_epi32(sss, mul);
        }
        sss = _mm_srai_epi32(sss, PRECISION_BITS);
        sss = _mm_packs_epi32(sss, sss);
        lineOut[xx] = _mm_cvtsi128_si32(_mm_packus_epi16(sss, sss));
    }
}

Теперь можно сравнить результаты, полученные для SSE4-версии на числах с плавающей точкой:

Scale 2560×1600 RGB image
    to 320x200 bil      0.01151 s   355.87 Mpx/s
    to 320x200 bic      0.02005 s   204.27 Mpx/s
    to 320x200 lzs      0.03421 s   119.73 Mpx/s
    to 2048x1280 bil    0.04450 s    92.05 Mpx/s
    to 2048x1280 bic    0.05951 s    68.83 Mpx/s
    to 2048x1280 lzs    0.07804 s    52.49 Mpx/s
    to 5478x3424 bil    0.18615 s    22.00 Mpx/s
    to 5478x3424 bic    0.24039 s    17.04 Mpx/s
    to 5478x3424 lzs    0.30674 s    13.35 Mpx/s

Результат для коммита 8d0412b.

С результатами, полученными для SS4 на числах с фиксированной точкой:

Scale 2560×1600 RGB image
    to 320x200 bil      0.01253 s   326.82 Mpx/s    -8.1 %
    to 320x200 bic      0.02239 s   182.94 Mpx/s   -10.5 %
    to 320x200 lzs      0.03663 s   111.83 Mpx/s    -6.6 %
    to 2048x1280 bil    0.04712 s    86.92 Mpx/s    -5.6 %
    to 2048x1280 bic    0.06731 s    60.86 Mpx/s   -11.6 %
    to 2048x1280 lzs    0.08176 s    50.10 Mpx/s    -4.5 %
    to 5478x3424 bil    0.19010 s    21.55 Mpx/s    -2.1 %
    to 5478x3424 bic    0.25013 s    16.38 Mpx/s    -3.9 %
    to 5478x3424 lzs    0.31413 s    13.04 Mpx/s    -2.4 %

Результат для коммита 7d8df66.

И тут меня ждал сюрприз. Я долго пытался понять, что пошло не так. В какой-то момент я пошел смотреть тайминги каждой инструкции, которая использовалась в цикле и разгадка была именно тут.

Сейчас в справочнике Intel Intrinsics Guide этого не видно, потому что он постоянно обновляется и время от времени из него удаляют данные для старых процессоров. Но когда я разбирался с этим вопросом, у операции _mm_mullo_epi32 была такая таблица таймингов:

Architecture  Latency   Throughput
Broadwell     10        2
Haswell       10        2
Ivy Bridge    5         1

А теперь сравните с таймингами аналогичной команды _mm_mul_ps для чисел с плавающей точкой:

Architecture  Latency   Throughput
Broadwell     3         0.5
Haswell       5         0.5
Ivy Bridge    5         1

Тут видно, что, начиная с архитектуры Haswell, Intel забила на векторное умножение целых 32-битных чисел. Причем именно целых и именно 32-битных, потому что все остальные варианты умножений продолжают становиться быстрее от архитектуры к архитектуре.

Что интересно, для AVX2-версии кода такого не наблюдается и негативный эффект от увеличения задержек не преобладает над положительным эффектом от перехода на вычисления с фиксированной точкой. И прирост производительности для чисел с фиксированной точкой составляет ≈10%. Тому есть две причины:

• Как я говорил в самом начале, процессор не сбавляет частоту, когда выполняет целочисленные AVX2-инструкции, в отличие от AVX2-инструкций с плавающей точкой.
• AVX2-версия за раз обрабатывает в 2 раза больше данных, а значит и инструкция умножения выполняется в 2 раза реже для того же объема данных. А значит и негативный эффект от больших задержек в 2 раза менее заметен.

Поиски Святого Грааля

Я готовил целочисленные вычисления для Pillow версии 3.3. И я старался выпускать версии Pillow и Pillow-SIMD более-менее синхронно и с одинаковыми улучшениями. И было очень обидно, что переход на целые числа давал ощутимый прирост в Pillow, но давал незначительный или не давал никакого в Pillow-SIMD. Тогда, в релизе, я смог немного компенсировать отставание с помощью разворачивания циклов. Это позволило улучшить конвейер команд и немного устранило эффект от медленного умножения. Но про это я бы хотел рассказать в последней статье этой серии.

Если посмотреть на то, как изменялась производительность обычной версии Pillow, то будет видно, что в Pillow 3.3 был неплохой прирост за счет целочисленных вычислений. А в Pillow 3.4 все осталось практически на том же уровне.

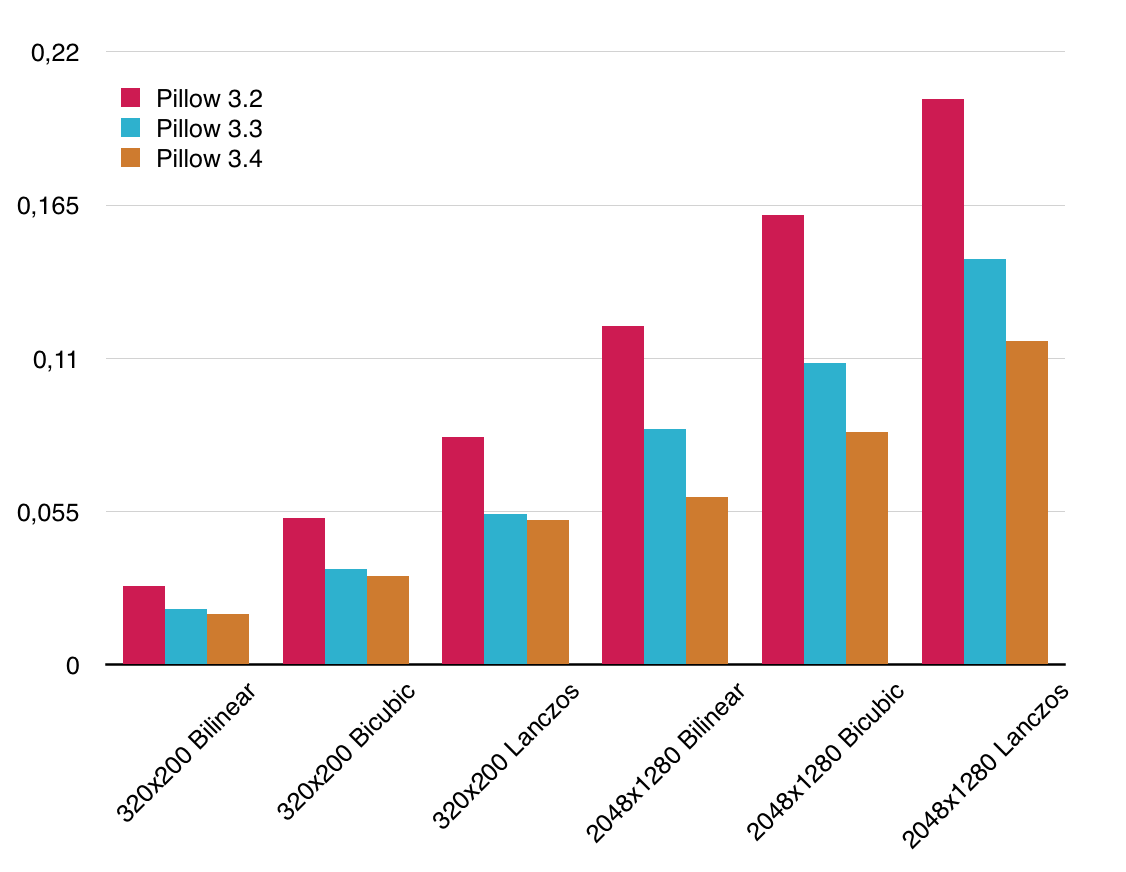
Тогда как для Pillow-SIMD ситуация обратная: версия 3.3 оказалась едва ли не медленнее предыдущей. Зато в 3.4 был существенный скачек, который и позволяет мне сейчас говорить, что Pillow-SIMD на текущий момент самая быстрая реализация ресайза на CPU.

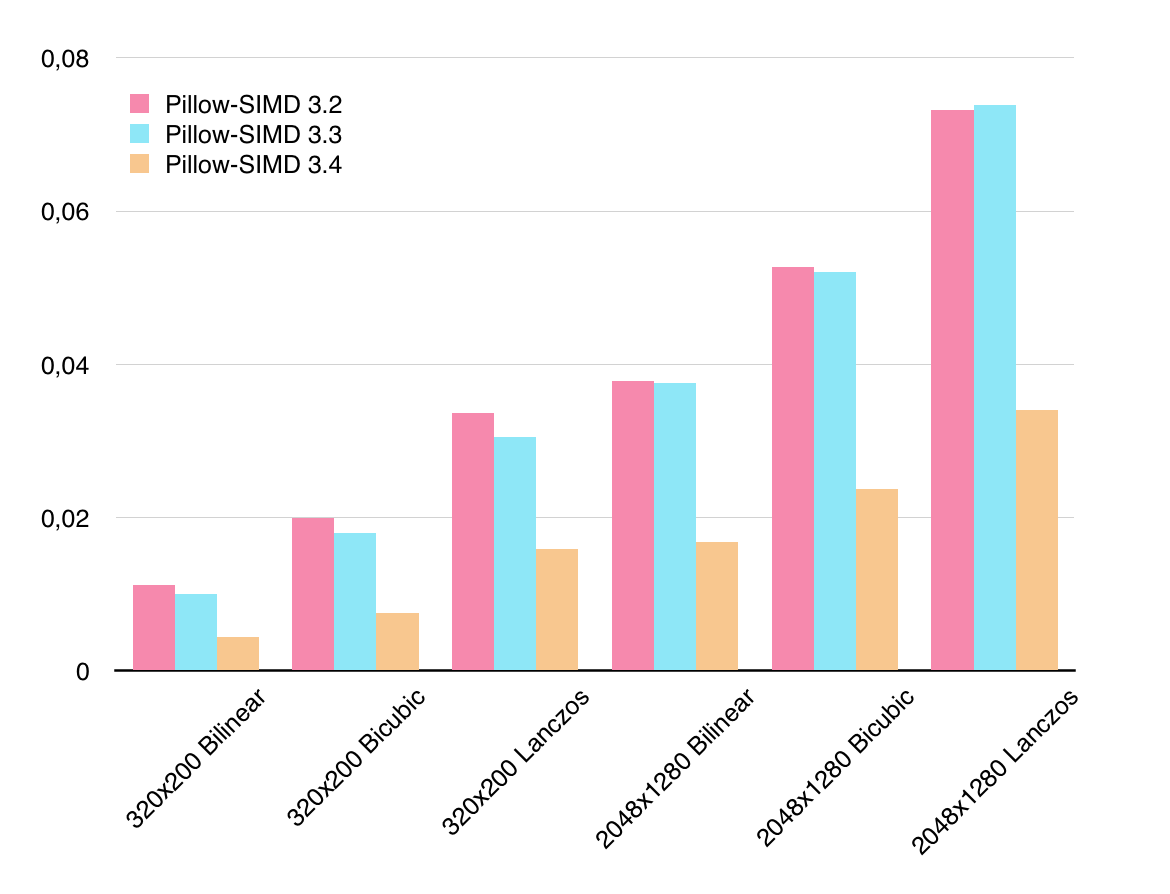
Чтобы достичь таких улучшений в Pillow-SIMD 3.4, нужно было избавиться от векторного 32-битного умножения целых чисел. Но как? Перевести все вычисления на 16 бит? Несложно посчитать, что в этом случае на коэффициенты (PRECISION_BITS) оставалось бы 16−8−2 = 6 бит, то есть всего 64 значения. На практике намного меньше, потому что сумма всех коэффициентов должна быть равна единице (то есть 64). А количество коэффициентов зависит от размера окна фильтра и масштаба уменьшения (подробности в части 0). При уменьшении изображения в 10 раз с фильтром Ланцоша, самих коэффициентов будет шестьдесят. Вычисления в 16 битах явно были недостаточно точны, нужно было придумать что-то еще.

Мне не давала покоя мысль: почему-то же Intel решила таким странным образом зарубить умножение. И другие разработчики не сокрушаются по этому поводу в интернетах, но продолжают успешно решать свои задачи. Может быть 32-битное умножение правда не нужно для работы с графикой, просто я не вижу, как обойтись без него.

Я присматривался к _mm_mullo_epi16. Можно было попробовать хитро подбирать разрядность коэффициентов, чтобы результат свертки был 32-битным, но результат умножения значения пикселя на коэффициент оставался в пределах 16 бит. Тогда на точность самого коэффициента оставалось бы 7 бит (один бит пошел на знак). Это было значительно лучше, чем 6 бит на сумму всех коэффициентов. Я уже собирался это реализовывать, когда случайно наткнулся на другое решение.

А что если бы для сверток была специальная инструкция?

Представьте, вы решаете задачу, рассматриваете под разными углами инструменты, которые у вас есть, а потом случайно натыкаетесь на такой, который специально был придуман для этой задачи.

В чем сложность умножения? На хранение результата умножения нужно в два раза больше бит, чем на операнды. Поэтому приходится выбирать: верхнюю или нижнюю часть результата нужно получить. От этого страдает точность, а от операндов используется лишь часть значащих битов. Что если бы можно было получить весь результат умножения? Тогда бы под него понадобилось в два раза больше бит, то есть, например, два регистра с результатом. Но что если после умножения сложить эти два регистра? Все равно же нужно будет сложить результат умножения, в этом и заключается смысл свертки. Тогда бы получилась инструкция, которая принимает X пар операндов для умножения, умножает их, получает X произведений, потом складывает соседние и на выходе отдает X/2 сумм произведений. И, как ни странно, такая инструкция нашлась аж в SSE2! Называется она _mm_madd_epi16. И задержки у нее в два раза ниже, чем у _mm_mullo_epi32, а операций она выполняет в 3 раза больше.

Еще раз: на входе два регистра, в каждом по восемь 16-битных целых чисел со знаком. Эти числа попарно перемножаются, где-то в уме сохраняется восемь 32-битных результатов умножения. Соседние результаты умножений складываются и получается четыре 32-битных числа со знаком. Восемь умножений и четыре сложения одной быстрой инструкцией вместо четырех умножений медленной. Практически без потери точности.

Единственная проблема только в том, что складываются соседние результаты умножений, а для пикселей это будут соседние каналы. Если применить команду в лоб, красный канал первого пикселя сложится с зеленым первого пикселя, а синий первого пикселя сложится с альфа-каналом. То же самое для второго пикселя. А для сверток нужно складывать красный канал первого пикселя с красным каналом второго и так далее. То есть значения нужно немного перемешать перед применением этой инструкции.

Переход на 16-битные коэффициенты

Просто заменить тип int на INT16, к сожалению, недостаточно: коэффициенты могут выходить за пределы этого типа. Вначале я говорил, что экспонента (точность числа или положение виртуальной фиксированной точки, как хотите) может быть задана как в самом алгоритме, так и вычисляться в процессе работы. И тут как раз тот случай, когда в зависимости от разных входных данных нужно будет выбирать разные экспоненты. И для этого расчета понадобится значение максимального из коэффициентов.

#define MAX_COEFS_PRECISION (16 - 1)
#define PRECISION_BITS (32 - 8 - 2)

coefs_precision = 0;
while (
    maxkk < (1 << (MAX_COEFS_PRECISION-1)) &&
    (coefs_precision < PRECISION_BITS)
) {
    maxkk *= 2;
    coefs_precision += 1;
};

То есть нужно следить, чтобы, с одной стороны, значение максимального коэффициента не выходило за 16 бит (потому что он будет представлен в 16-битном виде), а с другой, чтобы значение всей свертки не выходило за 32 бита (это условие выполняется пока coefs_precision < PRECISION_BITS).

Мне кажется, я и так достаточно утомил кодом, поэтому не буду разбирать, что именно нужно изменить и как перемешать пиксели, чтобы можно было применить инструкцию _mm_madd_epi16. Интересующиеся как всегда могут посмотреть изменения в коммитах на гитхабе и задать вопросы в комментариях. Приведу сразу результаты SSE4-версии на 16-битных коэффициентах относительно SSE4-версии на числах с плавающей точкой:

Scale 2560×1600 RGB image
    to 320x200 bil      0,00844 s   485.20 Mpx/s   36,4 %
    to 320x200 bic      0,01289 s   317.79 Mpx/s   55,5 %
    to 320x200 lzs      0,01903 s   215.24 Mpx/s   79,8 %
    to 2048x1280 bil    0,04481 s    91.41 Mpx/s   -0,7 %
    to 2048x1280 bic    0,05419 s    75.59 Mpx/s    9,8 %
    to 2048x1280 lzs    0,06930 s    59.11 Mpx/s   12,6 %
    to 5478x3424 bil    0,19939 s    20.54 Mpx/s   -6,6 %
    to 5478x3424 bic    0,24559 s    16.68 Mpx/s   -2,1 %
    to 5478x3424 lzs    0,29152 s    14.05 Mpx/s    5,2 %

Результат для коммита 9b9a91f.

И результаты AVX2-версии на 16-битных коэффициентах относительно AVX2-версии на числах с плавающей точкой:

Scale 2560×1600 RGB image
    to 320x200 bil      0.00682 s   600.15 Mpx/s   34.6 %
    to 320x200 bic      0.00990 s   413.86 Mpx/s   50.5 %
    to 320x200 lzs      0.01424 s   287.54 Mpx/s   60.6 %
    to 2048x1280 bil    0.03889 s   105.31 Mpx/s    7.6 %
    to 2048x1280 bic    0.04519 s    90.64 Mpx/s   11.3 %
    to 2048x1280 lzs    0.05226 s    78.38 Mpx/s   18.2 %
    to 5478x3424 bil    0.15195 s    26.96 Mpx/s    6.7 %
    to 5478x3424 bic    0.16977 s    24.13 Mpx/s   17.8 %
    to 5478x3424 lzs    0.20229 s    20.25 Mpx/s   15.6 %

Результат для коммита 3ad4718.

Итого

Итого, переход на целочисленные вычисления дал выигрыш как для скалярного кода, так и для SIMD. Есть небольшая регрессия производительности в SSE4-версии при увеличении изображений с использованием некоторых фильтров. Но дело в том, что представленный тут код довольно сильно отличается от того, что входил в версии Pillow-SIMD 3.3 или 3.4 — это некий винегрет, промежуточное звено, где применены одни оптимизации, но не применены другие. В реальных версиях деградации производительности не было.

Если оглянуться назад и вспомнить самую первую версию, окажется, что текущий код в 10-12 раз быстрее на том же железе. То, что занимало 2 секунды, теперь можно выполнять 5 раз в секунду! Но если посмотреть официальные бенчмарки, то видно, что реальная производительность Pillow-SIMD 3.4 с AVX2 все еще в 2 раза выше, чем получилась к концу этой статьи. А значит, есть повод и материал для следующей части.

Автор: homm

Источник