Начать стоит от печки, то есть с постановки задачи. Откуда берется сама задача word embedding?
Лирическое отступление: К сожалению, русскоязычное сообщество еще не выработало единого термина для этого понятия, поэтому мы будем использовать англоязычный.
Сам по себе embedding — это сопоставление произвольной сущности (например, узла в графе или кусочка картинки) некоторому вектору.
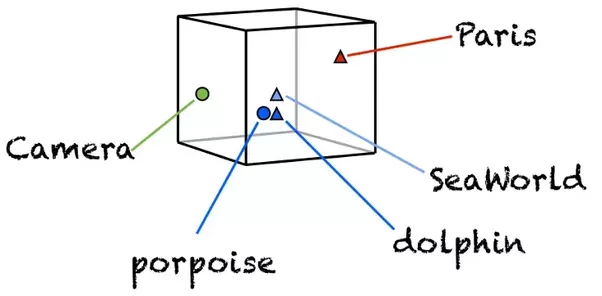
Сегодня мы говорим про слова и стоит обсудить, как делать такое сопоставление вектора слову.
Вернемся к предмету: вот у нас есть слова и есть компьютер, который должен с этими словами как-то работать. Вопрос — как компьютер будет работать со словами? Ведь компьютер не умеет читать, и вообще устроен сильно иначе, чем человек. Самая первая идея, приходящая в голову — просто закодировать слова цифрами по порядку следования в словаре. Идея очень продуктивна в своей простоте — натуральный ряд бесконечен и можно перенумеровать все слова, не опасаясь проблем. (На секунду забудем про ограничения типов, тем более, в 64-битное слово можно запихнуть числа от 0 до 2^64 — 1, что существенно больше количества всех слов всех известных языков.)
Но у этой идеи есть и существенный недостаток: слова в словаре следуют в алфавитном порядке, и при добавлении слова нужно перенумеровывать заново большую часть слов. Но даже это не является настолько важным, а важно то, буквенное написание слова никак не связано с его смыслом (эту гипотезу еще в конце XIX века высказал известный лингвист Фердинанд де Соссюр). В самом деле слова “петух”, “курица” и “цыпленок” имеют очень мало общего между собой и стоят в словаре далеко друг от друга, хотя очевидно обозначают самца, самку и детеныша одного вида птицы. То есть мы можем выделить два вида близости слов: лексический и семантический. Как мы видим на примере с курицей, эти близости не обязательно совпадают. Можно для наглядности привести обратный пример лексически близких, но семантически далеких слов — "зола" и "золото". (Если вы никогда не задумывались, то имя Золушка происходит именно от первого.)
Чтобы получить возможность представить семантическую близость, было предложено использовать embedding, то есть сопоставить слову некий вектор, отображающий его значение в “пространстве смыслов”.
Какой самый простой способ получить вектор из слова? Кажется, что естественно будет взять вектор длины нашего словаря и поставить только одну единицу в позиции, соответствующей номеру слова в словаре. Этот подход называется one-hot encoding (OHE). OHE все еще не обладает свойствами семантической близости:

Значит нам нужно найти другой способ преобразования слов в вектора, но OHE нам еще пригодится.
Отойдем немного назад — значение одного слова нам может быть и не так важно, т.к. речь (и устная, и письменная) состоит из наборов слов, которые мы называем текстами. Так что если мы захотим как-то представить тексты, то мы возьмем OHE-вектор каждого слова в тексте и сложим вместе. Т.е. на выходе получим просто подсчет количества различных слов в тексте в одном векторе. Такой подход называется “мешок слов” (bag of words, BoW), потому что мы теряем всю информацию о взаимном расположении слов внутри текста.
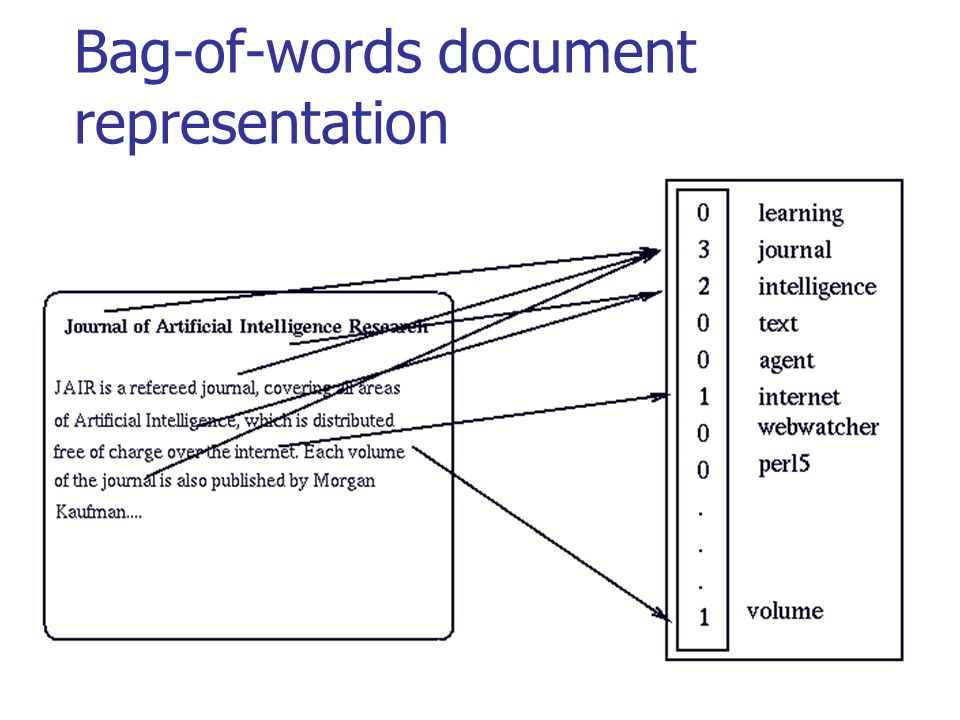
Но несмотря на потерю этой информации так тексты уже можно сравнивать. Например, с помощью косинусной меры.
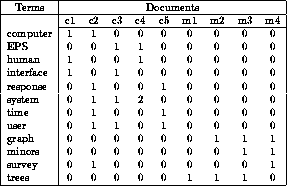
Мы можем пойти дальше и представить наш корпус (набор текстов) в виде матрицы “слово-документ” (term-document). Стоит отметить, что в области информационного поиска (information retrieval) эта матрица носит название "обратного индекса" (inverted index), в том смысле, что обычный/прямой индекс выглядит как "документ-слово" и очень неудобен для быстрого поиска. Но это опять же выходит за рамки нашей статьи.
Эта матрица приводит нас к тематическим моделям, где матрицу “слово-документ” пытаются представить в виде произведения двух матриц “слово-тема” и “тема-документ”. В самом простом случае мы возьмем матрицу и с помощью SVD-разложения получим представление слов через темы и документов через темы:
Здесь $inline$t_i$inline$ — слова, $inline$d_i$inline$ — документы. Но это уже будет предметом другой статьи, а сейчас мы вернемся к нашей главной теме — векторному представлению слов.
Пусть у нас есть такой корпус:
s = ['Mars has an athmosphere', "Saturn 's moon Titan has its own athmosphere",
'Mars has two moons', 'Saturn has many moons', 'Io has cryo-vulcanoes']
С помощью SVD-преобразования, выделим только первые две компоненты, и нарисуем:
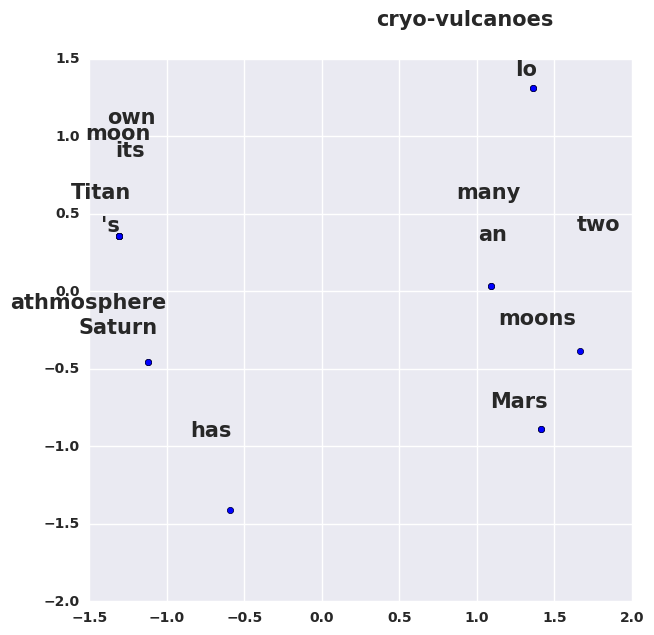
Что интересного на этой картинке? То, что Титан и Ио — далеко друг от друга, хотя они оба являются спутниками Сатурна, но в нашем корпусе про это ничего нет. Слова "атмосфера" и "Сатурн" очень близко друг другу, хотя не являются синонимами. В то же время "два" и "много" стоят рядом, что логично. Но общий смысл этого примера в том, что результаты, которые вы получите очень сильно зависят от корпуса, с которым вы работаете. Весь код для получения картинки выше можно посмотреть здесь.
Логика повествования выводит на следующую модификацию матрицы term-document — формулу TF-IDF. Эта аббревиатура означает "term frequency — inverse document frequency".
$$display$$TF-IDF(w, d, C)=frac{count(w, d)}{count(d)}*log(frac{sum_{d' in C}{mathbb{1}(w,d')}}{|C|})$$display$$
Давайте попробуем разобраться, что это такое. Итак, TF — это частота слова $inline$w$inline$ в тексте $inline$d$inline$, здесь нет ничего сложного. А вот IDF — существенно более интересная вещь: это логарифм обратной частоты распространенности слова $inline$w$inline$ в корпусе $inline$С$inline$. Распространенностью называется отношение числа текстов, в которых встретилось искомое слово, к общему числу текстов в корпусе. С помощью TF-IDF тексты также можно сравнивать, и делать это можно с меньшей опаской, чем при использовании обычных частот.
Новая эпоха
Описанные выше подходы были (и остаются) хороши для времен (или областей), где количество текстов мало и словарь ограничен, хотя, как мы видели, там тоже есть свои сложности. Но с приходом в нашу жизнь интернета все стало одновременно и сложнее и проще: в доступе появилось великое множество текстов, и эти тексты с изменяющимся и расширяющимся словарем. С этим надо было что-то делать, а ранее известные модели не могли справиться с таким объемом текстов. Количество слов в английском языке очень грубо составляет миллион — матрица совместных встречаемостей только пар слов будет 10^6 x 10^6. Такая матрица даже сейчас не очень лезет в память компьютеров, а, скажем, 10 лет назад про такое можно было не мечтать. Конечно, были придуманы множество способов, упрощающих или распараллеливающих обработку таких матриц, но все это были паллиативные методы.
И тогда, как это часто бывает, был предложен выход по принципу “тот, кто нам мешает, тот нам поможет!” А именно, в 2013 году тогда мало кому известный чешский аспирант Томаш Миколов предложил свой подход к word embedding, который он назвал word2vec. Его подход основан на другой важной гипотезе, которую в науке принято называть гипотезой локальности — “слова, которые встречаются в одинаковых окружениях, имеют близкие значения”. Близость в данном случае понимается очень широко, как то, что рядом могут стоять только сочетающиеся слова. Например, для нас привычно словосочетание "заводной будильник". А сказать “заводной апельсин” мы не можем* — эти слова не сочетаются.
Основываясь на этой гипотезе Томаш Миколов предложил новый подход, который не страдал от больших объемов информации, а наоборот выигрывал [1].

Модель, предложенная Миколовым очень проста (и потому так хороша) — мы будем предсказывать вероятность слова по его окружению (контексту). То есть мы будем учить такие вектора слов, чтобы вероятность, присваиваемая моделью слову была близка к вероятности встретить это слово в этом окружении в реальном тексте.
$$display$$P(w_o| w_c)=frac{e^{s(w_o, w_c)}}{sum_{w_i in V} e^{s(w_i, w_c)}}$$display$$
Здесь $inline$w_o$inline$ — вектор целевого слова, $inline$w_c$inline$ — это некоторый вектор контекста, вычисленный (например, путем усреднения) из векторов окружающих нужное слово других слов. А $inline$s(w_1, w_2)$inline$ — это функция, которая двум векторам сопоставляет одно число. Например, это может быть упоминавшееся выше косинусное расстояние.
Приведенная формула называется softmax, то есть “мягкий максимум”, мягкий — в смысле дифференцируемый. Это нужно для того, чтобы наша модель могла обучиться с помощью backpropagation, то есть процесса обратного распространения ошибки.
Процесс тренировки устроен следующим образом: мы берем последовательно (2k+1) слов, слово в центре является тем словом, которое должно быть предсказано. А окружающие слова являются контекстом длины по k с каждой стороны. Каждому слову в нашей модели сопоставлен уникальный вектор, который мы меняем в процессе обучения нашей модели.
В целом, этот подход называется CBOW — continuous bag of words, continuous потому, что мы скармливаем нашей модели последовательно наборы слов из текста, a BoW потому что порядок слов в контексте не важен.
Также Миколовым сразу был предложен другой подход — прямо противоположный CBOW, который он назвал skip-gram, то есть “словосочетание с пропуском”. Мы пытаемся из данного нам слова угадать его контекст (точнее вектор контекста). В остальном модель не претерпевает изменений.
Что стоит отметить: хотя в модель не заложено явно никакой семантики, а только статистические свойства корпусов текстов, оказывается, что натренированная модель word2vec может улавливать некоторые семантические свойства слов. Классический пример из работы автора:
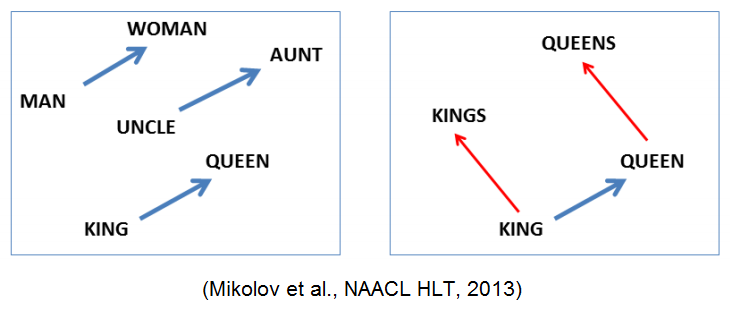
Слово "мужчина" относится к слову "женщина" так же, как слово "дядя" к слову "тётя", что для нас совершенно естественно и понятно, но в других моделям добиться такого же соотношения векторов можно только с помощью специальных ухищрений. Здесь же — это происходит естественно из самого корпуса текстов. Кстати, помимо семантических связей, улавливаются и синтаксические, справа показано соотношение единственного и множественного числа.
Более сложные вещи
На самом деле, за прошедшее время были предложены улучшения ставшей уже также классической модели Word2Vec. Два самых распространенных будут описаны ниже. Но этот раздел может быть пропущен без ущерба для понимания статьи в целом, если покажется слишком сложным.
Negative Sampling
В стандартной модели CBoW, рассмотренной выше, мы предсказываем вероятности слов и оптимизируем их. Функцией для оптимизации (минимизации в нашем случае) служит дивергенция Кульбака-Лейблера:
$$display$$KL(p||q) = int{p(x) logfrac{p(x)}{q(x)}} dx$$display$$
Здесь $inline$p(x)$inline$ — распределение вероятностей слов, которое мы берем из корпуса, $inline$q(x)$inline$ — распределение, которое порождает наша модель. Дивергенция — это буквально "расхождение", насколько одно распределение не похоже на другое. Т.к. наши распределения на словах, т.е. являются дискретными, мы можем заменить в этой формуле интеграл на сумму:
$$display$$KL(p||q) = sum_{x in V}{p(x) logfrac{p(x)}{q(x)}}$$display$$
Оказалось так, что оптимизировать эту формулу достаточно сложно. Прежде всего из-за того, что $inline$q(x)$inline$ рассчитывается с помощью softmax по всему словарю. (Как мы помним, в английском сейчас порядка миллиона слов.) Здесь стоит отметить, что многие слова вместе не встречаются, как мы уже отмечали выше, поэтому большая часть вычислений в softmax является избыточной. Был предложен элегантный обходной путь, который получил название Negative Sampling. Суть этого подхода заключается в том, что мы максимизируем вероятность встречи для нужного слова в типичном контексте (том, который часто встречается в нашем корпусе) и одновременно минимизируем вероятность встречи в нетипичном контексте (том, который редко или вообще не встречается). Формулой мысль выше записывается так:
$$display$$NegS(w_o) = sum_{i=1, x_i thicksim D}^{i=k}{-log(1 + e^{s(x_i, w_o)})} + sum_{j=1, x_j thicksim D'}^{j=l}{-log(1 + e^{-s(x_j, w_o)})}$$display$$
Здесь $inline$s(x,w)$inline$ — точно такой же, что и в оригинальной формуле, а вот остальное несколько отличается. Прежде всего стоит обратить внимание на то, что формуле теперь состоит из двух частей: позитивной ($inline$s(x,w)$inline$) и негативной ($inline$-s(x,w)$inline$). Позитивная часть отвечает за типичные контексты, и $inline$D$inline$ здесь — это распределение совместной встречаемости слова $inline$w$inline$ и остальных слов корпуса. Негативная часть — это, пожалуй, самое интересное — это набор слов, которые с нашим целевым словом встречаются редко. Этот набор порождается из распределения $inline$D'$inline$, которое на практике берется как равномерное по всем словам словаря корпуса. Было показано, что такая функция приводит при своей оптимизации к результату, аналогичному стандартному softmax [2].
Hierarchical SoftMax
Также люди зашли и с другой стороны — можно не менять исходную формулу, а попробовать посчитать сам softmax более эффективно. Например, используя бинарное дерево [3]. По всем словам в словаре строится дерево Хаффмана. В полученном дереве $inline$V$inline$ слов располагаются на листьях дерева.
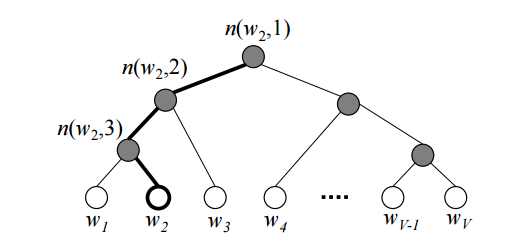
На рисунке изображен пример такого бинарного дерева. Жирным выделен путь от корня до слова $inline$w_2$inline$. Длину пути обозначим $inline$L(w)$inline$, а $inline$j$inline$-ую вершину на пути к слову $inline$w$inline$ обозначим через $inline$n(w,j)$inline$. Можно доказать, что внутренних вершин (не листьев) $inline$V − 1$inline$.
С помощью иерархического softmax вектора $inline$v_{n(w,j)}$inline$ предсказывается для $inline$V-1$inline$ внутренних вершин. А вероятность того, что слово $inline$w$inline$ будет выходным словом (в зависимости от того, что мы предсказываем: слово из контекста или заданное слово по контексту) вычисляется по формуле:
$inline$p(w=w_o)=prodlimits_{j=1}^{L(w)-1}sigma([n(w,j+1)=lch(n(w,j))] v_{n(w,j)}^T u)$inline$
где $inline$sigma(x)$inline$ — функция softmax; $inline$[true]=1,[false]=-1$inline$; $inline$lch(n)$inline$ — левый сын вершины $inline$n$inline$; $inline$u=v_{w_I}$inline$, если используется метод skip-gram, $inline$u=frac{1}{h} sumlimits_{k=1}^{h} v_{w_{I,k}}$inline$, то есть, усредненный вектор контекста, если используется CBOW.
Формулу можно интуитивно понять, представив, что на каждом шаге мы можем пойти налево или направо с вероятностями:
$inline$p(n,left)=sigma(v_n^T u)$inline$
$inline$p(n,right)=1-p(n,left)=1-sigma(v_n^T u)=sigma(-v_n^T u)$inline$
Затем на каждом шаге вероятности перемножаются ($inline$L(w)-1$inline$ шагов) и получается искомая формула.
При использовании простого softmax для подсчета вероятности слова, приходилось вычислять нормирующую сумму по всем словам из словаря, требовалось $inline$O(V)$inline$ операций. Теперь же вероятность слова можно вычислить при помощи последовательных вычислений, которые требуют $inline$O(log(V))$inline$.
Другие модели
Помимо word2vec были, само собой, предложены и другие модели word embedding. Стоит отметить модель, предложенную лабораторией компьютерной лингвистики Стенфордского университета, под названием Global Vectors (GloVe), сочетающую в себе черты SVM разложения и word2vec [4].
Также надо упомянуть о том, что т.к. изначально все описанные модели были предложены для английского языка, то там не так остро стоит проблема словоизменения, характерная для синтетических языков (это — лингвистический термин), вроде русского. Везде выше по тексту неявно предполагалось, что мы либо считаем разные формы одного слова разными словами — и тогда надеяться, что нашего корпуса будет достаточно модели, чтобы выучить их синтаксическую близость, либо используем механизмы стеммирования или лемматизации. Стеммирование — это обрезание окончания слова, оставление только основы (например, “красного яблока” превратится в “красн яблок”). А лемматизация — замена слова его начальной формой (например, “мы бежим” превратится в “я бежать”). Но мы можем и не терять эту информацию, а использовать ее — закодировав OHE в новый вектор, и сконкатинировать его с вектором для основы или леммы.
Еще стоит сказать, что то, с чем мы начинали — буквенное представление слова — тоже не кануло в Лету: предложены модели по использованию буквенного представления слова для word embedding [5].
Практическое применение
Мы поговорили о теории, пришло время посмотреть, к чему все вышеописанное применимо на практике. Ведь любая самая красивая теория без практического применения — не более чем игра ума. Рассмотрим применение Word2Vec в двух задачах:
1) Задача классификации, необходимо по последовательности посещенных сайтов определять пользователя;
2) Задача регрессии, необходимо по тексту статьи определить ее рейтинг на Хабрахабре.
Классификация
# загрузим библиотеки и установим опции
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
#%matplotlib inline
import numpy as np
import pandas as pd
from sklearn.metrics import roc_auc_scoreCкачать данные для первой задачи можно со страницы соревнования "Catch Me If You Can"
# загрузим обучающую и тестовую выборки
train_df = pd.read_csv('data/train_sessions.csv')#,index_col='session_id')
test_df = pd.read_csv('data/test_sessions.csv')#, index_col='session_id')
# приведем колонки time1, ..., time10 к временному формату
times = ['time%s' % i for i in range(1, 11)]
train_df[times] = train_df[times].apply(pd.to_datetime)
test_df[times] = test_df[times].apply(pd.to_datetime)
# отсортируем данные по времени
train_df = train_df.sort_values(by='time1')
# посмотрим на заголовок обучающей выборки
train_df.head()
sites = ['site%s' % i for i in range(1, 11)]
#заменим nan на 0
train_df[sites] = train_df[sites].fillna(0).astype('int').astype('str')
test_df[sites] = test_df[sites].fillna(0).astype('int').astype('str')
#создадим тексты необходимые для обучения word2vec
train_df['list'] = train_df['site1']
test_df['list'] = test_df['site1']
for s in sites[1:]:
train_df['list'] = train_df['list']+","+train_df[s]
test_df['list'] = test_df['list']+","+test_df[s]
train_df['list_w'] = train_df['list'].apply(lambda x: x.split(','))
test_df['list_w'] = test_df['list'].apply(lambda x: x.split(','))#В нашем случае предложение это набор сайтов, которые посещал пользователь
#нам необязательно переводить цифры в названия сайтов, т.к. алгоритм будем выявлять взаимосвязь их друг с другом.
train_df['list_w'][10]['229', '1500', '33', '1500', '391', '35', '29', '2276', '40305', '23']# подключим word2vec
from gensim.models import word2vec#объединим обучающую и тестовую выборки и обучим нашу модель на всех данных
#с размером окна в 6=3*2 (длина предложения 10 слов) и итоговыми векторами размерности 300, параметр workers отвечает за количество ядер
test_df['target'] = -1
data = pd.concat([train_df,test_df], axis=0)
model = word2vec.Word2Vec(data['list_w'], size=300, window=3, workers=4)
#создадим словарь со словами и соответсвующими им векторами
w2v = dict(zip(model.wv.index2word, model.wv.syn0))Т.к. сейчас мы каждому слову сопоставили вектор, то нужно решить, что сопоставить целому предложению из слов.
Один из возможных вариантов это просто усреднить все слова в предложении и получить некоторый смысл всего предложения (если слова нет в тексте, то берем нулевой вектор).
class mean_vectorizer(object):
def __init__(self, word2vec):
self.word2vec = word2vec
self.dim = len(next(iter(w2v.values())))
def fit(self, X):
return self
def transform(self, X):
return np.array([
np.mean([self.word2vec[w] for w in words if w in self.word2vec]
or [np.zeros(self.dim)], axis=0)
for words in X
])data_mean=mean_vectorizer(w2v).fit(train_df['list_w']).transform(train_df['list_w'])
data_mean.shape(253561, 300)Т.к. мы получили distributed representation, то никакая число по отдельноти ничего не значит, а значит лучше всего покажут себя линейные алгоритмы. Попробуем нейронные сети, LogisticRegression и проверим нелинейный метод XGBoost.
# Воспользуемся валидацией
def split(train,y,ratio):
idx = round(train.shape[0] * ratio)
return train[:idx, :], train[idx:, :], y[:idx], y[idx:]
y = train_df['target']
Xtr, Xval, ytr, yval = split(data_mean, y,0.8)
Xtr.shape,Xval.shape,ytr.mean(),yval.mean()((202849, 300), (50712, 300), 0.009726446765820882, 0.006389020350212968)# подключим библиотеки keras
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Activation, Input
from keras.preprocessing.text import Tokenizer
from keras import regularizers# опишем нейронную сеть
model = Sequential()
model.add(Dense(128, input_dim=(Xtr.shape[1])))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(1))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['binary_accuracy'])history = model.fit(Xtr, ytr,
](https://habrastorage.org/web/c92/477/565/c924775650e44c469e20c3eaa9705bfa.png) batch_size=128,
epochs=10,
validation_data=(Xval, yval),
class_weight='auto',
verbose=0)classes = model.predict(Xval, batch_size=128)
roc_auc_score(yval, classes)0.91892341356995644Получили неплохой результат. Значит Word2Vec смог выявить зависимости между сессиями.
Посмотрим, что произойдет с алгоритмом XGBoost.
import xgboost as xgbdtr = xgb.DMatrix(Xtr, label= ytr,missing = np.nan)
dval = xgb.DMatrix(Xval, label= yval,missing = np.nan)
watchlist = [(dtr, 'train'), (dval, 'eval')]
history = dict()params = {
'max_depth': 26,
'eta': 0.025,
'nthread': 4,
'gamma' : 1,
'alpha' : 1,
'subsample': 0.85,
'eval_metric': ['auc'],
'objective': 'binary:logistic',
'colsample_bytree': 0.9,
'min_child_weight': 100,
'scale_pos_weight':(1)/y.mean(),
'seed':7
}model_new = xgb.train(params, dtr, num_boost_round=200, evals=watchlist, evals_result=history, verbose_eval=20)[0] train-auc:0.954886 eval-auc:0.85383
[20] train-auc:0.989848 eval-auc:0.910808
[40] train-auc:0.992086 eval-auc:0.916371
[60] train-auc:0.993658 eval-auc:0.917753
[80] train-auc:0.994874 eval-auc:0.918254
[100] train-auc:0.995743 eval-auc:0.917947
[120] train-auc:0.996396 eval-auc:0.917735
[140] train-auc:0.996964 eval-auc:0.918503
[160] train-auc:0.997368 eval-auc:0.919341
[180] train-auc:0.997682 eval-auc:0.920183Видим, что алгоритм сильно подстраивается под обучающую выборку, поэтому возможно наше предположение о необходимости использовать линейные алгоритмы подтверждено.
Посмотрим, что покажет обычный LogisticRegression.
from sklearn.linear_model import LogisticRegression
def get_auc_lr_valid(X, y, C=1, seed=7, ratio = 0.8):
# разделим выборку на обучающую и валидационную
idx = round(X.shape[0] * ratio)
# обучение классификатора
lr = LogisticRegression(C=C, random_state=seed, n_jobs=-1).fit(X[:idx], y[:idx])
# прогноз для валидационной выборки
y_pred = lr.predict_proba(X[idx:, :])[:, 1]
# считаем качество
score = roc_auc_score(y[idx:], y_pred)
return scoreget_auc_lr_valid(data_mean, y, C=1, seed=7, ratio = 0.8)0.90037148150108237Попробуем улучшить результаты.
Теперь вместо обычного среднего, чтобы учесть частоту с которой слово встречается в тексте, возьмем взвешенное среднее. В качестве весов возьмем IDF. Учёт IDF уменьшает вес широко употребительных слов и увеличивает вес более редких слов, которые могут достаточно точно указать на то, к какому классу относится текст. В нашем случае, кому принадлежит последовательность посещенных сайтов.
#пропишем класс выполняющий tfidf преобразование.
from sklearn.feature_extraction.text import TfidfVectorizer
from collections import defaultdict
class tfidf_vectorizer(object):
def __init__(self, word2vec):
self.word2vec = word2vec
self.word2weight = None
self.dim = len(next(iter(w2v.values())))
def fit(self, X):
tfidf = TfidfVectorizer(analyzer=lambda x: x)
tfidf.fit(X)
max_idf = max(tfidf.idf_)
self.word2weight = defaultdict(
lambda: max_idf,
[(w, tfidf.idf_[i]) for w, i in tfidf.vocabulary_.items()])
return self
def transform(self, X):
return np.array([
np.mean([self.word2vec[w] * self.word2weight[w]
for w in words if w in self.word2vec] or
[np.zeros(self.dim)], axis=0)
for words in X
])data_mean = tfidf_vectorizer(w2v).fit(train_df['list_w']).transform(train_df['list_w'])Проверим изменилось ли качество LogisticRegression.
get_auc_lr_valid(data_mean, y, C=1, seed=7, ratio = 0.8)0.90738924587178804видим прирост на 0.07, значит скорее всего взвешенное среднее помогает лучше отобразить смысл всего предложения через word2vec.
Предсказание популярности
Попробуем Word2Vec уже в текстовой задаче — предсказании популярности статьи на Хабрхабре.
Испробуем силы алгоритма непосредственно на текстовых данных статей Хабра. Мы преобразовали данные в csv таблицы. Скачать их вы можете здесь: train, test.
Xtrain = pd.read_csv('data/train_content.csv')
Xtest = pd.read_csv('data/test_content.csv')
print(Xtrain.shape,Xtest.shape)
Xtrain.head()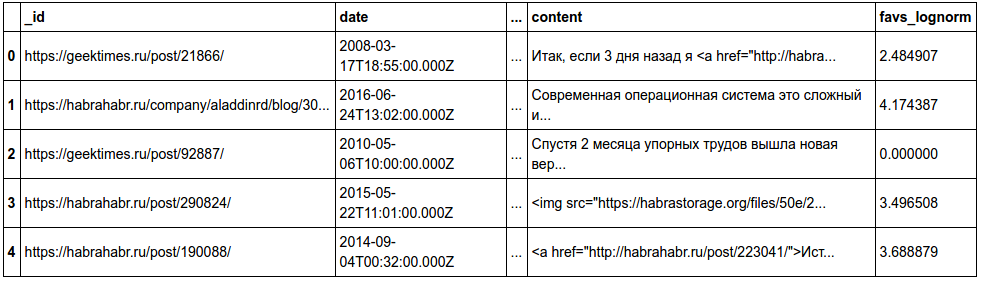
'Доброго хабрадня!
rn
rnПерейду сразу к сути. С недавнего времени на меня возложилась задача развития контекстной сети текстовых объявлений. Задача возможно кому-то покажется простой, но есть несколько нюансов. Страна маленькая, 90% интернет-пользователей сконцентрировано в одном городе. С одной стороны легко охватить, с другой стороны некуда развиваться.
rn
rnТак как развитие интернет-проектов у нас слабое, и недоверие клиентов к местным проектам преобладает, то привлечь рекламодателей тяжело. Но самое страшное это привлечь площадки, которые знают и Бегун и AdSense, но абсолютно не знают нас. В целом проблема такая: площадки не регистрируются, потому что нет рекламодателей с деньгами, а рекламодатели не дают объявления, потому что список площадок слаб.
rn
rnКак выходят из такого положения Хабраспециалисты?'
Будем обучать модель на всем содержании статьи. Для этого совершим некоторые преобразования над текстом.
Напишем функцию, которая будет преобразовывать тестовую статью в лист из слов необходимый для обучения Word2Vec.
Функция получает строку, в которой содержится весь текстовый документ.
1) Сначала функция будет удалять все символы кроме букв верхнего и нижнего регистра;
2) Затем преобразовывает слова к нижнему регистру;
3) После чего удаляет стоп слова из текста, т.к. они не несут никакой информации о содержании;
4) Лемматизация, процесс приведения словоформы к лемме — её нормальной (словарной) форме.
Функция возвращает лист из слов.
# подключим необходимые библиотеки
from sklearn.metrics import mean_squared_error
import re
from nltk.corpus import stopwords
import pymorphy2
morph = pymorphy2.MorphAnalyzer()
stops = set(stopwords.words("english")) | set(stopwords.words("russian"))
def review_to_wordlist(review):
#1)
review_text = re.sub("[^а-яА-Яa-zA-Z]"," ", review)
#2)
words = review_text.lower().split()
#3)
words = [w for w in words if not w in stops]
#4)
words = [morph.parse(w)[0].normal_form for w in words ]
return(words)
Лемматизация занимает много времени, поэтому ее можно убрать в целях более быстрых подсчетов.
# Преобразуем время
Xtrain['date'] = Xtrain['date'].apply(pd.to_datetime)
Xtrain['year'] = Xtrain['date'].apply(lambda x: x.year)
Xtrain['month'] = Xtrain['date'].apply(lambda x: x.month)Будем обучаться на 2015 году, а валидироваться по первым 4 месяцам 2016, т.к. в нашей тестовой выборке представлены данные за первые 4 месяца 2017 года. Более правдивую валидацию можно сделать, идя по годам, увеличивая нашу обучающую выборку и смотря качество на первых четырех месяцах следующего года
Xtr = Xtrain[Xtrain['year']==2015]
Xval = Xtrain[(Xtrain['year']==2016)& (Xtrain['month']<=4)]
ytr = Xtr['favs_lognorm']
yval = Xval['favs_lognorm']
Xtr.shape,Xval.shape,ytr.mean(),yval.mean()((23425, 15), (7556, 15), 3.4046228249071526, 3.304679829935242)data = pd.concat([Xtr,Xval],axis = 0,ignore_index = True)#у нас есть nan, поэтому преобразуем их к строке
data['content_clear'] = data['content'].apply(str)%%time
data['content_clear'] = data['content_clear'].apply(review_to_wordlist)model = word2vec.Word2Vec(data['content_clear'], size=300, window=10, workers=4)
w2v = dict(zip(model.wv.index2word, model.wv.syn0))Посмотрим чему выучилась модель:
model.wv.most_similar(positive=['open', 'data','science','best'])[('massive', 0.6958945393562317),
('mining', 0.6796239018440247),
('scientist', 0.6742461919784546),
('visualization', 0.6403135061264038),
('centers', 0.6386666297912598),
('big', 0.6237790584564209),
('engineering', 0.6209672689437866),
('structures', 0.609510600566864),
('knowledge', 0.6094595193862915),
('scientists', 0.6050446629524231)]
Модель обучилась достаточно неплохо, посмотрим на результаты алгоритмов:
data_mean = mean_vectorizer(w2v).fit(data['content_clear']).transform(data['content_clear'])
data_mean.shapedef split(train,y,ratio):
idx = ratio
return train[:idx, :], train[idx:, :], y[:idx], y[idx:]
y = data['favs_lognorm']
Xtr, Xval, ytr, yval = split(data_mean, y,23425)
Xtr.shape,Xval.shape,ytr.mean(),yval.mean()((23425, 300), (7556, 300), 3.4046228249071526, 3.304679829935242)from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
model = Ridge(alpha = 1,random_state=7)
model.fit(Xtr, ytr)
train_preds = model.predict(Xtr)
valid_preds = model.predict(Xval)
ymed = np.ones(len(valid_preds))*ytr.median()
print('Ошибка на трейне',mean_squared_error(ytr, train_preds))
print('Ошибка на валидации',mean_squared_error(yval, valid_preds))
print('Ошибка на валидации предсказываем медиану',mean_squared_error(yval, ymed))Ошибка на трейне 0.734248488422
Ошибка на валидации 0.665592676973
Ошибка на валидации предсказываем медиану 1.44601638512data_mean_tfidf = tfidf_vectorizer(w2v).fit(data['content_clear']).transform(data['content_clear'])y = data['favs_lognorm']
Xtr, Xval, ytr, yval = split(data_mean_tfidf, y,23425)
Xtr.shape,Xval.shape,ytr.mean(),yval.mean()((23425, 300), (7556, 300), 3.4046228249071526, 3.304679829935242)model = Ridge(alpha = 1,random_state=7)
model.fit(Xtr, ytr)
train_preds = model.predict(Xtr)
valid_preds = model.predict(Xval)
ymed = np.ones(len(valid_preds))*ytr.median()
print('Ошибка на трейне',mean_squared_error(ytr, train_preds))
print('Ошибка на валидации',mean_squared_error(yval, valid_preds))
print('Ошибка на валидации предсказываем медиану',mean_squared_error(yval, ymed))Ошибка на трейне 0.743623730976
Ошибка на валидации 0.675584372744
Ошибка на валидации предсказываем медиану 1.44601638512Попробуем нейронные сети.
# подключим библиотеки keras
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Activation, Input
from keras.preprocessing.text import Tokenizer
from keras import regularizers
from keras.wrappers.scikit_learn import KerasRegressor# Опишем нашу сеть.
def baseline_model():
model = Sequential()
model.add(Dense(128, input_dim=Xtr.shape[1], kernel_initializer='normal', activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1, kernel_initializer='normal'))
model.compile(loss='mean_squared_error', optimizer='adam')
return model
estimator = KerasRegressor(build_fn=baseline_model,epochs=20, nb_epoch=20, batch_size=64,validation_data=(Xval, yval), verbose=2)estimator.fit(Xtr, ytr)Train on 23425 samples, validate on 7556 samples
Epoch 1/20
1s — loss: 1.7292 — val_loss: 0.7336
Epoch 2/20
0s — loss: 1.2382 — val_loss: 0.6738
Epoch 3/20
0s — loss: 1.1379 — val_loss: 0.6916
Epoch 4/20
0s — loss: 1.0785 — val_loss: 0.6963
Epoch 5/20
0s — loss: 1.0362 — val_loss: 0.6256
Epoch 6/20
0s — loss: 0.9858 — val_loss: 0.6393
Epoch 7/20
0s — loss: 0.9508 — val_loss: 0.6424
Epoch 8/20
0s — loss: 0.9066 — val_loss: 0.6231
Epoch 9/20
0s — loss: 0.8819 — val_loss: 0.6207
Epoch 10/20
0s — loss: 0.8634 — val_loss: 0.5993
Epoch 11/20
1s — loss: 0.8401 — val_loss: 0.6093
Epoch 12/20
1s — loss: 0.8152 — val_loss: 0.6006
Epoch 13/20
0s — loss: 0.8005 — val_loss: 0.5931
Epoch 14/20
0s — loss: 0.7736 — val_loss: 0.6245
Epoch 15/20
0s — loss: 0.7599 — val_loss: 0.5978
Epoch 16/20
1s — loss: 0.7407 — val_loss: 0.6593
Epoch 17/20
1s — loss: 0.7339 — val_loss: 0.5906
Epoch 18/20
1s — loss: 0.7256 — val_loss: 0.5878
Epoch 19/20
1s — loss: 0.7117 — val_loss: 0.6123
Epoch 20/20
0s — loss: 0.7069 — val_loss: 0.5948
Получили более хороший результат по сравнению с гребневой регрессией.
Заключение
Word2Vec показал свою пользу на практических задачах анализа текстов, все-таки не зря на текущий момент на практике используется в основном именно он и — гораздо менее популярный — GloVe. Тем не менее, может быть в вашей конкретной задаче, вам пригодятся подходы, которым для эффективной работы не требуются такие объемы данных, как для word2vec.
Код ноутбуков с примерами можно взять здесь. Код практического применения — вот тут.
Пост написан совместно с demonzheg.
Литература
- Tomas Mikolov, Kai Chen, Greg Corrado, and Jeffrey Dean. Efficient estimation
of word representations in vector space. CoRR, abs/1301.3781, - Tomas Mikolov, Ilya Sutskever, Kai Chen, Gregory S. Corrado, and Jeffrey Dean. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013. Proceedings of a meeting held December 5-8, 2013, Lake Tahoe, Nevada, United States, pages 3111–3119, 2013.
- Morin, F., & Bengio, Y. Hierarchical Probabilistic Neural Network Language Model. Aistats, 5, 2005.
- Jeffrey Pennington, Richard Socher, and Christopher D. Manning. GloVe: Global Vectors for Word Representation. 2014.
- Piotr Bojanowski, Edouard Grave, Armand Joulin, and Tomas Mikolov. Enriching word vectors
with subword information. arXiv preprint arXiv:1607.04606, 2016.
* Да, это специальная пасхалка для любителей творчества Энтони Бёрджеса.
Автор: madrugado







