Простая модель адаптивного фильтра Калмана средствами Python

Проблема

Вечная проблема любых измерений их низкая точность. Основных способов повышения точности два, первый состоит в повышении чувствительности к измеряемой величине, однако при этом как правило растёт чувствительность и к неинформативным параметрам, что требует принятия дополнительных мер по их компенсации. Второй способ состоит в статистической обработке многократных измерений, при этом дисперсия среднего обратно пропорциональна корню квадратному из числа измерений.

Статистические методы повышения точности разнообразны и многочисленны, но и они делятся на пассивные для статических измерений и активные для динамических измерений, когда измеримая величина изменяется во времени. При этом сама измеряемая величина так же, как и помеха являются случайными величинами с изменяющимися дисперсиями.

Адаптивность методов повышения точности динамических измерений следует понимать, как использование прогнозирования значений дисперсий и погрешности для следующего цикла измерений.Такое прогнозирование осуществляется в каждом цикле измерений. Для этой цели применяются фильтры Винера, работающие в частотной области. В отличии от фильтра Винера, фильтр Калмана работает во временной, а не в частотной области. Фильтр Калмана был разработан для многомерных задач, формулировка которых осуществляется в матричной форме. Матричная форма достаточно подробно описана для реализации на Python в статье [1], [2]. Описание работы фильтра Калмана, приведенная в указанных статьях, рассчитана на специалистов в области цифровой фильтрации. Поэтому возникла необходимость рассмотреть работу фильтра Калмана в более простой скалярной форме.

Немного теории

Рассмотрим схему фильтра Калмана для его дискретной формы.

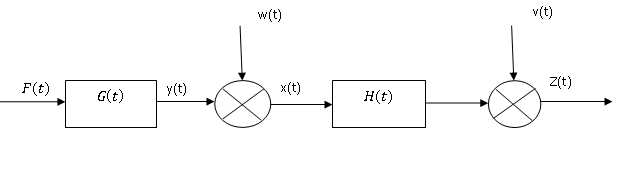
Здесь G(t) блок работа которого описывается линейными соотношениями. На выходе блока вырабатывается неслучайный сигнал y(t). Этот сигнал суммируется с шумом w(t), который возникает внутри контролируемого объекта. В результате такого сложения, получаем новый сигнал x(t). Этот сигнал представляет сумму неслучайного сигнала и шума и является случайный сигналом. Далее сигнал x(t) преобразуется линейным блоком H(t), суммируясь с шумом v(t), распределённым по-другому чем w(t) закону. На выходе линейного блока H(t) получаем случайный сигнал z(t), по которому и определяется неслучайный сигнал y(t). Следует отметить, что линейные функции блоков G(t) и Н(t) могут тоже зависеть от времени.

Будем считать, что случайные шумы w(t) и v(t) — это случайные процессы с дисперсиями Q, R и нулевыми математическими ожиданиями. Сигнал x(t) после линейного преобразования в блоке G(t) распределён во времени по нормальному закону. С учётом изложенного, соотношение для измеряемого сигнала примет вид:

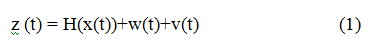
Постановка задачи

После фильтра нужно получить максимально возможное приближение y'' к неслучайному сигналу y(t).

При непрерывном динамическом измерении каждое следующее состояние объекта, а, следовательно, и значение контролируемой величины отличается от предыдущего по экспоненциальному закону с постоянного времени T в текущем интервале времени ,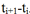

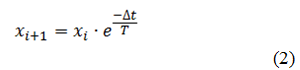
Ниже приведена программа на Python, в которой решается уравнение для неизвестного не зашумлённого сигнала y(t). Процесс измерения рассматривается для суммы двух псевдослучайных величин, каждая из которых образуется как функция нормального распределения от равномерного распределения.

#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import numpy as np
from numpy import exp,sqrt
from scipy.stats import norm
Q=0.8;R=0.2;y=0;x=0#начальные дисперсии шумов(выбраны произвольно) и нулевые значения  переменных.
P=Q*R/(Q+R)# первая оценка дисперсий шумов.
T=5.0#постоянная времени.
n=[];X=[];Y=[];Z=[]#списки для переменных.
for i in np.arange(0,100,0.2):
                n.append(i)#переменная времени.    
                x=1-exp(-1/T)+x*exp(-1/T)#модельная функция для x.
                y=1-exp(-1/T)+y*exp(-1/T)# модельная функция для y.
                Y.append(y)#накопление списка значений y.
                X.append(x)# накопление списка значений x.
                norm1 = norm(y, sqrt(Q))# нормальное распределение с #математическим ожиданием – y.
                norm2 = norm(0, sqrt(R))# ))# нормальное распределение с #математическим ожиданием – 0.
                ravn1=np.random.uniform(0,2*sqrt(Q))#равномерное распределение #для шума с дисперсией Q.
                ravn2=np.random.uniform(0,2*sqrt(R))# равномерное распределение #для шума с дисперсией R.
                z=norm1.pdf( ravn1)+norm2.pdf( ravn2)#измеряемая переменная z.
                Z.append(z)# накопление списка значений z.
                P=P-(P**2)/(P+Q+R) #переход в новое состояние для x.
                x=(P*z+x*R)/(P+R)# новое состояние x.
                P=(P*R)/(P+R)# прогноз для нового состояния x.
plt.plot(n, Y, color='g',linewidth=4, label='Y')
plt.plot(n, X, color='r',linewidth=4, label='X')
plt.plot(n, Z, color='b', linewidth=1, label='Z')
plt.legend(loc='best')
plt.grid(True)
plt.show()

В чём отличие предложенного алгоритма от известного

Мною был усовершенствован алгоритм работы фильтра Калмана, приведенный в методических указаниях [3] для Mathcad:

В результате преждевременной смены состояния для сравниваемой переменной x(t) возрастала погрешность на участке резких изменений:

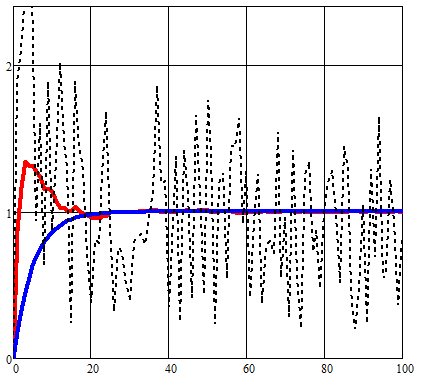
Тогда как в моем алгоритме используется начальная прогнозная оценка влияния шумов. Это дало возможность уменьшить ошибку измерений v(t).

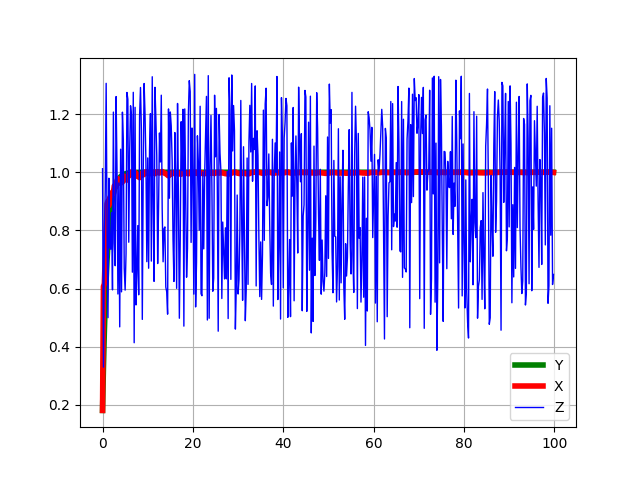
В приведённом алгоритме используются заданные – модельные экспоненциальные функции, поэтому для наглядности приведём их отдельно на общем графике работы фильтра Калмана.

#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import numpy as np
from numpy import exp,sqrt
from scipy.stats import norm
Q=0.8;R=0.2;y=0;x=0#начальные дисперсии шумов(выбраны произвольно) и нулевые значения  переменных.
P=Q*R/(Q+R)# первая оценка дисперсий шумов.
T=5.0#постоянная времени.
n=[];X=[];Y=[];Z=[]#списки для переменных.
for i in np.arange(0,100,0.2):
                n.append(i)#переменная времени.    
                x=1-exp(-1/T)+x*exp(-1/T)#модельная функция для x.
                y=1-exp(-1/T)+y*exp(-1/T)# модельная функция для y.
                Y.append(y)#накопление списка значений y.
                X.append(x)# накопление списка значений x.
                norm1 = norm(y, sqrt(Q))# нормальное распределение с #математическим ожиданием – y.
                norm2 = norm(0, sqrt(R))# ))# нормальное распределение с #математическим ожиданием – 0.
                ravn1=np.random.uniform(0,2*sqrt(Q))#равномерное распределение #для шума с дисперсией Q.
                ravn2=np.random.uniform(0,2*sqrt(R))# равномерное распределение #для шума с дисперсией R.
                z=norm1.pdf( ravn1)+norm2.pdf( ravn2)#измеряемая переменная z.
                Z.append(z)# накопление списка значений z.
                P=P-(P**2)/(P+Q+R) #переход в новое состояние для x.
                x=(P*z+x*R)/(P+R)# новое состояние x.
                P=(P*R)/(P+R)# прогноз для нового состояния x.
plt.subplot(221)
plt.plot(n, Y, color='g',linewidth=2, label='Модельная функция n не зашумленой n переменной')
plt.legend(loc='best')
plt.grid(True)
plt.subplot(222)
plt.plot(n, X, color='r',linewidth=2, label='Модельная функция n  сравниваемой n переменной')
plt.legend(loc='best')
plt.grid(True)
plt.subplot(223)
plt.plot(n, Z, color='b', linewidth=1, label='Измеряемая функция n псевдослучайных переменных')
plt.legend(loc='best')
plt.grid(True)
plt.subplot(224)
plt.plot(n, Y, color='g',linewidth=2, label='Y')
plt.plot(n, X, color='r',linewidth=2, label='X')
plt.plot(n, Z, color='b', linewidth=1, label='Z')
plt.legend(loc='best')
plt.grid(True)
plt.show()

Результат работы программы

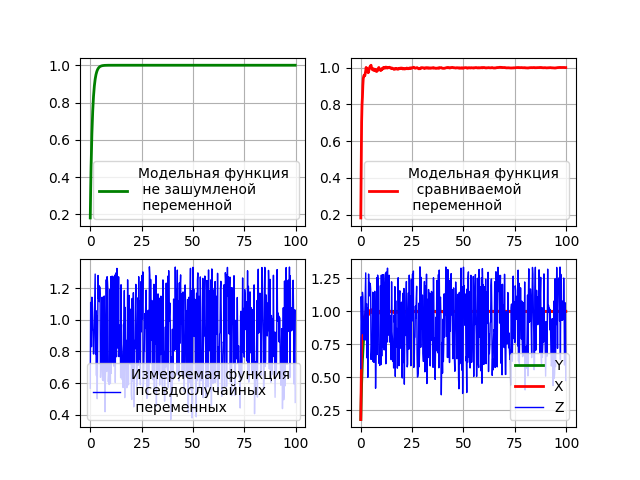
Выводы

В статье описана модель простой скалярной реализации фильтра Калмана средствами условно бесплатного языка программирования общего назначения Python, что расширит область её применения в целях обучения.

Ссылки

1. Использование фильтра Калмана для определения производных измеряемой величины.
2. Kalman Filtering in Python for Reading Sensor Input.
3. Адаптивный фильтр Калмана.

Автор: Scorobey

Источник