Моделирование электрической цепи

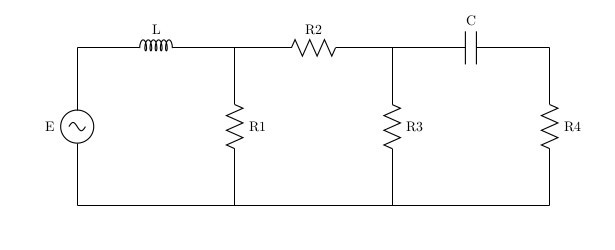
В данной публикации представлена инструкция по моделированию электрической цепи методом переменных состояния.

Эта публикация для того, чтобы был на русском языке хотя бы один how2 по моделированию электрических схем этим методом. В своё время я очень много гуглил и ни разу мне не попадалось нормального материала. Все методички и учебники содержали в себе только теорию. Вдобавок ни в одном, из найденных мной материалов, не было полного цикла решения: схема⟶уравнения⟶численное решение⟶графики. Собственно, это и есть алгоритм действий.

Схема есть, теперь нужно составить уравнения, используя законы Ома и Кирхгофа.

Компонентные уравнения:

Контурные уравнения:

Узловые уравнения:

Теперь нужно вывести дифференциальные уравнения. Отмечу, что в этом методе за переменные состояния принято брать заряды конденсаторов и потокосцепления индуктивностей. Зная эти величины, можно вывести любые напряжения и токи узлов и ветвей. Также:

1. Уравнения должны быть независимыми;
2. В уравнения должны входить только переменные состояния и источников; все остальные переменные должны быть выражены через переменные состояния;
3. В левую часть каждого уравнения должна войти первая производная из переменных состояния; в правой части не должно быть производных.

Выведем первое дифференциальное уравнение:

Выведем второе дифференциальное уравнение:

Теперь у нас есть система дифференциальных уравнений, которые можно решить численно:

Воспользуемся методом Эйлера т.к. он самый простой и воспользуемся Python:

import numpy as np
import matplotlib.pyplot as plt

#Input voltage amplitude
AMP = 21.0

#Active components
r1 = 2000.0; r2 = 10.0; r3 = 10.0; r4 =2000.0;

#Reactive components
c=0.0001; l=0.06;

#Time components
T=0.01; t0=0.0; step=T/1000;
tf=T*10

steps=int(tf/step);

#Input voltage
def E(t):
    n=int(t/T)
    if ((t >= n*T )and(t <= n*T + T/2)):
        return AMP
    else:
        return 0.0


time = np.arange(t0, tf, step)

ul = []; il = []; uc = []; ic = []; y = [];

for i in range(0, steps, 1):
    y.append(E(time[i]))

def dIl_dt(t):
    return float((1.0/l)*(E(t) - (r2+r3)*il[int(t/step)]*r1/(r1+r2+r3)))

def dUc_dt(t):
    return float((1.0/c)*((r3*r1*il[int(t/step)]/(r1+r2+r3) - uc[int(t/step)])/r4))

#Uc
def Uc(t):
    return float((il[int(t/step)] - ic[int(t/step)])*r3 - ic[int(t/step)]*r4)
#Il
def Il(t):
    return float(((E(t)-ul[int(t/step)])*(r1*(r2+r3) + r1)/(r1*r1*(r2+r3))) + ic[int(t/step)])

#Start condition
ul.append(E(0)); il.append(0.0); uc.append(0.0); ic.append(0.0);

#Euler method
for i in range(1, steps, 1):
    il.append(il[i-1] + step*dIl_dt(time[i-1]))
    uc.append(uc[i-1] + step*dUc_dt(time[i-1]))
    ul.append(l*dIl_dt(time[i]))
    ic.append(c*dUc_dt(time[i]))

plt.figure("charts")
e = plt.subplot(311)
e.plot(time, y)
e.set_xlabel('time (s)')
e.set_ylabel('E(t), (V)', color='b')
plt.grid(True)

UL = plt.subplot(312)
UL.plot(time, ul)
UL.set_xlabel('time (s)')
UL.set_ylabel('Ul(t), (V)', color = 'b')

IL = UL.twinx()
IL.plot(time, il, 'r')
IL.set_ylabel('Il(t), (A)', color = 'r')
plt.grid(True)

UC = plt.subplot(313)
UC.plot(time, uc)
UC.set_xlabel('time (s)')
UC.set_ylabel('Uc(t), (V)', color = 'b')

IC = UC.twinx()
IC.plot(time, ic, color = 'r')
IC.set_ylabel('Ic(t), (A)', color = 'r')
plt.grid(True)

plt.show()

Результаты моделирования:

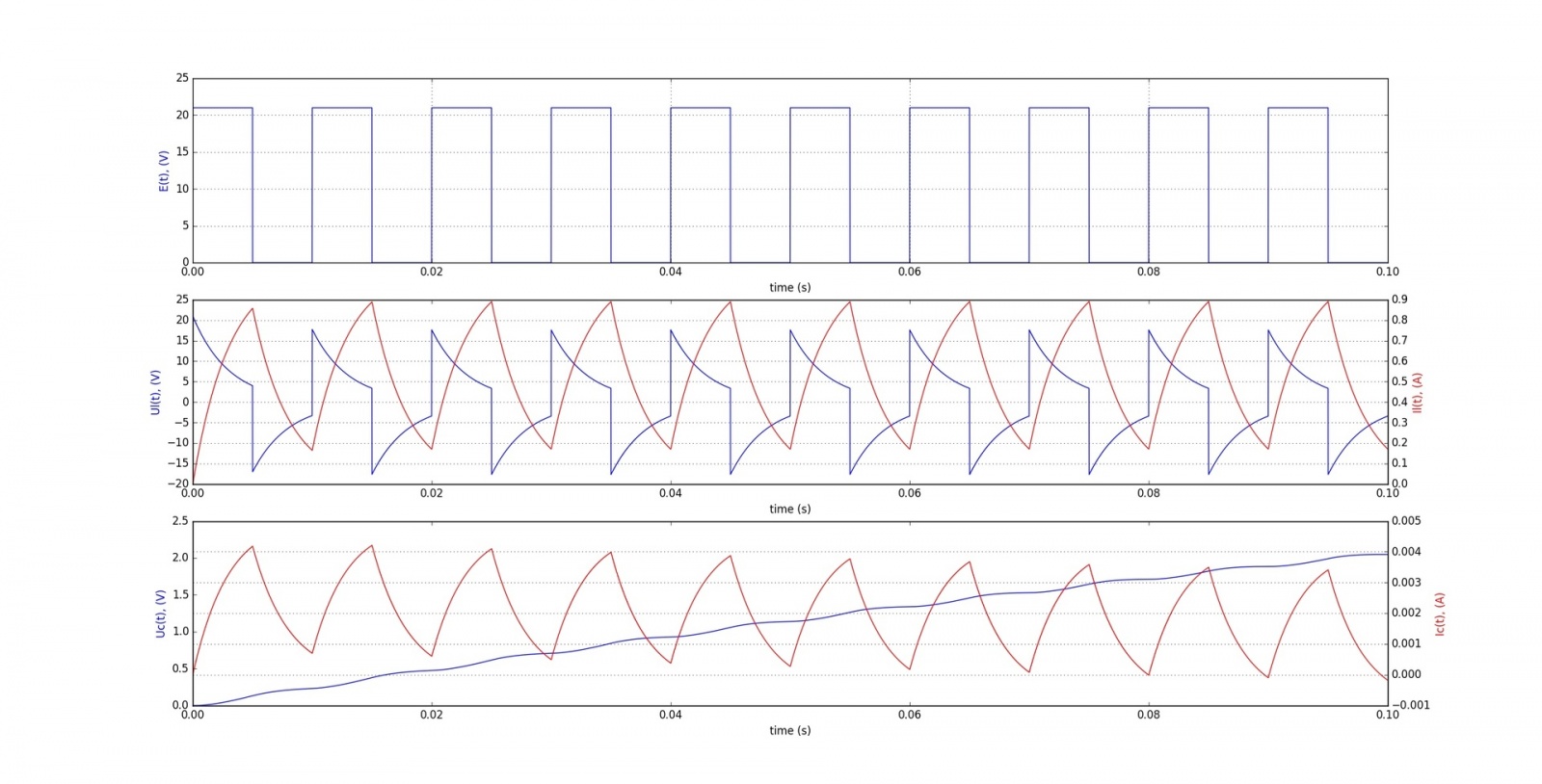
Использовать для реальных расчётов лучше другие методы решения дифур, а для получения графиков напряжений и токов элементов для самообучения достаточно и простейшего метода Эйлера. В электронике самый распространённый метод Ньютона-Рафсона- в большинстве САПР используется именно этот метод.

Из литературы советую книги Матханова П.Н. и Зевеке Г.В.
А методички всяких политехов (МГТУ, Питерский, Томский и т.п.) и подобный материал легче выкинуть, чем понять, что там написано. Здесь очень к месту крылатая фраза: «упрощять- сложно, усложнять- легко».

Автор: gazpar

Источник