Python обладает рядом привлекательных преимуществ к которым относится простота реализации программных решений, наглядность и лаконичность кода, наличие большого числа библиотек и многочисленного активного комьюнити. В то же время, известная всем медлительность питона часто ограничивает его применимость для “тяжелых” вычислений. Для ряда задач можно добиться существенного ускорения расчетов путем использования технологии CUDA для параллельных вычислений на GPU. Цель этого небольшого исследования — анализ возможностей эффективного использования python для расчетов на GPU и сравнение производительности различных python-решений с реализацией на C.
Введение
По роду деятельности я частенько занимаюсь задачами численного моделирования. Во многих случаях мы используем технологию CUDA для ускорения расчетов за счет использования возможностей параллельных вычислений на GPU, при этом программы пишутся на языке C. В то же время, в некоторых случаях хотелось бы иметь возможность реализовывать расчеты на питоне, потому что это удобно, быстро, гибко, лаконично, молодежно. При этом, однако, очень важно не терять в скорости выполнения программ, поскольку некоторые расчеты могут занимать от нескольких часов до суток. В статье продемонстрировано использование python-библиотек Numba и PyCUDA для реализации параллельных расчетов на GPU и приведены результаты сравнения их производительности на тестовой задаче.
Тестовая задача
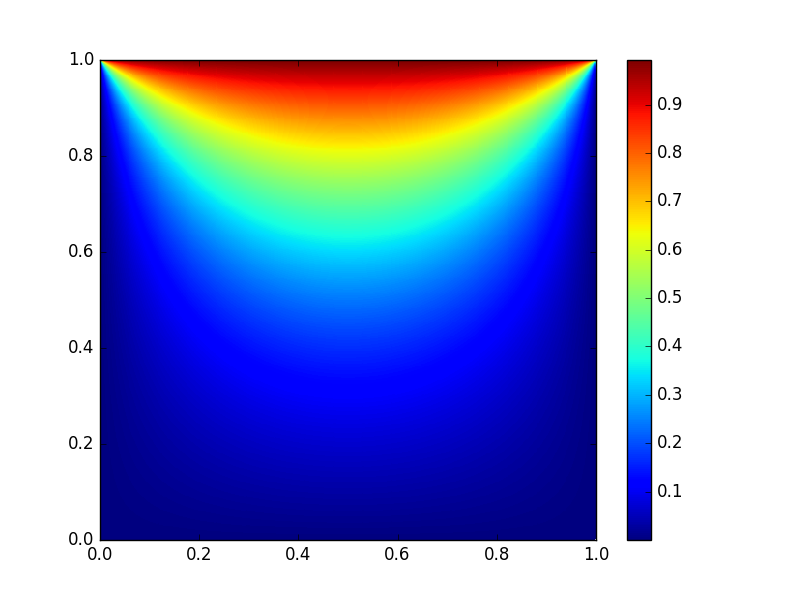
Выбор тестовой задачи и условий тестирования был обусловлен характером реальных задач, для решения которых в дальнейшем планируется использование python. При этом была выбрана максимально простая задача, а именно задача решения двумерного уравнения теплопроводности с помощью явной конечно-разностной схемы. Задача рассматривалась на квадратной области с заданными значениями температуры на границах. Количество узлов расчетной сетки по x и y одинаково и равно n. На рисунке в начале статьи показано установившееся решение тестовой задачи.
Алгоритм и условия тестирования
Алгоритм решения задачи можно представить следующим псевдокодом:
Инициализировать массивы u0 и u, хранящие значения решения на текущем и следующем временном шаге
включить таймер
выделить память на девайсе и скопировать массивы u0 и u с хоста на девайс
for(i = 0; i < nstp/2; i++)
вычислить значение u на следующем шаге по времени, зная значение u0 на текущем временном шаге
вычислить значение u0 на следующем шаге по времени, зная значение u на текущем временном шаге
скопировать результат (u0) с девайса на хост
выключить таймер и вывести результатВо всех тестах представленных ниже число узлов квадратной сетки в каждом направлении (n) варьировалось от 512 до 4096, а nstp = 5000.
Программное и аппаратное обеспечение
Тестирование проводилось на персональном компьютере:
Intel® Core(TM)2 Quad CPU Q9650 @ 3.00GHz, 8 Gb ОЗУ
GPU: Nvidia GTX 580
Операционная система: Ubuntu 16.04 LTS с установленной CUDA 7.5
Реализация на C
Все дальнейшие python-реализации сравнивались с результатами, полученными с помощью программы на C, описанной в этом разделе.
#include <stdio.h>
#include <time.h>
#include <cuda_runtime.h>
#define BLOCK_SIZE 16
int N = 512; //1024; //2048;
double L = 1.0;
double h = L/N;
double h2 = h*h;
double tau = 0.1*h2;
double th2 = tau/h2;
int nstp = 5000;
__constant__ int dN;
__constant__ double dth2;
__global__ void NextStpGPU(double *u0, double *u)
{
int i = blockDim.x * blockIdx.x + threadIdx.x;
int j = blockDim.y * blockIdx.y + threadIdx.y;
double uim1, uip1, ujm1, ujp1, u00, d2x, d2y;
if (i > 0)
uim1 = u0[(i - 1) + dN*j];
else
uim1 = 0.0;
if (i < dN - 1)
uip1 = u0[(i + 1) + dN*j];
else
uip1 = 0.0;
if (j > 0)
ujm1 = u0[i + dN*(j - 1)];
else
ujm1 = 0.0;
if (j < dN - 1)
ujp1 = u0[i + dN*(j + 1)];
else
ujp1 = 1.0;
u00 = u0[i + dN*j];
d2x = (uim1 - 2.0*u00 + uip1);
d2y = (ujm1 - 2.0*u00 + ujp1);
u[i + dN*j] = u00 + dth2*(d2x + d2y);
}
int main(void)
{
size_t size = N * N * sizeof(double);
double pStart, pEnd, pD;
int i;
double *h_u0 = (double *)malloc(size);
double *h_u1 = (double *)malloc(size);
for (i = 0; i < N*N; ++i)
{
h_u0[i] = 0.0;
h_u1[i] = 0.0;
}
pStart = (double) clock();
double *d_u0 = NULL;
cudaMalloc((void **)&d_u0, size);
double *d_u1 = NULL;
cudaMalloc((void **)&d_u1, size);
cudaMemcpy(d_u0, h_u0, size, cudaMemcpyHostToDevice);
cudaMemcpy(d_u1, h_u1, size, cudaMemcpyHostToDevice);
cudaMemcpyToSymbol(dN, &N, sizeof(int));
cudaMemcpyToSymbol(dth2, &th2, sizeof(double));
dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE, 1);
dim3 dimGrid(N/BLOCK_SIZE, N/BLOCK_SIZE, 1);
for(i = 0; i < int(nstp/2); i++)
{
NextStpGPU<<<dimGrid,dimBlock>>>(d_u0, d_u1);
NextStpGPU<<<dimGrid,dimBlock>>>(d_u1, d_u0);
}
cudaMemcpy(h_u0, d_u0, size, cudaMemcpyDeviceToHost);
cudaFree(d_u0);
cudaFree(d_u1);
pEnd = (double) clock();
pD = (pEnd-pStart)/CLOCKS_PER_SEC;
printf("Calculation time on GPU = %f secn", pD);
}
free(h_u0);
free(h_u1);
return 0;
}
Расчеты показывают, что для N = 512 время выполнения C-программы распараллеленной на GPU составляет 0.27 секунд против 33.06 секунд для последовательной реализации алгоритма на CPU. То есть ускорение CPU/GPU составляет около 120 раз. С ростом N величина ускорения не убывает.
Python with Numba
Библиотека Numba предоставляет возможность jit (just-in-time) компиляции кода на питоне в байт-код сравнимый по производительности с C или Fortran кодом. Numba поддерживает компиляцию и запуск python-кода не только на CPU, но и на GPU, при этом стиль и вид программы, использующей библиотеку Numba, остается чисто питоновским.
from numba import cuda
import numpy as np
import matplotlib.pyplot as plt
from time import time
n = 512
blockdim = 16, 16
griddim = int(n/blockdim[0]), int(n/blockdim[1])
L = 1.
h = L/n
dt = 0.1*h**2
nstp = 5000
@cuda.jit("void(float64[:,:], float64[:,:])")
def nextstp_gpu(u0, u):
i,j = cuda.grid(2)
if i > 0:
uim1 = u0[i-1,j]
else:
uim1 = 0.
if i < n-1:
uip1 = u0[i+1,j]
else:
uip1 = 0.
if j > 0:
ujm1 = u0[i,j-1]
else:
ujm1 = 0.
if j < n-1:
ujp1 = u0[i,j+1]
else:
ujp1 = 1.
d2x = (uim1 - 2.*u0[i,j] + uip1)
d2y = (ujm1 - 2.*u0[i,j] + ujp1)
u[i,j] = u0[i,j] + (dt/h**2)*(d2x + d2y)
u0 = np.full((n,n), 0., dtype = np.float64)
u = np.full((n,n), 0., dtype = np.float64)
st = time()
d_u0 = cuda.to_device(u0)
d_u = cuda.to_device(u)
for i in xrange(0, int(nstp/2)):
nextstp_gpu[griddim,blockdim](d_u0, d_u)
nextstp_gpu[griddim,blockdim](d_u, d_u0)
cuda.synchronize()
u0 = d_u0.copy_to_host()
print 'time on GPU = ', time() - st
Отметим тут несколько приятных особенностей. Во-первых, эта реализация намного короче и нагляднее. Здесь мы использовали двумерные массивы, что делает код намного более удобочитаемым. Во-вторых, если в C-реализации от нас требовалось передать все константы (например N) путем исполнения функций вроде cudaMemcpyToSymbol(dN, &N, sizeof(int)); то здесь мы просто пользуемся глобальными переменными как в обычной python-функции. Ну и наконец, реализация не требует никаких знаний языка C и архитектуры GPU.
Этот код легко переписать и для случая использования одномерных массивов размера n*n, как будет показано далее это существенно влияет на скорость выполнения.
from numba import cuda
import numpy as np
import matplotlib.pyplot as plt
from time import time
n = 512
blockdim = 16, 16
griddim = int(n/blockdim[0]), int(n/blockdim[1])
L = 1.
h = L/n
dt = 0.1*h**2
nstp = 5000
@cuda.jit("void(float64[:], float64[:])")
def nextstp_gpu(u0, u):
i,j = cuda.grid(2)
u00 = u0[i + n*j]
if i > 0:
uim1 = u0[i-1 + n*j]
else:
uim1 = 0.
if i < n-1:
uip1 = u0[i+1 + n*j]
else:
uip1 = 0.
if j > 0:
ujm1 = u0[i + n*(j-1)]
else:
ujm1 = 0.
if j < n-1:
ujp1 = u0[i + n*(j+1)]
else:
ujp1 = 1.
d2x = (uim1 - 2.*u00 + uip1)
d2y = (ujm1 - 2.*u00 + ujp1)
u[i + n*j] = u00 + (dt/h/h)*(d2x + d2y)
u0 = np.full(n*n, 0., dtype = np.float64)
u = np.full(n*n, 0., dtype = np.float64)
st = time()
d_u0 = cuda.to_device(u0)
d_u = cuda.to_device(u)
for i in xrange(0, int(nstp/2)):
nextstp_gpu[griddim,blockdim](d_u0, d_u)
nextstp_gpu[griddim,blockdim](d_u, d_u0)
cuda.synchronize()
u0 = d_u0.copy_to_host()
print 'time on GPU = ', time() - st
PyCUDA
Второй из протестированных python-библиотек была библиотека PyCUDA. В отличии от Numba здесь от разработчика потребуется написать код ядра на C, поэтому без знания этого языка не обойтись. С другой стороны кроме собственно ядра на C ничего писать не надо.
import pycuda.driver as cuda
import pycuda.autoinit
from pycuda.compiler import SourceModule
import numpy as np
import matplotlib.pyplot as plt
from time import time
n = 512
blockdim = 16, 16
griddim = int(n/blockdim[0]), int(n/blockdim[1])
L = 1.
h = L/n
dt = 0.1*h**2
nstp = 5000
mod = SourceModule("""
__global__ void NextStpGPU(int* dN, double* dth2, double *u0, double *u)
{
int i = blockDim.x * blockIdx.x + threadIdx.x;
int j = blockDim.y * blockIdx.y + threadIdx.y;
double uim1, uip1, ujm1, ujp1, u00, d2x, d2y;
uim1 = exp(-10.0);
if (i > 0)
uim1 = u0[(i - 1) + dN[0]*j];
else
uim1 = 0.0;
if (i < dN[0] - 1)
uip1 = u0[(i + 1) + dN[0]*j];
else
uip1 = 0.0;
if (j > 0)
ujm1 = u0[i + dN[0]*(j - 1)];
else
ujm1 = 0.0;
if (j < dN[0] - 1)
ujp1 = u0[i + dN[0]*(j + 1)];
else
ujp1 = 1.0;
u00 = u0[i + dN[0]*j];
d2x = (uim1 - 2.0*u00 + uip1);
d2y = (ujm1 - 2.0*u00 + ujp1);
u[i + dN[0]*j] = u00 + dth2[0]*(d2x + d2y);
}
""")
u0 = np.full(n*n, 0., dtype = np.float64)
u = np.full(n*n, 0., dtype = np.float64)
nn = np.full(1, n, dtype = np.int64)
th2 = np.full(1, dt/h/h, dtype = np.float64)
st = time()
u0_gpu = cuda.to_device(u0)
u_gpu = cuda.to_device(u)
n_gpu = cuda.to_device(nn)
th2_gpu = cuda.to_device(th2)
func = mod.get_function("NextStpGPU")
for i in xrange(0, int(nstp/2)):
func(n_gpu, th2_gpu, u0_gpu, u_gpu,
block=(blockdim[0],blockdim[1],1),grid=(griddim[0],griddim[1],1))
func(n_gpu, th2_gpu, u_gpu, u0_gpu,
block=(blockdim[0],blockdim[1],1),grid=(griddim[0],griddim[1],1))
u0 = cuda.from_device_like(u0_gpu, u0)
print 'time on GPU = ', time() - st
Выглядит это все как чистый питон за исключением локальной вставки C-кода.
Сравнение производительности
На Рисунке 1 и в Таблице 1 приведены зависимости времени выполнения тестовой программы (в секундах) от размера сетки n, полученные при запуске C-кода (кривая CUDA C) и python-реализаций с библиотекой Numba и двумерными массивами (Numba 2DArr), с библиотекой Numba и одномерными массивами (Numba 1DArr), с библиотекой PyCUDA (кривая PyCUDA).
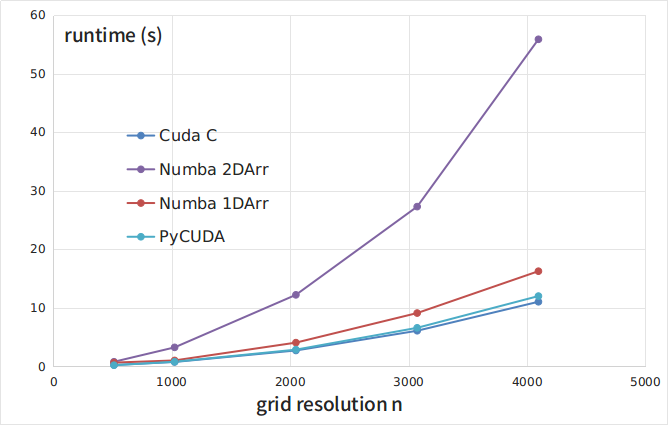
Рисунок 1
| n | Cuda C | Numba 2DArr | Numba 1DArr | PyCUDA |
|---|---|---|---|---|
| 512 | 0.25 | 0.8 | 0.66 | 0.216 |
| 1024 | 0.77 | 3.26 | 1.03 | 0.808 |
| 2048 | 2.73 | 12.23 | 4.07 | 2.87 |
| 3073 | 6.1 | 27.3 | 9.12 | 6.6 |
| 4096 | 11.05 | 55.88 | 16.27 | 12.02 |
На Рисунке 2 приведены отношения времени выполнения различных python-реализаций к времени выполнения C-кода. Как видно из рисунков, самой медленной, из рассмотренных, является реализация с помощью библиотеки Numba с использованием двумерных массивов. При этом, этот подход является самым наглядным и простым. Интересно, что развертка двумерных массивов в одномерные приводит к примерно троекратному ускорению кода. Самым быстрым решением оказалось использование библиотеки PyCUDA. В то же время, как отмечалось выше, использование этой библиотеки несколько более трудоемко, поскольку требует написания ядра на C. Однако затраты окупаются и скорость выполнения такой python-программы всего на 5-8% меньше чем программы, написанной полностью на C.
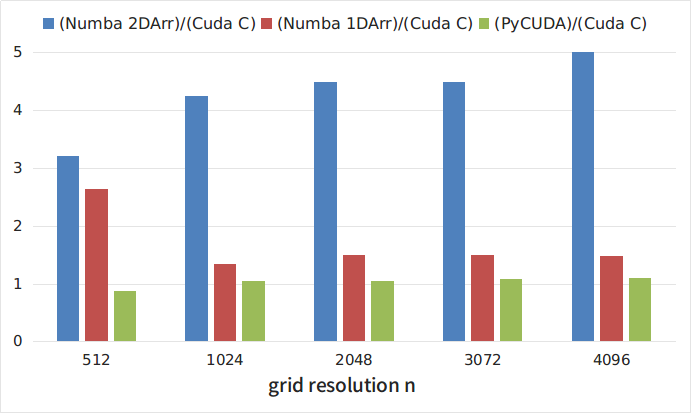
Рисунок 2
Выводы
Чудес не бывает и самые простые и наглядные решения оказываются одновременно и самыми медленными. В то же время, имеющиеся библиотеки позволяют добиться скорости выполнения python-программ, сравнимой со скоростью выполнения чистого C-кода. Существующие библиотеки дают разработчику выбор между более и менее высокоуровневыми решениями. Этот выбор, однако, всегда есть компромисс между скоростью разработки и скоростью выполнения программы.
Ссылки
» Документация библиотеки Numba
» Примеры использования Numba
» Документация библиотеки PyCUDA
» Примеры использования PyCUDA
Автор: f_rom