«Сферический трейдер в вакууме»: инструкция по применению

Если проанализировать форумов о рынках (в том числе Форекс), можно выделить два достаточно устойчивых мнения, назовём их пессимистическим и оптимистическим:

Пессимисты утверждают: рынок случаен «потому что я построил график случайного процесса и мой друг (профессиональный трейдер) не смог отличить его от графика EURUSD», а значит иметь стабильный доход на рынке( на Форекс) невозможно по определению!

Оптимисты им возражают: если бы рынок был случаен, котировки не гуляли бы в окрестности 1, а ушли в бесконечность. Значит рынок неслучаен и на нём можно зарабатывать. Я видел реально стабильно зарабатывающую стратегию с большим профит-фактором (больше стольки-то)!

Попробуем остаться реалистами и извлечь пользу из обоих мнений: предположим, что рынок случаен, и на основании этого предположения построим методику проверки доходности торговой системы на неслучайность.

---

Рассматриваемые в статье методики универсальны для любых рынков, будь то фонд, Форекс или любой другой!

---

Постановка задачи

Благодаря известному анекдоту про сферического коня в вакууме родилась замечательная аллегория, означающая идеальную, но совершенно неприменимую на практике модель.

Тем не менее, при правильной постановке задачи можно извлечь вполне ощутимую практическую пользу, применяя «сферическую модель в вакууме». Например, через отрицание «сферичности» реального объекта исследования.

Предположим, что у нас есть торговая система, используемая на некотором рынке. Также предположим, что рынок не случаен и система использует для принятия торговых решений что-то не являющееся замаскированным под индикаторы генератором случайных чисел. Для оценки стабильности дохода используем профит-фактор: , где — сумма дохода, а — сумма убытка (положительное число).

Каким должен быть профит-фактор, чтобы можно было говорить о стабильности данной системы? Очевидно, что чем профит-фактор выше, тем больше поводов доверять системе. А вот нижняя граница оценивается разными специалистами по разному. Наиболее популярные варианты: > 2 (так себе), > 5 (хорошая система), > 10 (отличная система). Ещё встречается такая вариация: , где — максимальное значение дохода по сделке, такая величина называется достоверным профит-фактором. Считается, что минимальное допустимое значение для достоверного профит-фактора 1,6.

Что меня всегда смущало в профит-факторе, так это то, что никак не учитывается динамика рынка и интенсивность торговли. Поэтому я предлагаю другой подход к оценке значимости профит-фактора, нежели сравнение с каким-то заданным априори значением: профит-фактор должен быть как можно выше, но не ниже, чем профит-фактор случайной системы на случайном рынке с аналогичной интенсивностью торговли и волатильностью соответственно (по сути, не ниже чем у «сферического трейдера» в «идеальном газе» или в «вакууме»).

Осталось только построить идеальную модель для сравнения.

«Сферический трейдер...»

Предположим, что мы рассматриваем некоторую случайную торговую систему («сферический трейдер»). Так как модель случайна, то торговые события наступают в случайные моменты времени, независимо от решений, принятых ранее. Направление сделок также случайно (с вероятностью 0,5 продажа либо покупка). Объём сделок предположим константой и без потери общности будем оценивать доход и убыток в пунктах.

Пусть средняя длительность сделки составляет , а среднее время между закрытием двух последующих сделок (не будем накладывать никаких ограничений на количество одновременно открытых сделок).

Также предположим, что мы будем иметь дело с Пуассоновыми потоками событий:

Длительность сделки будет являться случайной величиной с экспоненциальным распределением:

где .

Количество сделок , совершённых за период времени будет описываться распределением Пуассона:

где .

"… в вакууме"

Теперь рассмотрим идеальную среду обитания «сферического трейдера» — «вакуум», то есть полностью случайный рынок.

Предположим, что рынок описывается нормальным распределением изменения значений котировок за период времени :

где определяется следующим образом: пусть за единичное время котировки меняются на нормально распределённую случайную величину с дисперсией , тогда, если рассматривать интервалы времени , по изменения котировок будет иметь дисперсию:

Это известное соотношение для Броуновского процесса.

С учётом формул (2.1) и (1.1) результат сделки, рассматриваемый как изменение котировок за период времени с начала до конца сделки будет описываться как интеграл условной вероятности по :

или

Решение этого интеграла с использованием Wolfram Mathematica даёт следующий результат:

или

где .

Полученная закономерность является распределением Лапласа.

Таким образом, доход или убыток по одной сделке случайной системы на случайном рынке описывается распределением Лапласа, а абсолютная величина результата сделки имеет экспоненциальное распределение:

где .

Известно, что экспоненциальное распределение является частным случаем распределения хи-квадрат ( при ). Это значит, что суммарный доход и суммарные потери могут описываться как суммы случайных величин с распределением хи-квадрат, а значит сами являются хи-квадрат величинами.

Пусть было совершено прибыльных сделок с результами и убыточных с абсолютными значениями потерь . Тогда суммарный доход (нормированный на ) и суммарные потери (также нормированные на ) будут описываться распределениями хи-квадрат со степенями свободы и соответственно:

где и .

отношение этих величин будет выглядеть следующим образом:

где суммарный доход, а суммарные потери. Их отношение — профит-фактор.

Теперь рассмотрим следующую величину:

Эту величину можно интерпретировать как «нормированный профит-фактор»: отношение среднего дохода к среднему убытку за сделку. Посмотрим, какое распределение имеет эта величина:

Полученная величина, отношение хи-квадрат величин, нормированных на количества их степеней свободы, — имеет распределение Фишера.

Таким образом, мы нашли распределение величины, статистики для профит-фактора «сферического трейдера в вакууме» при известном количестве прибыльных и убыточных сделок.

Прежде чем переходить к обобщению на случай неизвестных и , рассмотрим поведение «сферического трейдера» на «не совсем случайном» рынке (назовём эту среду в шутку «идеальным газом»).

"… в идеальном газе"

Теперь рассмотрим чуть более сложную ситуацию: когда рынок является обобщённым броуновским движением. То есть, в отличие от случайного, обладает памятью. В этом случае формула (2.2) примет следующий вид:

где — показатель Хёрста, величина, характеризующая фрактальные свойства временного ряда и связанная с фрактальной размерностью Хаусдорфа-Безиковича следующим образом: . Показатель Хёрста может принимать значения .

При временной ряд вырождается в случайный, не обладающий памятью, соответсвует рассмотренному выше случаю. При ряд постоянно стремится к изменению направления существующей тенденции, а значит обладает памятью, такой ряд называется антиперсистентным, хаотическим. При ряд также обладает памятью, но стремится к сохранению существующей тенденции, такой ряд называется персистентным, детерминированным. Чем сильнее показатель Хёрста отличен от 0.5, тем чётче у ряда выражены хаотические или детерминированные свойства.

Для различных рынков характерны различные значения показателя Хёрста, кроме того, они могут меняться со времен. Показатель Хёрста может быть рассчитан по значениям временного ряда. А значит, при оценке профит-фактора можно учесть величину , рассчитанную по ряду котировок в тот же период, когда совершались сделки анализируемой стратегии. Для оценки показателя Хёрста существует несколько стандартных процедур, например RS-статистика или методы основанные на вейвлетах.

Предположим, что случайная торговая стратегия работает на рынке с показателем Хёрста H, тогда с учётом (3.1), формула (2.3) примет вид:

Очевидно, что при это выражение эквивалентно (2.3).

К сожалению, выражение (3.2) в аналитическом виде не интегрируется. Поэтому, для нахождения распределения абсолютных значений разностей котировок между моментами времени начала и конца сделки (абсолютных итогов сделок) при случайной торговле на рынке с показателем Хёрста мы воспользуемся численным моделированием.

Я проводил моделирование с использованием Python.

Моделирование проводится следующим образом

1) Задаём параметры моделирования:
— объём экспериментальной выборки;
— количество диапазонов для построения гистограммы

2) Генерируем выборку distE экспоненциально распределённой случайной величины и выборку distN нормально распределённой величины объёмом N каждая.

3) Учитывая соотношение (3.1), создаём тестовую выборку distT, каждое значение которой рассчитывается из соответствующих значений distN и distE:

4) Для полученного распределения строится гистограмма из M диапазонов (количество попаданий в диапазоны). Из полученной гистограммы выбирается K первых диапазонов, количество попаданий в которые отлично от нуля. Также производится нормирование на количество попаданий в первый диапазон.

5) На основании полученной гистограммы аппроксимируется вид распределения.

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

def testH(N, M, H, p):
    distE = np.random.exponential(1, N)
    distN = np.random.normal(0, 1, N)
    
    distT = abs(distN * distE**H)
    
    if p == 1:
        plt.figure(1)
        plt.hist(distT, M)
        plt.title('H='+str(H))
    
    [y, x] = np.histogram(distT, M)
    
    K = 0;
    for i in range(M):
        if y[i] > 0:
            K = i
        else:
            break  
    
    y = y * 1.0 / y[0]
    x = x[1:K]
    y = y[1:K]
    
    return getCoeff(x, y, p, 'H='+str(H))

Примеры гистограмм полученных распределений для значений показателя Хёрста 0.1, 0.3, 0.5, 0.7 и 0.9 приведены ниже.

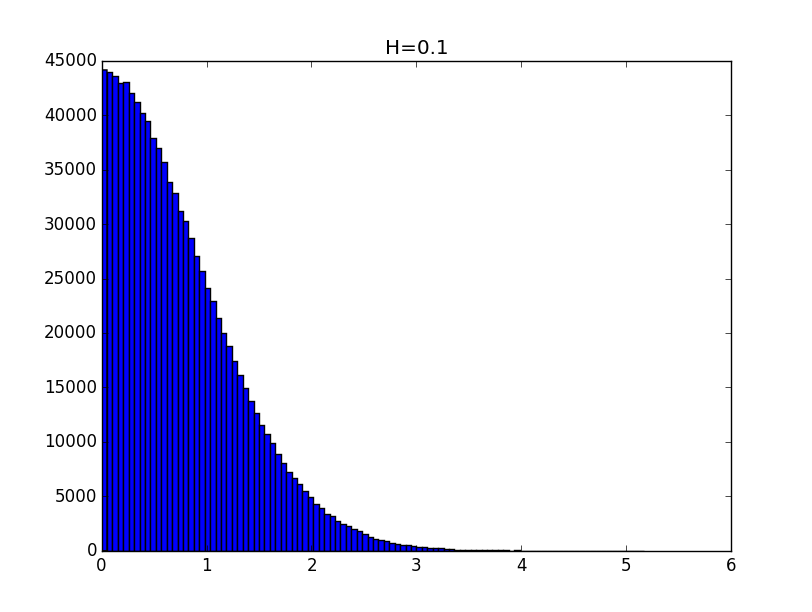
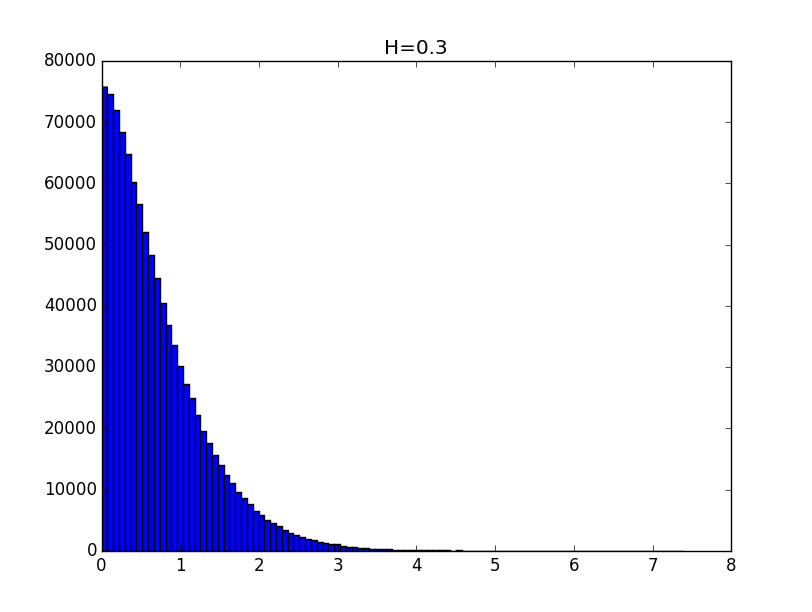
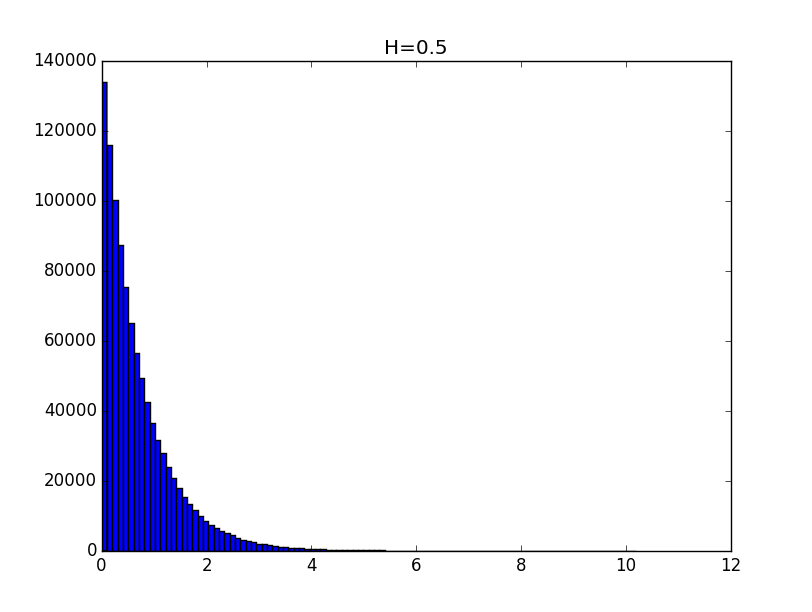
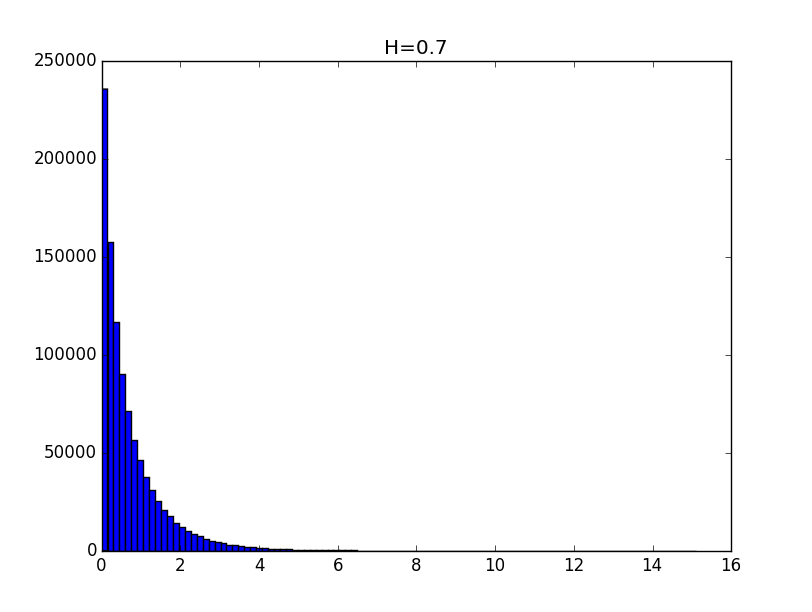
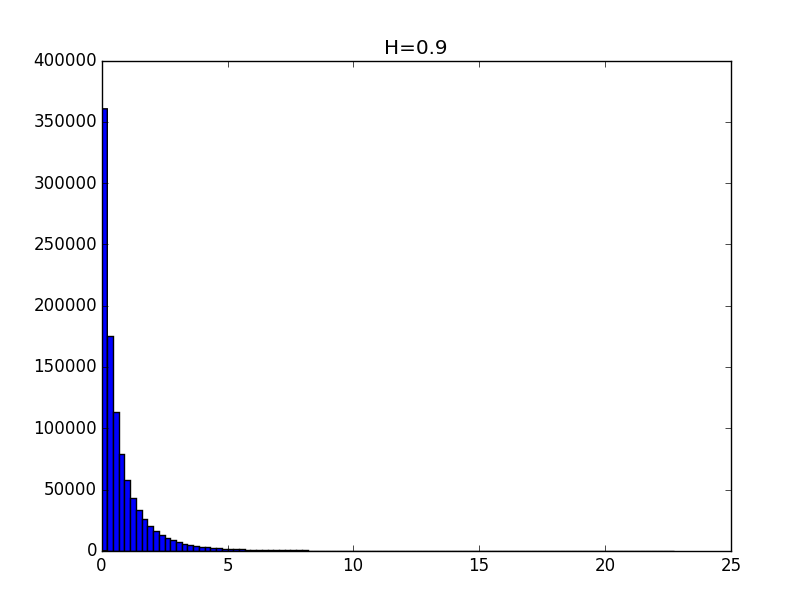
Общий вид гистограмм даёт основание предположить, что полученные распределения с точностью до константы могут описываться функцией вида:

Для поиска параметро распределения воспользуемся следующим алгоритмом:

1) Пусть нам даны — центроиды диапазонов гистограммы и — количества попаданий в диапазоны, нормированные на количество попадание в первый диапазон.

2) Тогда, игнорируя первый диапазон, выполним преобразования: и

3) Воспользовавшись методом наименьших квадратов, найдём параметры линейной регрессии и такие, что

4) На основании полученного принимаем:

.

Параметр компенсирует погрешность нормировки.

Листинг процедуры, выполняющей расчёт коэффициентов приведён ниже:

def getCoeff(x, y, p, S):
    X = np.log(x)
    Y = np.log(-np.log(y))
    n = len(X)
    
    k = (sum(X) * sum(Y) - n * sum(X * Y)) / (sum(X) ** 2 - n * sum(X ** 2))
    b = (sum(Y) - k * sum(X)) / n
    if p == 1:
        plt.figure(2)
        plt.plot(np.exp(X), np.exp(-np.exp(Y)), 'b', np.exp(X), np.exp(-np.exp(k * X + b)), 'r')
        plt.title(S)
        
        plt.show()
        
    return k

Ниже приводятся примеры для огибающих гистограмм для значений показателя Хёрста 0.1, 0.3, 0.5, 0.7 и 0.9 (синяя линия) и их модели (красная линия):

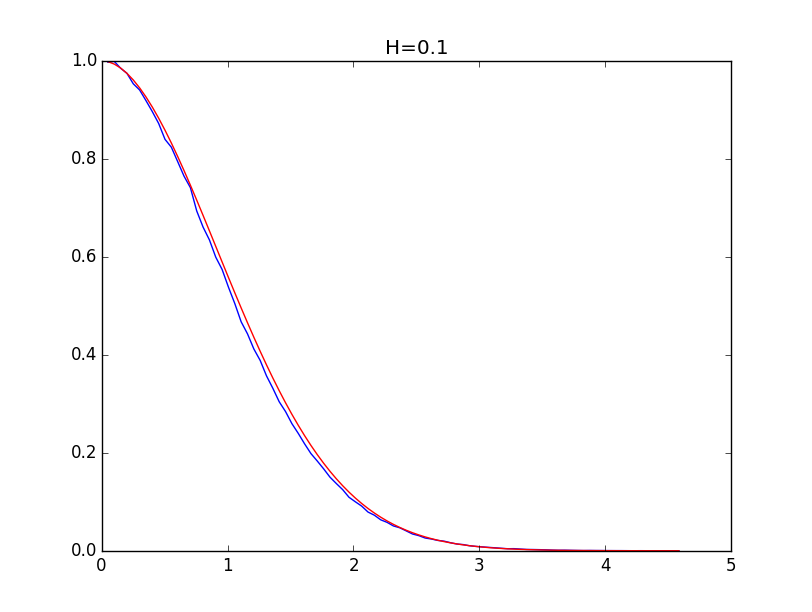
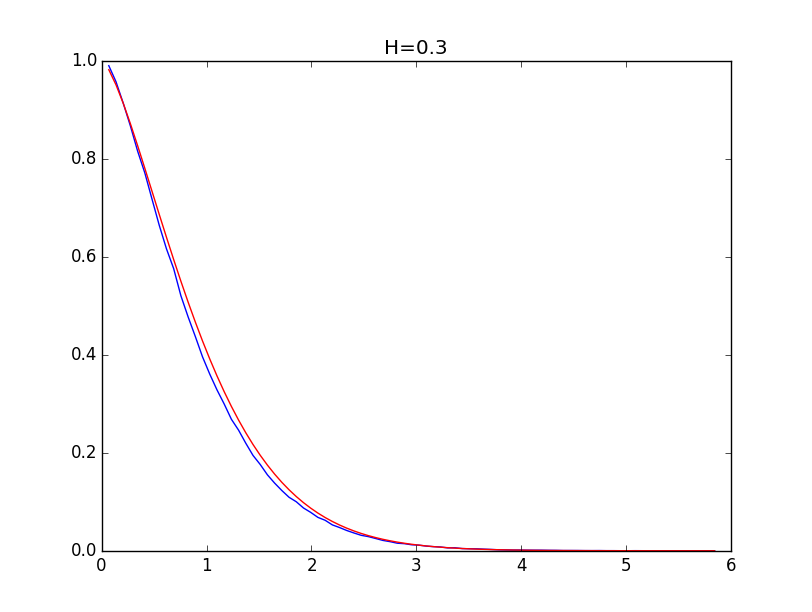
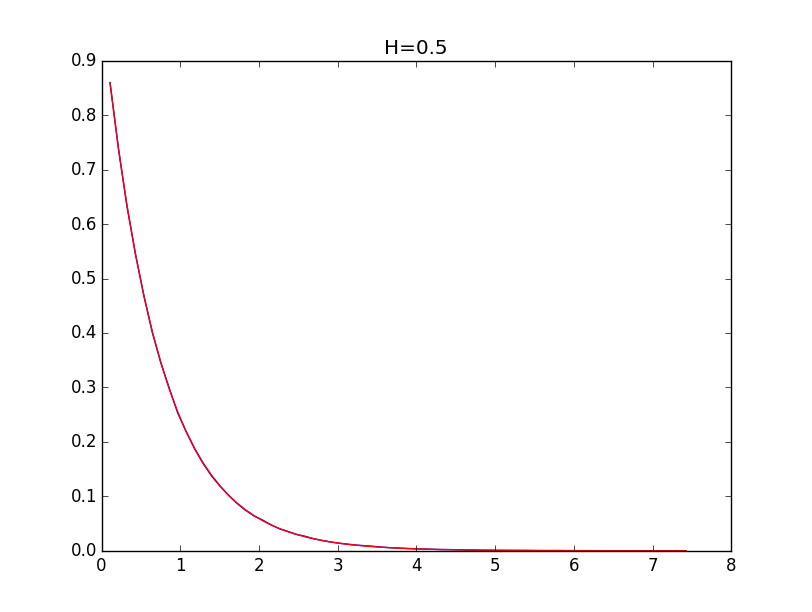
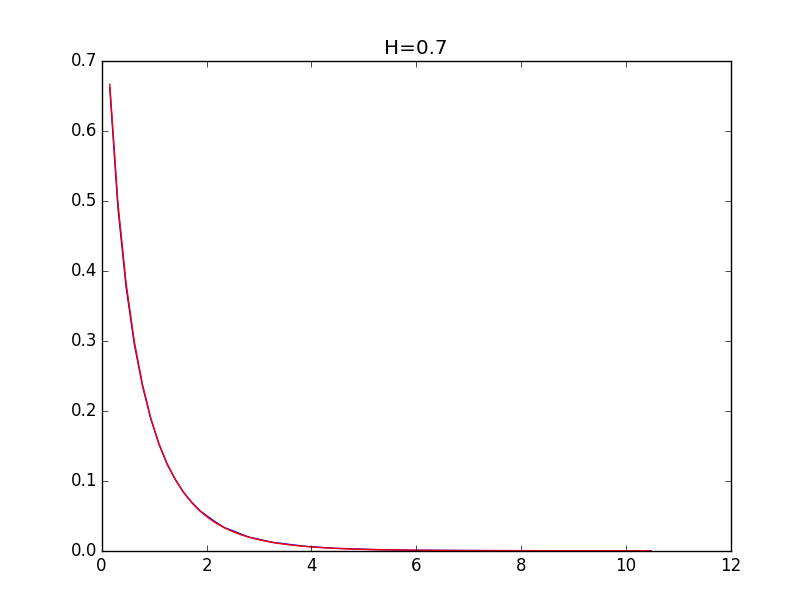
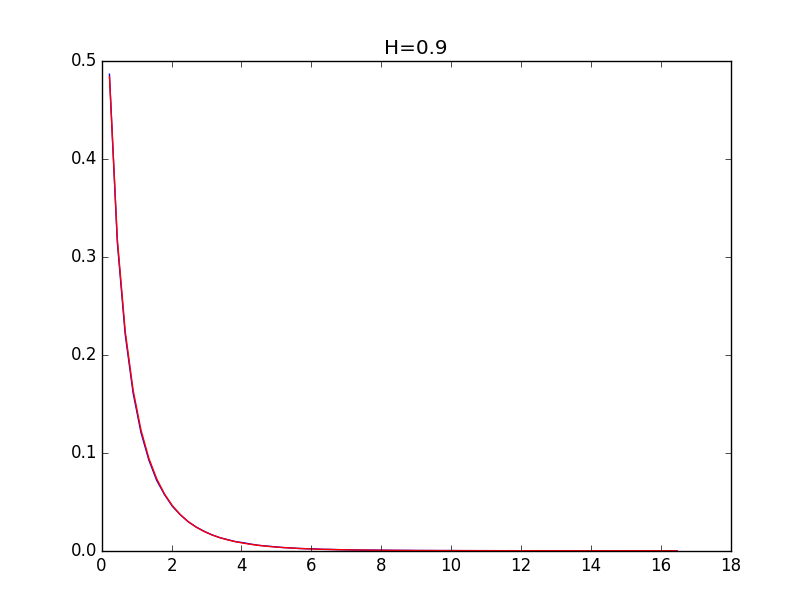
При значениях показателя Хёрста выше 0.5 точность моделирования выше.

Теперь найдём зависимость от . Для этого смоделируем ряд значений для различных и попробуем установить функциональную зависимость.

Я использовал для моделирования значения от 0.01 до 0.99 с шагом 0.01. При этом, для каждого значения значения вычислялись 20 раз и усреднялись:

if __name__ == "__main__":

    N = 1000000;  
    M = 100; 
    
    Z = np.zeros((99, 2))
    
    for i in range(99):
        Z[i, 0] = (i + 1) * 0.01
        
        for j in range(20):
            W = float('nan')
            while np.isnan(W):
                W = testH(N, M, (i + 1) * 0.01, 0)
            Z[i, 1] += W
            
        Z[i, 1] *= 0.05
        print Z[i, :]
                
    X = Z[:, 0].T
    Y = Z[:, 1].T

    plt.figure(1)
    plt.plot(X, Y)
     
    plt.show()

Полученная зависимость имеет следующий вид:

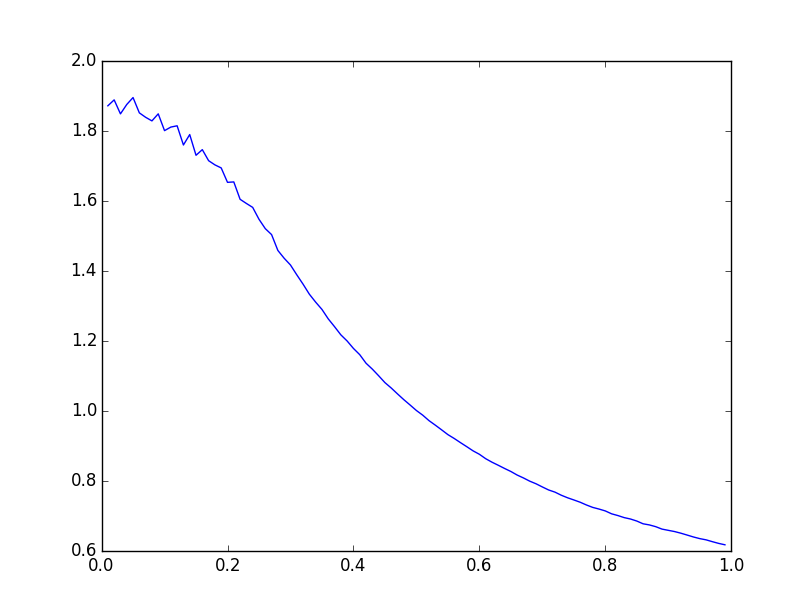
График похож на искажённый сигмоид, поэтому и закономерность будем искать в виде сигмоида:

Проведение численной процедуры минимизации методом наименьших квадратов даёт следующие результаты:

Суммарная квадратичная ошибка составляет порядка 0.005.

Ниже приведёны графики экспериментальной зависимости (синяя линия) и модельной по формуле (3.4) (красная линия):

Следует отметить, что полученная закономерность справедлива лишь для случая, когда и . Поэтому в дальнейшем будем полагать эти условия выполняющимися (обеспечим их выполнение) и опустим соответствующие индексы.

Теперь, учитывая (3.3) и (3.4) для оцененного значения мы знаем распределение абсолютного значения сделок. Используя свойство распределения преобразования случайной величины, произведём замену переменной в (3.4):

Тогда:

Это функция плотности вероятности величины, имеющей гамма-распределение с количеством степеней свободы и единичным параметром масштаба. Учитывая это, формула (3.6). Должна быть переписана как:

Подведём промежуточный итог:

Имея информацию о показателе Хёрста рынка , рассчитанном для того же периода истории, на котором мы тестируем систему, мы можем найти величину используя формулу (3.4). Также мы можем найти среднюю интенсивность торговли и параметр для результатов сделок. Для того, чтобы предложенные выше формулы были справедливы, необходимо привести значения и к единице. Для этого выполним нормировку: , где — результат сделки (независимо от знака результата). Это преобразование следует из (3.1).

Согласно (3.7), величины будут иметь гамма-распределения с параметрами . Следовательно, величины будут иметь распределение хи-квадрат c степенями свободы.

Пусть было совершено прибыльных сделок со значениями дохода и с величинами убытка (положительные значения). Тогда, с учётом и (3.7), величины

и

будут иметь хи-квадрат распределения с количествами степеней свободы и соответственно.

Следовательно, величина:

будет иметь распределение Фишера c степенями свободы (количество степеней свободы, в общем случае, будет нецелым, таким образом проявляются фрактальные свойства рынка).

Назовём величину обобщённым нормированным профит-фактором. При обобщённый профит-фактор вырождается в привычный нам нормированный профит-фактор (2.9).

Окончательное обобщение

Итак, мы исследовали «сферического трейдера» на случайном рынке и нашли распределение нормированного профит-фактора. Затем обобщили результаты на случай рынка с произвольной фрактальной размерностью, представленной измеримой величиной — показателем Хёрста.

Теперь у нас есть величина, которую мы назвали обобщённым нормированным профит-фактором, который вычисляется с использованием информации о результатах сделок (не забудем, кстати, скорректировать их с учётом спреда: отнять его от убытков и прибавить к доходам). Для большей универсальности методики, объём сделок считаем постоянным, либо измеряем всё в пунктах. Не забываем также проводить нормировку на среднюю длительность сделки и стандартное отклонение распределения результатов сделок: , где — результат сделки.

Все полученные на данный момент результаты завязаны на известное количество прибыльных и убыточных сделок, которое является случайной величиной с биномиальным распределением для известного общего количества сделок, которое, в свою очередь, также случайная величина, распределённая по Пуассону.

Введем новое обозначение. Пусть обобщённый нормированный профит-фактор (3.8) для заданного количества прибыльных и количества убыточных сделок (при известном показателе Хёрста ) обозначается как и имеет распределение Фишера со степенями свободы .

Тогда, с учётом биномиального распределения количества прибыльных и убыточных сделок, а также равновероятности получения дохода либо убытка на каждой сделке введём величину — обобщённый нормированный профит-фактор, учитывающий лишь общее количество сделок. Эта величина будет иметь следующее распределение:

где — плотность распределения Фишера со степенями свободы и , а величина описывается формулой (3.4), где — показатель Хёрста.

На практике, при достаточно больших выражение (4.1) может быть аппроксимировано неполной суммой:

где и () ограничивают некоторое подмножество возможных значений количества прибыльных сделок.

Теперь рассмотрим обобщённый нормированный профит-фактор без привязки к какому-либо количеству сделок, а лишь учитывающий среднюю интенсивность торговли и период тестирования стратегии : . Учитывая, что общее количество сделок распределено по Пуассону, будет иметь следующее распределение:

Или, для рассматриваемого количества сделок в диапазоне :

Полученное распределение может использоваться для проверки значимости рассчитанного по (3.8) обобщённого нормированного профит-фактора для торговой системы с известными средней длительностью сделки и интенивностью торговли за известное время работы на рынке с известными волатильностью и показателем Хёрста. Методика применения теста абсолютно аналогична таковой для теста Фишера. Для её проведения достаточно заменить в (4.1) (или в (4.1*)) функцию плотности на функию распределения Фишера и подставить в качестве аргумента значение рассчитанного обобщённого профит-фактора. Полученное значение вероятности необходимо сравнить с величиной , где — требуемый уровень значимости. При превышении этого уровня для рассчитанной статистики можно отвергать гипотезу о случайности торговой ситемы (о «сферичности трейдера в вакууме»).

Заключение

Предложенный в работе подход, основанный на построении обобщённого нормированного профит-фактора с учётом волатильности и фрактальных свойств рынка, а также интенсивности торговли и средней длительности сделок, позволяет построить статистический тест значимости достигнутых результатов с точки зрения вероятности получения аналогичных результатов случайным образом. Используя тест, можно с заданным уровнем значимости говорить о выполнении необходимого условия для констатации надёжности системы. Но полученные результаты не будут являться достаточным условием…

К сожалению, мне не известен тест, результатов которого будет достаточно для однозначного принятия стратегии как безусловно надёжной.

Автор: JamaGava

Источник