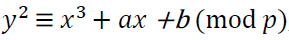ЭЦП стран СНГ на Python

в 7:03, , рубрики: Belt-hash, open source, python, Блог компании Virgil Security, Inc., ГОСТ 34.10-2012, ДСТУ 4145 – 2002, информационная безопасность, криптография, СТБ 34.101.45-2013, эллиптические кривые, эцп, метки: , , , , ,

image
Привет!
Я уже писал на Хабре о своей реализации блочных шифров стран СНГ. Выдалась еще одна свободная неделька в результате чего к симметричным стандартам добавились алгоритмы электронной цифровой подписи: российский ГОСТ 34.10-2012, украинский ДСТУ 4145-2002 и белорусский СТБ 34.101.45-2013.
Все три алгоритма основаны на эллиптических кривых. Но реализация каждого из стандартов имеет свои тонкости, о которых я хочу кратко рассказать в этой статье.

ГОСТ 34.10-2012

Итак, начинаем с российского стандарта. Тут все достаточно просто, в тексте стандарта прописано все необходимое и приведены наглядные примеры. Алгоритм работает с группой точек эллиптической кривой(ЭК) над полем большого простого числа p. Не лишним будет напомнить, что ЭК над конечным простым полем – это набор точек, описывающихся уравнением Вейерштрассе:
ЭЦП стран СНГ на Python - 2
Соответственно при использовании алгоритма сперва необходимо определиться с параметрами ЭК, а именно выбрать числа a, b, n и базовую точку P, с порядком равным большому простому числу q. Это означает, что если умножать точку на числа меньшие, чем q, то каждый раз будут получаться совершенно различные точки.
После выбора параметров можно приступать к генерации пары секретный-публичный ключ.
Секретный ключ d – случайное большое число удовлетворяющее неравенству 0<d<q.
Публичный ключ – точка эллиптической кривой Q вычисляемая как Q = d*P.

Процесс формирования ЭЦП выполняется по следующему алгоритму:

  1. Вычислить хеш сообщения M: H=h(M);
  2. Вычислить целое число α, двоичным представлением которого является H;
  3. Определить e=α mod q, если e=0, задать e=1;
  4. Сгенерировать случайное число k, удовлетворяющее условию 0<k<q;
  5. Вычислить точку эллиптической кривой C=k*P;
  6. Определить r = xC mod q, где xC — x-координата точки C. Если r=0, то вернуться к шагу 4;
  7. Вычислить значение s = (rd+ke) mod q. Если s=0, то вернуться к шагу 4;
  8. Вернуть значение r||s в качестве цифровой подписи.

Для проверки подписи нужно выполнить следующие шаги:

  1. По полученной подписи восстановить числа r и s. Если не выполнены неравенства 0<r<q и 0<s<q, тогда вернуть «подпись не верна»;
  2. Вычислить хеш сообщения M: H=h(M);
  3. Вычислить целое число α, двоичным представлением которого является H;
  4. Определить e=α mod q, если e=0, задать e=1;
  5. Вычислить v = e-1 mod q;
  6. Вычислить значения z1 = s*v mod q и z2 = -r*v mod q;
  7. Вычислить точку эллиптической кривой C = z1*G + z2*Q;
  8. Определить R = xc mod q, где xc — x-координата точки C;
  9. Если R=r, то подпись верна. В противном случае подпись не принимается.

Для проверки алгоритма можно воспользоваться примерами из текста стандарта.

Пример использования ГОСТ:

def test_gost_sign():
        p = 57896044618658097711785492504343953926634992332820282019728792003956564821041
        a = 7
        b = 43308876546767276905765904595650931995942111794451039583252968842033849580414
        x = 2
        y = 4018974056539037503335449422937059775635739389905545080690979365213431566280
        q = 57896044618658097711785492504343953927082934583725450622380973592137631069619
        gost = DSGOST(p, a, b, q, x, y)
        key = 55441196065363246126355624130324183196576709222340016572108097750006097525544
        message = 20798893674476452017134061561508270130637142515379653289952617252661468872421
        k = 53854137677348463731403841147996619241504003434302020712960838528893196233395
        sign = gost.sign(message, key, k)

def test_gost_verify():
        p = 57896044618658097711785492504343953926634992332820282019728792003956564821041
        a = 7
        b = 43308876546767276905765904595650931995942111794451039583252968842033849580414
        x = 2
        y = 4018974056539037503335449422937059775635739389905545080690979365213431566280
        q = 57896044618658097711785492504343953927082934583725450622380973592137631069619
        gost = DSGOST(p, a, b, q, x, y)
        message = 20798893674476452017134061561508270130637142515379653289952617252661468872421
        sign = (29700980915817952874371204983938256990422752107994319651632687982059210933395,
                    574973400270084654178925310019147038455227042649098563933718999175515839552)
        q_x = 57520216126176808443631405023338071176630104906313632182896741342206604859403
        q_y = 17614944419213781543809391949654080031942662045363639260709847859438286763994
        public_key = ECPoint(q_x, q_y, a, b, p)
        is_signed = gost.verify(message, sign, public_key)

Убеждаемся, что все результаты совпали с приведенными примерами и переходим к следующему стандарту.

СТБ 34.101.45-2013

Белорусский стандарт очень похож на ГОСТ. Эллиптическая кривая и базовая точка определяются параметрами a, b, n, P и q.
В качестве закрытого ключа используется число d. В то время как открытым ключом служит точка Q = d*P.

Для формирования подписи выполняются следующие шаги:

  1. Установить H ← ℎ(H).
  2. Выработать k ← {1, 2,..., q − 1}.
  3. Установить R ← kP.
  4. Установить S0 ← |belt-hash(OID(ℎ) ‖ |R|2l ‖ H)|l.
  5. Установить S1 ← |(k − H − (S0 + 2l)d) mod q|2l.
  6. Установить S ← S0 ‖ S1.
  7. Возвратить S.

Процедура проверки подписи выглядит так:

  1. Представить S в виде S = S0 ‖ S1, где S0 ∈ {0, 1}l, S1 ∈ {0, 1}2l.
  2. Если S1 > q, то возвратить НЕТ.
  3. Установить H ← ℎ(X).
  4. Установить R ← (︀(S1 + H) mod q)︀P + (S0 + 2l)Q.
  5. Если R = O, то возвратить НЕТ.
  6. Установить t ← |belt-hash(OID(ℎ) ‖ |R|2l ‖ H)|l.
  7. Если S0 != t, то возвратить НЕТ.
  8. Возвратить ДА.

Где l – уровень стойкости в битах (для схем на Эллиптических кривых этот показатель приблизительно равен половине длины ключа).
H – хеш-функция.
OID – идентификатор используемого алгоритма хеширования. При использовании belt-hash это значение всегда равно 0x 06092A7000020022651F51.
|R|l — первые l бит числа R.
|| — конкатенация двух битовых последовательностей.
Как видите в стандарте жестко прописано использование хеш-функции belt-hash, без которой нельзя будет проверить правильность реализованного алгоритма.
Благо в основе функции лежит стандарт блочного шифрования Республики Беларусь Belt, реализацию которого на Python можно найти тут. Допилив алгоритм хеширования можно приступать к реализации самой ЭЦП. Однако при этом следует учесть еще одну особенность стандарта СТБ 34.101.45-2013. Все числа в примерах приведены в little-endian нотации, и для того чтобы результаты сошлись с приведенными в стандарте необходимо перевести их к big-endian.

Проверив примеры из стандарта

def test_stb_sign():
        p = 0x43FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
        p = reverse(p)
        a = 0x40FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
        a = reverse(a)
        b = 0xF1039CD66B7D2EB253928B976950F54CBEFBD8E4AB3AC1D2EDA8F315156CCE77
        b = reverse(b)
        q = 0x07663D2699BF5A7EFC4DFB0DD68E5CD9FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
        q = reverse(q)
        y = 0x936A510418CF291E52F608C4663991785D83D651A3C9E45C9FD616FB3CFCF76B
        y = reverse(y)
        d = 0x1F66B5B84B7339674533F0329C74F21834281FED0732429E0C79235FC273E269
        d = reverse(d)
        stb = STB(p, a, b, q, y, 128)
        message = 0xB194BAC80A08F53B366D008E58
        k = 0x4C0E74B2CD5811AD21F23DE7E0FA742C3ED6EC483C461CE15C33A77AA308B7D2
        k = reverse(k)
        signature = stb.sign(message, d, k)

def test_stb_verify():
        p = 0x43FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
        p = reverse(p)
        a = 0x40FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
        a = reverse(a)
        b = 0xF1039CD66B7D2EB253928B976950F54CBEFBD8E4AB3AC1D2EDA8F315156CCE77
        b = reverse(b)
        q = 0x07663D2699BF5A7EFC4DFB0DD68E5CD9FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
        q = reverse(q)
        y = 0x936A510418CF291E52F608C4663991785D83D651A3C9E45C9FD616FB3CFCF76B
        y = reverse(y)
        message = 0xB194BAC80A08F53B366D008E584A5DE48504FA9D1BB6C7AC252E72C202FDCE0D5BE3D61217B96181FE6786AD716B890B
        q_x = 0xBD1A5650179D79E03FCEE49D4C2BD5DDF54CE46D0CF11E4FF87BF7A890857FD0
        q_x = reverse(q_x)
        q_y = 0x7AC6A60361E8C8173491686D461B2826190C2EDA5909054A9AB84D2AB9D99A90
        q_y = reverse(q_y)
        s = (0x47A63C8B9C936E94B5FAB3D9CBD78366, 0x290F3210E163EEC8DB4E921E8479D4138F112CC23E6DCE65EC5FF21DF4231C28)
        pub_key = (q_x, q_y)
        stb = STB(p, a, b, q, y, 128)
        is_signed = stb.verify(message, pub_key, s)

переходим к ДСТУ 4145-2002.

ДСТУ 4145 – 2002

В отличие от двух предыдущих стандартов, ДСТУ 4145-2002 основан на эллиптических кривых над полями характеристики 2. Это означает, что для них работает совсем другая математика. Основное отличие заключается в том, что арифметические действия выполняются не над числами, а над многочленами. В стандарте приводится два варианта реализации математических операции: в полиномиальном базисе и в оптимальном нормальном базисе. Я реализовал первый вариант.
Алгоритм задается следующими параметрами:
A, B – коэффициенты уравнения ЭК 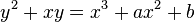image
k, m – количество членов и старшая степень основного многочлена, по модулю которого выполняются все арифметические операции. К примеру, k=5, m=5 задает следующий многочлен: x^5+x^3+x^2+x+1.
P – Базовая точка порядка n.
Пара ключей состоит из секретного ключа d и публичного ключа Q = -d*P.

Процедура формирования подписи следующая:

  1. Генерируем число e, такое что 1<e<n.
  2. Вычисляем точку R = e * P.
  3. Вычисляем многочлен f_r = R_x * h(M), где R_x – x-координата точки R; h(M) – хеш от подписываемого сообщения M.
  4. Представляем f_r как число r.
  5. Вычисляем число s = (e + d * r) mod n.
  6. Возвращаем пару (r, s) в качестве подписи.

Для проверки подписи:

  1. Представляем подпись как пару числе (r, s).
  2. Вычисляем точку ЭК R = s * P + r * Q.
  3. Вычисляем элемент основного поля f_r = h(M) * R_x.
  4. Представляем f_r как число r1.
  5. Если выполняется равенство r1 = r, подпись верна

Запускаем тестовые примеры

def test_dstu_sign():
        dstu_x = 0x72D867F93A93AC27DF9FF01AFFE74885C8C540420
        dstu_y = 0x0224A9C3947852B97C5599D5F4AB81122ADC3FD9B
        dstu_a = 0x1
        dstu_b = 0x5FF6108462A2DC8210AB403925E638A19C1455D21
        dstu_p = 0x800000000000000000000000000000000000000c9
        dstu_n = 0x400000000000000000002BEC12BE2262D39BCF14D
        dstu = DSTU4145(dstu_p, dstu_a, dstu_b, dstu_x, dstu_y, dstu_n)
        message = 0x03A2EB95B7180166DDF73532EEB76EDAEF52247FF
        dstu_d = 0x183F60FDF7951FF47D67193F8D073790C1C9B5A3E
        dstu_e = 0x1025E40BD97DB012B7A1D79DE8E12932D247F61C6
        signature = dstu.sign(message, dstu_d, dstu_e)

def test_dstu_verify():
        dstu_x = 0x72D867F93A93AC27DF9FF01AFFE74885C8C540420
        dstu_y = 0x0224A9C3947852B97C5599D5F4AB81122ADC3FD9B
        dstu_a = 0x1
        dstu_b = 0x5FF6108462A2DC8210AB403925E638A19C1455D21
        dstu_p = 0x800000000000000000000000000000000000000c9
        dstu_n = 0x400000000000000000002BEC12BE2262D39BCF14D
        dstu = DSTU4145(dstu_p, dstu_a, dstu_b, dstu_x, dstu_y, dstu_n)
        message = 0x03A2EB95B7180166DDF73532EEB76EDAEF52247FF
        dstu_d = 0x183F60FDF7951FF47D67193F8D073790C1C9B5A3E
        dstu_Q = dstu.gen_keys(dstu_d)[1]
        signature = (0x274EA2C0CAA014A0D80A424F59ADE7A93068D08A7, 0x2100D86957331832B8E8C230F5BD6A332B3615ACA)
        is_signed = dstu.verify(message, signature, dstu_Q)

и получаем ожидаемые результаты.

P.S.

Ах да, исходники. Исходные коды на Python всех вышеописанных алгоритмов вы можете найти на GitHub.

Ссылки

  1. Текст стандарта ГОСТ 34.10-2012.
  2. Текст стандарта СТБ 34.101.45-2013.
  3. Текст стандарта ДСТУ 4145 – 2002(на украинском языке, содержит ошибку в формулах, описывающих сложение точек ЭК).

Автор: Virgil Security, Inc.

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js