
Занимаясь изучением алгоритмов обнаружения событий электрокардиограммы для исследовательской части дипломной работы, я обнаружил, что длительность R-R интервала кардиограммы, вычисленная даже с точностью до второго знака после запятой, достаточно точно характеризует сердечнососудистую систему конкретного человека. Поскольку я уже довольно давно увлекаюсь фрактальной геометрией, в моей голове моментально родилась мысль, как можно придать «личные» качеств какому-нибудь простейшему фрактальному объекту.
Так появилось «Электрокардиографическое дерево Пифагора».
Теоретическая часть – 1. Об электрокардиограмме
Графическая запись разности потенциалов, создающихся между различными участками сердечной мышцы в процессе ее возбуждения, называется электрокардиограммой (ЭКГ). Ориентация и величина этих потенциалов сердца на электрокардиограмме выражаются в амплитуде зубцов и их направленности (полярности) по отношению к изоэлектрической линии. И охватывают диапазон 0,15…300 Гц при уровне сигналов 0,3…3 мВ.
Нормальная ЭКГ состоит из зубцов и горизонтально расположенных между ними отрезков (сегментов) линий (Рисунок 1).
Рисунок 1 – Схематическое изображение нормальной электрокардиограммы.
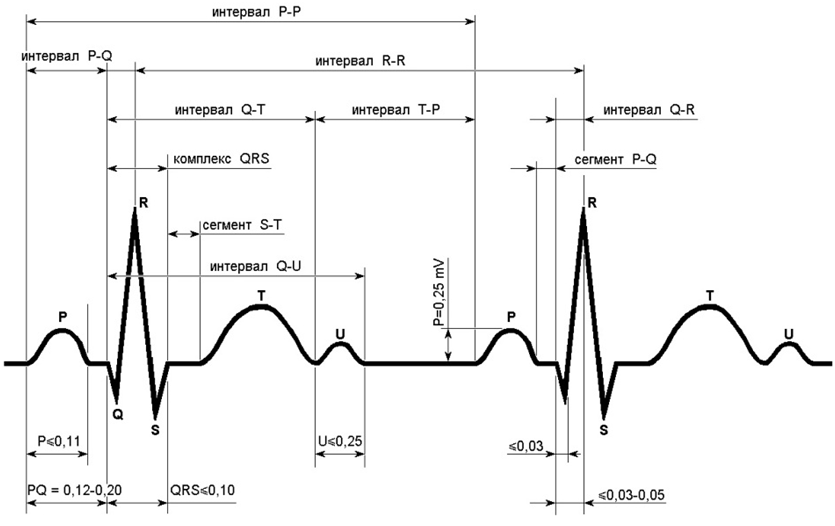
В клинической практике применяются отведения от различных участков поверхности тела. Эти отведения называются поверхностными. При регистрации ЭКГ обычно используется 12 общепринятых отведений, шесть от конечностей и шесть грудных. Первые три стандартных отведения были предложены Эйнтховеном. Частота сокращений сердца (ЧСС) определяется по продолжительности одного сердечного цикла, т.е. по продолжительности интервала R – R.
Стандартным и наиболее удобным для определения ЧСС является II-отведение по Эйнтховену, т.к. в нем наибольшую амплитуду имеет именно зубец R.
Практическая часть – 1
Для расчетов будем использовать реальную ЭКГ здорового человека во II-отведении по Эйнтховену, полученную из базы данных физиологических сигналов [1].
Параметры ЭКГ:
• Разрешение АЦП 12 бит;
• Частота семплирования 100 Гц;
• Длительность 10 секунд;
Рисунок 2 – Изображение нормальной ЭКГ из БД.
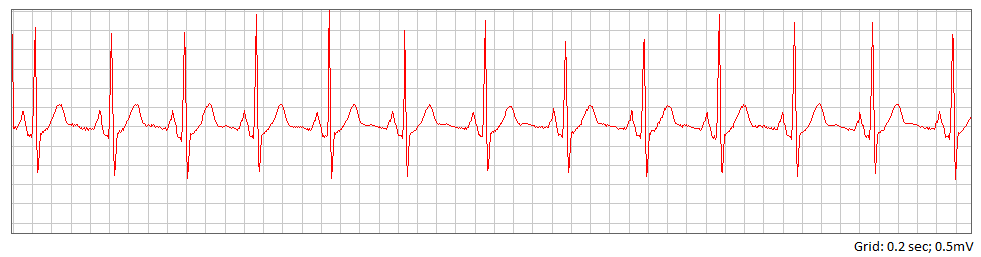
Далее определим QRS-комплекс, чтобы потом из него выделить зубец R. Для этого воспользуемся алгоритмом, основанном на взвешенном и возведенном в квадрат операторе первой производной и на фильтре скользящего среднего [2].
Звучит сложнее, чем выглядит:
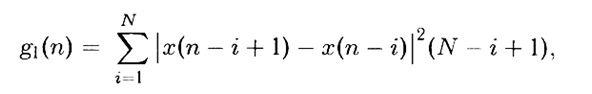
где x(n) — сигнал ЭКГ, N-ширина окна, в пределах которого разность первого порядка вычисляется, возводится в квадрат и взвешивается с использованием, коэффициента (N-i+1).
Взвешивающий коэффициент линейно спадает, начиная от текущей разности, до разности вычисленной на N отсчетов ранее по времени, что обеспечивает сглаживающий эффект.
Дальнейшее сглаживание выполняется с использованием фильтра скользящего среднего по M точкам:
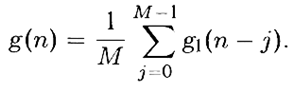
При частоте дискретизации 100Гц ширина окна фильтра устанавливается как M=N=8. Данный алгоритм дает единственный пик для каждого QRS-комплекса и подавляет зубцы P и Т. В результате обработки, получаем следующий вид ЭКГ (Рисунок 3).
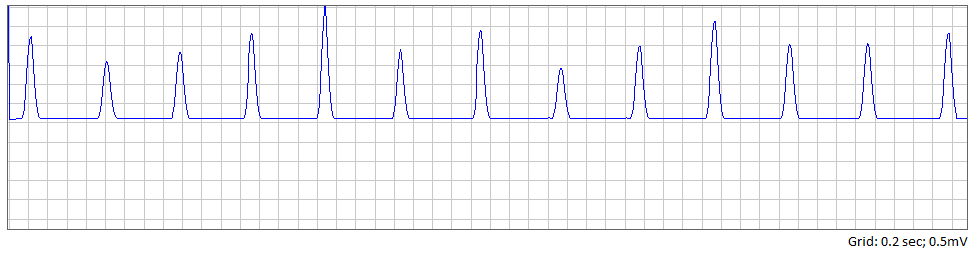
Рисунок 3 – Изображение ЭКГ после фильтрации.
Поиск зубца R в обработанном сигнале может быть выполнен с помощью простого алгоритма поиска пиков:
1. Сканирование фрагмента сигнала g(n), на котором ожидается наличие пика, и определение максимальной величины gmax.
2. Определение порога, как некоторой доли от максимума, Th=0.8gmax.
3. Для всех g(n)>Th выбираются те отсчеты, для которых соответствующие величины g(n) больше, чем определенное заданное число M предыдущих или последующих отсчетов g(n).
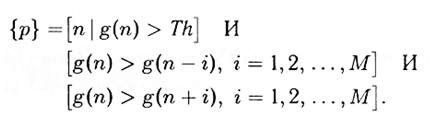
Определенный таким образом набор {p} содержит индексы всех найденных в сигнале g(n) пиков.
Пики, вызванные артефактами, можно отбраковать дополнительными условиями, например — минимальный интервал между двумя соседними пиками.
Рисунок 4 – Изображение ЭКГ с отмеченными R-зубцами.
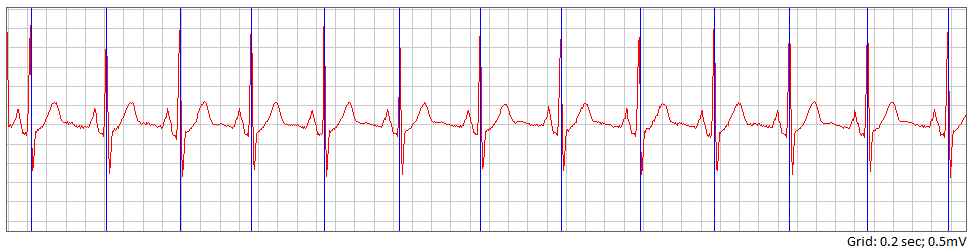
Далее стоит сама простая задача — определение средней длины R-R интервала данной ЭКГ. И в этом случае она равна 953мс. «По фану» рассчитаем ЧСС (пульс): 0.953*6*13=74,334 ударов/мин. Теперь у нас есть величина, характеризующая работу сердца конкретного человека.
Небольшое пояснение:
Сердце – не метроном, оно не может выстукивать такт с равными временными промежутками между ударами. R-R интервал для здорового человека колеблется в небольших пределах. Если колебания интервала будут значительными – это свидетельствует о наличии аритмий и других нарушений. Механизм колебаний является очень сложным комплексом процессов, связанным с электрической проводимостью конкретного сердца.
Используя величину среднего R-R интервала в качестве параметра при построении дерева Пифагора можно придать ему «неповторимые» («личные») черты.
Теоретическая часть – 2. О фракталах
Фракталами называются геометрические объекты: линии, поверхности, пространственные тела, имеющие сильно изрезанную форму и обладающие свойством самоподобия. Основоположник теории фракталов франко-американский математик Бенуа Мандельброт образовал термин фрактал от латинского причастия fractus. Соответствующий глагол frangere переводится, как ломать, разламывать, т.е. создавать фрагменты неправильной формы. Самоподобие, предопределяет масштабную инвариантность (скейлинг) основных геометрических особенностей фрактального объекта, их неизменность при изменении масштаба. Повторяемость изрезанности линий фрактальных объектов может быть полной (в этом случае говорят о регулярных фракталах), либо может наблюдаться некоторый элемент случайности (такие фракталы называют случайными). Структура случайных фракталов на малых масштабах не является точно идентичной всему объекту, но их статистические характеристики совпадают.
Дерево Пифагора — разновидность геометрического регулярного фрактала, основанная на фигуре, известной как «Пифагоровы штаны» [3].
Принцип построения геометрического фрактала — рекурсия.
Практическая часть – 2
Алгоритм построения дерева Пифагора:
1) Строим вертикальный отрезок;
2) Из верхнего конца этого отрезка рекурсивно строим еще 2 отрезка меньшей длины под углом 90° друг к другу;
3) Вызываем функцию построения двух последующих отрезков для каждой ветви дерева;
Функция построения дерева Пифагора на языке С.
void Draw(double x, double y, double L, double a) {
if(L > max) {
L*=0.7;
moveto(x,y);
lineto((int)(x+L*cos(a)),(int)(y-L*sin(a)));
x=x+L*cos(a);
y=y-L*sin(a);
Draw(x,y,L,a+Pi/n);
Draw(x,y,L,a-Pi/m);
}
}
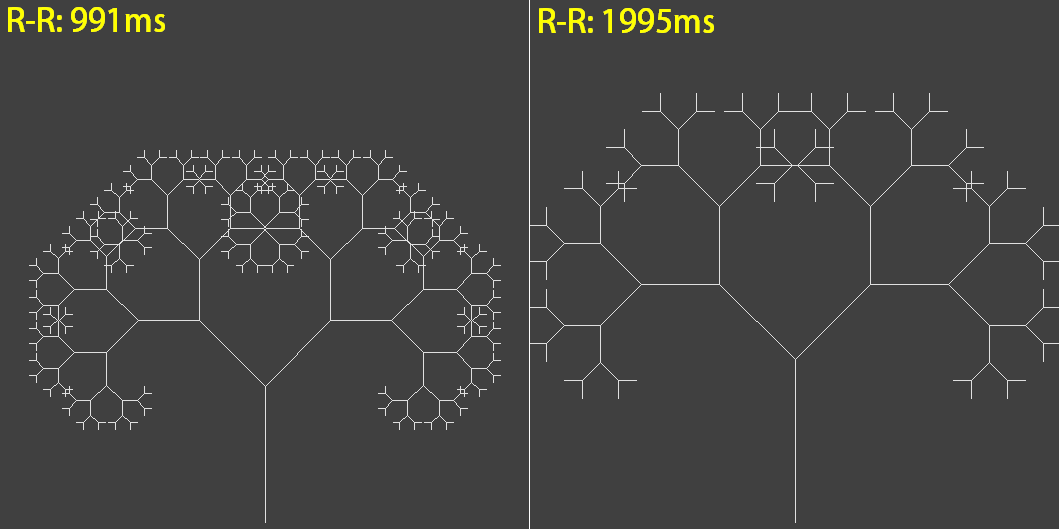
Рисунок 5 – дерево Пифагора для ЭКГ при R-R: 953ms.

Единственное, что осталось изменить — это в качестве переменной L использовать в программе вычисленную длину среднего R-R интервала ЭКГ.
Таким образом можно получить «личное» дерево Пифагора, которое будет «дышать», в зависимости от физической нагрузки, а длина ветвей и их закрученность — «максимально точно описывать» вашу личность.

Список литературы
1. Исследовательский ресурс сложных физиологических сигналов: physionet.org;
2. Рангайян Р.М. Анализ биомедицинских сигналов. Практический подход / Пер. с англ. Под ред. А.П. Немирко. – М.: Физматлит, 2010. – 220 с. – ISBN 978-5-9221-0730-3;
3. ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D0%9F%D0%B8%D1%84%D0%B0%D0%B3%D0%BE%D1%80%D0%B0
Автор: Jeffry_Choser
