
В предыдущих статьях (раз, два) мы рассматривали классический hash map с хеш-таблицей и списком коллизий. Был построен lock-free ordered list, который послужил нам основой для lock-free hash map.
К сожалению, списки характеризуются линейной сложностью поиска O(N), где N — число элементов в списке, так что наш алгоритм lock-free ordered list сам по себе представляет небольшой интерес при больших N.
Или все же представляет?..
Существует довольно любопытная структура данных — skip-list, основанная на обычном односвязном списке. Впервые она была описана в 1990 году W.Pugh, перевод его оригинальной статьи есть на хабре. Эта структура представляет для нас интерес, так как, имея алгоритм lock-free ordered list, довольно легко реализовать lock-free skip-list.
Для начала — немного о принципах построения skip-list. Skip-list представляет собой многоуровневый список: каждый элемент (иногда называемый башней, tower) имеет некоторую высоту h.
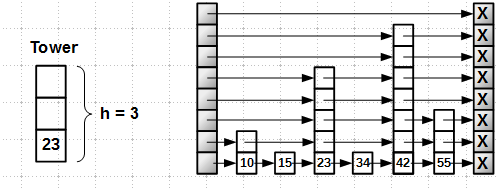
Высота h выбирается случайным образом из диапазона [1, Hmax], где Hmax — максимально возможная высота, обычно 16 или 32. Вероятность того, что высота башни равна единице, есть P[h == 1] = 1/2. Вероятность высоты k есть:
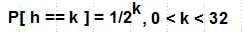
Несмотря на кажущуюся сложность вычисления высоты, её можно рассчитать довольно просто, например, так: h = lsb( rand() ), где lsb — номер младшего значащего бита числа.
1/2 — это мое упрощение, в оригинальной статье идет речь о 0 < p < 1 и исследуется поведение skip-list при различных значениях p. Но для практической реализации p = 1/2 — наилучшее значение, мне кажется.
Получается, что чем больше уровень, тем более список на этом уровне разрежен по сравнению с нижележащими. Эта разреженность наряду с вероятностной природой дает оценку сложности поиска O(log N), — такую же, как для бинарных самобалансирующихся деревьев.
Поиск в skip-list'е довольно прост: начиная с head-башни, которая имеет максимальную высоту, проходим по самому верхнему уровню, пока не найдем элемент с ключом больше искомого (или не упремся в хвост tail), спускаемся на уровень ниже, ищем аналогично в нем и т.д., пока не попадем на уровень 0, самый нижний; пример поиска ключа 34:
Lock-free skip list
Для построения lock-free skip-list у нас уже есть lock-free алгоритм для каждого уровня. Осталось разработать приемы работы с уровнями. Казалось бы, невозможно атомарно вставить узел-башню высотой, скажем, 20, — ведь для этого нужно атомарно поменять 20 указателей! Оказывается, этого и не нужно, достаточно уметь атомарно менять один указатель, — то, что мы уже умеем делать в lock-free list.
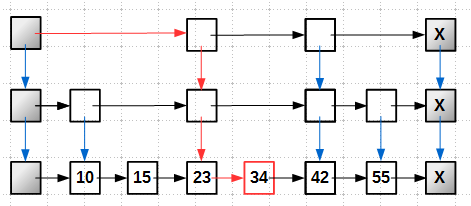
Рассмотрим, как происходит вставка в lock-free skip-list. Будем вставлять элемент-башню высотой 5 с ключом 23. Первым этапом мы ищем позицию вставки, двигаясь по уровням сверху вниз. В результате у нас получается массив prev[] позиций вставки на каждом уровне:

Далее, вставляем новый элемент на уровень 0, самый нижний. Вставку в lock-free список мы уже умеем делать:
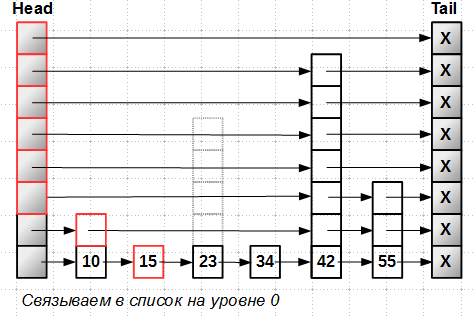
Всё, — элемент становится частью списка, его можно найти, он становится достижимым, несмотря на то, что вся башня целиком ещё не вставлена в skip-list.
Далее мы не торопясь вставляем нашу башню на уровни выше, снизу вверх:
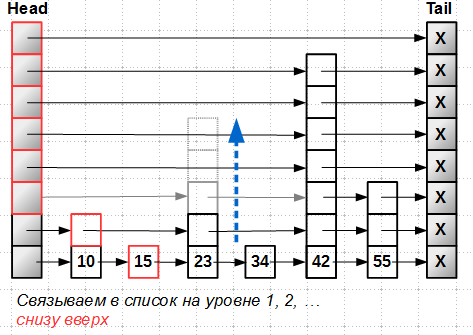
Эти вставки имеют уже второстепенное значение, призваны повысить эффективность поиска, но никак не влияют на принципиальную достижимость нового ключа.
Удаление элемента происходит в две фазы: сначала мы находим удаляемый элемент и помечаем его как логически удаленный, используя прием marked pointer. Сложность в том, что для башни мы должны пометить все уровни элемента, начиная с самого верхнего:
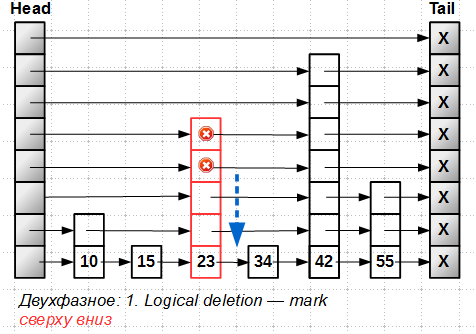
После того, как все уровни элемента-башни помечены, делается физическое удаление (точнее говоря, исключение элемента из списка, так как удаление памяти под элемент выполняется Hazard Pointer или RCU), также сверху вниз:

На каждом уровне применяется алгоритм вставки/удаления из обычного lock-free ordered list, который мы уже рассматривали.
Как видим, процедуры вставки/удаления из lock-free skip-list многошаговые, на каждом шаге возможна интерференция с конкурирующими операциями, поэтому при программировании skip-list нужна особая аккуратность. Например, при вставке мы сначала ищем позиции в списках на всех уровнях и формируем массивы prev[]. Вполне возможно, что в процессе вставки список на каком-то уровне изменится и эти позиции станут невалидными. В этом случае следует обновить prev[], то есть найти вставляемый элемент, и продолжить вставку, начиная с уровня, на котором произошел облом.
Более интересна ситуация, когда происходит одновременная вставка ключа K и его удаление. Такое вполне возможно: вставка считается успешно выполненной, когда мы связали элемент на уровне 0 списка. После этого элемент уже достижим и его вполне можно удалить, несмотря на то, что он ещё не до конца вставлен в верхние уровни. Для разрешения коллизии вставки и удаления очень важен порядок: вставка производится снизу вверх, а удаление (точнее, его первая фаза — логическое удаление, marked pointer) — противоходом, сверху вниз. В таком случае процедура вставки обязательно увидит на каком-либо уровне метку удаления и немедленно прекратит свою работу.
Процедура удаления также может быть конкурентной на обоих своих фазах. На фазе логического удаления, когда проставляются метки на башне сверху вниз, нам конкуренция не страшна. А вот на фазе исключения удаляемого элемента из списков любое изменение skip-list'а, то есть нарушение массивов prev[] и found[], определяющих позицию удаляемого элемента, приводит к тому, что нам надо эти массивы сформировать заново. Но метки уже проставлены и функция поиска просто не найдет удаляемый элемент! Для разрешения этой ситуации мы наделяем функцию поиска несвойственной ей работой: при обнаружении помеченного на каком-либо уровне элемента функция поиска исключает (unlink) этот элемент из списка этого уровня, то есть помогает удалять элементы. После исключения функция возобновляет поиск с самого начала, то есть с самого верхнего уровня (здесь возможны вариации, но самое простое — начать с начала). Это типичный пример взаимопомощи, часто встречающийся в lock-free программировании: один поток помогает другому делать его работу. Именно поэтому функция find() во многих lock-free контейнерах не является константной — поиск может изменить контейнер.
Чем ещё характеризуется skip-list? Во-первых, это упорядоченный map, в отличие от hash map, то есть поддерживает операции извлечения минимального extract_min() и максимального extract_max() ключей.
Во-вторых, skip-list прожорлив для схемы Hazard Pointrer (HP): при максимальной высоте башни 32 элементы массивов prev[] и found[], определяющих искомую позицию, должны быть защищены hazard pointer'ами, то есть нам требуется минимум 64 hazard pointer'а (на самом деле, в реализации libcds – 66). Это довольно много для схемы HP, см. подробнее её устройство. Для схемы RCU некоторую сложность представляет реализация метода find(), так как этот метод может удалять элементы, а схема RCU требует, чтобы удаление исключение (unlink) элемента из списка было под критической секцией RCU, а удаление деаллокация памяти — вне критической секции, иначе возможен deadlock.
Интересную практическую задачу представляет собой реализация башен для высоты более 1. Сейчас в реализации skip-list в библиотеке libcds память под башни высотой более 1 распределяется отдельно от памяти под элемент даже для интрузивного варианта. Учитывая вероятностную природу высоты, получается, что для 50% элементов делается распределение памяти, — это может сказаться на производительности, а также негативно влияет на фрагментацию памяти. Есть задумка башни высотой не более h_min распределять одним блоком и только для высоких «дораспределять» память под башню:
template <size_t Hmin = 4>
struct tower {
tower * next[Hmin];
tower * high_next; // массив для указателей уровней >= Hmin
};
Если Hmin = 4, то при таком построении 93% элементов не потребуют распределения дополнительной памяти под указатели next — high_next для них будет nullptr.

W.Pugh спустя год-два после опубликования своей работы о skip-list представил другую работу, посвященную конкурентной реализации, основанной на аккуратной расстановке блокировок (fine-grained locks).
Наиболее цитируемая работа по lock-free skip-list – это диссертация K.Fraser Practical lock-freedom 2003 года, в которой представлено несколько алгоритмов skip-list как на основе транзакционной памяти, так и на программной реализации MCAS (CAS над несколькими ячейками памяти). Эта работа представляет сейчас, на мой взгляд, чисто теоретический интерес, так как программная эмуляция транзакционной памяти довольно тяжела, равно как и MCAS. Хотя с выходом Haswell реализация транзакционной памяти в железе пошла в массы…
Реализация skip-list в libcds сделана по мотивам неоднократно цитируемой мною монографии The Art of Multiprocessor Programming. «По мотивам» потому, что оригинальный алгоритм приведен для Java и имеет, как мне кажется, несколько ошибок, которые, быть может, были исправлены во втором издании. Или это вовсе не ошибки для Java.
Есть ещё диссертация Фомичева, посвященная вопросу возобновления поиска в случае обнаруженных конфликтов в skip-list. Как я упоминал выше,
find() при обнаружении помеченного (marked) элемента пытается удалить его из списка и возобновляет поиcк с самого начала. Фомичев предлагает механизм расстановки back-reference – обратных ссылок, чтобы работу возобновлять с некоторого предыдущего элемента, а не с начала, что, в принципе, должно повлиять на производительность в лучшую сторону. Алгоритм поддержки back-reference в актуальном состоянии довольно сложный и непонятно, будет ли выигрыш или же его съест код поддержки актуальности.
В следующей статье попытаемся рассмотреть другой обширный класс структур данных, являющихся основой для ассоциативных контейнеров, — деревья, точнее, их конкурентную реализацию.
Автор: khizmax






