Разбор задачи «Зеркало в коридоре» и негодование

2015-02-16 в 19:44, admin, рубрики: математика, негодование, олимпиадные задачи, Программирование

Хочу более подробно разобрать задачу из публикации «Олимпиады по программированию среди школьников», а также показать, что она действительно нетривиальная. Хотя в результате программа и состоит из трех присваиваний и двух сравнений, прийти к этому результату не так уж и просто, тем более, если нет под рукой справочника по аналитической геометрии.

Разбор задачи «Зеркало в коридоре» и негодование - 1

Итак, сразу договоримся, что всяческих округлений и погрешностей, связанных с представлением чисел с плавающей точкой, у нас не будет. Работать будем исключительно с целочисленными переменными, для этого прибегнем к очевидным хитростям. Хотя, на самом деле, здесь будет мало программирования и много математики. В этой работе использованы справочные материалы по ВУЗовской математике, а точнее один параграф из главы «Основы линейной алгебры и аналитической геометрии» [1].

Для начала напомню текст задачи:

Простуженный Петя лежал в постели, как вдруг кто-то открыл дверь. Пете было лень вставать и он посмотрел в зеркало, чтобы увидеть кто пришёл. Известны координаты вошедшего (его можно считать материальной точкой), необходимо узнать, удасться ли Пете увидеть отражение вошедшего в зеркале. Зеркало имеет форму круга с центром в начале координат и расположено в плоскости ax + by + cz = 0. Петю тоже можно считать материальной точкой. Гарантируется, что Петя и незнакомец не лежат в плоскости зеркала и что Петя всегда видит отражающую сторону зеркала. Если изображение попадает на границу зеркала, то Петя видит вошедшего. Так как и Петю и вошедшего можно считать материальными точками, Петя может увидеть отражение вошедшего как сквозь вошедшего, так и сквозь свое собственное отражение.

Что ж, «в лоб» к этой задаче не подступиться, разбор в указанном топике тоже не особо что-то «разжевывает». Поэтому я предлагаю упростить задачу и решить ее для двумерного пространства, а потом по аналогии перейти уже к трехмерному.

Можно, конечно, рассмотреть даже и одномерный вариант, но смысла в нем мало, ибо зеркало превращается в точку и Петр увидит вошедшего только в том случае, когда они находятся по одну сторону от зеркала, т.е. если их координата имеет одинаковый знак.

Вычертим иллюстрацию к задаче:

Разбор задачи «Зеркало в коридоре» и негодование - 2

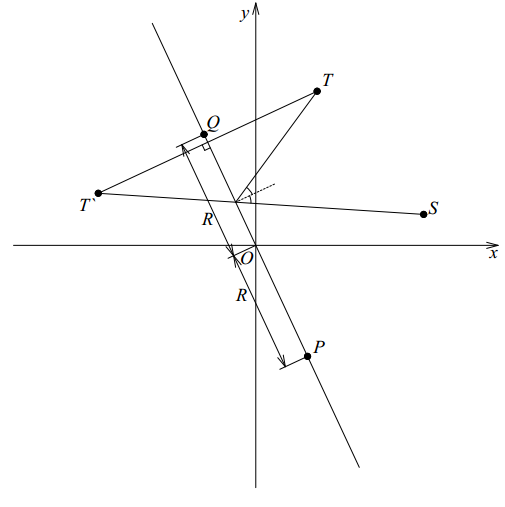
Обозначим Петю точкой S, незнакомца точкой T, зеркало — отрезок прямой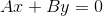
Исходные данные: R — радиус зеркала, коэффициенты A и B;
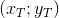— координаты вошедшего;
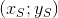— координаты Петра.

Алгоритм решения следующий:
— Через точку T проводим прямую, перпендикулярную PQ;
— На этой прямой отмечаем точку T` симметричную точке T относительно PQ — это будет изображение вошедшего, которое увидит (или не увидит) Петя;
— Проведем прямую ST`;
— Найдем точку пересечения PQ и ST`;
— Проверим, принадлежит ли данная точка отрезку PQ

Итак, уравнение прямой, проходящей через точку T перпендикулярно 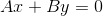выглядит следующим образом:
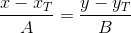или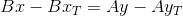

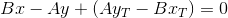
Точка пересечения TT` и PQ является решением системы уравнений:

Домножим уравнения на A и B соответственно и сложим между собой:

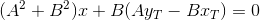
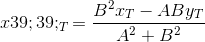
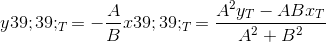
Найденная точка 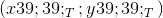— проекция точки T на прямую PQ
Определим координаты точки T`:

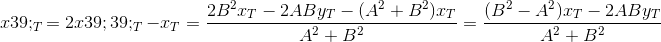
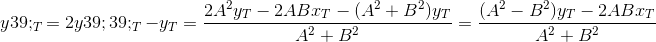
Два шага позади. Найдем уравнение прямой ST`:
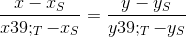или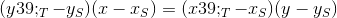
Подставим выражения для координат T`:

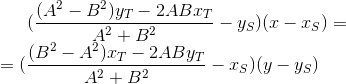
Уходим к целочисленному исчислению — умножаем уравнение на :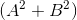

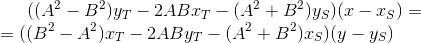
Самое время ввести замену:

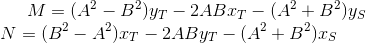
тогда уравнение ST` принимает вид:

Точка пересечения PQ и ST` является решением системы:

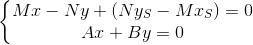
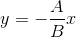
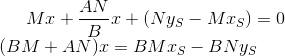
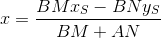
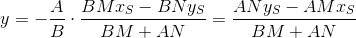
Ну и, наконец, расстояние от центра координат до найденной точки: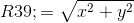
Уходим от радикалов: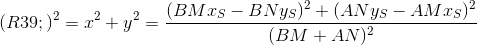
Теперь, если найденное R' будет не более заданного R, то наш несчастный Петр увидит все-таки вошедшего незнакомца.
В сравнении обе части неравенства умножим на заведомо положительное (т.к. четная степень)
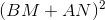
т.е. нас интересует истинность выражения

К чему я все это так подробно расписываю? Просто для того, чтобы показать какой объем работ должен проделать участник олимпиады для решения этой задачи, а ведь все эти формулы перпендикулярных прямых не входят в школьный курс математики, участник должен сам до них дойти логическим путем? При этом ему на эту задачу отведено в среднем 30 минут. Так ведь задача-то еще и не решена на самом-то деле. Во-первых надо все тоже самое проделать для трехмерного пространства, что еще более трудоемко, а во-вторых здесь не рассмотрено находятся ли мальчик и его гость по одну сторону от зеркала…

Чтож, нам-то цейтнот не грозит, поэтому продолжим.
Разберемся с «зазеркальем».
У меня такое решение (хотя оно тоже не сразу пришло в голову, сначала я думал о переходе к системе координат связанной с прямой зеркала, но там «некрасивые» тригонометрические функции) — через точки S и T проведем прямые параллельные заданной 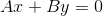. Параллельные прямые имеют кратные коэффициенты при x и y, т.е. 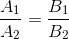, разница только в свободном члене. Мы ничего выдумывать не будем и возьмем эти коэффициенты равными заданным A и B.
Тогда уравнение прямой, проходящей через точку S параллельно PQ имеет вид: 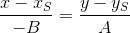или
Вот, в зависимости от знака свободного члена 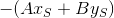прямая будет находиться с одной либо с другой стороны от заданной.
Аналогично для прямой, проходящей через T: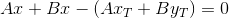

Сделаем следующее: найдем значение произведения 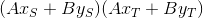и сравним его с нулем: если больше нуля — точки расположены по одну сторону от прямой, если меньше — по разные и Петя уже точно гостя своего не увидит, ну и промежуточный ноль — тоже удовлетворяет, т.к. в этом случае как минимум одна из точек лежит на заданной прямой.

Ну и напоследок приведу текст программы для трехмерного мира, т.е. для исходного условия задачи:

src

package ru.andrewn;

import static java.lang.System.out;

public class Program {

	public static void main(String[] args) {
		java.util.Scanner sc = new java.util.Scanner(System.in);
		
		out.println("Введите r:");
		int R = sc.nextInt();
		
		out.println("Введите a, b и c:");
		int A = sc.nextInt();
		int B = sc.nextInt();
		int C = sc.nextInt();
		
		out.println("Введите положение Петра (xп, yп и zп):");
		int xx = sc.nextInt();
		int yy = sc.nextInt();
		int zz = sc.nextInt();
		
		out.println("Введите положение входящего (x0, y0 и z0):");
		int x0 = sc.nextInt();
		int y0 = sc.nextInt();
		int z0 = sc.nextInt();
		
		if ( (A*x0+B*y0+C*z0)*(A*xx+B*yy+C*zz) >= 0 ) {
			int M = (B*B+C*C-A*A)*x0-2*A*B*y0-2*A*C*z0-(A*A+B*B+C*C)*xx;
			int N = (A*A+C*C-B*B)*y0-2*A*B*x0-2*B*C*z0-(A*A+B*B+C*C)*yy;
			int K = (A*A+B*B-C*C)*z0-2*A*C*x0-2*B*C*y0-(A*A+B*B+C*C)*zz;
			
			if ( (A*M+B*N+C*K)*(A*M+B*N+C*K)*R*R >=
					((B*N+C*K)*xx-B*M*yy-C*M*zz)*((B*N+C*K)*xx-B*M*yy-C*M*zz) +
					((A*M+C*K)*yy-A*N*xx-C*N*zz)*((A*M+C*K)*yy-A*N*xx-C*N*zz) +
					((A*M+B*N)*zz-A*K*xx-B*K*yy)*((A*M+B*N)*zz-A*K*xx-B*K*yy)) 
				out.println("Петр увидит входящего");
			else
				out.println("Петр не увидит входящего");
		}
		else
			out.println("Петр не увидит входящего");
		
		sc.close();
	}
}

Простите за кривизну кода, я далеко не программист.

Если будут желающие — могу приложить и математические выкладки для трехмерного мира.

Резюме

Мораль сей публикации в том, что составителям задач для олимпиад следует все же более тщательно проверять, на сколько трудоемко решение задачи и каких познаний оно требует для успешного выполнения в отведенное время.