Содержание курса
- Статья 1: алгоритм Брезенхэма
- Статья 2: растеризация треугольника + отсечение задних граней
- Статья 3: Удаление невидимых поверхностей: z-буфер
- Статья 4: Необходимая геометрия: фестиваль матриц
- 4а: Построение перспективного искажения
- 4б: двигаем камеру и что из этого следует
- Статья 5: Пишем шейдеры под нашу библиотеку
- Статья 6: Чуть больше, чем просто шейдер: просчёт теней
Сегодня мы заканчиваем с ликбезом по геометрии, в следующий раз будет веселье с шейдерами!
Чтобы не было совсем скучно, вот вам тонировка Гуро:

Я убрал текстуры, чтобы было виднее. Тонировка Гуро очень проста: добрый дяденька-моделёр дал нам нормальные вектора к каждой вершине объекта, они хранятся в строчках vn x y z файла .obj. Мы считаем интенсивность освещения для каждой вершины треугольника и просто интерполируем интенсивность внутри. Ровно как мы делали для глубины z или для текстурных координат uv!
Кстати, если бы дяденька-моделёр был не таким добрым, то мы могли бы посчитать нормали к вершине как среднее нормалей граней, прилегающих к этой вершине.
Текущий код, который сгенерировал эту картинку, находится здесь.
Ликбез: смена базиса в трёхмерном пространстве
В евклидовом пространстве система координат (репер) задаётся точкой отсчёта и базисом пространства. Что означает, что в репере (O, i,j,k) точка P имеет координаты (x,y,z)? Это означает, что вектор OP задаётся следующим образом:
Теперь представим, что у нас есть второй репер (O',i',j',k'). Как нам преобразовать координаты точки, данные в одном репере, в другой репер? Для начала заметим, что, так как (i,j,k) и (i',j',k') — это базисы, то существует невырожденная матрица М, такая что:
Давайте нарисуем иллюстрацию, чтобы было нагляднее:

Распишем представление вектора OP:
подставим во вторую часть выражение замены базиса:

И это нам даст формулу замены координат для двух базисов.
Пишем свой gluLookAt
OpenGL и, как следствие, наш маленький рендерер умеют рисовать сцены только с камерой, находящейся на оси z. Если нам нужно подвинуть камеру, ничего страшного, мы просто подвинем всю сцену, оставив камеру неподвижной.
Давайте поставим задачу следующим образом: мы хотим сделать так, чтобы камера находилась в точке e (eye), смотрела в точку c (center) и чтобы заданный вектор u (up) в нашей финальной картинке был бы вертикален.
Вот иллюстрация:
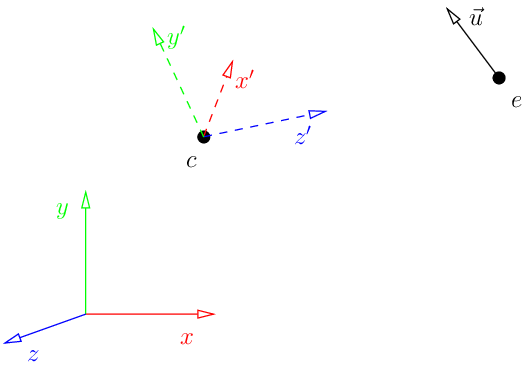
Это просто означает, мы делаем рендер в репере (c, x'y'z'). Но ведь модель задана в репере (O, xyz), значит, нам нужно посчитать репер x'y'z' и соответствующую матрицу перехода. Вот код, который возвращает нужную нам матрицу:
Matrix lookat(Vec3f eye, Vec3f center, Vec3f up) {
Vec3f z = (eye-center).normalize();
Vec3f x = (up^z).normalize();
Vec3f y = z^x;
Matrix res = Matrix::identity(4);
for (int i=0; i<3; i++) {
res[0][i] = x[i];
res[1][i] = y[i];
res[2][i] = z[i];
res[3][i] = center[i];
}
return res;
}
Начнём с того, что z' — это просто вектор ce (не забудем его нормализовать, так проще работать). Как посчитать x'? Просто векторным произведением между u и z'. Затем считаем y', который будет ортогонален уже посчитанным x' и z' (напоминаю, что по условию задачи вектор ce и u не обязательно ортогональны). Самым последним аккордом делаем параллельный перенос в c, и наша матрица пересчёта координат готова. Достаточно взять любую точку с координатами (x,y,z,1) в старом базисе, умножить её на эту матрицу, и мы получим координаты в новом базисе! В OpenGL эта матрица называется матрицей вида (view matrix).
Viewport
Если вы помните, то у меня в коде встречались подобные конструкции:
screen_coords[j] = Vec2i((v.x+1.)*width/2., (v.y+1.)*height/2.);
Что это означает? У меня есть точка Vec2f v, которая принадлежит квадрату [-1,1]*[-1,1]. Я хочу её нарисовать на картинке размером (width, height). Вектор (v.x+1) меняется в пределах от 1 до 2, (v.x+1.)/2. в пределах от нуля до единицы, ну а (v.x+1.)*width/2. заметает всю картинку, что мне и надо.
Но мы переходим к матричному представлению аффинных отображений, поэтому давайте рассмотрим следующий код:
Matrix viewport(int x, int y, int w, int h) {
Matrix m = Matrix::identity(4);
m[0][3] = x+w/2.f;
m[1][3] = y+h/2.f;
m[2][3] = depth/2.f;
m[0][0] = w/2.f;
m[1][1] = h/2.f;
m[2][2] = depth/2.f;
return m;
}
Он строит вот такую матрицу:
Это означает, что куб мировых координат [-1,1]*[-1,1]*[-1,1] отображается в куб экранных координат (да, куб, т.к. у нас есть z-буфер!) [x,x+w]*[y,y+h]*[0,d], где d — это разрешение z-буфера (у меня 255, т.к. я храню его непосредственно в чёрно-белой картинке).
В мире OpenGL эта матрица называется viewport matrix.
Цепь преобразований
Итак, резюмируем. Модели (например, пресонажи) сделаны в своей локальной системе координат (object coordinates). Они вставляются в сцену, которая выражена в мировых координатах (world coordinates). Переход от одних к другим осуществляется матрицей Model. Дальше, мы хотим выразить это дело в репере камеры (eye coordinates), матрица перехода от мировых к камере называется View. Затем, мы осуществляем перспективное искажение при помощи матрицы Projection (см. статью 4а), она переводит сцену в так называемые clip coordinates. Ну и затем мы отображаем это всё дело на экране, матрица прехода к экранным координатам это Viewport.
То есть, если мы прочитали точку v из файла, то чтобы показать её на экране, мы проделываем умножение
Viewport * Projection * View * Model * v.
Если посмотреть в код на гитхабе, то мы увидим такие строчки:
Vec3f v = model->vert(face[j]); screen_coords[j] = Vec3f(ViewPort*Projection*ModelView*Matrix(v));
Так как я рисую только один объект, то матрица Model у меня просто единичная, я её объединил с матрицей View.
Преобразование нормальных векторов
Широко известен следующий факт:
Если у нас задана модель и уже посчитаны (или, например, заданы руками) нормальные вектора к этой модели, и эта модель подвергается (аффинному) преобразованию M, то нормальные вектора подвергаются преобразованию, обратному к транспонированному M.
Что-что?!
Этот момент остаётся магическим для многих, но на самом деле, ничего волшебного тут нет. Рассмотрим треугольник и вектор a, являющийся нормальным к его наклонной грани. Если мы просто растянем наше пространство в два раза по вертикали, то преобразованный вектор a перестанет быть нормальным к преобразованной грани.

Чтобы убрать весь налёт магии, нужно понять одну простую вещь: нам нужно не просто преобразовать нормальные вектора, нам нужно посчитать нормальные вектора к преобразованной модели.
Итак, у нас есть вектор нормали a=(A,B,C). Мы знаем, что плоскость, проходящая через начало координат, и имеющая нормалью вектор a (на нашей иллюстрации это наклонное ребро левого треугольника), задаётся уравнением Ax+By+Cz=0. Давайте запишем это уравнение в матричном виде, причём сразу в однородных координатах:
Напоминаю, что (A,B,C) — это вектор, поэтому получает ноль в последнюю компоненту при погружении в четырёхмерное пространство, а (x,y,z) — это точка, поэтому к нему приписываем 1.
Давайте добавим единичную матрицу (М, умноженная на обратную к ней) в середину этой записи:
Выражение в правых скобках — это преобразованные точки. В левых — нормальный вектор! Так как в стандартной конвенции при линейном отображении мы записываем векторы (и точки) в столбец (надеюсь, мы не будем разжигать холивара про ко- и контравариантные вектора),
то предыдущее выражение может быть записано следующим образом:
Что ровно приводит нас к вышеозначенному факту, что нормаль к преобразованному объекту получается преобразованием исходной нормали, обратным к транспонированному M.
Заметьте, если M — это композиция параллельных переносов, вращений и однородных растягиваний, то транспонированная М равняется обратной М, и они друг друга аннулируют. Но так как наши матрицы преобразований будут включать в себя перспективное искажение, это нам мало поможет.
В текущем коде мы преобразование нормалей не используем, но вот в следующей статье про шейдеры это будет очень важно.
Счастливого программирования!
Автор: haqreu