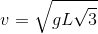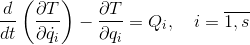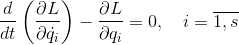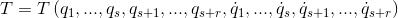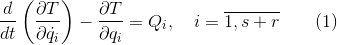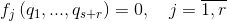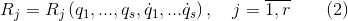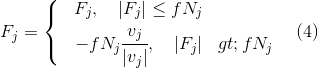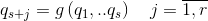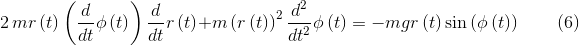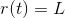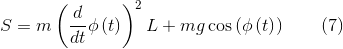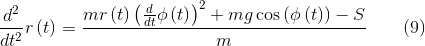Maple: составление уравнений Лагранжа 2 рода и метод избыточных координат

Предисловие

По роду профессиональной и научной деятельности я механик. Преподаю теоретическую механику в университете, пишу докторскую диссертацию в области динамики подвижного состава железных дорог. В общем, эта наука поглощает большую часть моего рабочего и даже свободного времени.

С Maple (на кафедре была 6-я версия, а у лоточников домой была куплена 8-я) познакомился ещё студентом, когда начинал работать над будущей кандидатской под крылом моего первого (ныше покойного) научного руководителя. Были и добрые люди, что помогли на самом первом этапе разобраться с пакетом и начать работать.

И вот так постепенно на его плечи была переложена большая часть вычислительной работы по подготовке диссертации. Диссертация была защищена, а Maple навсегда остался надёжным помошником в научном труде. Часто бывает необходимо быстро оценить какую-нибудь задачу, составить уравнения, исследовать их аналитически, быстро получить численное решение, построить графики. В этом отношении Maple просто незаменим для меня (ни в коем разе не хочу обидеть приверженцев других пакетов).

Сделать всё то, что будет предложено читателю под катом, меня задача принесенная ученицей (приходится ещё заниматься и репетиторством) со школьной олимпиады. Условие задачи таково:

Груз, висящий на нити длины L = 1,1 м, привязанной к гвоздю, толкнули так, что он поднялся, а затем ударился в гвоздь. Какова его скорость в момент удара о гвоздь? Ускорение свободного падения g = 10 м/с².

Если не придираться к некоторонной туманности условия, то задача достаточно проста, а её решение, полученное путем довольно громоздких для школьника выкладок, в общем виде дает результат

И вот тут захотелось проверить решение, полученное с оглядкой на школьную программу по физике независимым способом, например составив дифференциальные уравнения движения этого маятника, да не просто, а с учетом освобождения от связи (в процессе движения нить, считаемая невесомой, провисает и маятник движется как свободная точка).

Это послужило катализатором для того, чтобы взять да и откопать свои старые задумки, накопленные ещё со времен работы в оргкомитете Всероссийской Олимпиады студентов по теоретической механике — три года подряд занимался там подготовкой задач компьютерного конкурса. Задумки касались автоматизации построения уравнений движений для механических систем с неудерживающими связями и трением, используя известные всем уравнения Лагранжа 2 рода

поборов стереотип многих преподавателей о том, что уравнения эти неприменимы к системам с неудерживающими связями и трением.

Что касается Maple, то его библиотека для решения задач вариационного исчисления дает возможность быстро получить уравнения Эйлера-Лагранжа, решение которых минимизирует действие по Гамильтону, что применимо для консервативных систем

где 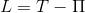— функция Лагранжа, равная разности кинетической и потенциальной энергий системы.

Так как расматриваемые задачи не относятся к классу консервативных, то автором была предпринята попытка самостоятельно реализовать автоматизацию построения и анализа уравнений движений. Что из этого вышло, изложено под катом

1. Метод избыточных координат

Рассматриваем механическую систему, имеющую s степеней свободы, положение которой описывается вектором обобщенных координат . Пусть также имеется r неудерживающих связей, к числу реакций которых можно причислить и трение покоя, при превышении предельного значения переходящее в активную силу трения скольжения, направление которой противоположно направлению относительной скорости скольжения.

Учет неудерживающих связей требует от нас определения и анализа величины их реакций, поэтому необходимо так же определить их величину. Уберем указанные связи и введем дополнительно r обобщенных координат, выразив через них кинетическую энергию системы

Составим s + r уравнений движения в форме уравнений Лагранжа 2 рода

содержащие s+r неизвестных координат и r неизвестных реакций связей. Считая связи удерживающими, дополняем данную систему уравнениями связей (для простоты рассматривая геометрические связи) в виде

получаем замкнутую систему уравнений, из которой находятся значения реакций

являющиеся функциями первых s (независимых) обобщенных координат и скоростей и они могут быть расчитаны на любом шаге интегрирования уравнений движения (1). Для удерживающих связей типа «нить/поверхность» уравнения (1) и (2) надо дополнить условием освобождения от связи

а для свзяей с сухим трением вида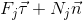

где F_j и N_j соответственно касательная и нормальная составляющая реакции; v_j — проекция скорости относительного проскальзывани точки приложения реакции.

Таким образом, уравнения (1) — (4) представляют собой полную математическую модель движения рассматриваемой механической системы.

Засим с теорией можно покончить и перейти к практике

2. Maple-функции построения и анализа уравнений Лагранжа

Для решения этой задачи была написана Maple-библиотека lagrange, содержащая четыре функции

LagrangeEQs — построение уравнений движения в форме Лагранжа 2 рода

LagrangeEQs := proc(T, q, r, F)

 local s := numelems(q);
 local n := numelems(rk);
 local i, k;
 local T1, dT1dv;
 local dTdv, dTdvdt;
 local T2, dT2dq;
 local dTdq;
 local left_part;
 local Q;
 local summa;
 local r1, dr1dq, drdq;

 # Получение левой части уравнений движения
 for i from 1 to s do
  
  # Дифференцируем кинетическую энергию по обобщенным скоростям и времени
  T1[i] := subs(diff(q[i], t) = v[i], T);
  dT1dv[i] := diff(T1[i], v[i]);
  dTdv[i] := subs(v[i] = diff(q[i], t), dT1dv[i]);
  dTdvdt[i] := diff(dTdv[i], t);

  # Дифференцируем кинетическую энергию по обобщенным координатам
  T2[i] := subs(q[i] = q1[i], T);
  dT2dq[i] := diff(T2[i], q1[i]);
  dTdq[i] := subs(q1[i] = q[i], dT2dq[i]);
  
  # Формируем левую часть уравнения движения
  left_part[i] := expand(simplify(dTdvdt[i] - dTdq[i]));
 end do;

 VectorCalculus[BasisFormat](false);

 # Вычисляем обобщенные силы (правая часть уравнений движения)
 for i from 1 to s do
  summa := 0;
  for k from 1 to n do

   # Дифференцируем радиус-ректор точки приложения k-й силы по i-й обобщенной координате
   r1[k] := subs(q[i] = q1[i], r[k]);
   dr1dq[k] := VectorCalculus[diff](r1[k], q1[i]);
   drdq[k] := subs(q1[i] = q[i], dr1dq[k]);
   
   # Скалярно перемножаем вектор силы на производную от радиус-вектора по обобщенной координате 
   # и накапливаем результат
   summa := summa + LinearAlgebra:-DotProduct(F[k], drdq[k], conjugate = false); 
  end do;

  Q[i] := expand(simplify(summa));
 end do;

 # Окончательно формируем уравнения и возвращаем результатq
 return {seq(left_part[i] = Q[i], i=1..s)};

end proc:

В качестве входных параметров функция принимает выражение кинетической энергии T как функцию обобщенных координат и обобщенных скоростей; массив обобщенных координат q; массив радиус-векторов точек приложения сил r и массив векторов сил F.

LinksEQs — получение уравнений дифференциальных связей из уравнений геометрических связей

LinksEQs := proc(eqs)

 local Eq1, Eq2;
 local i;
 local r := numelems(eqs);
 
 # Дважды дифференцируем уравнения связей по времени
 for i from 1 to r do
  Eq1[i] := diff(lhs(eqs[i]), t) = diff(rhs(eqs[i]), t);
  Eq2[i] := diff(diff(lhs(eqs[i]), t), t) = diff(diff(rhs(eqs[i]), t), t);
 end do;

 # и возвращаем результат
 return {seq(eqs[i], i=1..r), seq(Eq1[i], i=1..r),seq(Eq2[i], i=1..r)};

end proc:

Здесь надо отметить, что система уравнений геометрических связей eqs должна содержать избыточные координаты в явном виде, то есть иметь вид

в противном случае функции библиотеки не смогут обработать уравнения правильно. Для тестирования возможностей библиотеки сойдет и так, но в дальнейшем этот момент будет переработан: просто пока неясно, будет ли гарантированно разрешена система уравнений связи относительно угловых избыточных координат.

ReduceSystem — преобразование уравнений движения с учетом уравнений связей

ReduceSystem := proc(eqs, links, q)

 local i, j, k;
 local links_eqs := LinksEQs(links);

 local r := numelems(links_eqs);
 local s := numelems(q);

 local eq := [seq(eqs[i], i=1..s)];

 for i from 1 to s do
  for j from 1 to r do
   eq[i] := simplify(algsubs(links_eqs[j], eq[i]));
  end do:
 end do:

 return {seq(eq[i], i=1..s)};

end proc:

Данный код в подробных пояснениях не нуждается — тут выполняется подстановка избыточных обобщенных координат, скоростей и ускорений, выражаемых уравнениями геометрических и дифференциальных связей в уравнения движения, с целью приведения их к виду, пригодному для вычисления реакций неудерживающих связей

SolveAccelsReacts — решение уравнений движения относительно реакций и обобщенных ускорений

SolveAccelsReacts := proc(eqs, q, R)

 local s := numelems(q);
 local r := numelems(R);

 # Формируем вектор переменных, относительно которых будем решать уравнения движения
 local vars := [seq(diff(diff(q[i], t), t), i=1..s), seq(R[i], i=1..r)];
 local eq := [seq(eqs[i], i=1..numelems(eqs))];
 local i, j;
 local x;
 local solv;
 
 # Вводим подстановку - заменяем "иксами" все искомые переменные
 for i from 1 to numelems(eqs) do
  for j from 1 to s + r do
   eq[i] := subs(vars[j] = x[j], eq[i]);
  end do:
 end do;

 # ищем "иксы" (система всегда линейна относительно них)
 solv := solve({seq(eq[i], i=1..numelems(eq))}, {seq(x[i], i=1..s+r)});

 # Связываем иксы с найденными значениями
 assign(solv);

 # Возвращаем уравнения, решенные относительно обобщенных ускорений и реакций
 return {seq(vars[i] = x[i], i=1..s+r)};

end proc:

Данная функция принимает на вход систему уравнений движения eqs, преобразованную с учетом уравнений связей. Она линейна относительно вторых производных независимых координат и реакций связей. Другие входные параметры: q — вектор независимых координат; R — массив реакций, относительно которых необходимо разрешить уравнения движения.

Теперь проиллюстрируем, как применять описанное «хозяйство» в деле

3. Задача о маятнике на тонкой нерастяжимой нити

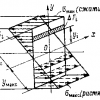
Расчетная схема будет такой. В качетве обобщенной координаты выбираем угол 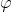наклона нити к вертикали.

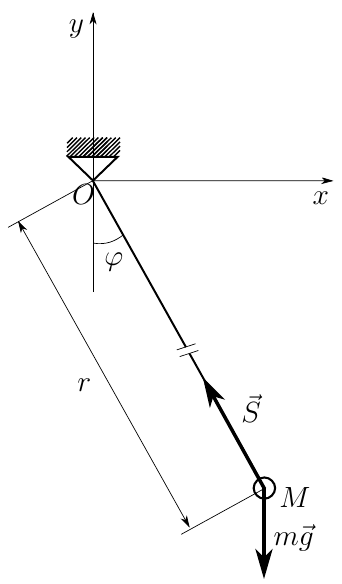
Поскольку нить — неудерживающая связь, нас будет интересовать её реакция, а значит введем дополнительную, избыточную координату r(t).

Приступаем. Чистим память и подключаем библиотеку линейной алгебры

restart;
with(LinearAlgebra):

Подключаем библиотеку lagrange

read `/home/maisvendoo/work/maplelibs/mechanics/lagrange.m`;

Определяем вектор обобщенных координат, вычисляем координаты и скорость груза, а так же кинетическую энергию системы

q := [r(t), phi(t)];

xM := q[1]*sin(q[2]);
yM := -q[1]*cos(q[2]);

vMx := diff(xM, t);
vMy := diff(yM, t);

T := simplify(m*(vMx^2 + vMy^2)/2);

На выходе получаем выражение для кинетической энергии (для вставки сюда использована функция latex(), генерирующая результат в LaTeX-нотации)

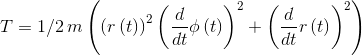
Формируем массив сил и массив координат точек их приложения

Mg := Vector([0, -m*g]);
React := Vector([-S*sin(q[2]), S*cos(q[2])]);
rM := Vector([xM, yM]);
Fk := [Mg, React];
rk := [rM, rM];

Скармливаем всё функции LagrangeEQs()

EQs := LagrangeEQs(T, q, rk, Fk):

получая на выходе уравнения движения

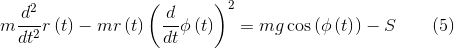
Нетрудно убедится, что функция отработала нормально — для иллюстрации специально выбрана не слишком громоздкая задача.

Далее задаем уравнение связи — пока нить натянута, справедливо условие

преобразуем систему с учетом этого условия и находим реакцию связи

link_eqs := {r(t) = L};
simple_eqs := ReduceSystem(EQs, link_eqs, q); 
solv1 := SolveAccelsReacts(simple_eqs, [phi(t)], [S]);

Сила натяжения нити равна

Система (5) — (7) является полной системой уравнений движения груза, с учетом возможности провисания нити. Теперь подготовим её к численному интегрированию. Для начала разрешим её относительно ускорений, передав в SolveAccelsReacts() уравнения (5) и (6), вектор обобщенных координат и пустой массив реакций

EQs2 := SolveAccelsReacts(EQs, q,[]);

получая на выходе

Для численного моделирования, хоть это и не спортивно, напишем отдельный код, дабы не забивать голову читателя длительной обработкой полученной системы напильником. Тем более что моделирование будет иметь свои особенности.

Готовим исходные данные и систему уравнений движения

L := 1.1:
g := 10.0:

# Функция вычисляет производные фазовых координат
EQs_func := proc(N, t, Y, dYdt)
 # Ускорение силы натяжения нити (as = S/m)
 local as := 0;
 # Если нить уже провисла, то реакции нет
 if Y[1] < L then
  as := 0;
 else 
  # Если нить натянута, вычисляем ускорение её реакции
  as := L*Y[4]^2 + g*cos(Y[2]);
  # Если оно отрицательно - нить провисла, реакции нет
  if as < 0 then as := 0; end if;
 end if;

 # Собственно система уравнений в форме Коши 
 # Y[1] -> r(t)  - расстояние от груза до гвоздя
 # Y[2] -> phi(t) - угол радиус-вектора груза к вертикали
 # Y[3] -> vr(t) - радиальная скорость груза 
 # Y[4] -> omega(t) - угловая скорость поворота радиус-вектора
 dYdt[1] := Y[3];
 dYdt[2] := Y[4];
 dYdt[3] := Y[1]*Y[4]^2 + g*cos(Y[2]) - as;
 dYdt[4] := -(2*Y[3]*Y[4] + g*sin(Y[2]))/Y[1];
end proc:

Строим функцию вычисления состояния системы, при заданной горизонтальной начальной скорости груза

sys_pos := proc(v0)

 # Формируем начальные условия
 local initc := Array([L, 0, 0, v0/L]);
 # Задаем функции, которые ищем
 local q := [r(t), phi(t), vr(t), omega(t)];

 # Численно решаем систему ОДУ движения
 local dsolv := dsolve(numeric, number = 4, procedure = EQs_func, start = 0, initial = initc,  procvars = q, output=listprocedure);

 # Выделяем из решения полученные функции
 local R := eval(r(t), dsolv);
 local Phi := eval(phi(t), dsolv);
 local Vr := eval(vr(t), dsolv);
 local Omega := eval(omega(t), dsolv);

 return [R, Phi, Vr, Omega]; 

end proc:

Теперь проверяем «школьное» решение задачи

# Такая начальная скорость должна быть, согласно школьному решению задачи
v0 := evalf(sqrt(g*L*(2 + sqrt(3)))):

# Погрешность попадания груза в гвоздь
eps := 1e-5:

# Интегрируем уравнения и получаем решение
r := sys_pos(v0)[1]:
phi := sys_pos(v0)[2]:
vr := sys_pos(v0)[3]:

# Строим декартовы координаты груза
x := t->r(t)*sin(phi(t)):
y := t->-r(t)*cos(phi(t)):

# Определяем момент удара о гвоздь
t1 := fsolve(r(t) = eps, t=0..10.0):

# Вычисляем скорость в момент удара
v  := vr(t1);

# Строим траекторию груза
plot([x(t), y(t), t=0..t1], view=[-L..L, -L..L]);

В итоге, получаем результат, приведенный на скриншоте. Скорость груза в момент удара соответствует приведенному в предисловии значению, и видно, что до провисания нити груз движется по окружности, а после провисания нити движется как свободная точка под действием силы тяжести, по параболе.

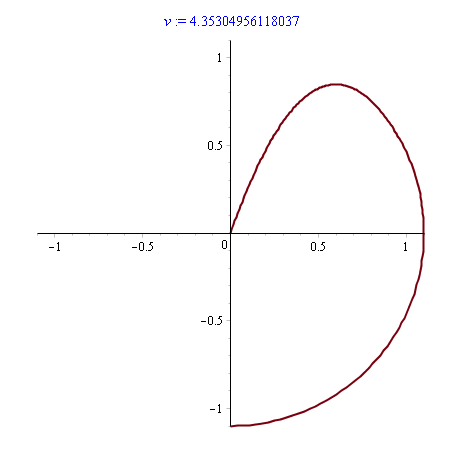
Замечу, что погрешности попадания в гвоздь — вынужденная мера: в полярных координатах, которые были использованы, задача имеет особенность, понятную из уравнения (8). Поэтому r(t) сравнивалось не с нулем, а с величиной eps достаточно малой, чтобы получить решение, и достаточно большой, чтобы численный решатель fsolve() не сходил с ума. Однако это нисколько не умаляет практической ценности изложенных результатов.

Вместо заключения

Возможно, читатель упрекнет меня, что я стреляю из пушки по воробьям. Однако, хочется заметить, что всё сложное начинается с простого, а большая наука — с малых задач.

Тестовую версию библиотеки можно качнуть тут

Благодарю за внимание к моему труду )

Автор: maisvendoo

Источник