Вступление
Эта публикация является первой частью краткого вступления с иллюстрациями в вероятностное программирование, которое является одним из современных прикладных направлений машинного обучения и искусственного интеллекта. Во время написания этой публикации я с радостью обнаружил, что на Хабрахабре совсем недавно уже была статья о вероятностном программировании с рассмотрением прикладных примеров из области теории познания, хотя, к сожалению, в русскоговоряющем Интернете пока мало материалов на эту тему.
Я, автор, Юра Перов, занимаюсь вероятностным программированием в течение уже двух лет в рамках своей основной учебно-научной деятельности. Продуктивное знакомство с вероятностным программированием у меня сложилось, когда будучи студентом Института математики и фундаментальной информатики Сибирского федерального университета, я проходил стажировку в Лаборатории компьютерных наук и искусственного интеллекта в Массачусетском технологическом институте под руководством профессора Джошуа Тененбаума и доктора Викаша Мансингхи, а затем продолжилось на Факультете технических наук Оксфордского университета, где на данный момент я являюсь студентом-магистром под руководством профессора Френка Вуда.
Вероятностное программирование я люблю определять как компактный, композиционный способ представления порождающих вероятностных моделей и проведения статистического вывода в них с учетом данных с помощью обобщенных алгоритмов. Хотя вероятностное программирование не вносит много фундаментального нового в теорию машинного обучения, этот подход привлекает своей простотой: «вероятностные порождающие модели в массы!»
«Обычное» программирование
Для знакомства с вероятностным программирование давайте сначала поговорим об «обычном» программировании. В «обычном» программировании основой является алгоритм, обычно детерминированный, который позволяет нам из входных данных получить выходные по четко установленным правилам.
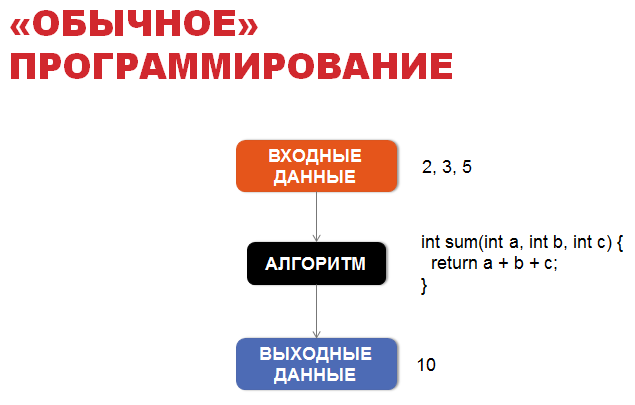
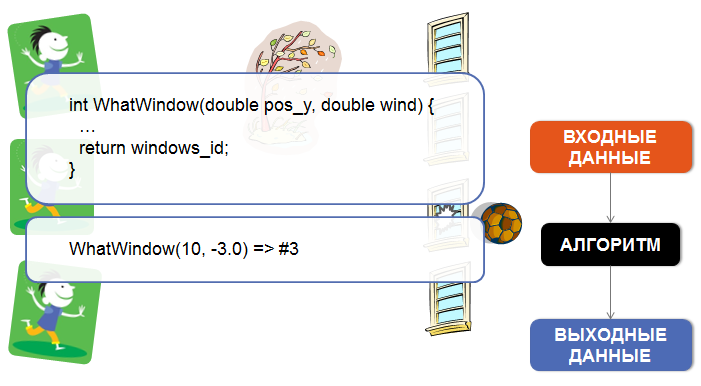
Например, если у нас есть мальчик Вася, и мы знаем где он находится, куда он бросает мяч и каковы внешние условия (например, сила ветра), мы узнаем, какое окно он, к сожалению, разобьет в здании школы. Для этого достаточно симулировать простые законы школьной физики, которые легко можно записать в виде алгоритма.
А теперь вероятностное программирование
Однако часто мы знаем только результат, исход, и мы заинтересованы в том, чтобы узнать то, какие неизвестные значения привели именно к этому результату? Чтобы ответить на этот вопрос с помощью теории математического моделирования создается вероятностная модель, часть параметров которой не определены точно.
Например, в случае с мальчиком Васей, зная то, какое окно он разбил, и имея априорные знания о том, около какого окна он и его друзья обычно играют в футбол, и зная прогноз погоды на этот день, мы хотим узнать апостериорные распределение местоположения мальчика Васи: откуда же он бросал мяч?

Итак, зная выходные данные, мы заинтересованы в том, чтобы узнать наиболее вероятные значения скрытых, неизвестных параметров.
В рамках машинного обучения рассматриваются в том числе порождающие вероятностные модели. В рамках порождающих вероятностных моделей модель описывается как алгоритм, но вместо точных однозначных значений скрытых параметров и некоторых входных параметров мы используем вероятностные распределениях на них.
Существует более 15 языков вероятностного программирования, перечень с кратким описанием каждого из них можно найти здесь. В данной публикации приведен пример кода на вероятностных языках Venture/Anglican, который имеют очень схожий синтаксис и которые берут свое начало от вероятностного языка Church. Church в свою очередь основан на языке «обычного» программирования Lisp и Scheme. Заинтересованному читателю крайне рекомендуется ознакомиться с книгой «Структура и интерпретация компьютерных программ», являющейся одним из лучших способов начать знакомство с языком «обычного» программирования Scheme.
Пример Байесовской линейной регрессии
Рассмотрим задание простой вероятностной модели Байесовской линейной регрессии на языке вероятностного программирования Venture/Anglican в виде вероятностной программы:
01: [ASSUME t1 (normal 0 1)]
02: [ASSUME t2 (normal 0 1)]
03: [ASSUME noise 0.01]
04: [ASSUME noisy_x (lambda (time) (normal (+ t1 (* t2 time)) noise))]
05: [OBSERVE (noisy_x 1.0) 10.3]
06: [OBSERVE (noisy_x 2.0) 11.1]
07: [OBSERVE (noisy_x 3.0) 11.9]
08: [PREDICT t1]
09: [PREDICT t2]
10: [PREDICT (x 4.0)]
Скрытые искомые параметры — значения коэффициентов t1 и t2 линейной функции x = t1 + t2 * time. У нас есть априорные предположения о данных коэффициентах, а именно мы предполагаем, что они распределены по закону нормального распределения Normal(0, 1) со средним 0 и стандартным отклонением 1. Таким образом, мы определили в первых двух строках вероятностной программы априорную вероятность на скрытые переменные, P(T). Инструкцию [ASSUME name expression] можно рассматривать как определение случайной величины с именем name, принимающей значение вычисляемого выражение (программного кода) expression, которое содержит в себе неопределенность.
Вероятностные языки программирования (имеются в виду конкретно Church, Venture, Anglican), как и Lisp/Scheme, являются функциональными языками программирования, и используют польскую нотацию при записи выражений для вычисления. Это означает, что в выражении вызова функции сначала располагается оператор, а уже только потом аргументы: (+ 1 2), и вызов функции обрамляется круглыми скобками. На других языках программирования, таких как C++ или Python, это будет эквивалентно коду 1 + 2.
В вероятностных языках программирования выражение вызова функции принято разделять на три разных вида:
- Вызов детерминированных процедур (primitive-procedure arg1… argN), которые при одних и тех же аргументах всегда возвращают одно и то же значение. К таким процедурам, например, относятся арифметические операции.
- Вызов вероятностных (стохастических) процедур (stochastic-procedure arg1… argN), которые при каждом вызове генерируют случайным образом элемент из соответствующего распределения. Такой вызов определяет новую случайную величину. Например, вызов вероятностной процедуры (normal 1 10) определяет случайную величину, распределенную по закону нормального распределения Normal(1, sqrt(10)), и результатом выполнения каждый раз будет какое-то вещественное число.
- Вызов составных процедур (compound-procedure arg1… argN), где compound-procedure — введенная пользователем процедура с помощью специального выражения lambda: (lambda (arg1… argN) body), где body — тело процедуры, состоящее из выражений. В общем случае составная процедура является стохастической (недетерминированной) составной процедурой, так как ее тело может содержать вызовы вероятностных процедур.
Вернемся к исходному коду на языке программирования Venture/Anglican. После первых двух строк мы хотим задать условную вероятность P(X | T), то есть условную вероятность наблюдаемых переменных x1, x2, x3 при заданных значениях скрытых переменных t1, t2 и параметра time.
Перед вводом непосредственно самих наблюдений с помощью выражения [OBSERVE ...] мы определяем общий закон для наблюдаемых переменных xi в рамках нашей модели, а именно мы предполагаем, что данные наблюдаемые случайные величины при заданных t1, t2 и заданном уровне шума noise распределены по закону нормального распределения Normal(t1 + t2 * time, sqrt(noise)) со средним t1 + t2 * time и стандартным отклонением noise. Данная условная вероятность определена на строках 3 и 4 данной вероятностной программы. noisy_x определена как функция, принимающая параметр time и возвращающая случайное значение, определенное с помощью вычисления выражение (normal (+ t1 (* t2 time)) noise) и обусловленное значениями случайных величин t1 и t2 и переменной noise. Отметим, что выражение (normal (+ t1 (* t2 time)) noise) содержит в себе неопределенность, поэтому каждый раз при его вычислении мы будем получать в общем случае разное значение.
На строках 5—7 мы непосредственно вводим известные значения x1 = 10.3, x2 = 11.1, x3 = 11.9. Инструкция вида [OBSERVE expression value] фиксирует наблюдение о том, что случайная величина, принимающая значение согласно выполнению выражения expression, приняла значение value.
Повторим на данном этапе всё, что мы сделали. На строках 1—4 с помощью инструкций вида [ASSUME ...] мы задали непосредственно саму вероятностную модель: P(T) и P(X | T). На строках 5—7 мы непосредственно задали известные нам значения наблюдаемых случайных величин X с помощью инструкций вида [OBSERVE ...].
На строках 8—9 мы запрашиваем у системы вероятностного программирования апостериорное распределение P(T | X) скрытых случайных величин t1 и t2. Как уже было сказано, при большом объеме данных и достаточно сложных моделях получить точное аналитическое представление невозможно, поэтому инструкции вида [PREDICT ...] генерируют выборку значений случайных величин из апостериорного распределения P(T | X) или его приближения. Инструкция вида [PREDICT expression] в общем случае генерирует один элемент выборки из значений случайной величины, принимающей значение согласно выполнению выражения expression. Если перед инструкциями вида [PREDICT ...] расположены инструкции вида [OBSERVE ...], то выборка будет из апостериорного распределения (говоря точнее, конечно, из приближения апостериорного распределения), обусловленного перечисленными ранее введенными наблюдениями.
Отметим, что в завершении мы можем также предсказать значение функции x(time) в другой точке, например, при time = 4.0. Под предсказанием в данном случае понимается генерация выборки из апостериорного распределения новой случайной величины при значениях скрытых случайных величин t1, t2 и параметре time = 4.0.
Для генерации выборки из апостериорного распределения P(T | X) в языке программирования Venture в качестве основного используется алгоритм Метрополиса-Гастингса, который относится к методам Монте-Карло по схеме Марковских цепей. Под обобщенным выводом в данном случае понимается то, что алгоритм может быть применен к любым вероятностным программам, написанным на данном вероятностном языке программирования.
В видео, прикрепленном ниже, можно посмотреть на происходящий статистический вывод в данной модели.
В самом начале у нас нет данных, поэтому мы видим априорное распределение прямых. Добавляя точку за точкой (таким образом, элементы данных), мы видим элементы выборки из апостериорного распределения.
На этом мы закончим первую часть данного вступления в вероятностное программирование.
Материалы
Ниже я приведу рекомендуемые ссылки для тех, кто хочет прямо сейчас узнать больше о вероятностном программировании:
- Сайт вероятностного языка программирования Anglican, являющийся собратом Venture и потомком Church.
- Обучающий курс по вероятностному языку программирования Anglican.
- Курс по вероятностному программированию, прочитанный на одной из школ по машинному обучению: часть 1, часть 2 и часть 3.
- Курс «Проектирование и реализация вероятностных языков программирования».
- Курс «Вероятностные порождающие модели познания (одна из сфер применения вероятностного программирования)».
Данная публикация основана на моей бакалаврской научной работе, которая была защищена летом этого года в Институте математики и фундаментальной информатики Сибирского федерального университета. Заинтересованный читатель найдет в ней более подробное и формальное введение в вероятностное программирование. В работе в конце также есть вся полная библиография, на основе которой написана и данная публикация.
Автор: YuraPerov





