 В 1994 году Даниэль Саймон опубликовал статью «О мощи квантовых вычислений», в которой описал алгоритм, позже названный его именем, имеющий экспоненциальное превосходство над имеющимися алгоритмами в рамках классической вычислительной модели. Задача, которую решает этот алгоритм, является не такой оторванной от реальности, как задача Дойча, хотя и ещё несколько абстрактной. Тем не менее, эта задача и представленный алгоритм вызвали огромный интерес у исследователей, и в дальнейшем алгоритм Саймона стал основой ряда квантовых алгоритмов, в том числе и для алгоритмов Шора факторизации целых чисел и вычисления дискретного логарифма.
В 1994 году Даниэль Саймон опубликовал статью «О мощи квантовых вычислений», в которой описал алгоритм, позже названный его именем, имеющий экспоненциальное превосходство над имеющимися алгоритмами в рамках классической вычислительной модели. Задача, которую решает этот алгоритм, является не такой оторванной от реальности, как задача Дойча, хотя и ещё несколько абстрактной. Тем не менее, эта задача и представленный алгоритм вызвали огромный интерес у исследователей, и в дальнейшем алгоритм Саймона стал основой ряда квантовых алгоритмов, в том числе и для алгоритмов Шора факторизации целых чисел и вычисления дискретного логарифма.
Эта статья является продолжением в цикле статей по модели квантовых вычислений, поэтому если начать читать её без ознакомления с предыдущими статьями цикла, что-то может показаться непонятным. Так что читателя, который впервые набрёл на эти мои заметки, я отправляю к первым статьям: 1, 2, 3, 4, 5.
Всех, кому интересна эта тема и кто следит за моими публикациями в рамки исследования модели квантовых вычислений, приглашаю воспоследовать под кат, чтобы изучить алгоритм с точки зрения программиста.
Математическая постановка задачи
Задача Саймона звучит следующим образом. Пусть дана двоичная функция f: {0, 1}n → {0, 1}m, при этом m ≥ n. Кроме того известно, что данная функция является либо взаимно однозначной, либо имеется некоторое число s ∈ {0, 1}n, называемое периодом, что для любой пары различных входных значений x и x' функция f возвращает одинаковое значение тогда и только тогда, когда x' = x ⊕ s. Для заданной функции, удовлетворяющей этим условиям, необходимо найти период s.
Другими словами, алгоритм Саймона возвращает следующее значение:
- s, если существует нетривиальная (не равная 0n) строка s такая, что ∀x' ≠ x ∶ f(x' ) = f(x) ⇔ x' = x ⊕ s.
- 0, если функция f взаимно однозначная.
- Неопределено, в противном случае.
Алгоритм Саймона вычисляет период функции s за линейное время (и линейное количество вызовов оракула), в то время как любому классическому алгоритму требуется экспоненциальное время в зависимости от длины входного аргумента функции.
Квантовая схема
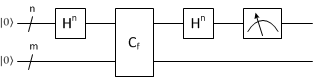
Для получения периода s с большой вероятностью (алгоритм Саймона, как полагается, является вероятностным алгоритмом) необходимо повторить полиномиальное от длины входного слова число раз следующую процедуру:
- Применить к входному регистру
|0n>преобразование Адамара для n кубитов. - Применить к полному набору кубитов оракул Cf.
- Вновь применить только к входному регистру преобразование Адамара. После этого входной регистр необходимо измерить для получения значения (x' ⊕ s).
Применив эту последовательность шагов не более (n — 1) раз, можно доподлинно восстановить значение периода s.
Диаграмма квантовой схемы описанного алгоритма выглядит следующим образом:
Реализация на языке Haskell
Давайте, как это принято, попробуем реализовать пример такой квантовой схемы при помощи ранее разработанного набора функций для квантовых вычислений, который мы уже неоднократно использовали ранее в описании квантовых алгоритмов. При необходимости этот набор будет дорабатываться. Для этого, как полагается, выберем тестовую функцию и запроектируем оракул для неё.
В качестве функции предлагается рассмотреть такую: f: {0, 1}2 → {0, 1}2, поскольку в этом случае входов и выходов будет по 4, а это значит, что размеры матриц будут 16×16. Похоже, что это предел для выполнения упражнений на бумаге, поэтому остановимся на таком варианте. Однако читателя никто не ограничивает, и в качестве упражнений для тренировки можно рассмотреть и функции более высоких размерностей.
Пусть дана некоторая функция, которая определена следующим образом:
targetF :: (Bool, Bool) -> (Bool, Bool)
targetF (False, False) = (False, True)
targetF (False, True) = (False, True)
targetF (True, False) = (True, False)
targetF (True, True) = (True, False)
Здесь использован некаррированный вариант передачи входных аргументов, и это сделано исключительно для единообразия кода. Как видно, эта функция представляет собой описание следующей таблицы истинности:
| X1 | X2 | f(X1) | f(X2) |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
Если внимательно присмотреться, то станет понятно, что периодом s в данном случае является строка (0, 1), поскольку значение функции одинаково для любой пары (x1, x2) и (x1 ⊕ 0, x2 ⊕ 1) = (x1, x2). Такая функция подходит под задачу Саймона, а потому может быть использована для исследования реализации алгоритма.
Для построения оракула, как это обычно бывает, воспользуемся табличной техникой. Вот таблица, которая показывает то, как оракул должен преобразовывать входные кубиты.
| X1 | X2 | Y1 | Y2 | f(X1, X2) | f(X1, X2) ⊕ (Y1, Y2) | Преобразование | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |0000> → |0001> |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |0001> → |0000> |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | |0010> → |0011> |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | |0011> → |0010> |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | |0100> → |0101> |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | |0101> → |0100> |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |0110> → |0111> |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | |0111> → |0110> |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | |1000> → |1010> |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | |1001> → |1011> |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | |1010> → |1000> |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | |1011> → |1001> |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | |1100> → |1110> |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | |1101> → |1111> |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | |1110> → |1100> |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | |1111> → |1101> |
Этой таблице соответствует следующая матрица (сразу пишем её на языке Haskell, чтобы не тратить время и место):
oracle :: Matrix (Complex Double)
oracle = matrixToComplex
[[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]]
Теперь реализуем непосредственно функцию, которая кодирует представленную ранее квантовую схему алгоритма Саймона для случая f: {0, 1}2 → {0, 1}2. Вот очень несложное определение:
simon :: Matrix (Complex Double) -> IO String
simon o = initial |> gateH2I2
|> o
|> gateH2I2
>>> (measure . fromVector 4)
where
initial = toVector $
foldr entangle qubitZero $
replicate 3 qubitZero
gateH2I2 = gateHn 2 <++> gateIn 2
Как видно, здесь опять представлена техника, которая позволяет писать код, очень похожий на сами квантовые схемы. При помощи операции (|>) собираются последовательности гейтов, через которые пропускается квантовый регистр кубитов.
В данном случае в локальном определении initial создаётся квантовое состояние |0000>, которое затем пропускается через гейт gateH2I2, тоже определённый локально. Этот гейт представляет собой преобразование Адамара, применённое к первым двум кубитам четырёхкубитного регистра, а вторые два кубита остаются без изменений (к ним применяется гейт I, не изменяющий квантового состояния).
Далее всё делается в соответствии с алгоритмом и его квантовой схемой.
Поскольку алгоритм является вероятностным, имеет смысл реализовать функцию main для многократного запуска функции simon и сбора результатов её исполнения. Определим её следующим образом:
main :: Int -> IO [(Int, String)]
main n = do l <- replicateM n $ simon oracle
return $
map (length &&& head) $
group $
sort l
Если запустить эту функцию с достаточно большим параметром (я запускал со значением 1 000 000), то на выходе будут достаточно достоверные значения частотных вероятностей измерения того или иного результата. В данном конкретном примере в качестве результатов будут такие значения квантовых состояний: |0001>, |0010>, |1001> и |1010>, и все они будут иметь вероятность получения примерно 25 % (а в теории так ровно 0.25). Однако, честно говоря, в соответствии с буквой алгоритма надо измерять только входной регистр, то есть в данном случае первые два кубита. Это значит, что вероятности квантовых состояний |0001> и |0010> надо просто сложить, чтобы получить вероятность получения квантового состояния |00> для первых двух кубитов. Другими словами, в этом примере в результате измерения входного регистра будут равновероятно получаться значения |00> и |10>.
Результат |00> является «тривиальным» и нас не интересует (поскольку какое бы значение не складывать по модулю 2 со значением 0, будет получаться исходное значение) — нулевое значение всегда является «тривиальным периодом» для любой двоичной функции. Так что остаётся только другое нетривиальное значение, и оно равно |10>, как и было загадано.
Заключение
Для закрепления пройденного к настоящему моменту материала вдумчивому читателю рекомендуется несколько несложных упражнений по этой теме:
- Реализация функции
makeOracleдля автоматического создания оракулов произвольной размерности. - Исследование алгоритма для функции, у которой есть только нулевой период (которая является перестановкой).
- Исследование алгоритма для функций, у которых есть больше одного периода (а можно ли построить такую функцию?).
После выполнения этих задач можно перейти уже к следующим алгоритмам, которые представляют наибольший интерес в рамках изучения модули квантовых вычислений.
Код, описанный в этой небольшой заметке, всякий желающий может получить здесь.
Мои предыдущие статьи по теме квантовых вычислений:
- Слово малое об обратимых вычислениях
- Реализация алгоритма Дойча на языке Haskell
- Квантовая схемотехника: некоторые приёмы и техники
- Разворачиваем язык квантового программирования Quipper
- Продолжаем изучать квантовые вычисления: алгоритм Дойча-Йожи
- Квантовый поиск при помощи алгоритма Гровера
Автор: Darkus






