Нил Форд, Архитектор ПО, ThoughWorks Inc.
03 Апреля 2012
перевод статьи Functional thinking: Functional design patterns, Part 2
В последней части (на хабре), я начал исследование взаимодействия традиционных шаблонов “Банды четырех” (Gang of Four, GoF) и более функциональных подходов. Я продолжу разбор в этой части, показывая решение типичных проблем в рамках 3х различных парадигм: паттерны, метапрограммирование и композиция функций.
Если первичная парадигма, которая поддерживается вашим ЯП объектная, то намного проще думать о решении каждой проблемы в рамках ее терминов. Тем не менее, большинство современных языков программирования являются мультипарадигменными, это значит, что они поддерживают объекты, метаобъекты, функциональную и другие парадигмы. Изучение использования различных парадигм для наиболее подходящего решения проблемы — часть эволюции в лучшего разработчика.
В этой части, я собираюсь разобрать традиционную проблему, решаемую с помощью шаблона проектирования “Адаптер”: организация интерфейса для работы с неподходящим интерфейсом. Первым делом, традицонный подход, реализованный на Java.
“Адаптер” на Java
Шаблон «Адаптер» преобразует интерфейс неподходящего класса в такой, с которым можно работать. Он используется когда два класса концептуально могут работать друг с другом, но не делают этого из-за деталей реализации. Например, я создаю несколько простых классов, моделируя проблему попадания квадратного колышка в круглое отверстие (прим.перев: «square pegs and round holes», далее я буду использовать сочетание «квадрат и окружность», для упрощения). Квадрат помещается в окружность, как показано на рисунке, в зависимости от соответствующих размеров окружности и квадрата.
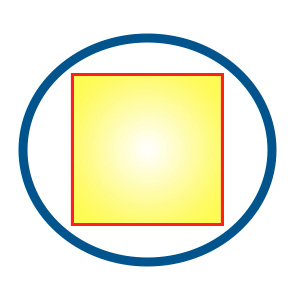
Рисунок 1
Для того чтобы определить будет ли квадрат помещаться в окружность, я использую формулу на рисунке 2.
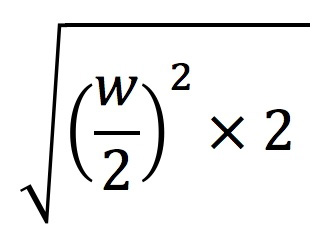
Рисунок 2
Формула, на рисунке 2, вычисляет корень квадратный произведения: половины стороны данного квадрата в степени 2 на число 2. Если значение этой формулы будет меньше, чем радиус окружности, то квадрат будет помещаться.
Я мог бы тривиально решить эту проблему с помощью вспомогательного класса, который делает преобразования. Однако, это хороший пример большей проблемы. Например, что если я хочу адаптировать Кнопку (Button) так, чтоб она помещалась на Панель (Panel) некоторого типа, дизайн которой не предполагал такой возможности, могу ли я это сделать? Проблема окружность/квадрат это удобное упрощение более общей проблемы, решением которой занимается шаблон «Адаптер»: стыковка несовместимых интерфейсов. Для организации работы квадратов с окружностями, мне нужна небольшая группа классов и интерфейсов для того, чтоб реализовать шаблон “Адаптер”, как это показано в Листинге 1:
Листинг 1. Квадраты и окружности в Java
public class SquarePeg {
private int width;
public SquarePeg(int width) {
this.width = width;
}
public int getWidth() {
return width;
}
}
public interface Circularity {
public double getRadius();
}
public class RoundPeg implements Circularity {
private double radius;
public double getRadius() {
return radius;
}
public RoundPeg(int radius) {
this.radius = radius;
}
}
public class RoundHole {
private double radius;
public RoundHole(double radius) {
this.radius = radius;
}
public boolean pegFits(Circularity peg) {
return peg.getRadius() <= radius;
}
}
Для того, чтобы уменьшить объем кода Java, Я добавил интерфейс Circularity, обознающий, что реализация имеет радиус. Это позволяет мне написать RoundHole в терминах круглых вещей, а не только RoundPegs. Это распространенная уступка для того, чтобы сделать более простое преобразование типов в шаблоне «Адаптер».
Для того, чтоб помещат квдарты в окружности, мне нужен адаптер, который добавит интерфейс Circularity в класс SquarePegs, реализуя публичный метод getRadius(), как показано в Листинге 2:
Листинг 2. «Адаптер» для квадратов
public class SquarePegAdaptor implements Circularity {
private SquarePeg peg;
public SquarePegAdaptor(SquarePeg peg) {
this.peg = peg;
}
public double getRadius() {
return Math.sqrt(Math.pow((peg.getWidth()/2), 2) * 2);
}
}
Для того, чтобы протестировать действительно ли мой адаптер позволяет помещать квадраты в окружности, я реализую тестовый класс, как показано в Листинге 3:
Листинг 3: Тестирование адаптера
@Test
public void square_pegs_in_round_holes() {
RoundHole hole = new RoundHole(4.0);
Circularity peg;
for (int i = 3; i <= 10; i++) {
peg = new SquarePegAdaptor(new SquarePeg(i));
if (i < 6)
assertTrue(hole.pegFits(peg));
else
assertFalse(hole.pegFits(peg));
}
}
В листинге 3, для каждой предложенной ширины, я делаю обертку SquarePegsAdaptor вокруг создания класса SquarePeg, включая метода pegFits() для того, чтобы получить интеллектуальную оценку, помещается ли мой квадрат в окружность.
Этот код прямолинеен, потому что он прост хотя и использует шаблоны. Эта парадигма — чистый подход в стиле GoF. Тем ни менее, это не единственный возможный подход.
Динамический адаптер в Groovy
Groovy поддерживает несколько парадигм программирования, которых нет в Java, поэтому я буду использовать его для оставшихся примеров. Во-первых, я реализую решение “стандартного” шаблона «Адаптер» из Листинга 2, реализация на Groovy показана в Листинге 4:
Листинг 4: Квадраты, окружности и адаптеры на Groovy
class SquarePeg {
def width
}
class RoundPeg {
def radius
}
class RoundHole {
def radius
def pegFits(peg) {
peg.radius <= radius
}
}
class SquarePegAdapter {
def peg
def getRadius() {
Math.sqrt(((peg.width/2) ** 2)*2)
}
}
Наиболее заметная разница между Java версией и Groovy версией это немногословность. Groovy был реализован так, чтобы убрать повторяемость, присущую Java, с помощью динамической типизации и соглашениями. Например, последняя строка метода служит в качестве возвращаемого значения метода автоматически, как это показано в методе getRadius()
Тест для Groovy версии «Адаптера» представлен в Листинге 5:
Листинг 5. Тестирование традиционного адаптера на Groovy
@Test void pegs_and_holes() {
def hole = new RoundHole(radius:4.0)
(4..7).each { w ->
def peg = new SquarePegAdapter(
peg:new SquarePeg(width:w))
if (w < 6 )
assertTrue hole.pegFits(peg)
else
assertFalse hole.pegFits(peg)
}
}
В Листинге 5, я использовал преимущества другого соглашения Groovy, которое называется “конструктор имя/значение” (name/value constructor), который Groovy формирует автоматически, когда я создаю RoundHole, SquarePegsAdaptor и SquarePeg.
Помимо синтаксического сахара, эта версия так же как и Java версия реализуется в рамках шалонов GoF. Это распространенное явление для Groovy разработчиков, которые перешли из Java программирования и перенесли старый опыт в новый синтаксис. Однако, у Groovy есть более элегантный способ решения этой проблемы, за счет использования метапрограммирования.
Использование метапрограммирования для адаптации
Одна из завораживающих возможностей Groovy это мощная поддержка метапрограммирования. Я буду его использовать для того, чтобы встроить адаптер непосредственно в класс с помощью ExpandoMataClass.
ExpandoMataClass
Общая возможность языков с динамической типизацией это “открытые классы ” (open classes): способность переоткрытия классов (как ваших так и системных, типа String или Object) для добавления, удаления или изменения методов. Открытые классы очень часто используются в DSL и для построения гибких интерфейсов. В Groovy есть 2 механизма для работы с открытыми классами: категории (categories) и ExpandoMataClass. Мой пример показывает только работу с синтаксисом ExpandoMetaClass.
ExpandoMataClass позволяет добавлять новые методы в классы или в отдельные экземпляры класса. В случае подстройки интерфейса, мне необходимо добавить «радиальность» (radiusness) в мой SegPeg до того, как я буду проверять или он помещается в окружность, как представлено в Листинге 6:
Листинг 6. Использование ExpandoMataClass для добавления радиуса квадрату
static {
SquarePeg.metaClass.getRadius = { ->
Math.sqrt(((delegate.width/2) ** 2)*2)
}
}
@Test void expando_adapter() {
def hole = new RoundHole(radius:4.0)
(4..7).each { w ->
def peg = new SquarePeg(width:w)
if (w < 6)
assertTrue hole.pegFits(peg)
else
assertFalse hole.pegFits(peg)
}
}
Каждый класс в Groovy имеет предопределенное свойство metaClass, дающее публичный доступ к ExpandoMetaClass. В Листинге 6, я использую это свойство для того, чтобы добавить метод getRadius(), используя знакомую формулу, в класс SquarePeg. Тут важен тайминг, когда вы используете ExpandoMetaClass; я должен быть уверен что метод добавлен до того, как я пытаюсь его вызвать в юнит-тесте. Таким образом, я добавляю новый метод в статическом инициализаторе тестового класса, который добавляет метод в SquarePegs, когда загружается тестовый класс. После того как метод getRadius() был добавлен в SquarePeg, я могу передать его в метод hole.pegFits, а динамическая типизация Groovy займется всем остальным.
Использование ExpandoMetodClass одназначно более сжато, чем длинное описание шаблона. В то же время оно практические незаметно — что является одним недостатков. Добавление целиком методов в существующие классы должно выполняться бережно, из-за того что вы обмениваете удобство на невидимое поведение, которое может быть трудно отлаживать. Это приемлимо для некоторых классов, как DSLы и глубокие изменения в существующей инфраструктуре фреймворков.
Этот пример показывает использование парадигмы метарограммирования — изменения существующих классов — для решения проблемы адаптера. Тем не менее, это не единственный способ решения проблемы предоставляемый динамическими возможностями Groovy.
Динамические адаптеры
Groovy оптимизирован для удобной интеграции с Java, включая места, где Java отсносительно негибкая. Например, динамическая генерация классов в Java может быть обременительной, но легко решается в Groovy. Это значит, что я могу сгенерировать класс адаптера на лету, как это показано в Листинге 7:
Листинг 7. Использование динамических адаптеров
def roundPegOf(squarePeg) {
[getRadius:{Math.sqrt(
((squarePeg.width/2) ** 2)*2)}] as RoundThing
}
@Test void functional_adaptor() {
def hole = new RoundHole(radius:4.0)
(4..7).each { w ->
def peg = roundPegOf(new SquarePeg(width:w))
if (w < 6)
assertTrue hole.pegFits(peg)
else
assertFalse hole.pegFits(peg)
}
}
Буквенный хэш синтаксис Groovy использует квадратные скобки, которые попадаются в методе roundPegOf() в листинге 7. Для того, чтоб сгенерировать класс, который реализует интерфейс, Groovy дает возможность создать hash, c помощью метода, название которого это ключ, а реализация в виде блоков кода — значения. Оператор as использует хэш для того, чтобы сконструировать класс, который будет реализовывать необходимый интерфейс. Использует ключи хэша для генерации методов.Таким образом, в Листинге 7, метод roundPegOf() создает хэш с одной записью, методом с именем getRadius (ключи хэша Groovy не требуют кавычки, если они являются строками) и мой знакомый код преобразования как реализация метода. Оператор as преобразовывает это все в класс, который реализует интерфейс RoundThing. Данный класс ведет себя как адаптер поверх SquarePeg внутри теста functional_adaptor()
Эта возможность генерировать классы на лету, убирает большую часть формальностей и многословия, в сравнении с традиционными шаблонами проектирования, она также более ясная, чем метапрограммирование. Я не добавляю методы в класс, я генерирую just-in-time обертку для реализации возможностей адаптера. Этот подход использует парадигму шаблонов (добавления класса адаптера), но с минимальными усилиями и емким кодом.
Функциональные адаптеры
Когда у вас есть молоток, любая проблема выглядит как гвоздь. Если вы ориентированы только на объектную парадигму, вы можете не увидеть альтернативных возможностей. Одна из опастностей длительного времяпрепровождения в языках без функций высшего порядка — перегрузка приложения шаблонами для решения проблем. В языках, где отсутствуют функции высшего порядка, много шаблонов (для примера Наблюдатель, Посетитель, Команда ) находится в сердце механизмов организации переносимого кода. Я могу опустить довольно много объектного кода и просто написать функцию, которая будет осуществлять преобразование. И так вышло, что этот подход имеет ряд преимуществ.
Функции!
Если у вас есть функции высшего порядка (функции, которые могут встречаться там же где и конструкции других языков, включая внешние классы), вы можете написать функцию преобразования, которая выполняет адаптацию для вас, как это показано в Листинге 8:
Листинг 8. Использование простой функции преобразования
def pegFits(peg, hole) {
Math.sqrt(((peg.width/2) ** 2)*2) <= hole.radius
}
@Test void functional_all_the_way() {
def hole = new RoundHole(radius:4.0)
(4..7).each { w ->
def peg = new SquarePeg(width:w)
if (w < 6)
assertTrue pegFits(peg, hole)
else
assertFalse pegFits(peg, hole)
}
}
В Листинге 8, я создал функцию которая принимает peg и hole и спользует их для того, чтобы проверить помещается ли peg в отверстие. Данный подход работает, но убирает решение о соответствии из отверстия, где согласно объектной модели он должен быть. В некоторых случаях, имеет смысл вынести отдельно это решение вместо изменения класса.Это подход представляет функциональную парадигму: чистые (pure) функции, которые принимают параметры и возрващают результаты.
Композиция(composition)
До того как закончить с функциональным подходом, я представлю мой любимый адаптер, который объединяет в себе шаблонный и функциональный подходы. Для того, чтобы показать преимущества использования облегченных динамических генераторов(lightweight dynamic adapters) реализуемых функциями высшего порядка, рассмотрим пример в Листинге 9:
(прим. перев: имеется ввиду function composition)
Листинг 9. Композиция функций с помощью облегченных динамических адаптеров (lightweight dynamic adapters)
class CubeThing {
def x, y, z
}
def asSquare(peg) {
[getWidth:{peg.x}] as SquarePeg
}
def asRound(peg) {
[getRadius:{Math.sqrt(
((peg.width/2) ** 2)*2)}] as RoundThing
}
@Test void mixed_functional_composition() {
def hole = new RoundHole(radius:4.0)
(4..7).each { w ->
def cube = new CubeThing(x:w)
if (w < 6)
assertTrue hole.pegFits(asRound(asSquare(cube)))
else
assertFalse hole.pegFits(asRound(asSquare(cube)))
}
}
В Листинге 9, я создал небольшие функции, которые возвращают динамические адаптеры, позволяющие сцеплять адаптеры вместе удобным, читаемым способом. Композиция функций — позволяет функциям контролировать и инкапсулировать то, что происходит с ее параметрами, без заботы о возможном использовании самих функий в качестве параметра. Это довольно функциональный подход, использующий возможность Groovy создавать динамические классы-обертки в качестве реализации.
Сравните решение с помощью облегченного динамического адаптера и неуклюжую композицию адаптеров в библотеках ввода/вывода в Java, показанную в Листинге 10:
Листинг 10. Неуклюжая композиция адаптеров
ZipInputStream zis =
new ZipInputStream(
new BufferedInputStream(
new FileInputStream(argv[0])));
Пример в Листинге 10 показывает распространенную для адаптеров проблему: возможность смешивать и сочетать поведение. Так как в Java нет функций высшего порядка, она вынуждена осуществлять композицию с помощью конструкторов. Использование функций для обертки других функций и модифицирования возвращаемых значений распространено в ФП.Однако, не в Java, поэтому язык добавляет шум в виде чрезмерного синтаксиса.
Заключение
Если вы остаетесь загнанным в рамки одной парадигмы, становится довольно тяжело увидеть преимущества альтернативных подходов, потому что они не укладываются в рамки вашего восприятия. Современные языки со смешением парадигм, предоставляют вам пилитру варинтов проектирования, и понимание того как каждая парадигма работает (и взаимодействует с другими) помогает выбрать вам лучшее решение. В этой части, я показал распространенную проблему стыковки классов и показал традиционные решения на Java и Groovy. Затем, решил проблему с помощью метапрограммирование Groovy и ExpandoMetaClass, а затем показал динамические адаптеры. Вы также увидели, что использование облегченного синтаксиса для классов адаптера позволяет осуществить удобное составление функций, что необычно для Java.
В следующей части, я продолжу исследование шаблонов проектирования и функционального программирования.
Автор: Sigrlami






