Автоматическая расстановка поисковых тегов

В этой статье мы попытаемся рассказать о проблеме множественной классификации на примере решения задачи автоматической расстановки поисковых тегов для текстовых документов в нашем проекте www.favoraim.com. Хорошо знакомые с предметом читатели скорее всего не найдут для себя ничего нового, однако в процессе решения этой задачи мы перечитали много различной литературы где о проблеме множественной классификации говорилось очень мало, либо не говорилось вообще.

Итак, начнем с постановки задачи классификации. Пусть X — множество описаний объектов, Y — множество номеров (или наименований) классов. Существует неизвестная целевая зависимость — отображение y^*:X→Y, значения которой известны только на объектах конечной обучающей выборки X^m={(x_1,y_1 ),…,(x_m,y_m )}. Требуется построить алгоритм a:X→Y, способный классифицировать произвольный объект x∈X. Однако более распространенным является вероятностная постановка задачи. Пусть X — множество описаний объектов, Y — множество номеров (или наименований) классов. На множестве пар «объект, класс» X×Y определена вероятностная мера P. Имеется конечная обучающая выборка независимых наблюдений X^m={(x_1,y_1 ),…,(x_m,y_m )}, полученных согласно вероятностной мере P.

Теперь перейдем к задаче автоматической расстановки поисковых тегов. У нас имеется объект x – текстовый документ и множество классов Y= {y_i },i=(1,N) ̅ – поисковых тегов. Каждому документу нужно поставить в соответствие один или несколько поисковых тегов. Например у нас есть событие с заголовком «Концерт группы Apocalyptica», данному событию можно присвоить следующие поисковые теги: «Apocalyptica», «концерт», «heavy metal», «виолончель» и т.п. Также у нас имеется обучающая выборка, т.е. набор документов с уже расставленными поисковыми тегами. Таким образом, у нас есть задача классификации с пересекающимися классами, т.е. объект может относиться одновременно к нескольким классам. Но вместо этого мы будем решать N задач бинарной классификации, каждую пару (x,y_i ) i=(1,N) ̅ классифицируем на классы {0,1}, т.е. определяем, можно ли поставить поисковый тег y_i документу x или нет.
Для решения данной задачи мы будем представлять текстовые документы в виде «bag of words» или многомерного вектора слов и их веса (частота встречаемости) в документе (http://en.wikipedia.org/wiki/Bag-of-words_model). На рис. 1 показана гистограмма слов описания бизнес-тренинга, на рис. 2 – гистограмма слов описания мастер-класса по фотографии.

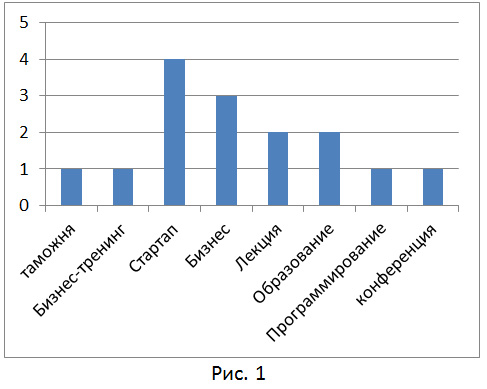
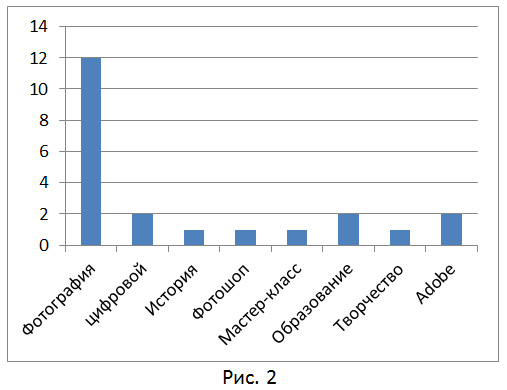
В качестве метода классификации можно взять любой статистический (Байесовский) метод классификации. Вероятностная модель для классификатора — это условная модель p(y│d),y∈Y. Теперь нам нужно восстановить плотность p(y│d),y∈Y, т.е. вероятность того, что для нашего документа d можно поставить поисковый тег y∈Y. Для восстановления плотности существует множество методов, начать можно с наивной байесовской модели классификации документов (http://ru.wikipedia.org/wiki/Классификация_документов). Для этой модели делается «наивное» предположение о независимости встречающихся в документе слов, и, хотя это очевидно неверное предположение, модель работает достаточно неплохо.
Теперь, когда мы восстановили плотность распределения и для каждого тега y∈Y нашли вероятность того, что его можно присвоить нашему документу d, нужно определить, какие из тегов нужно присвоить документу, а какие отбросить, т.е. найти минимальный отсекающий порог для вероятности p(y│d). Тут придется воспользоваться анализом ROC-кривой (http://www.machinelearning.ru/wiki/index.php?title=ROC-кривая).
ROC-кривая показывает зависимость количества верно классифицированных положительных примеров (true positive rate) от количества неверно классифицированных отрицательных примеров (false positive rate). При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения. В нашем случае, в роли данного параметра будет выступать вероятность p(y│d). Строится ROC-кривая по контрольной выборке, которая обычно является частью обучающей выборки. При этом объекты контрольной выборки нельзя использовать для обучения классификатора, в противном случае мы можем получить излишне-оптимистичную ROC-кривую вследствие явления переобучения. Однако, если нам позволяют ресурсы, мы можем воспользоваться перекрестной проверкой (cross-validation). Суть ее заключается в том, что обучающая выборка разбивается на k частей, k-1 из которых используются для обучения модели, оставшаяся же часть используется в качестве контрольной выборки. Данная процедура выполняется k раз. На практике использовать данный прием проблематично, т.к. вычисления занимают очень много времени.

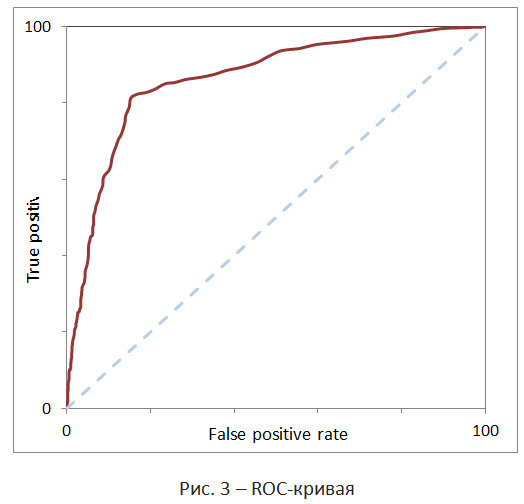
ROC-кривая обладает следующими основными характеристиками. Чувствительность (sensitivity) – это и есть доля истинно положительных случаев. Специфичность (specificity) – доля истинно отрицательных случаев, которые были правильно идентифицированы моделью. Заметим, что fpr=100-specifity. Площадь под ROC-кривой (AUC). Значение AUC обычно используют для оценки качества классификатора. Например, зависимость fpr=tpr соответствует худшему случаю (случайное гадание). На рис. 3 худший случай обозначен пунктирной линией. Чем выше плотность, тем более качественные предсказания дает классификатор. Для идеального классификатора график ROC-кривой проходит через верхний левый угол.
Теперь нужно выбрать минимальный отсекающий порог. Тут существует 3 подхода.
Требование минимальной величины чувствительности (специфичности) модели. Т.е. одно из значений задается константно и, исходя из этого, подбирается значение отсекающего порога.
Требование максимальной суммарной чувствительности и специфичности модели.
Требование баланса между чувствительностью и специфичностью, т.е. когда specificity≈sensivity. Тут порог – это точка пересечения двух кривых, когда по оси x откладывается порог отсечения, а по оси y – чувствительность и специфичность модели (рис. 4).

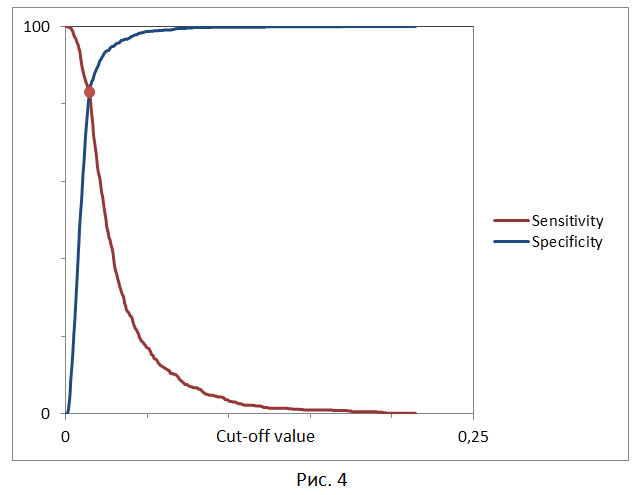
Таким образом, мы можем присвоить нашему документу d те поисковые теги, для которых выполняется p(y│d)>c, где c – значение порога отсечения.

Автор: favoraim

Источник