Как вы уже давно привыкли, график вещественной функции в математике — некая кривая, которая показывает, как ведёт себя функция при изменении её аргумента. Иногда эта кривая может быть весьма красива, особенно, если речь идёт о графиках некоторых уравнений, как, например, этого.
Но в данном посте речь пойдёт о функции двух вещественных аргументов. И возвращать эта функция будет не число, а оттенок цвета. Да-да, значение от 0 до 255, которое будет зависеть от положения точки, то есть от двух её координат (раз уж мы собрались делать плоский рисунок). Кто до сих пор слабо представляет, о чем идёт речь, объясню на примере. Вот график функции cos(x*y):

Что можно сказать, глядя на этот график? Ну во-первых, что функция наша в каком-то роде периодична. Во-вторых, на первом промежутке монотонности она убывает. Ну действительно: при движении от левой верхней точки рисунка вправо или вниз, цвет становится более тёмным, то есть, значение функции стремится к нулю. А теперь, друзья, пришла пора развлекаться. Погнали.
Поскольку всё это легко реализуется с помощью в двойном цикле, то можно очень быстро сварганить небольшую программку, где пользователь выбирает функцию для каждого из RGB каналов и числовые параметры (перед x,y и самой f(x)), нажимает кнопку «построить график» и наслаждается. Я выбрал delphi в качестве среды, поскольку там наиболее удобно (на мой взгляд) работать с графикой.
Помещаем на формочку компонент Timage, пишем саму функцию
function f_red(x,y): byte
{
result:=k1*round(sin(k2*x*y));
}
Или, к примеру, что-нибудь более сложное типа
function f_red(x,y): byte
{
result:=k1*round(arcctg(k2*x*(y+k1))+random(x*20)/log(k2*x,y));
}
Ну и OnClick event для кнопочки:
for x:=0 to width do
for y:=0 to height do
image1.canvas.pixels[x,y]:=RGB(f_red(x,y), f_green(x,y), f_blue(x,y));
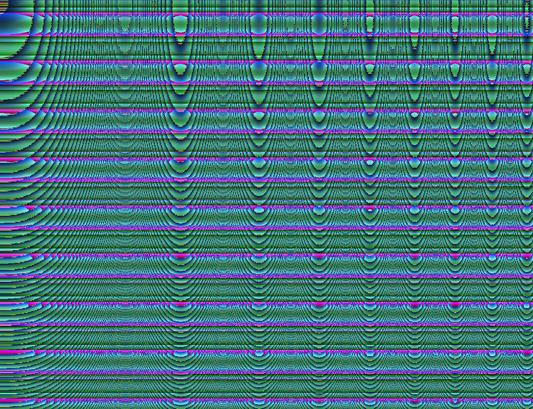
Конечно, можно поэкспериментировать со смешиванием, выходом значения за пределы от 0 до 255… тут, как говорится, на что фантазии хватит. В качестве outro просто покажу то, что вышло у меня:




Автор: mr_salik




