 Однажды я столкнулся с задачей генерации 128-битных случайных чисел для реализации генетического алгоритма. Из-за большой размерности задачи алгоритм гонялся долго, поэтому были повышенные требования к скорости работы. Я решил написать свой генератор специально для поставленной задачи.
Однажды я столкнулся с задачей генерации 128-битных случайных чисел для реализации генетического алгоритма. Из-за большой размерности задачи алгоритм гонялся долго, поэтому были повышенные требования к скорости работы. Я решил написать свой генератор специально для поставленной задачи.
В этом посте речь пойдет о применении линейного конгруэнтного метода для получения псевдослучайных чисел разрядности 64 и 128 бит с пояснением принципа работы и подбора параметров.
Если вам в тягость пользоваться ГСЧ из стандартной библиотеки, у вас к нему нестандартные требования или просто охота держать под контролем весь процесс генерации случайных чисел в своем приложении, добро пожаловать под кат.
Долой стандартный генератор!
Многим известно, что генерация случайных чисел является неотъемлемой частью многих алгоритмов. Кроме математики и статистики случайные числа используются в методах компьютерного моделирования, криптографии, машинного обучения (искусственные нейронные сети), стохастической оптимизации (эволюционные вычисления) и во многих задачах из других сфер, например, в более понятных вещах вроде рендера красивых картинок, работе движков и логики видеоигр.
Все достаточно распространенные языки программирования имеют функции для генерации случайных (или, если быть предельно точным, псевдослучайных) чисел. Однако иногда возникает необходимость реализовать свой собственный генератор случайных чисел (ГСЧ). Хотя ГСЧ «из коробки» обычно достаточно хорош для применения в большинстве случаев, но бывает и так, что слишком крутой генератор вроде бы и не нужен, но встроенный ГСЧ все равно не нравится.
Причины могут быть разные и неочевидные на первый взгляд. Во-первых, стоит отметить, что проблема генерации случайных чисел зачастую включает в себя поиск баланса между скоростью работы и качеством результата. Иногда нужно сделать чуть быстрее или чуть сложнее.
Во-вторых, ГСЧ – не просто каша из арифметических операций, а строго детерминированный алгоритм, характеристики которого могут сильно варьироваться. В некоторых научных экспериментах необходимо полностью описывать условия тестов для гарантии возможности их воспроизведения. Сюда относятся алгоритм и параметры ГСЧ. В этом случае лучше иметь свою реализацию.
Может возникнуть задача, в которой необходима одновременная работа разных ГСЧ. Именно разных, а встроенный генератор обычно один. Можно, конечно, запустить несколько копий с различным начальным зерном, однако в этом случае генераторы будут выдавать элементы одной и той же последовательности (которая циклически повторяется) просто начав из разных мест. Длина цикла огромна, но теоретически это может создать проблемы.
В моем случае нужно было генерировать 128-разрядные числа. В C++ нет функции, которая возвращала хотя бы 64-битные. После продолжительного гугления я обнаружил путаницу в rand() и RAND_MAX в разных компиляторах, набор костылей для генерации 64 бит, и решил отказаться от встроенного ГСЧ. Написание своего генератора показалось мне элементарной задачей – за пару итераций линейного конгруэнтного генератора получить два 64-разрядных числа, а затем склеить их. Это оказалось не так просто. Но обо всем по порядку.
За дело!
Итак, приступим к созданию ГСЧ. За основу возьмем простой и популярный линейный конгруэнтный метод, который работает по формуле:
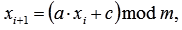
где xi, xi+1 – текущее и следующее случайные числа; a, c и m – некоторые константы; mod – оператор нахождения остатка от деления.
Константу m часто берут равной 232 или 264 дабы избежать деления в программной реализации. Чтобы в результате получались 64-битные остатки, я использовал m=264. Но где же взять константы a и c? В Википедии была найдена следующая пара: a=6364136223846793005 и c=1442695040888963407. Недолго думая, я написал генератор, использующий эти параметры, и начал тестировать свой генетический алгоритм. Однако он быстро зацикливался. Подозрения пали на ГСЧ. Оказывается, несколько младших разрядов у полученной последовательности 64-битных «случайных» чисел демонстрировали отнюдь не случайное поведение. Значения некоторых двоичных разрядов подряд идущих чисел изображены в виде монохромных картинок:


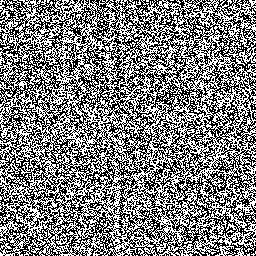
Значения младших 5-го, 15-го и 20-го разрядов (нумерация с нуля)
Примерно 20-24 младших двоичных разряда оказываются не пригодны для использования. С увеличением номера разряда повышается его случайность. Таким образом, чтобы получить одно 64-битное случайное число, необходимы две итерации линейного конгруэнтного генератора. Результат получается конкатенацией двух 32-битных фрагментов:
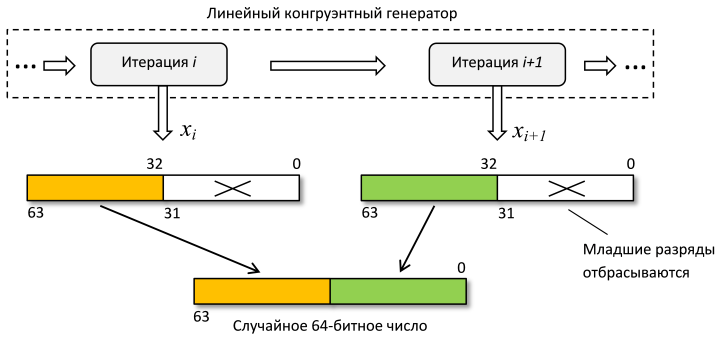
Например, в java.util.Random используется такой же принцип, хотя из-за того, что m=248, там отбрасываются только 16 младших разрядов при генерации int и long. Это, разумеется, отрицательно влияет на качество случайных чисел.
Вот пример последовательности 64-битных чисел, которая получается при a=6364136223846793005, c=1442695040888963407, m=264, x0=0 описанным на рисунке способом:
1442695037175000593
11166244415259155177
7076646891078057782
1459328390042580878
8905969149530007863
11682375496967736740
897247724006084730
Насколько случайны эти числа? Примерно на уровне ГСЧ из стандартной библиотеки Java, возможно даже чуть лучше. Расчет каждого числа требует всего две операции умножения.
Если нужны несколько разных генераторов, следует выбрать другие значения констант a и c, рассчитанные на m=264. В статье по этой ссылке приведены примеры трех констант с «хорошими качествами»:
| a = 2862933555777941757 | c – нечетное, m=264 |
| a = 3202034522624059733 | |
| a = 3935559000370003845 |
128-битные случайные числа
Нет ничего сложного в том, чтобы слепить два 64-разрядных числа в одно, тем не менее, здесь есть один интересный момент: одновременная генерация двух чисел по 64 разряда может быть на 25% быстрее, чем последовательная, при незначительном ущербе для их «случайности».
Идея состоит в том, чтобы обойтись тремя итерациями линейного конгруэнтного генератора вместо необходимых четырех. Этого можно добиться, если отбрасывать только 20 младших бит от результата на каждой итерации вместо 32-х как в предыдущем методе. Как можно видеть на монохромной картинке выше, 20-й разряд уже достаточно случаен, чтобы быть использованным. Оставшиеся разряды позволяют сформировать 128-битное число.

class RandomGenerator
{
public:
RandomGenerator(unsigned long long int seed = 0);
void next(unsigned long long int *hi, unsigned long long int * lo);
private:
unsigned long long int currentSeed;
};
RandomGenerator::RandomGenerator(unsigned long long int seed) :
currentSeed(seed)
{}
void RandomGenerator::next(unsigned long long int *hi, unsigned long long int *lo)
{
const unsigned long long int a = 6364136223846793005;
const unsigned long long int c = 1442695040888963407;
const unsigned long long int x = a * this->currentSeed + c;
const unsigned long long int y = a * x + c;
const unsigned long long int z = a * y + c;
*hi = (x & 0xfffffffffff00000) | (z >> 44);
*lo = (y & 0xfffffffffff00000) | ((z >> 24) & 0xfffff);
this->currentSeed = z;
}
Используя те же параметры a, c, m и x0, получаются такие числа:
26613026195691280501944396807868523054
136526799440480448897747671965175330512
26919857327062567305005081067174740455
151962490054994640693408155996993201355
16551299175504952598134597160493279376
67275013191410065527820230898073478166
72445587156806476974393951227561270647
Этого способа добычи случайных чисел оказалось достаточно, чтобы мое приложение заработало. Получилось быстро и практично. Наверняка информация из статьи кому-нибудь окажется полезной. На этом все, спасибо за внимание. (Картинка с кубиками на обложке взята отсюда.)
Всем счастливых случайностей в новом году!
Автор: Insty






