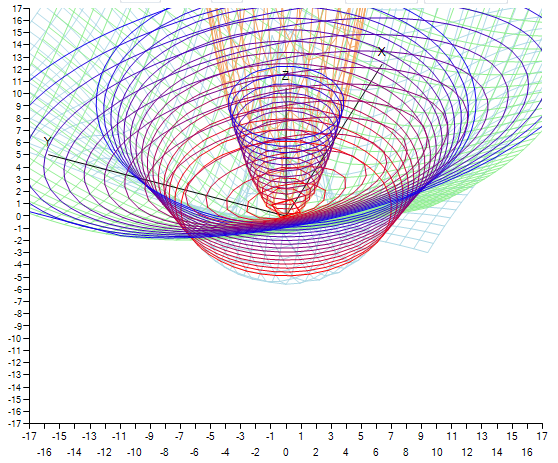
Статья представляет собой нечто вроде “практического руководства” для построения весьма интересных трехмерных графиков функций вида z=f(x,y), с примером реализации на C#.
Рисовать будем в компоненте Chart, разумеется, можно использовать любой canvas-подобный элемент. При большом количестве точек будут наблюдаться задержки в рисовании, но этот компонент легко использовать и для демонстрации он вполне сгодится.
Строим график
Для этого нам понадобится сетка или поле, каждый узел которой будет иметь координаты x, y и содержать значение z. Эту сетку можно заполнять любым способом, раз мы строим график функции, то будем заполнять ее значениями этой функции (z=f(x,y)). Шаг между двумя последовательными значениями x или y выберем равный одному, для более простой и наглядной демонстрации, размерность сетки N x N. Значения в узлах сетки достаточно считать один раз. Для преобразования трехмерных координат в двухмерные и для поворота графика будем использовать матрицу поворота и углы Эйлера.
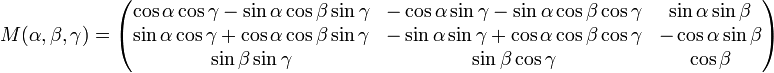
Обозначим углы α, β и γ углами a, b и c соответственно и будем использовать их значения в градусах. Запишем матрицу через коэффициенты:
| l1, l2, l3 | M=| m1, m2, m3 | | n1, n2, n3 | l1 = cos(a) * cos(c) - cos(b) * sin(a) * sin(c) m1 = sin(a) * cos(c) + cos(b) * cos(a) * sin(c) n1 = sin(b) * sin(c) l2 = -cos(a) * sin(c) + cos(b) * sin(a) * cos(c) m2 = -sin(a) * sin(c) + cos(b) * cos(a) * cos(c) n2 = sin(b) * cos(c) l3 = sin(b) * sin(a) m3 = -sin(b) * cos(a) n3 = cos(b)
Запишем итоговое преобразование из трехмерных координат в двухмерные:
X=l1x+l2y+l3z
Y=m1x+m2y+m3z
x,y,z –это “внутренние” координаты для графика, X,Y – итоговые экранные координаты. Коэффициенты n1,n2 и n3 нам для этой задачи не понадобятся.
double[,] a; //массив размерностью N x N
…
double X, Y;
//Рисуем вертикальные линии при постоянном значении x
for (int x = 0; x < N; x++)
{
for (int y = 0; y < N; y++)
{
X = l1() * (x - N / 2.0) + l2() * (y - N / 2.0) + l3() * a[x, y];
Y = m1() * (x - N / 2.0) + m2() * (y - N / 2.0) + m3() * a[x, y];
chart1.Series[n].Points.AddXY(X, Y);
}
n++;
}
//Рисуем горизонтальные линии при постоянном значении y
for (int y = 0; y < N; y++)
{
for (int x = 0; x < N; x++)
{
X = l1() * (x - N / 2.0) + l2() * (y - N / 2.0) + l3() * a[x, y];
Y = m1() * (x - N / 2.0) + m2() * (y - N / 2.0) + m3() * a[x, y];
chart1.Series[n].Points.AddXY(X, Y);
}
n++;
}
Добавим события, при которых будут меняться углы и будет происходить вращение графика. Например, это будет движение курсора при зажатой левой кнопке мышки и изменение углов b и с:
bool onmove = false;
Point startpos;
…
private void chart1_MouseDown(object sender, MouseEventArgs e)
{
if (e.Button == MouseButtons.Left)
{
onmove = true;
startpos = e.Location;
}
}
private void chart1_MouseMove(object sender, MouseEventArgs e)
{
if (onmove)
{
if ((startpos.Y - e.Y) < 0) b--;
if ((startpos.Y - e.Y) > 0) b++;
if ((startpos.X - e.X) < 0) c--;
if ((startpos.X - e.X) > 0) c++;
if (b > 359) b = 0;
if (c > 359) c = 0;
if (b < 0) b = 359;
if (c < 0) c = 359;
drawscene();
}
}
private void chart1_MouseUp(object sender, MouseEventArgs e)
{
if (e.Button == MouseButtons.Left) onmove = false;
}
Проверим на тестовой функции z=x2+y2:

Вид сверху на функцию где видно ту самую сетку и показаны значения в узлах.
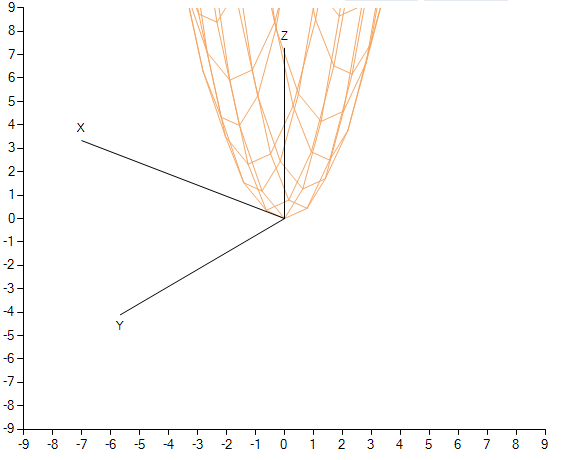
Вид на функцию под углом.
Возможно, стоит по-другому изменять углы, при вращении используя все 3 угла и использовать сетку с шагом меньше 1, но мы упростили ситуацию.
Строим изолинии
Воспользуемся алгоритмом Движущихся квадратов (“Marching squares”), в Википедии дано достаточно подробное описание. Гугл также выдает очень хорошую статью, где описывается этот алгоритм и реализовывается на C#.
Суть кратко:
1. Требуется найти начальную позицию — откуда пойдет изолиния.
2. Затем сравнить значения в соседних узлах сетки, которые образуют квадрат с вершинами: (xi,yj), (xi-1,yj), (xi,yj-1), (xi-1,yj-1).
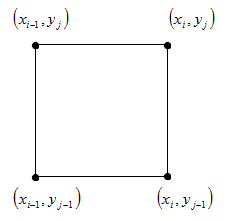
3. Выбрать дальнейшее направление обхода, в зависимости от полученного значения на шаге 2, и перейти в следующую точку, в которой опять проделать шаг 2.
4. Выполнять до тех пор, пока не попадем обратно в начальную позицию или не достигнем края сетки.
Всего может быть 16 вариантов:
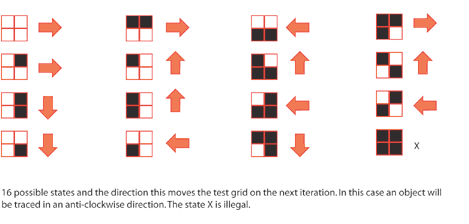
Не будем писать весь код заново, возьмем часть кода из той статьи и изменим под нашу задачу:
enum dir
{
None,
Up,
Left,
Down,
Right
}
dir prevStep;
dir nextStep;
bool border;
int startx, starty;
void findstartpos()
{
for (int y = 0; y < N; y++)
for (int x = 0; x < N; x++)
if (arr[x, y] < Z)
{
startx = x;
starty = y;
return;
}
}
bool check(int x, int y)
{
if (x == N - 1 || y == N - 1 || x == 0 || y == 0) border = true;
if (x < 0 || y < 0 || x >= N || y >= N) return false;
if (arr[x, y] < Z) return true;
return false;
}
void step(int x, int y)
{
bool ul = check(x - 1, y - 1);
bool ur = check(x, y - 1);
bool dl = check(x - 1, y);
bool dr = check(x, y);
prevStep = nextStep;
int state = 0;
if (ul) state |= 1;
if (ur) state |= 2;
if (dl) state |= 4;
if (dr) state |= 8;
switch (state)
{
case 1: nextStep = dir.Down; break;
case 2: nextStep = dir.Right; break;
case 3: nextStep = dir.Right; break;
case 4: nextStep = dir.Left; break;
case 5: nextStep = dir.Down; break;
case 6:
if (prevStep == dir.Down)
{
nextStep = dir.Left;
}
else
{
nextStep = dir.Right;
}
break;
case 7: nextStep = dir.Right; break;
case 8: nextStep = dir.Up; break;
case 9:
if (prevStep == dir.Right)
{
nextStep = dir.Down;
}
else
{
nextStep = dir.Up;
}
break;
case 10: nextStep = dir.Up; break;
case 11: nextStep = dir.Up; break;
case 12: nextStep = dir.Left; break;
case 13: nextStep = dir.Down; break;
case 14: nextStep = dir.Left; break;
default:
nextStep = dir.None;
break;
}
}
Попробуем опять же на нашей тестовой функции z=x2+y2:
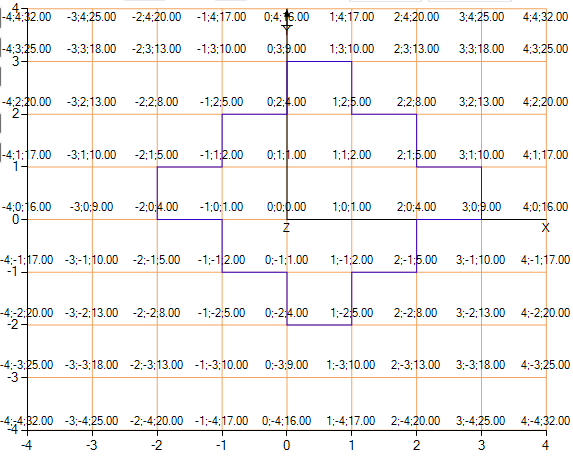
Как видно на картинке алгоритм довольно успешно справился и отделил точки где значение функции выше 5, но немного правее и выше. Изолиния получилась угловатой, поэтому проведем интерполяцию. Смысл интерполяции в том, что мы на основании значениях z в соседних узлах сетки вычисляем более близкое значение x, или y, к реальной изолинии, что делает изолинию более правдоподобной.
Будем использовать формулу линейной интерполяции:
x=(Z-f(xi-1,yj)/(f(xi,yj)-f(xi-1,yj))+xi-1,
y=(Z-f(xi,yj-1)/(f(xi,yj)-f(xi,yj-1))+yj-1,
где Z- значение, на котором нужно провести изолинию.
Интерполирование по координате x, или по координате y, выбирается в зависимости от направления движения для предыдущего и следующего шагов.
Напишем для этого такой, не очень хороший код:
...
List<PointF> res;
...
//Изменение координаты x или y
int dx = 0, dy = 0;
switch (prevStep)
{
case dir.Down: dy = 1; break;
case dir.Left: dx = 1;break;
case dir.Up: dy = -1; break;
case dir.Right: dx = -1; break;
default: break;
}
...
double X = x0 + x;
double Y = y0 + y;
if (ip) //ip - interpolation
{
//Интерполируем при неизменном направлении
if (dx != 0 && prevStep == nextStep)
Y = y0 + y + (Z - a[x, y - 1]) / (a[x, y] - a[x, y - 1]) - 1;
if (dy != 0 && prevStep == nextStep)
X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1;
//Интерполируем при изменении направления
if (nextStep == dir.Down && prevStep == dir.Left)
Y = y0 + y + (Z - a[x, y - 1]) / (a[x, y] - a[x, y - 1]) - 1;
if (nextStep == dir.Left && prevStep == dir.Down)
X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1;
if (nextStep == dir.Up && prevStep == dir.Right)
X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1;
if (nextStep == dir.Up && prevStep == dir.Left)
X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1;
if (nextStep == dir.Right && prevStep == dir.Up)
Y = y0 + y + (Z - a[x, y - 1]) / (a[x, y] - a[x, y - 1]) - 1;
if (nextStep == dir.Right && prevStep == dir.Down)
X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1;
//Исключаем "ненужные" точки
if (!(nextStep == dir.Down && prevStep == dir.Right) &&
!(nextStep == dir.Left && prevStep == dir.Up))
res.Add(new PointF((float)X, (float)Y));
}
...
И получаем результат, который нас уже более устраивает:
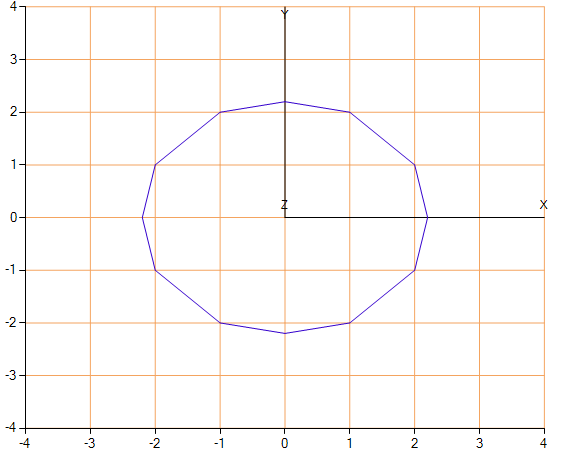

Пример «ненужных точек», которые мы исключили.
Из возможных улучшений следует отметить, что наша реализация будет строить все изолинии только для монотонно возрастающих (для убывающих следует поменять знак на “>”) функций. Для функций периодически возрастающих и убывающих следует изменить, например функцию поиска начальной позиции и выполнять её несколько раз.
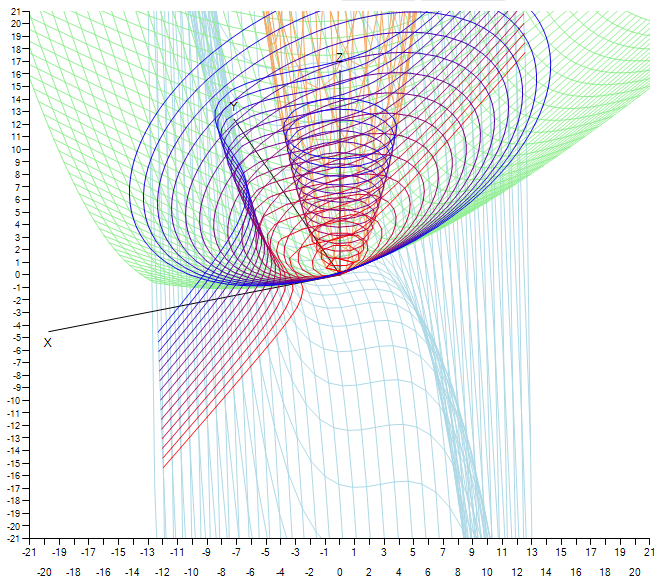
Пример работы итоговой программы.
На практике это можно применять для анализа карт, или для поиска контура на изображении.
Исходный код программы можно скачать тут или тут.
Еще раз ссылки, которые использовались:
ru.wikipedia.org/wiki/Матрица_поворота
ru.wikipedia.org/wiki/Углы_Эйлера
ru.wikipedia.org/wiki/Интерполяция
ru.wikipedia.org/wiki/Marching_squares
devblog.phillipspiess.com/2010/02/23/better-know-an-algorithm-1-marching-squares/
Автор: sobak





