На самом деле, большая доля этих правил не влияет на среду исполнения кода, который вы пишете. Подобные правила невозможно оценить объективно, да это и необязательно, ведь на этом этапе они достаточно произвольны. Однако есть правила «чистого» кода, на которые делают особый упор — это правила, которые можно измерить объективно, поскольку они влияют на поведение кода в среде исполнения.
Если посмотреть на список правил «чистого» кода и вытащить из него правила, которые действительно влияют на структуру кода, то мы получим следующее:
- Отдавайте предпочтение полиморфизму, а не «if/else» и «switch»
- Код не должен знать о внутреннем устройстве объектов, с которыми он работает
- Функции должны быть маленькими
- Каждая функция должна выполнять одну задачу
- Принцип «DRY» — Don’t Repeat Yourself («не повторяйся»)
Эти правила достаточно чётко формулируют то, как должен создаваться конкретный фрагмент кода, чтобы быть «чистым». Но я задам такой вопрос: если мы создадим фрагмент кода, соответствующий этим правилам, какова будет его производительность?
Чтобы создать наиболее предпочтительный пример для реализации чего-то на «чистом» коде, я воспользовался готовыми примерами кода, содержащимися в литературе о «чистом» коде. Таким образом, мне не придётся ничего придумывать, я просто оценю правила защитников «чистого» кода при помощи тех примеров кода, которыми они иллюстрируют эти правила.
В примерах «чистого кода» часто встречаются такие:
<code>/* ========================================================================
LISTING 22
======================================================================== */
class shape_base
{
public:
shape_base() {}
virtual f32 Area() = 0;
};
class square : public shape_base
{
public:
square(f32 SideInit) : Side(SideInit) {}
virtual f32 Area() {return Side*Side;}
private:
f32 Side;
};
class rectangle : public shape_base
{
public:
rectangle(f32 WidthInit, f32 HeightInit) : Width(WidthInit), Height(HeightInit) {}
virtual f32 Area() {return Width*Height;}
private:
f32 Width, Height;
};
class triangle : public shape_base
{
public:
triangle(f32 BaseInit, f32 HeightInit) : Base(BaseInit), Height(HeightInit) {}
virtual f32 Area() {return 0.5f*Base*Height;}
private:
f32 Base, Height;
};
class circle : public shape_base
{
public:
circle(f32 RadiusInit) : Radius(RadiusInit) {}
virtual f32 Area() {return Pi32*Radius*Radius;}
private:
f32 Radius;
};Это базовый класс для фигур, из которого порождается несколько конкретных фигур: круг, треугольник, прямоугольник, квадрат. Далее идёт виртуальная функция, вычисляющая площадь.
Как и требуют правила, мы отдаём предпочтение полиморфизму. Каждая наша функция выполняет только одну задачу. Они компактны. Всё это отлично. Итак, мы получили «чистую» иерархию классов, каждый порождённый класс знает, как вычислять свою площадь и хранит данные, требуемые для вычисления этой площади.
Если мы представим, что используем эту иерархию для выполнения какой-то задачи, допустим, для нахождения общей площади передаваемой серии фигур, то ожидаем увидеть что-то подобное:
/* ========================================================================
LISTING 23
======================================================================== */
f32 TotalAreaVTBL(u32 ShapeCount, shape_base **Shapes)
{
f32 Accum = 0.0f;
for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex)
{
Accum += Shapes[ShapeIndex]->Area();
}
return Accum;
}Я не использовал здесь итератор, потому что в правилах не говорится ничего о том, что нам нужно использовать итераторы. Поэтому я решил, что не буду давать «чистому» коду кредит доверия и не стану добавлять никакого абстрагированного итератора, который может сбить с толку компилятор и привести к снижению производительности.
Вы также можете заметить, что это цикл по массиву указателей. Это прямое последствие использования иерархии классов: мы понятия не имеем, какой размер в памяти может занимать каждая из этих фигур. Так что если мы не собираемся добавлять вызов ещё одной виртуальной функции для получения размера данных каждой фигуры и использовать для их обхода какую-то процедуру пропуска переменных, нам понадобятся указатели, чтобы выяснять, где начинается каждая фигура.
Поскольку это накопление, существует циклически порождаемая зависимость, способная замедлить цикл. Так как порядок накопления может произвольно меняться, я для безопасности также написал разворачиваемую вручную версию:
/* ========================================================================
LISTING 24
======================================================================== */
f32 TotalAreaVTBL4(u32 ShapeCount, shape_base **Shapes)
{
f32 Accum0 = 0.0f;
f32 Accum1 = 0.0f;
f32 Accum2 = 0.0f;
f32 Accum3 = 0.0f;
u32 Count = ShapeCount/4;
while(Count--)
{
Accum0 += Shapes[0]->Area();
Accum1 += Shapes[1]->Area();
Accum2 += Shapes[2]->Area();
Accum3 += Shapes[3]->Area();
Shapes += 4;
}
f32 Result = (Accum0 + Accum1 + Accum2 + Accum3);
return Result;
}Если запустить эти две процедуры в простой тестовой обвязке, то можно приблизительно замерить общее количество тактов на фигуру, требуемое для выполнения этой операции:
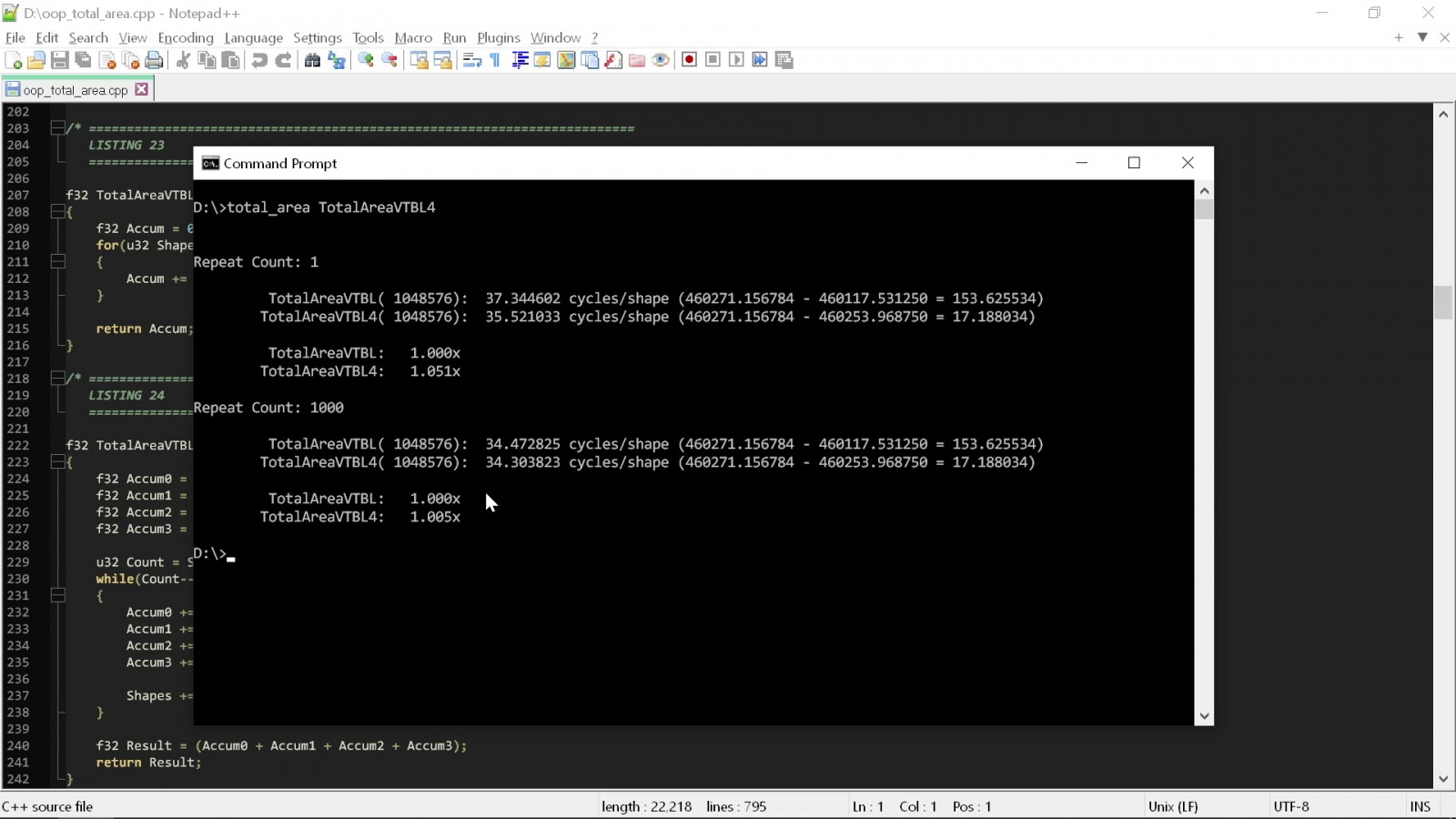
Обвязка хронометрирует код двумя способами. Первый — запустить код только один раз, чтобы показать, что происходит в произвольном «холодном» состоянии — данные должны быть в L3, однако L2 и L1 сброшены, а алгоритм предсказания ветвления ещё не «практиковался» на этом цикле.
Второй способ — многократное выполнение кода, чтобы посмотреть. что происходит, когда кэш и алгоритм предсказания ветвления работают наиболее удобным для цикла образом. Стоит заметить, что оба способа не являются хардкорными измерениями, поскольку, как вы видите, различия настолько велики, что нам не нужно применять какие-то серьёзные инструменты анализа.
Из результата мы видим, что между двумя процедурами нет особой разницы. Для выполнения вычисления площади «чистым» кодом требуется примерно 35 тактов. Если сильно повезёт, это количество иногда снижается до 34.
Итак, 35 тактов — это то значение, которое стоит ожидать получить при следовании всем правилам. Но что же произойдёт, если мы нарушим лишь первое правило? Что, если вместо применения здесь полиморфизма мы просто используем оператор switch? [Лично я не думаю, что оператор switch обязательно менее полиморфический, чем vtable. Это просто две разные реализации одного принципа. Однако правила «чистого» кода приказывают отдавать предпочтение полиморфизму вместо операторов switch, поэтому я использую здесь их терминологию, означающую, что они чётко считают, что оператор switch не полиморфический.]
Ниже я записал точно такой же код, однако вместо использования иерархии классов (а следовательно, vtable в среде исполнения) я написал его при помощи перечисления и типа фигуры, который упрощает всё до одной структуры:
/* ========================================================================
LISTING 25
======================================================================== */
enum shape_type : u32
{
Shape_Square,
Shape_Rectangle,
Shape_Triangle,
Shape_Circle,
Shape_Count,
};
struct shape_union
{
shape_type Type;
f32 Width;
f32 Height;
};
f32 GetAreaSwitch(shape_union Shape)
{
f32 Result = 0.0f;
switch(Shape.Type)
{
case Shape_Square: {Result = Shape.Width*Shape.Width;} break;
case Shape_Rectangle: {Result = Shape.Width*Shape.Height;} break;
case Shape_Triangle: {Result = 0.5f*Shape.Width*Shape.Height;} break;
case Shape_Circle: {Result = Pi32*Shape.Width*Shape.Width;} break;
case Shape_Count: {} break;
}
return Result;
}Это «олдскульный» способ, которым решались бы подобные задачи до появления «чистого» кода.
Обратите внимание, что поскольку у нас больше нет специальных типов данных для каждого варианта фигуры, то если тип не имеет одного из значений (например, «height»), он просто его не использует.
Теперь вместо получения площади от вызова виртуальной функции пользователь этой структуры получает её от функции с оператором switch: именно этого правила «чистого» кода никогда не рекомендуют делать. Несмотря на это, вы заметите, что код, несмотря на гораздо большую краткость, по сути, остался тем же. Каждый case оператора switch — это просто тот же код, что и в соответствующей виртуальной функции в иерархии классов.
Что касается самих циклов суммирования, то можно увидеть, что они практически идентичны «чистой» версии:
/* ========================================================================
LISTING 26
======================================================================== */
f32 TotalAreaSwitch(u32 ShapeCount, shape_union *Shapes)
{
f32 Accum = 0.0f;
for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex)
{
Accum += GetAreaSwitch(Shapes[ShapeIndex]);
}
return Accum;
}
f32 TotalAreaSwitch4(u32 ShapeCount, shape_union *Shapes)
{
f32 Accum0 = 0.0f;
f32 Accum1 = 0.0f;
f32 Accum2 = 0.0f;
f32 Accum3 = 0.0f;
ShapeCount /= 4;
while(ShapeCount--)
{
Accum0 += GetAreaSwitch(Shapes[0]);
Accum1 += GetAreaSwitch(Shapes[1]);
Accum2 += GetAreaSwitch(Shapes[2]);
Accum3 += GetAreaSwitch(Shapes[3]);
Shapes += 4;
}
f32 Result = (Accum0 + Accum1 + Accum2 + Accum3);
return Result;
}Единственное отличие заключается в том, что вместо вызова функции-члена для получения площади мы вызываем обычную функцию, вот и всё.
Однако вы сразу можете увидеть немедленную выгоду от использования упрощённой структуры по сравнению с применением иерархии классов: фигуры могут просто находиться в массиве, без необходимости указателей. Косвенных действий нет, потому что мы сделали все фигуры одного размера.
Плюс мы получаем выигрыш ещё и в том, что теперь компилятор может точно видеть, что происходит в цикле, потому что он может просто смотреть на функцию GetAreaSwitch и видеть весь путь выполнения кода. Ему не нужно предполагать, что нечто может произойти в какой-то виртуализированной функции вычисления площади, известной только в среде исполнения.
Что же может компилятор сделать для нас благодаря всем этим преимуществам? Если я запущу теперь все четыре фрагмента, то получу такие результаты:
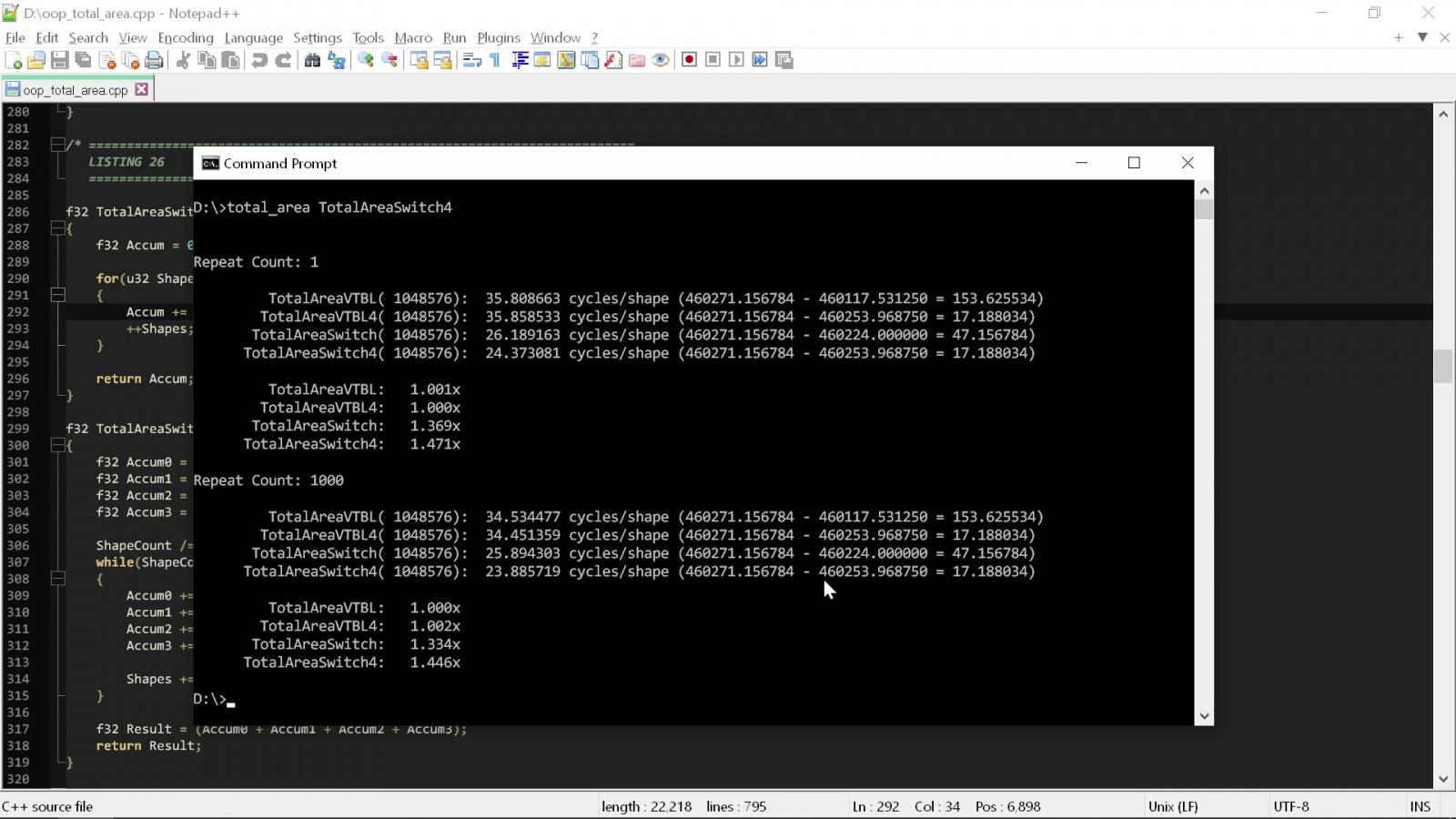
При изучении результатов мы можем заметить кое-что довольно примечательное: всего одно изменение — старомодный стиль кодинга вместо стиля «чистого» кода — дало нам мгновенное увеличение производительности в полтора раза. Это полуторакратное улучшение мы получаем без затрат, нам ничего не пришлось делать, кроме как удалить излишний код, необходимый для применения полиморфизма C++.
То есть нарушив первое правило чистого кода, являющееся одним из его основным столпов, мы способны снизить затраты с 35 до 24 тактов на фигуру, и это подразумевает, что следующий этому правилу код в полтора раза медленнее того, который ему не следует. Если сравнивать на уровне «железа», то требования к производительности снижаются с iPhone 14 Pro Max до iPhone 11 Pro Max. Три-четыре года эволюции оборудования уничтожены, потому что кто-то сказал использовать полиморфизм вместо операторов switch.
Но мы только начали.
Что, если мы нарушим и другие правила? Что, если мы нарушим второе правило — «запрет на знания о внутреннем устройстве»? Что, если наши функции могут использовать знание того, с чем они работают, чтобы повысить свою эффективность?
Если снова взглянуть на оператор switch получения площади, то можно заметить, что все вычисления площадей схожи:
case Shape_Square: {Result = Shape.Width*Shape.Width;} break;
case Shape_Rectangle: {Result = Shape.Width*Shape.Height;} break;
case Shape_Triangle: {Result = 0.5f*Shape.Width*Shape.Height;} break;
case Shape_Circle: {Result = Pi32*Shape.Width*Shape.Width;} break;Во всех них или ширина умножается на высоту, или ширина на ширину, иногда с коэффициентом наподобие пи, после чего они делятся пополам в случае треугольника или умножаются на пи в случае круга, и так далее.
Это одна из причин, по которым я считаю операторы switch очень удобными (в отличие от защитников «чистого» кода)! Они позволяют очень легко разглядеть паттерн. Если код упорядочен по операции, а не по типу, очень легко изучать его и выявлять общие паттерны. И наоборот: если вы взглянете на версию с классами, то, вероятно, никогда не заметите подобный паттерн, не только потому, что вам помешает большое количество бойлерплейта, но и потому, что защитники «чистого» кода рекомендуют помещать каждый класс в отдельный файл, ещё больше снижая вероятность того, что вы заметите что-то подобное.
Поэтому архитектурно я в общем случае не согласен с иерархиями классов, но дело не только в этом. Единственное, что я хочу сейчас подчеркнуть — мы можем сильно упростить оператор switch, заметив паттерн.
И помните: я не специально выбирал такой пример! Этот пример используют для наглядности сами защитники чистого кода. Поэтому я не выбрал намеренно пример, в котором можно выявить паттерн — просто очень вероятно, что вы сможете это сделать, потому что большинство вещей схожего типа имеют схожую алгоритмическую структуру, поэтому, как и ожидалось, это здесь произошло.
Чтобы использовать этот паттерн, мы можем создать простую таблицу, сообщающую нам, какой коэффициент нужно использовать для каждого типа. Если для типов с одним параметром, например, для круга и квадрата, мы дублируем ширину в высоту, то можно написать существенно более простую функцию для площади:
/* ========================================================================
LISTING 27
======================================================================== */
f32 const CTable[Shape_Count] = {1.0f, 1.0f, 0.5f, Pi32};
f32 GetAreaUnion(shape_union Shape)
{
f32 Result = CTable[Shape.Type]*Shape.Width*Shape.Height;
return Result;
}Два цикла суммирования в этой версии полностью одинаковы, их не нужно изменять, они просто вызывают GetAreaUnion вместо GetAreaSwitch, а в остальном идентичны.
Посмотрим, что произойдёт при запуске этой новой версии и сравнении с предыдущими циклами:
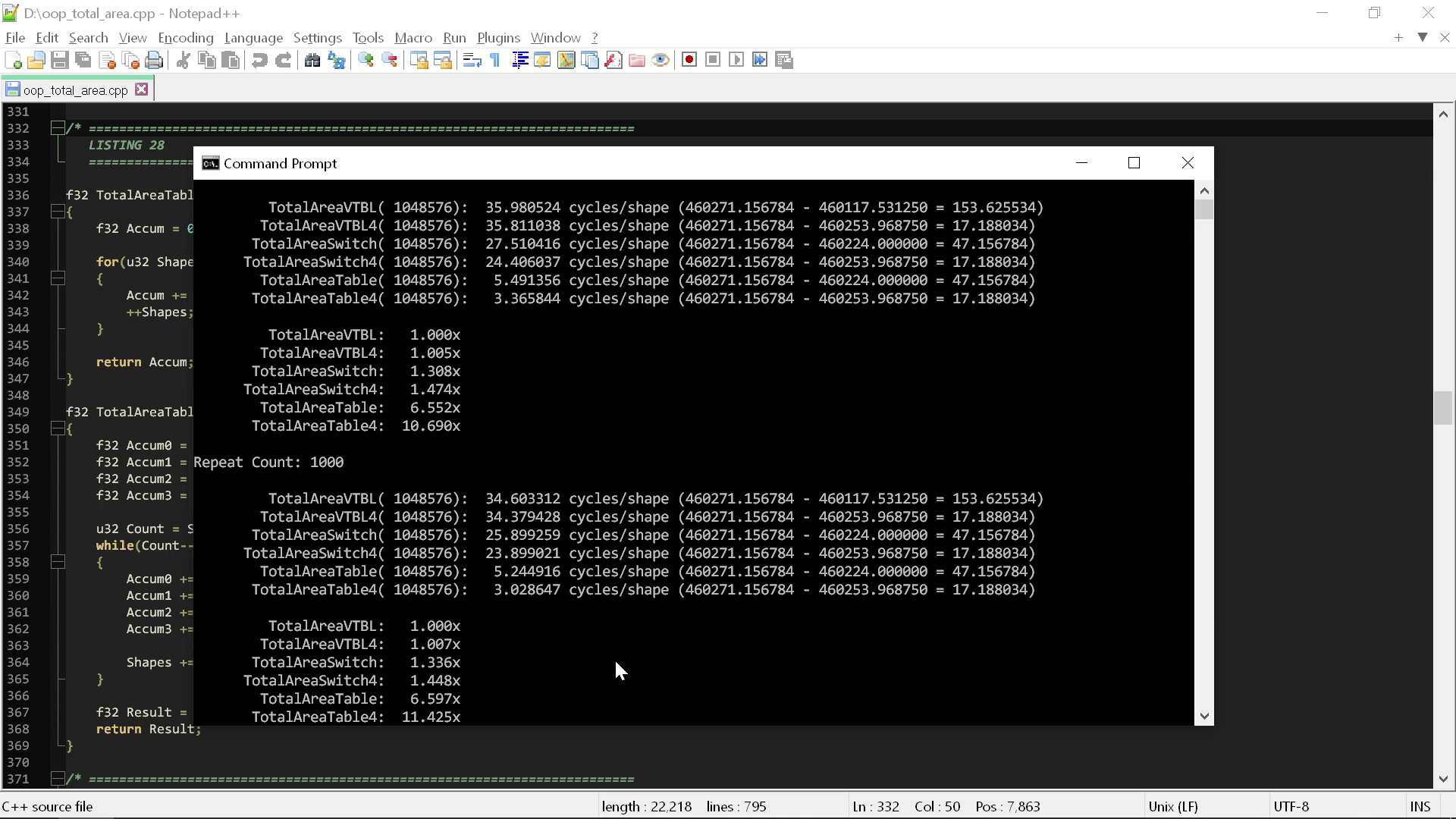
Здесь мы воспользовались тем, что знаем о самих типах, с которыми работаем, по сути, переключившись с на основе типов на
И чтобы добиться этого, нам не понадобилось ничего, кроме как одна операция поиска в таблице и одна строка кода! Это не только намного быстрее, но и гораздо проще семантически. Меньше токенов, меньше операций, меньше строк кода.
То есть вместо того, чтобы требовать обязательной неосведомлённости операции о внутреннем устройстве данных и связав модель данных с нужной нам операцией, мы снизили затраты до 3,0-3,5 тактов на серию фигур. Мы получили десятикратное повышение скорости по сравнению с «чистой» версией кода, следующей первым двум правилам.
Десятикратное повышение производительности настолько существенно, что его невозможно даже сравнить на аналогии с iPhone, потому что в бенчмарках iPhone такой разницы уже нет. Если мы опустимся до iPhone 6 (самого старого телефона, встречающегося в современных бенчмарках), то он всего в три раза медленнее iPhone 14 Pro Max. То есть чтобы описать разницу, мы даже не можем больше использовать телефоны.
Если взглянуть на производительность однопоточного десктопного компьютера, то десятикратное повышение скорости — это переход от среднего современного CPU mark до среднего CPU mark аж 2010 года! Первые два правила концепции «чистого кода» уничтожают 12 лет эволюции оборудования.
Но как бы это ни шокировало, мы протестировали это лишь на одной простой операции. Мы практически не пользовались правилами «функции должны быть маленькими» и «функции должны выполнять только одну операцию», потому что работаем с очень простой задачей. А что, если мы добавим ещё один аспект к нашей задаче, чтобы более можно было более непосредственно следовать этим правилам?
Ниже я написал точно такую же иерархию, что и раньше, но на этот раз добавил ещё одну виртуальную функцию, сообщающую, сколько углов у каждой из фигур:
/* ========================================================================
LISTING 32
======================================================================== */
class shape_base
{
public:
shape_base() {}
virtual f32 Area() = 0;
virtual u32 CornerCount() = 0;
};
class square : public shape_base
{
public:
square(f32 SideInit) : Side(SideInit) {}
virtual f32 Area() {return Side*Side;}
virtual u32 CornerCount() {return 4;}
private:
f32 Side;
};
class rectangle : public shape_base
{
public:
rectangle(f32 WidthInit, f32 HeightInit) : Width(WidthInit), Height(HeightInit) {}
virtual f32 Area() {return Width*Height;}
virtual u32 CornerCount() {return 4;}
private:
f32 Width, Height;
};
class triangle : public shape_base
{
public:
triangle(f32 BaseInit, f32 HeightInit) : Base(BaseInit), Height(HeightInit) {}
virtual f32 Area() {return 0.5f*Base*Height;}
virtual u32 CornerCount() {return 3;}
private:
f32 Base, Height;
};
class circle : public shape_base
{
public:
circle(f32 RadiusInit) : Radius(RadiusInit) {}
virtual f32 Area() {return Pi32*Radius*Radius;}
virtual u32 CornerCount() {return 0;}
private:
f32 Radius;
};У прямоугольника четыре угла, у треугольника — три, у круга их нет, и так далее. Я изменю определение задачи: вместо вычисления суммы площадей серии фигур мы будем вычислять сумму взвешенных по углам площадей, которую я определю как единицу, поделённую на единицу плюс количество углов.
Как и в случае с суммированием площадей, для этого нет никаких причин, я просто пытаюсь работать в рамках примера. Я добавил простейшее, что смог придумать, а затем добавил к этому очень простую математику.
Чтобы изменить «чистый» цикл суммирования, мы добавляем необходимую математику и дополнительный вызов виртуальной функции:
f32 CornerAreaVTBL(u32 ShapeCount, shape_base **Shapes)
{
f32 Accum = 0.0f;
for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex)
{
Accum += (1.0f / (1.0f + (f32)Shapes[ShapeIndex]->CornerCount())) * Shapes[ShapeIndex]->Area();
}
return Accum;
}
f32 CornerAreaVTBL4(u32 ShapeCount, shape_base **Shapes)
{
f32 Accum0 = 0.0f;
f32 Accum1 = 0.0f;
f32 Accum2 = 0.0f;
f32 Accum3 = 0.0f;
u32 Count = ShapeCount/4;
while(Count--)
{
Accum0 += (1.0f / (1.0f + (f32)Shapes[0]->CornerCount())) * Shapes[0]->Area();
Accum1 += (1.0f / (1.0f + (f32)Shapes[1]->CornerCount())) * Shapes[1]->Area();
Accum2 += (1.0f / (1.0f + (f32)Shapes[2]->CornerCount())) * Shapes[2]->Area();
Accum3 += (1.0f / (1.0f + (f32)Shapes[3]->CornerCount())) * Shapes[3]->Area();
Shapes += 4;
}
f32 Result = (Accum0 + Accum1 + Accum2 + Accum3);
return Result;
}Я мог бы сказать, что это нужно засунуть в ещё одну функцию, добавив ещё один слой косвенных действий. Но опять таки, чтобы не давать «чистому» коду кредит доверия, я оставлю это в явном виде.
Чтобы изменить версию с оператором switch, нужно, по сути, внести те же изменения. Сначала мы добавим ещё один оператор switch для количества углов с case, в точности отражающими версию с иерархией:
/* ========================================================================
LISTING 34
======================================================================== */
u32 GetCornerCountSwitch(shape_type Type)
{
u32 Result = 0;
switch(Type)
{
case Shape_Square: {Result = 4;} break;
case Shape_Rectangle: {Result = 4;} break;
case Shape_Triangle: {Result = 3;} break;
case Shape_Circle: {Result = 0;} break;
case Shape_Count: {} break;
}
return Result;
}Затем мы вычисляем точно так же, как в версии с иерархией:
/* ========================================================================
LISTING 35
======================================================================== */
f32 CornerAreaSwitch(u32 ShapeCount, shape_union *Shapes)
{
f32 Accum = 0.0f;
for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex)
{
Accum += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[ShapeIndex].Type))) * GetAreaSwitch(Shapes[ShapeIndex]);
}
return Accum;
}
f32 CornerAreaSwitch4(u32 ShapeCount, shape_union *Shapes)
{
f32 Accum0 = 0.0f;
f32 Accum1 = 0.0f;
f32 Accum2 = 0.0f;
f32 Accum3 = 0.0f;
ShapeCount /= 4;
while(ShapeCount--)
{
Accum0 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[0].Type))) * GetAreaSwitch(Shapes[0]);
Accum1 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[1].Type))) * GetAreaSwitch(Shapes[1]);
Accum2 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[2].Type))) * GetAreaSwitch(Shapes[2]);
Accum3 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[3].Type))) * GetAreaSwitch(Shapes[3]);
Shapes += 4;
}
f32 Result = (Accum0 + Accum1 + Accum2 + Accum3);
return Result;
}Как и в версии с общей суммой площадей, код в реализации с иерархией классов и реализации со switch выглядит почти идентично. Единственная разница заключается в вызове виртуальной функции или в выполнении оператора switch.
Перейдя к версии с таблицей, мы сможем увидеть, как здорово смешивать операции и данные! В отличие от предыдущих версий, единственное, что здесь нужно изменить — это значения в таблице! Нам необязательно получать вспомогательную информацию о фигуре — можно объединить количество углов и коэффициент площади непосредственно в таблицу, а код во всём остальном остаётся совершенно таким же:
/* ========================================================================
LISTING 36
======================================================================== */
f32 const CTable[Shape_Count] = {1.0f / (1.0f + 4.0f), 1.0f / (1.0f + 4.0f), 0.5f / (1.0f + 3.0f), Pi32};
f32 GetCornerAreaUnion(shape_union Shape)
{
f32 Result = CTable[Shape.Type]*Shape.Width*Shape.Height;
return Result;
}Если мы запустим эти функции «площадей с углами», то сможем понять, как на их производительность повлияло добавление второго свойства фигур:
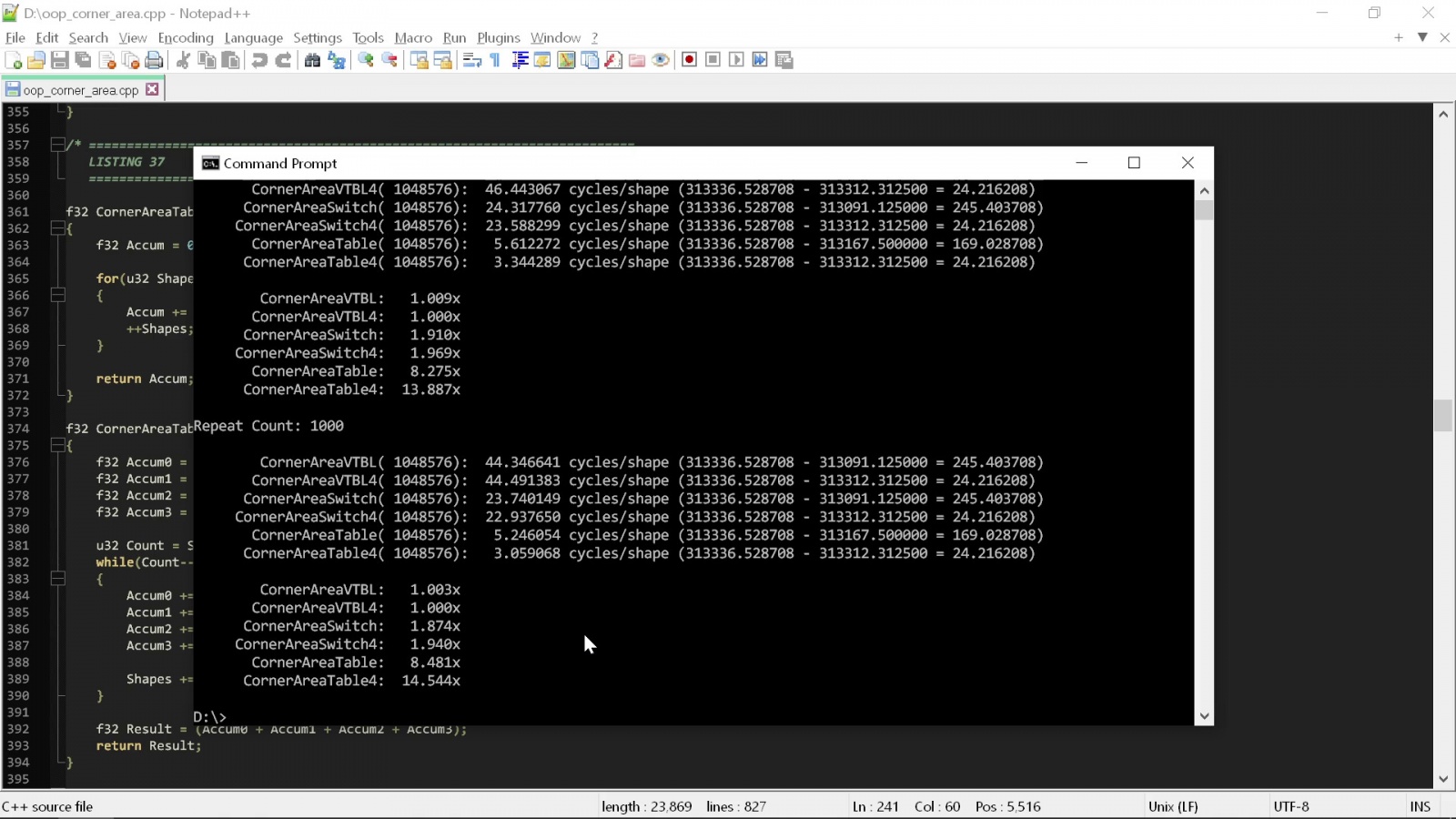
Как видите, эти результаты ещё хуже для «чистого» кода. Версия с оператором switch, которая раньше была всего лишь в полтора раза быстрее, теперь быстрее почти в два раза, а версия с таблицей поиска почти в пятнадцать раз быстрее.
Это демонстрирует ещё более глубокую «чистого» кода: чем больше усложняется задача, тем больше эти идеи вредят производительности. При попытке масштабировать «чистые» техники на реальные объекты со множеством свойств подобные вездесущие проблемы падения производительности будут встречаться в коде повсюду.
Чем больше вы используете методологию «чистого» кода, тем меньше компилятор способен понять, что вы делаете. Всё разделено на отдельные программные единицы, спрятано за вызовы виртуальных функций и так далее. Каким бы умным ни был компилятор, он практически ничего не может сделать с подобным кодом.
Хуже того, с таким кодом мало что можете сделать и вы! Как я показывал выше, простые действия наподобие извлечения значений из таблицы и устранение операторов switch реализовать просто, если архитектура вашей кодовой базы основана на её функциях. Если она основана на типах, это сделать гораздо сложнее, а может, даже невозможно без переписывания большого объёма кода.
Итак, мы перескочили с десятикратной разницы в скорости на пятнадцатикратную, просто добавив фигурам ещё одно свойство. Это аналогично возврату «железа» 2023 года в 2008 год! Вместо уничтожения 12 лет мы уничтожаем 14 лет, просто добавив один новый параметр в определение задачи.
Это ужасно само по себе. Но можно заметить, что я ещё не упомянул оптимизацию! Кроме того, чтобы гарантировать, что это не циклически порождаемая зависимость, ради тестирования я ничего не оптимизировал!
Теперь давайте посмотрим, что будет, если пропустить эти процедуру через слегка оптимизированную AVX-версию тех же вычислений:
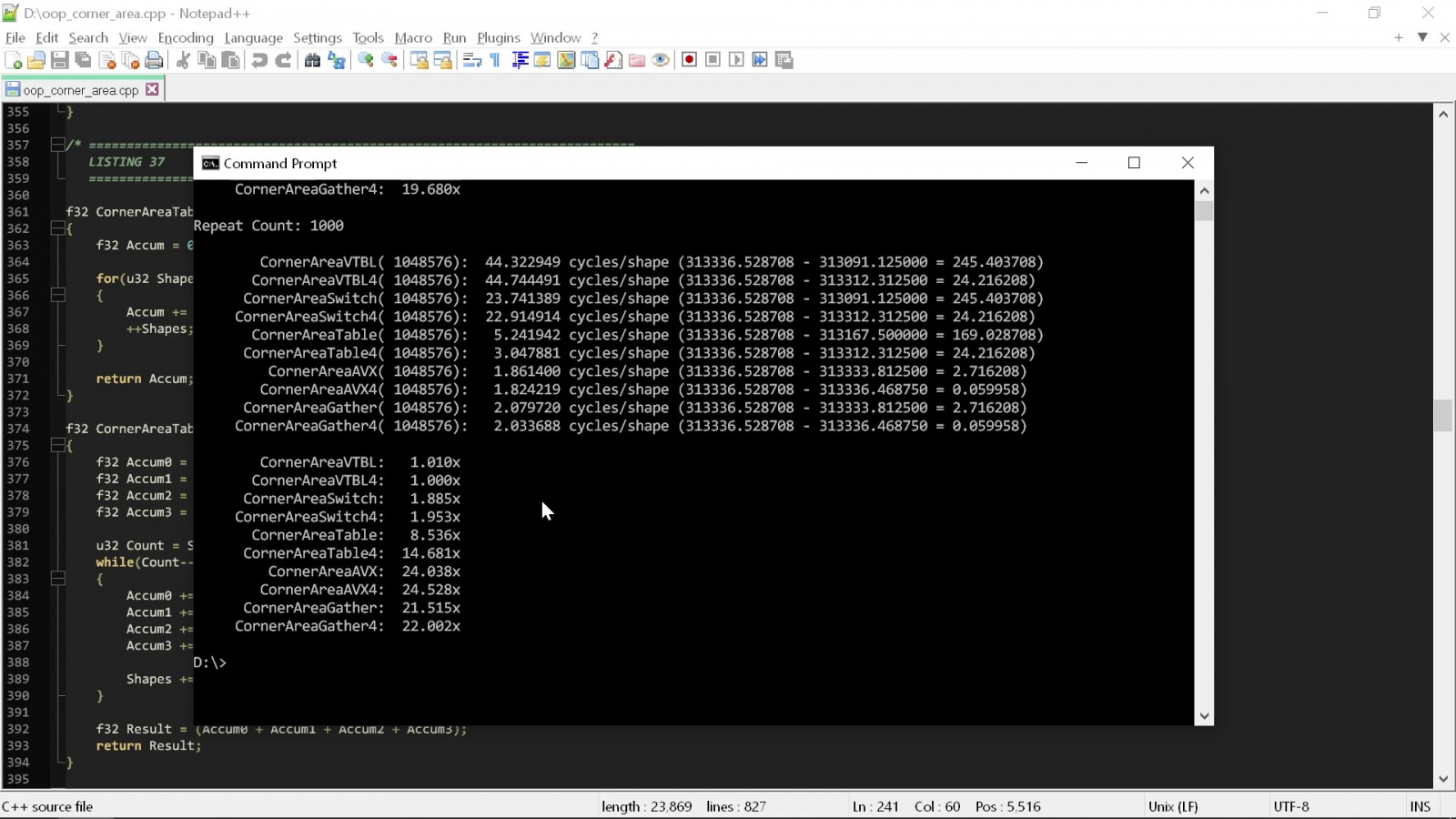
Разница в скорости составляет порядка 20-25 раз, и, разумеется, ни в какой части оптимизированного AVX кода не используется ничего даже отдалённо напоминающего принципы «чистого» кода.
То есть мы выбрасываем четыре правила. А как насчёт пятого?
Откровенно говоря, принцип «не повторяйся» вполне приемлем. Как видно из кода, мы не особо повторялись. Возможно, повторялись, если считать четыре развёрнутые версии сложения, но это нужно было лишь для демонстрации. На самом деле, если вы не проводите подобные измерения, то вам и не понадобятся обе такие процедуры.
Если «DRY» означает нечто более строгое, например, «не создавай две отдельные таблицы, в которых кодируются версии одинаковых коэффициентов», то иногда я не согласился бы с этим, потому что для достаточной производительности нам может понадобиться пойти на это. Но если в общем случае «DRY» просто означает «не пиши один и тот же код дважды», то это кажется разумным советом.
И самое важное то, что нам не нужно нарушать это правило, чтобы писать код с достаточной производительностью.
То есть я утверждаю, что из пяти принципов чистого кода, влияющих на структуру кода, учитывать нужно один, а четыре совершенно точно не нужно. Почему? Потому что, как вы могли заметить, ПО сегодня чрезвычайно медленное. Оно работает крайне плохо по сравнению с тем, как могло бы быстрое современное оборудование выполнять наше ПО.
Если вы спросите, почему программное обеспечение медленное, ответов может быть множество. И то, какой из них самый важный, зависит от конкретной среды разработки и методологии кодинга.
Но для большого сегмента компьютерной индустрии ответ на вопрос «почему ПО медленное» будет таким: «из-за „чистого“ кода». Почти все идеи, лежащие в основе методологии «чистого» кода, ужасно влияют на производительность, и их нельзя использовать.
Правила «чистого» кода были разработаны, потому что кто-то подумал, что они позволят создавать более удобные в поддержке кодовые базы. Даже если бы это так, вы должны задаться вопросом: «А какой ценой?»
Нельзя просто отказаться от десятка или больше лет эволюции производительности оборудования, только чтобы немного упростить жизнь программистов. Наша работа заключается в написании программ, хорошо работающих на оборудовании, которое у нас есть. Если из-за этих правил производительность ПО такая плохая, то они просто неприемлемы.
Мы всё равно можем попытаться выработать эмпирические правила, помогающие в упорядочивании, поддержке и читаемости кода. Это хорошие цели! Но подобные правила для этого не подходят. Их надо перестать повторять, или дополнять большой звёздочкой и сноской «и ваш код будет работать в пятнадцать или более раз хуже».
Автор:
JustJeremy





