Код, графики, попытка анализа — все под катом.
Решето Эратосфена на новый лад
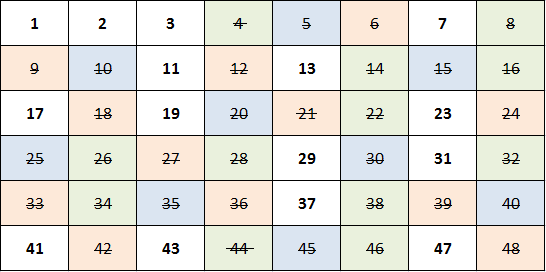
Нам нужно вычеркнуть из натурального ряда поочередно все числа, кратные 2-м, 3-м, 5-и и так далее? Нет ничего проще! Пустим вдоль оси x функцию «синус» с соответственно подправленным периодом, а сами синусы перемножим:
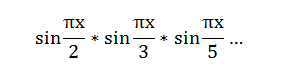
Функция совершенно естественным образом занулится на всех составных числах и обойдет простые. Для 3-х сомножителей таким образом мы найдем все простые вплоть до 47, а дальше останется только домножать на синус со следующим простым числом в аргументе
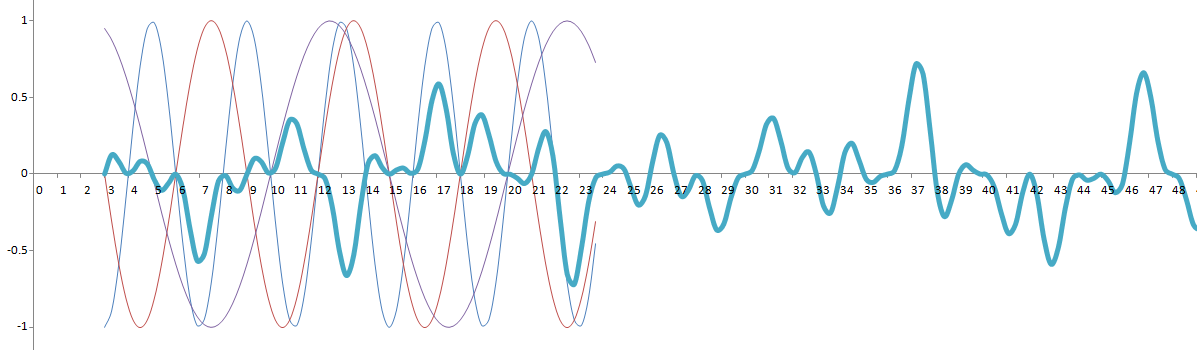
Тут, признаться, нас ждут проблемы. Хорошо анализировать функцию, когда она определена аналитически сразу на всей числовой оси. А не рекурсивно, как в нашем случае. Более того, даже попытка «сшить» ее в той точке x, где добавляется очередной сомножитель, приводит лишь к непрерывности функции в этой точке, но не гладкости. Похоже, так себе идея.
Что делает человек с университетским образованием, когда видит произведение синусов? (достает свой диплом, напивается и рыдает). Он пытается преобразовать произведение в сумму!
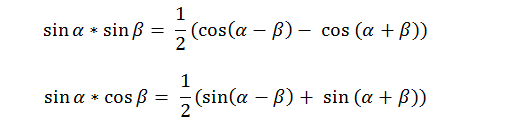
И тут нас ждет некий сюрприз
Пара первых произведений (мы опустили множитель ½ в степени n.)
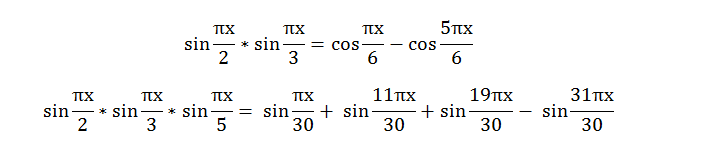
Вы заметили, да? Числители все сплошь простые числа! Вот почему, как говорят аналитики, так полезно смотреть на данные «глазками». Если копать дальше, то уже на следующем этапе среди числителей начнут попадаться и составные, но, так или иначе, процент простых будет очень велик.
Чтобы исследовать тему дальше, написал простую программу на C#
В первом варианте (тут не показан) я перемножал подряд синусы со всеми натуральными числами подряд – в конце концов, лишний ноль в произведении не помеха, как говорится). Это привело к интересному эффекту – в окончательной сумме синусов, когда мы уже избавились от всех произведений, появлялись подобные слагаемые, некоторые из которых при приведении уничтожали друг друга. Это сразу приводило к многообразию дальнейших вариантов – что делать с теми из них, которые взаимно сокращались, их числители тоже часто были простыми? Однако оказалось, что если брать в качестве новых множителей только простые числа, этот эффект уходит и подобных слагаемых не возникает (это эмпирический факт, без доказательства).
Интересно, что получаемые в этой итерационной последовательности числа (множители в числителе тригонометрических функций) растут с сумасшедшей скоростью. Уже для 15-й итерации (когда мы дошли всего лишь до простого числа 47 как множителя под синусом, на выходе – 16 384 слагаемых) максимальное число превысило 1 квинтиллион (название этой величины — единицы с 18-ю нулями — мне пришлось смотреть в Википедии), а максимальное простое приблизилось к нему. Это уже близко к пределу 64-битной величины long в C#, но причина остановки на 15 итерациях даже не в этом – проверка на простоту начинает занимать непотребно долгое время для следующего шага, во всяком случае, тем тупым лобовым способом, которым я это запрограммировал. Результат:
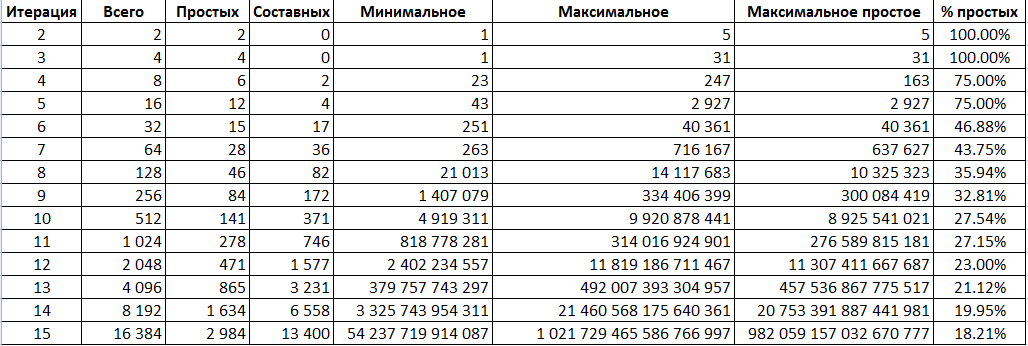
Интересный вопрос – можно ли каким-то образом избавиться от составных чисел, прореживая результат очередной итерации? Я не нашел никакой закономерности, у полученных составных числителей вполне могут быть простые «потомки» и наоборот, так что этот вопрос остался открытым. Первые 4 поколения выглядят вот так (составные – желтые):
![]()
Если взять потомков 3-й итерации, среди которых — 6 простых и 2 составных, то порожденные ими ветки до 15-го поколения включительно дают вот такие количества простых:
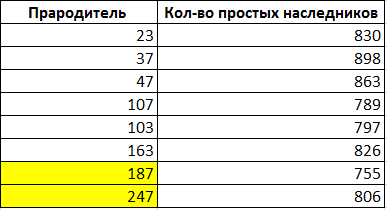
Никакой системы не прослеживается.
Ну и еще один подсчет. Известна формула для оценки количества простых чисел, попадающих в некий интервал натуральных. Предположим, что мы берем произвольную выборку чисел из интервала между MIN и MAX в каждой итерации, и сравним теоретическое количество простых с полученным нами:
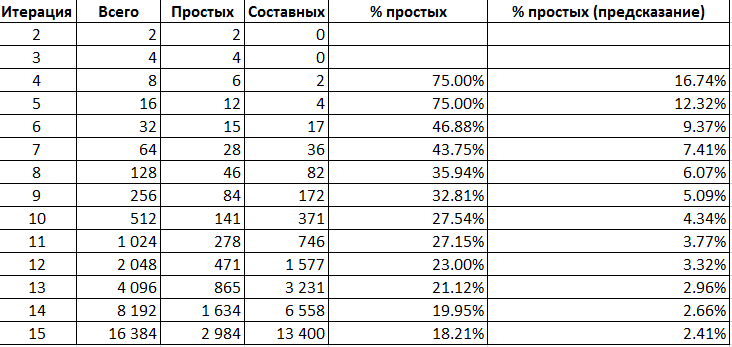
Предсказание получено по известной формуле MAX/LN(MAX) – MIN/LN(MIN). Как видим, в нашем процессе процент простых чисел заметно выше, хоть и падает.
Если вам не хватило всяких нумерологических загадок в этой статье, то вот еще одна. Сумма модулей числителей в ПРАВОЙ ЧАСТИ таблицы, то есть потомков второго слагаемого в разложении sin πx/2*sin πx/3, а именно cos 5πx/6, выглядит так:
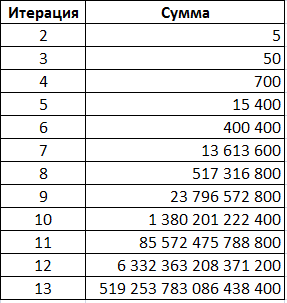
В левой части таблицы все суммы совершенно не круглые
Автор: Владимир Комен