В мире существует около 14 000 видов муравьёв, каждый из которых имеет собственное название. Но, даже если вы зададитесь такой целью, вы не найдёте ни в одном биологическом справочнике муравья Лэнгтона. Дело в том, что этот муравей — математическая абстракция, модель для описания поведения динамической системы. Иногда кажется, что математики вообще неравнодушны к муравьям — вспомним хотя бы уже ставший классическим муравьиный алгоритм. Да и во всяких логических моделях и задачах муравьи встречаются довольно часто.
От хаоса к строгому порядку
Познакомимся с муравьём Лэнгтона поближе. Он живёт на бесконечной плоскости, состоящей из белых клеток. У него есть два неиссякаемых ведёрка — одно с белой краской, другое с чёрной. Муравей перемещается по клеткам плоскости от одной клетки к другой. При этом он выполняет несложный алгоритм:
-
Если клетка белая, то муравей перекрашивает её в чёрный цвет, поворачивает на 90° направо (по часовой стрелке) и делает шаг вперёд.
-
Если клетка чёрная, то муравей перекрашивает её в белый цвет, поворачивает на 90° налево (против часовой стрелки) и делает шаг вперёд.
Вот, собственно, и всё. Невесёлая жизнь у муравья Лэнгтона, но, как мы увидим, он не готов мириться с такой возмутительной ситуацией и всеми силами старается сбежать.
Написать программу, которая моделирует поведение муравья Лэнгтона, — это несложная задача. В сети есть много примеров реализации этого алгоритма: попроще и посложнее — с набором дополнительных настроек.
Попробуйте понаблюдать за перемещениями этого муравья по его клетчатой плоскости. На первый взгляд, его шаги полностью хаотичны — никакого порядка не наблюдается. Но, перефразируя известную поговорку, если долго наблюдать за муравьём, можно увидеть, как он убегает. Где-то после 10 000 шагов муравей вдруг осознаёт тщетность бытия и предпринимает попытку сбежать — он начинает строить периодическую конструкцию, каждые 104 шага перемещают его на две клетки по диагонали. После этого шаги повторяются. Поведение муравья уже никогда не станет хаотичным — теперь он так и будет двигаться по широкой диагональной полосе-магистрали, состоящей из чёрных и белых клеток.
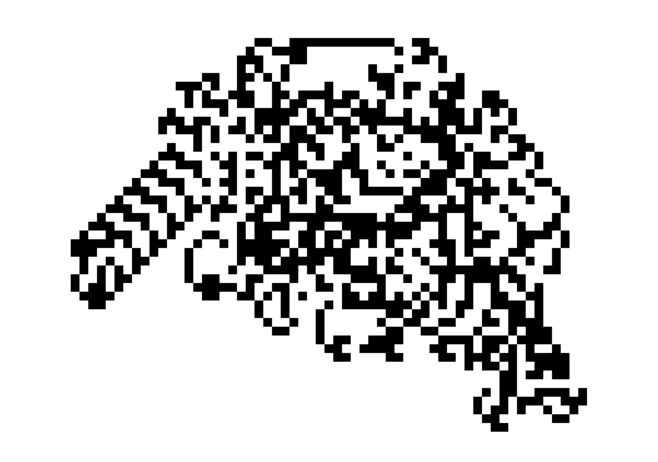
Уже само это внезапное изменение поведения муравья Лэнгтона заставляет задуматься — как из полностью хаотичной системы вдруг рождается строгий порядок?! Но у нашего муравья есть ещё более впечатляющее свойство. Что будет, если до начала движения муравья раскрасить конечное количество некоторых из близлежащих к стартовой точке клеток в чёрный цвет? Изменится от этого поведение муравья?
В книге Иэна Стюарта «Величайшие математические задачи» приведено захватывающее описание этого эксперимента: «Мы можем выбрать для этого любые клетки: это может быть случайный набор, чёрный квадрат или Мона Лиза. Их может быть миллион, или миллиард, или ещё больше, но не бесконечное количество».
Что же в итоге произойдёт? Во всех поставленных экспериментах муравей, поблуждав по клеткам, рано или поздно снова начинал строить свою магистраль при помощи всё тех же 104 шагов. Складывается впечатление, что в муравье заложен сложный самообучающийся алгоритм, который в итоге приводит его к регулярной повторяющейся структуре шагов. На самом же деле алгоритм всё тот же — два правила, описанные в начале статьи. Но самое занимательное во всей этой модели то, что математики до сих пор не знают ответа на следующие вопросы:
-
Всегда ли муравей переходит к упорядоченному движению?
-
Если ответ на предыдущий вопрос положительный, то является ли магистраль из повторяющихся 104 шагов единственной конструкцией («аттрактором»), которую в итоге начинает строить муравей?
Единственное, что математики могут сказать с уверенностью, — это то, что независимо от начальной конфигурации клеток свободолюбивый муравей не останется навечно в замкнутой области. Американский учёный Кристофер Лэнгтон придумал своего муравья ещё в 1984 году. С тех пор так никто и не смог объяснить странное поведение этой загадочной модели.
Модификации муравья Лэнгтона
Муравей Лэнгтона — это по сути клеточный автомат, регулярная решётка, в которой на каждом шаге цвет ячеек меняется по определённому набору правил, обычно в зависимости от цвета соседних ячеек. Самый известный клеточный автомат — это игра «Жизнь» английского математика Джона Конвея. Учёные придумали множество разнообразных клеточных автоматов, но, пожалуй, ни один из них не сравнится по загадочности с нашим муравьём.
Кстати, как и другие клеточные автоматы, муравей Лэнгтона имеет свои модификации. Например, иногда нашего муравья нагружают ведёрками с дополнительными красками. В этом случае для каждого цвета задаются отдельные правила поворота. Ещё можно подсадить к муравью других муравьёв (каждого с ведёрком своего цвета) и посмотреть, как они будут взаимодействовать. Есть также варианты с гексагональной решёткой, на которой используется шесть различных вариантов поворота: без изменений, 180°, 60° направо, 60° налево, 120° направо и 120° налево.

Также можно менять алгоритм поведения каждого муравья в системе. Для этого придумали способ кодирования алгоритма в виде строки из символов R — повернуть направо и L — повернуть налево. В этой записи каждая позиция соответствует цвету клетки, на которую пришёл муравей. Для классического муравья Лэнгтона запись будет такая: RL. Также иногда добавляют ещё две команды: C — продолжить движение в том же направлении (иногда используется буква F), U — развернуться на 180° (иногда используется буква B). Муравьи с изменёнными алгоритмами поведения начинают вести себя совсем по-другому — уже не всегда строят магистрали. Многие из них сразу начинают составлять симметричные узоры. Так себя ведут, например, муравьи с повторяющимися парами: LL и RR. Например, LLRR.

Вы можете воспользоваться одной из готовых программ или сами запрограммировать эту замечательную и загадочную систему и поэкспериментировать с различными вариантами её реализации. Для муравьёв можно придумывать новые алгоритмы, менять их количество, начальное направление движения и стартовые точки на плоскости. Можно также провести опыты с начальной раскраской некоторых клеток на плоскости. Например, свободолюбивый муравей с правилом RL умеет с успехом выбираться из замкнутого квадрата.

Для этого клеточного автомата можно придумать множество модификаций с разным поведением, но классический муравей Лэнгтона, с которым мы познакомились, пока так и остаётся одной из нерешённых задач математики. Меня всегда поражали подобные системы с простейшими формулировками и необъяснимым поведением. Они напоминают нам о том, как много мы ещё не знаем о математических законах устройства нашего мира. Возможно, решение таких задач в будущем приведёт нас к пониманию чего-то большего, чем поведение простейшего клеточного автомата.
Статья была впервые опубликована на другом ресурсе 29 марта 2021.
Автор: Александр Клименков






