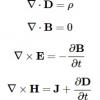В Serokell мы занимаемся не только коммерческими проектами, но стараемся изменить мир к лучшему. Например, работаем над улучшением главного инструмента всех хаскелистов – Glasgow Haskell Compiler (GHC). Мы сосредоточились на расширении системы типов под впечатлением от работы Ричарда Айзенберга "Зависимые типы в Haskell: теория и практика".
В нашем блоге Владислав уже рассказывал о том, почему в Haskell не хватает зависимых типов и как мы планируем их добавить. Мы решили перевести этот пост на русский, чтобы как можно больше разработчиков могло использовать зависимые типы и сделать дальнейший вклад в развитие Haskell как языка.
Текущее положение дел
Зависимые типы – это то, чего мне больше всего не хватает в Haskell. Давайте обсудим почему. От кода мы хотим:
- производительности, то есть скорости выполнения и низкого потребления памяти;
- поддерживаемости и простоты в понимании;
- корректности, гарантированной способом его составления.
С имеющимся технологиями редко удается добиться всех трех характеристик, но с поддержкой зависимых типов Haskell задача упрощается.
Стандартный Haskell: эргономика + производительность
В основе Haskell лежит простая система: полиморфное лямбда-исчисление с ленивыми вычислениями, алгебраическими типами данных и классами типов. Именно это сочетание особенностей языка позволяет нам писать элегантный, поддерживаемый и в то же время производительный код. Чтобы обосновать это утверждение, вкратце сравним Haskell с более популярными языками.
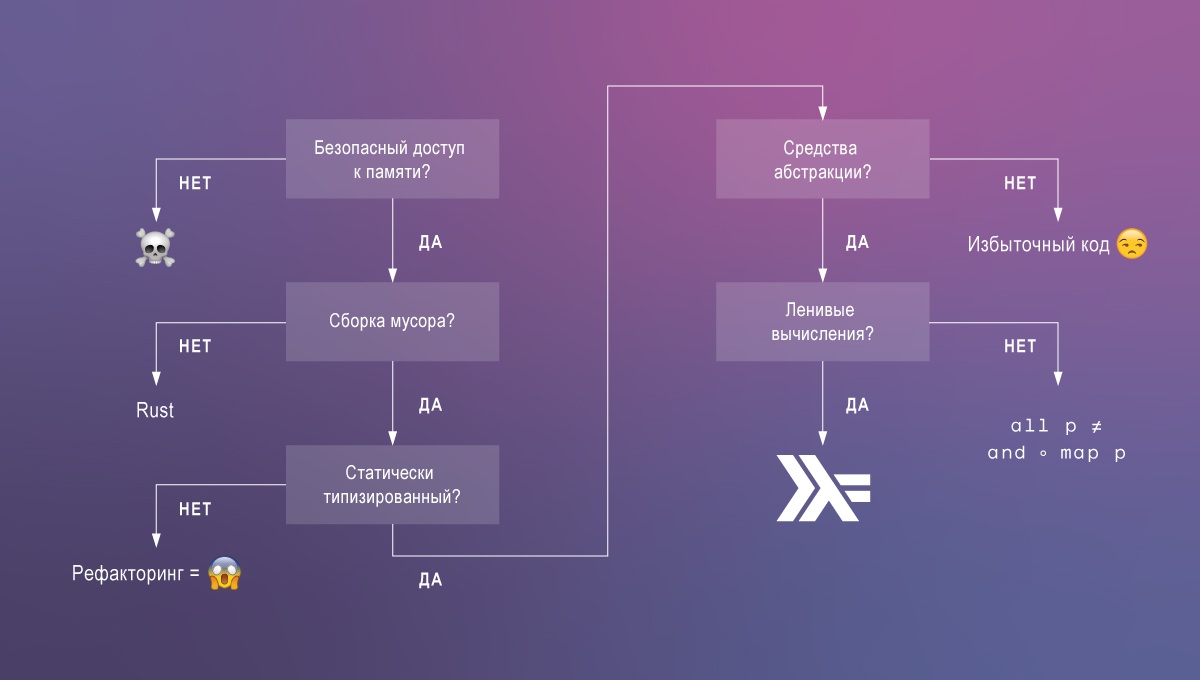
Языки с небезопасным доступом к памяти, такие как C, приводят к самым серьезным ошибкам и уязвимостям (например, переполнение буфера, утечки памяти). Иногда такие языки нужны, но чаще всего их применение – идея так себе.
Языки с безопасным доступом к памяти образуют две группы: те, что полагаются на сборщик мусора, и Rust. По всей видимости, Rust уникален в том, что предлагает безопасный доступ к памяти без сборщика мусора. Также есть уже не поддерживаемый Cyclone и другие исследовательские языки в этой группе. Но в отличие от них, Rust находится на пути к популярности. Недостаток в том, что несмотря на безопасность, управление памятью в Rust нетривиально и выполняется вручную. В приложениях, которые могут позволить себе применение сборщика мусора, время разработчиков лучше потратить на решение других задач.
Остаются языки со сборщиками мусора, которые мы далее разобьем на две категории, основываясь на их системе типов.
Динамически типизированные (или, скорее, монотипизированные) языки, такие как JavaScript или Clojure, не предоставляют статический анализ, а следовательно не могут обеспечить тот же уровень уверенности в правильности кода (и нет, тесты не могут заменить типы – нужно и то, и другое!).
Статически типизированные языки, такие как Java или Go, часто имеют сильно ограниченную систему типов. Это вынуждает программистов писать избыточный код и пускать в дело небезопасные возможности языка. Например, отсутствие обобщенных типов в Go вынуждает использовать interface{} и приведение типов времени выполнения. Также нет разделения между вычислениями с побочными эффектами (ввод, вывод) и чистыми вычислениями.
Наконец, среди языков с безопасным доступом к памяти, сборщиком мусора и мощной системой типов, Haskell выделяется ленивостью. Ленивые вычисления крайне полезны для написания композируемого, модульного кода. Они позволяют разложить на вспомогательные определения любые части выражений, в том числе конструкции, задающие поток управления.
Haskell кажется почти идеальным языком, пока вы не осознаете насколько он далек от полного раскрытия своего потенциала с точки зрения статической проверки по сравнению со средствами доказательства теорем, такими как Agda.
В качестве простого примера того, где система типов Haskell недостаточно мощна, рассмотрим оператор индексирования списка из Prelude (или индексирование массива из пакета primitive):
(!!) :: [a] -> Int -> a
indexArray :: Array a -> Int -> aНичто в этих сигнатурах типов не отражает требования, что индекс должен быть неотрицательным и меньше длины коллекции. Для программного обеспечения с высокими требованиями к надежности это недопустимо.
Agda: эргономика + корректность
Средства доказательства теорем (например, Coq) — программные инструменты, которые позволяют с помощью компьютера разрабатывать формальные доказательства математических теорем. Для математика использование таких средств похоже на написание доказательств на бумаге. Различие в беспрецедентной строгости, требуемой компьютером, чтобы установить правильность такого доказательства.
Для программиста, однако, средство доказательства теорем не так уж отличается от компилятора для эзотерического языка программирования с невероятной системой типов (и, возможно, интегрированной средой разработки), и посредственным (или даже отсутствующим) всем остальным. Средство доказательства теорем – это, по сути, языки программирования, авторы которых все время потратили на разработку системы типизации и забыли, что программы еще надо запускать.
Заветная мечта разработчиков верифицированного программного обеспечения – это средство доказательства теорем, которое было бы хорошим языком программирования с высококачественными генератором кода и средой выполнения. В данном направлении экспериментировали в том числе создатели Idris. Но это язык со строгими (энергичными) вычислениями, а его реализация на данный момент не отличается стабильностью.
Среди всех средств доказательства теорем больше всего по душе хаскелистам Agda. Во многом она похожа на Haskell, но с более мощной системой типов. Мы в Serokell применяем её, чтобы доказывать различные свойства наших программ. Мой коллега Даня Рогозин написал серию статей об этом.
Вот тип функции lookup аналогичной оператору (!!) из Haskell:
lookup : ∀ (xs : List A) → Fin (length xs) → AПервый параметр здесь имеет тип List A, который соответствует [a] в Haskell. Однако мы даем ему имя xs, чтобы обращаться к нему в оставшейся части сигнатуры типа. В Haskell мы можем обращаться к аргументам функции только в теле функции на уровне термов:
(!!) :: [a] -> Int -> a -- can't refer to xs here
(!!) = xs i -> ... -- can refer to xs hereА вот в Agda мы можем ссылаться на это значение xs и на уровне типов, что мы и делаем во втором параметре lookup, Fin (length xs). Функция, ссылающаяся на свой параметр на уровне типов, называется зависимой функцией и является примером зависимых типов.
Второй параметр в lookup имеет тип Fin n для n ~ length xs. Значение типа Fin n соответствует числу в диапазоне [0, n), так что Fin (length xs) это неотрицательное число меньше длины входного списка. Именно это нам и нужно, чтобы представить валидный индекс элемента списка. Грубо говоря, lookup ["x","y","z"] 2 проверку типов пройдет, а lookup ["x","y","z"] 42 не пройдет.
Когда дело доходит до запуска программ на Agda, мы можем скомпилировать их в Haskell с помощью бэкенда MAlonzo. Но производительность генерируемого кода будет неудовлетворительна. Это не вина MAlonzo: ему приходится вставлять многочисленные unsafeCoerce, чтобы GHC принимал код, уже проверенный Agda. Но тот же unsafeCoerce снижает производительность (по итогам обсуждения этой статьи выяснилось, что проблемы с производительностью возможно вызваны иными причинами – прим. автора).
Это ставит нас в затруднительное положение: нам приходится использовать Agda для моделирования формальной проверки, а затем заново реализовывать ту же функциональность на Haskell. При такой организации рабочих процессов наш код на Agda выступает в качестве спецификации, проверяемой компьютером. Это лучше спецификации на естественном языке, но далеко от идеала. Цель – если код скомпилировался, то он будет работать в соответствии со спецификацией.
Haskell с расширениями: корректность + производительность

Стремясь к статическим гарантиям языков с зависимыми типами, GHC прошел долгий путь. В него добавляли расширения, увеличивающие выразительность системы типов. Я начал использовать Haskell, когда GHC 7.4 был новейшей версией компилятора. Уже тогда у него были основные расширения для продвинутого программирования на уровне типов: RankNTypes, GADTs, TypeFamilies, DataKinds, и PolyKinds.
И все же полноценных зависимых типов в Haskell нет до сих пор: ни зависимых функций (Π-типов), ни зависимых пар (Σ-типов). С другой стороны, хотя бы кодировка для них у нас есть!
Нынешние практики таковы:
- кодировать функции на уровне типов в виде закрытых семейств типов,
- использовать дефункционализацию, чтобы сделать возможным ненасыщенное применение функций,
- устранять разрыв между термами и типами с помощью единичных типов.
Это приводит к значительному количеству избыточного кода, но библиотека singletons автоматизирует его генерацию посредством Template Haskell.
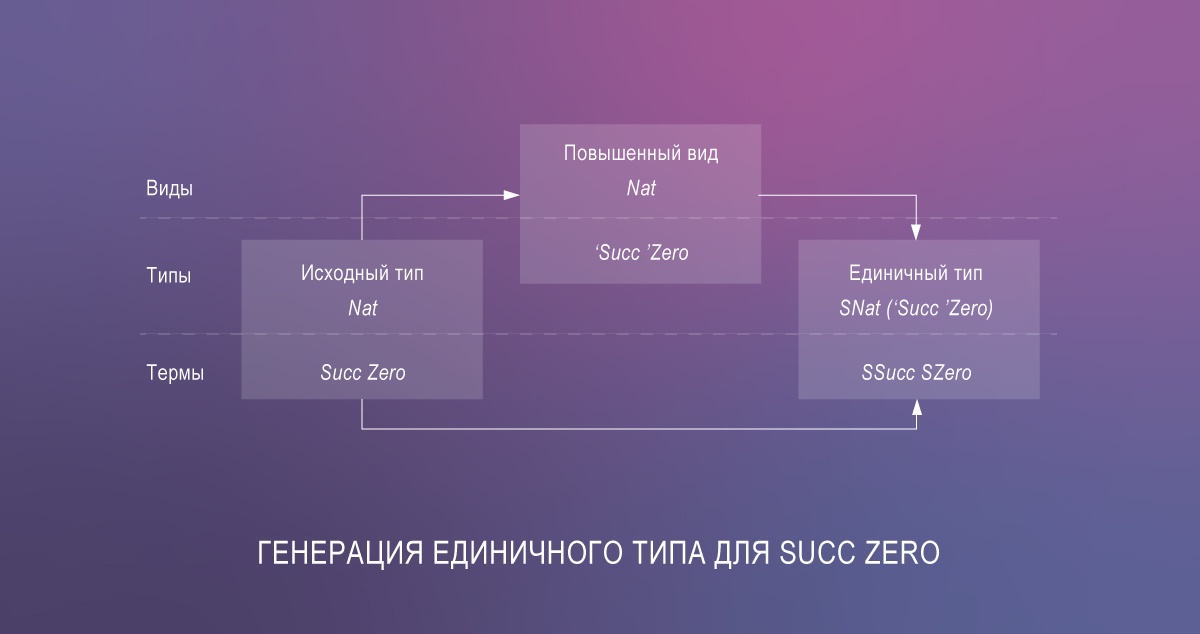
Так что самые смелые и решительные могут закодировать зависимые типы в Haskell уже сейчас. В качестве демонстрации вот реализация функции lookup аналогичная варианту на Agda:
{-# OPTIONS -Wall -Wno-unticked-promoted-constructors -Wno-missing-signatures #-}
{-# LANGUAGE LambdaCase, DataKinds, PolyKinds, TypeFamilies, GADTs,
ScopedTypeVariables, EmptyCase, UndecidableInstances,
TypeSynonymInstances, FlexibleInstances, TypeApplications,
TemplateHaskell #-}
module ListLookup where
import Data.Singletons.TH
import Data.Singletons.Prelude
singletons
[d|
data N = Z | S N
len :: [a] -> N
len [] = Z
len (_:xs) = S (len xs)
|]
data Fin n where
FZ :: Fin (S n)
FS :: Fin n -> Fin (S n)
lookupS :: SingKind a => SList (xs :: [a]) -> Fin (Len xs) -> Demote a
lookupS SNil = case{}
lookupS (SCons x xs) =
case
FZ -> fromSing x
FS i' -> lookupS xs i'И вот сессия GHCi, показывающая, что lookupS действительно отклоняет слишком большие индексы:
GHCi, version 8.6.2: http://www.haskell.org/ghc/ :? for help
[1 of 1] Compiling ListLookup ( ListLookup.hs, interpreted )
Ok, one module loaded.
*ListLookup> :set -XTypeApplications -XDataKinds
*ListLookup> lookupS (sing @["x", "y", "z"]) FZ
"x"
*ListLookup> lookupS (sing @["x", "y", "z"]) (FS FZ)
"y"
*ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS FZ))
"z"
*ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ)))
<interactive>:5:34: error:
• Couldn't match type ''S n0' with ''Z'
Expected type: Fin (Len '["x", "y", "z"])
Actual type: Fin ('S ('S ('S ('S n0))))
• In the second argument of 'lookupS', namely '(FS (FS (FS FZ)))'
In the expression:
lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ)))
In an equation for 'it':
it = lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ)))Этот пример показывает, что осуществимое не означает практичное. Я рад, что в Haskell есть языковые возможности для реализации lookupS, но в то же время меня беспокоит возникающая при этом ненужная сложность. Вне исследовательских проектов такой стиль кода я бы не посоветовал.
В этом конкретном случае, мы могли бы достичь такого же результата при меньшей сложности, используя индексированные длиной векторы. Однако прямой перевод кода с Agda лучше раскрывает проблемы, с которыми приходится иметь в других обстоятельствах.
Вот некоторые из них:
- Отношение типизации
a :: tи отношение назначения видаt :: kразличны.5 :: Integerверно в термах, но не в типах."hi" :: Symbolверно в типах, но не в термах. Это приводит к необходимости семейства типовDemoteдля сопоставления видов и типов. - Стандартная библиотека использует
Intв качестве представления списковых индексов (иsingletonsиспользуетNatв повышенных определениях).IntиNat– неиндуктивные типы. Несмотря на большую эффективность по сравнению с унарным кодированием натуральных чисел, они не очень хорошо работают с индуктивными определениями, такими какFinилиlookupS. Из-за этого мы переопределяемlengthкакlen. - В Haskell нет встроенных механизмов повышения функций на уровень типов.
singletonsкодирует их в виде закрытых семейств типов и применяет дефункционализацию, чтобы обойти отсутствие частичного применения семейств типов. Эта кодировка сложна. Вдобавок, нам пришлось поместить определениеlenв цитату Template Haskell, чтобыsingletonsсгенерировал её аналог на уровне типов,Len. - Нет встроенных зависимых функций. Приходится использовать единичные типы, чтобы преодолеть разрыв между термами и типами. Вместо обычного списка мы передаем
SListна входlookupS. Поэтому мы должны держать в голове сразу несколько определений списков. Также это приводит к накладным расходам во время исполнения программы. Они возникают из-за конвертации между обычными значениями и значениями единичных типов (toSing,fromSing) и из-за передачи процедуры конвертации (ограничениеSingKind).
Неудобство – это меньшая из проблем. Хуже то, что эти возможности языка работают ненадежно. Например, я сообщил о проблеме #12564 еще в 2016 году, а еще есть #12088 того же года. Обе проблемы препятствуют реализации программ более продвинутых, чем примеры из учебников (вроде индексирования списков). Эти баги GHC до сих пор не исправлены, и причина, как мне кажется, в том, что у разработчиков просто не хватает времени. Количество людей, активно работающих над GHC, удивительно мало, поэтому до некоторых вещей не доходят руки.
Резюме
Ранее я упомянул, что от кода мы хотим всех трех свойств, так что вот таблица, иллюстрирующая текущее положение дел:
| Стандартный Haskell | Agda | Haskell с расширениями | |
|---|---|---|---|
| Эргономика и поддерживаемость | + | + | - |
| Производительность | + | - | + |
| Корректность, гарантированная способом составления | - | + | + |
Светлое будущее
Из трех доступных вариантов каждый имеет свои недостатки. Тем не менее, мы можем их исправить:
- Взять стандартный Haskell и добавить зависимые типы напрямую вместо неудобного кодирования через
singletons. (Легче сказать, чем сделать). - Взять Agda и реализовать эффективный генератор кода и RTS для неё. (Легче сказать, чем сделать).
- Взять Haskell с расширениями, исправить баги и продолжить добавлять новые расширения, чтобы упростить кодирование зависимых типов. (Легче сказать, чем сделать).
Хорошая новость в том, что все три варианта сходятся в одной точке (в каком-то смысле). Представьте себе самое минимальное расширение стандартного Haskell, которое добавляет зависимые типы, и следовательно, позволяет гарантировать корректность кода способом его составления. Код на Agda можно компилировать (транспилировать) в этот язык без unsafeCoerce. А Haskell с расширениями – это, в некотором смысле, незаконченный прототип этого языка. Что-то понадобится улучшить, а что-то убрать, но в конечном итоге, мы достигнем желаемого результата.
Избавление от singletons
Хорошим показателем прогресса можно считать упрощение библиотеки singletons. По мере реализации зависимых типов в Haskell, обходные пути и специальная обработка частных случаев, реализованные в singletons, становятся не нужны. В конечном итоге нужда в этом пакете пропадет полностью. Например, в 2016 году с помощью расширения -XTypeInType я убрал KProxy из SingKind и SomeSing. Это изменение стало возможным благодаря объединению типов и видов. Сравните старые и новые определения:
class (kparam ~ 'KProxy) => SingKind (kparam :: KProxy k) where
type DemoteRep kparam :: *
fromSing :: SingKind (a :: k) -> DemoteRep kparam
toSing :: DemoteRep kparam -> SomeSing kparam
type Demote (a :: k) = DemoteRep ('KProxy :: KProxy k)
data SomeSing (kproxy :: KProxy k) where
SomeSing :: Sing (a :: k) -> SomeSing ('KProxy :: KProxy k)В старых определениях k встречается исключительно в позициях вида, справа от аннотаций вида t :: k. Мы используем kparam :: KProxy k для переноса k в типы.
class SingKind k where
type DemoteRep k :: *
fromSing :: SingKind (a :: k) -> DemoteRep k
toSing :: DemoteRep k -> SomeSing k
type Demote (a :: k) = DemoteRep k
data SomeSing k where
SomeSing :: Sing (a :: k) -> SomeSing kВ новых определениях k свободно перемещается между позициями вида и типа, так что нам больше не нужен KProxy. Причина в том, что начиная с GHC 8.0 типы и виды относятся к одной и той же синтаксической категории.
В стандартном Haskell есть три полностью разделенных мира: термы, типы и виды. Если посмотреть на исходный код GHC 7.10, то можно увидеть обособленный синтаксический анализатор для видов и обособленную проверку. В GHC 8.0 их больше нет: синтаксический анализатор и проверка для типов и видов общие.
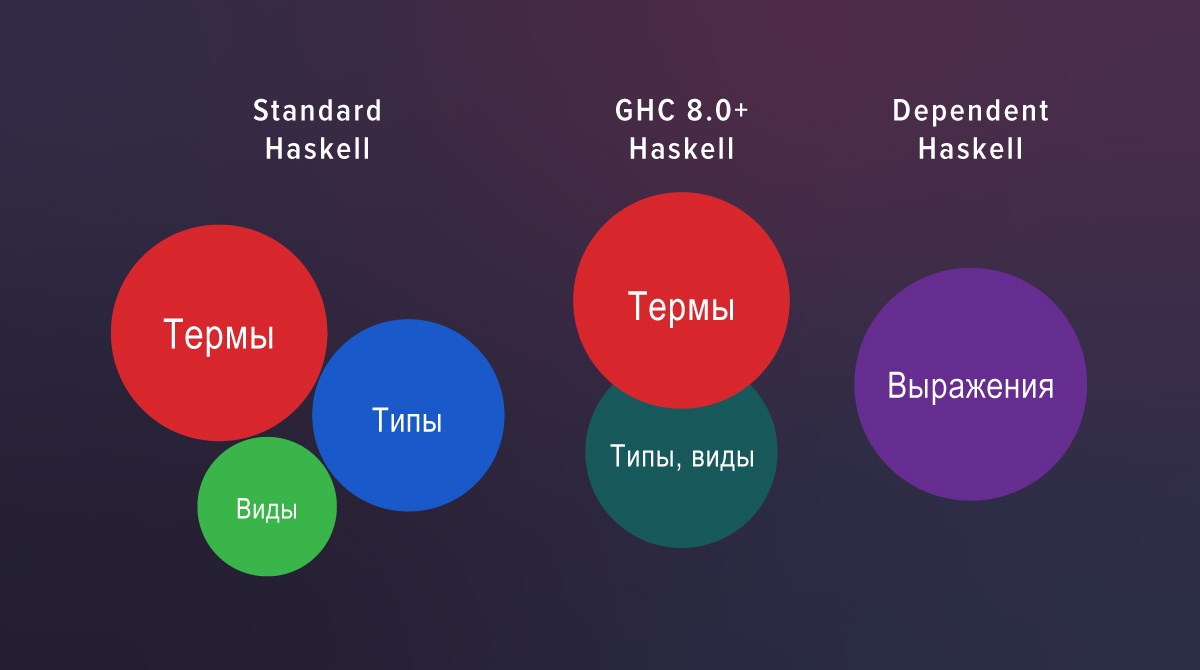
В Haskell с расширениями вид – это всего лишь роль, в которой выступает тип:
f :: T z -> ... -- 'z' это тип
g :: T (a :: z) -> ... -- 'z' это вид
h :: T z -> T (a :: z) -> ... -- 'z' это и тип, и видВ GHC 8.0–8.4 все еще оставались некоторые различия между разрешением имен в типах и видах. Но к GHC 8.6 я их свел к минимуму: создал расширение StarIsType и внес функциональность TypeInType в PolyKinds. Оставшиеся различия я сделал предупреждением к GHC 8.8, и полностью устранил в GHC 8.10 (перевод данного параграфа обновлен, в оригинале проделанные работы описываются как будущие задачи – прим. автора).
Каков следующий шаг? Давайте взглянем на SingKind в последней версии singletons:
class SingKind k where
type Demote k = (r :: Type) | r -> k
fromSing :: Sing (a :: k) -> Demote k
toSing :: Demote k -> SomeSing kСемейство типов Demote необходимо для учета расхождений между отношением типизации a :: t и отношением назначения вида t :: k. Чаще всего (для алгебраических типов данных), Demote это тождественное отображение:
type Demote Bool = Booltype Demote [a] = [Demote a]type Demote (Either a b) = Either (Demote a) (Demote b)
Следовательно, Demote (Either [Bool] Bool) = Either [Bool] Bool. Это наблюдение побуждает нас сделать следующее упрощение:
class SingKind k where
fromSing :: Sing (a :: k) -> k
toSing :: k -> SomeSing kDemote не понадобился! И, в самом деле, это сработало бы как в случае Either [Bool] Bool, так и с другими алгебраическими типами данных. На практике, однако, мы имеем дело и с неалгебраическими типами данных: Integer, Natural, Char, Text, и так далее. Если их использовать в качестве видов, они не населены: 1 :: Natural верно на уровне термов, но не на уровне типов. Из-за этого мы имеем дело с такими определениями:
type Demote Nat = Natural
type Demote Symbol = TextРешение этой проблемы в повышении примитивных типов. Например, Text определен так:
-- | A space efficient, packed, unboxed Unicode text type.
data Text = Text
{-# UNPACK #-} !Array -- payload (Word16 elements)
{-# UNPACK #-} !Int -- offset (units of Word16, not Char)
{-# UNPACK #-} !Int -- length (units of Word16, not Char)
data Array = Array ByteArray#
data Int = I# Int#Если мы как положено повысим ByteArray# и Int# на уровень типов, то сможем использовать Text вместо Symbol. Сделав то же самое с Natural и, возможно, парой других типов, можно избавиться от Demote, так ведь?
Увы, не так. В вышесказанном я закрыл глаза на самый главный тип данных: функции. У них тоже особый инстанс Demote:
type Demote (k1 ~> k2) = Demote k1 -> Demote k2
type a ~> b = TyFun a b -> Type
data TyFun :: Type -> Type -> Type~> это тип, с помощью которого в singletons кодируются функции на уровне типов, основываясь на закрытых семействах типов и дефункционализации.
Сперва может показаться неплохой идеей объединить ~> и ->, так как оба означают тип (вид) функции. Проблема в том, что -> в позиции типа и -> в позиции вида означают разные вещи. На уровне термов, все функции из a в b имеют тип a -> b. На уровне типов же, только конструкторы из a в b имеют тип a -> b, но не синонимы типов и не семейства типов. В целях вывода типов, GHC предполагает, что из f a ~ g b следует f ~ g и a ~ b, что верно для конструкторов, но не для функций – оттого и ограничение.
Следовательно, чтобы повышать функции на уровень типов, но сохранить вывод типов, нам придется вынести конструкторы в отдельный тип. Назовем его a :-> b, для него действительно будет верно, что из f a ~ g b следует f ~ g и a ~ b. Остальные функции по-прежнему будут иметь тип a -> b. Например, Just :: a :-> Maybe a, но при этом isJust :: Maybe a -> Bool.
Когда с Demote будет покончено, последний шаг – избавиться от самого Sing. Для этого нам понадобится новый квантор, гибрид между forall и ->. Давайте посмотрим на функцию isJust повнимательнее:
isJust :: forall a. Maybe a -> Bool
isJust =
x ->
case x of
Nothing -> False
Just _ -> TrueФункция isJust параметризована типом a, а затем значением x :: Maybe a. Эти два параметра обладают различными свойствами:
- Явность. В вызове
isJust (Just "hello")мы передаемx = Just "hello"явно, аa = Stringвыводится компилятором неявно. В современном Haskell мы также можем форсировать явную передачу обоих параметров:isJust @String (Just "hello"). - Релевантность. Значение, передаваемое на вход в
isJustв коде, будет передаваться и во время исполнения программы: мы выполняем сопоставление с образцом посредствомcase, чтобы проверить, этоNothingилиJust. Потому значение считается релевантным. А вот его тип стирается и не подлежит сопоставлению с образцом: функция одинаково обрабатываетMaybe Int,Maybe String,Maybe Boolи т.д. Следовательно, он считается нерелевантным. Это свойство также называют параметричностью. - Зависимость. В
forall a. t, типtможет упоминатьa, и, следовательно, зависеть от конкретного переданногоa. Например,isJust @Stringимеет типMaybe String -> Bool, аisJust @Intимеет типMaybe Int -> Bool. Это значит, чтоforall– зависимый квантор. Заметьте разницу с параметром-значением: не важно, вызовем ли мыisJust NothingилиisJust (Just …), тип результата всегдаBool. Следовательно,->– это не зависимый квантор.
Чтобы выместить Sing, нам нужен квантор явный и релевантный, подобно a -> b, и в то же время зависимый, подобно forall (a :: k). t. Обозначим его как foreach (a :: k) -> t. Чтобы выместить SingI, также введем неявный релевантный зависимый квантор, foreach (a :: k). t. В результате singletons будут не нужны, так как мы только что добавили зависимые функции в язык.
Краткий взгляд на Haskell с зависимыми типами
С повышением функций на уровень типов и квантором foreach, мы сможем переписать lookupS следующим образом:
data N = Z | S N
len :: [a] -> N
len [] = Z
len (_:xs) = S (len xs)
data Fin n where
FZ :: Fin (S n)
FS :: Fin n -> Fin (S n)
lookupS :: foreach (xs :: [a]) -> Fin (len xs) -> a
lookupS [] = case{}
lookupS (x:xs) =
case
FZ -> x
FS i' -> lookupS xs i'Короче код не стал, все-таки singletons довольно неплохо прячет избыточный код. Однако новый код намного проще: больше нет Demote, SingKind, SList, SNil, SCons, fromSing. Нет использования TemplateHaskell, так как теперь мы можем вызывать функцию len напрямую вместо создания семейства типов Len. Производительность тоже будет лучше, так как больше не нужно преобразование fromSing.
Нам все еще приходится переопределять length как len, чтобы возвращать индуктивно определенный N вместо Int. Пожалуй, эту проблему лучше не рассматривать в рамках добавления зависимых типов в Haskell, ведь Agda тоже использует индуктивно определенный N в функции lookup.
В некоторых аспектах Haskell с зависимыми типами даже проще, чем стандартный Haskell. Все-таки в нем термы, типы и виды объединены в общий однородный язык. Я легко могу представить себе написание кода в таком стиле в коммерческом проекте, чтобы формально доказать правильность ключевых компонентов приложений. Многие библиотеки на Haskell смогут предоставить более безопасные интерфейсы без сложности, сопряженной с применением singletons.
Добиться этого будет не просто. Перед нами много инженерных проблем, затрагивающих все компоненты GHC: синтаксический анализатор, разрешение имен, проверку типов, и даже язык Core. Все понадобится модифицировать, или даже полностью перепроектировать.
Тезаурус
| Термин | Перевод | Пояснение |
| correct by construction | Код, корректность которого гарантирована способом его составления | Методология разработки, согласно которой корректность кода гарантируется способом его составления (например, применением системы типов), а не тестированием. |
| memory unsafe | С небезопасным доступом к памяти | Возможность в языке программирования вручную выделять и освобождать память, выполнять арифметику с указателями. |
| unityped | Монотипизированный | Термин, который ввел Bob Harper для более точного описания языков, традиционно называемых динамически типизированными. В таких языках проверки меток типов отложены до времени выполнения программы. |
| boilerplate | Избыточный код | Однотипный код с похожими или повторяющимися элементами, который невозможно обобщить из-за недостаточной выразительности языка. |
| generics | Обобщенные типы | Возможность системы типов обобщить типы введением параметра. Например, вместо введение конкретных типов «СписокЧисел» и «СписокСтрок», можно ввести обобщенный тип Список, применяя его как Список<Число> и Список<Строка>. |
| runtime cast | Приведение типов времени выполнения | Преобразование значения одного типа в значение другого типа с проверкой во время выполнения программы. |
| effectful computation | Вычисление с побочными эффектами | Вычисление, выполнение которого приводит к наблюдаемым эффектам помимо возврата вычисленного значения. |
| composable | Композируемый | Характеристика кода, отмечающая простоту его применения в другом коде посредством операций композиции. |
| control structures | Конструкции, задающие поток управления | Конструкции языка, применение которых влияет на порядок вычисления подвыражений. |
| proof assistant | Средство доказательства теорем | Программное обеспечение для формального доказательства математических гипотез. |
| strict (eager) evaluation | Строгие (энергичные) вычисления | Стратегия вычисления выражений, согласно которой значения аргументов функции вычисляются до вызова функции. |
| backend | Бэкенд | Компонент компилятора, транслирующий внутреннее представление программы в код на целевом языке. |
| singleton type | Единичный тип | Тип, населенный одним значением, определяемым инстанцированием соответствующего параметра на уровне типов. |
| promoted definitions | Повышенные определения | Определения закрытых семейств типов, которые соответствуют тем или иным функциям на уровне термов. |
Автор: Arseniy Seroka