Многие программисты думают, что Quick Sort — самый быстрый алгоритм из всех существующих. Отчасти это так. Но работает она действительно хорошо только если правильно выбран опорный элемент (тогда сложность составляет O (n log n)). В противном же случае асимптотика будет примерно такой же как и в пузырика (то-есть O (n2)).
Многие программисты думают, что Quick Sort — самый быстрый алгоритм из всех существующих. Отчасти это так. Но работает она действительно хорошо только если правильно выбран опорный элемент (тогда сложность составляет O (n log n)). В противном же случае асимптотика будет примерно такой же как и в пузырика (то-есть O (n2)).
При этом, если массив уже отсортирован, то алгоритм всё-равно будет работать не быстрее, чем за O (n log n)
Исходя из этого, я решил написать свой алгоритм для сортировки массива, который работал бы лучше за quick_sort. И если массив уже отсортирован, то не прогонять его кучу раз, как это бывает у многих алгоритмов.
«Дело было вечером, делать было нечего», — Сергей Михалков.
Требования:
- Лучший случай O (n)
- Средний случай O (n log n)
- Худший случай O (n log n)
- В среднем быстрее быстрой сортировки
А теперь давайте обо всём по порядку
Чтобы наш алгоритм всегда работал быстро, нужно чтобы в среднем случае асимптотика была хотя бы O (n log n), а в лучшем — O (n). Все мы прекрасно знаем, что в лучшем случае сортировка вставками работает за один проход. Но в худшем ей придётся гонять по массиву столько раз, сколько в нём элементов.
Предварительная информация
int* glue(int* a, int lenA, int* b, int lenB) {
int lenC = lenA + lenB;
int* c = new int[lenC]; // результирующий массив
int indx_a = 0;
int indx_b = 0;
int i = 0;
for (; i < lenC; ++i) {
if (indx_a < lenA) {
if (indx_b < lenB) { // Оба массива содержат элементы
c[i] = (a[indx_a] < b[indx_b]) ?
a[indx_a++] :
b[indx_b++];
continue;
} // Элементы есть только в первом
while (indx_a < lenA)
c[i++] = a[indx_a++];
}
else // Элементы есть только во втором
while (indx_b < lenB)
c[i++] = b[indx_b++];
break;
}
return c;
}
void glueDelete(int*& arr, int*& a, int lenA, int*& b, int lenB) {
if (lenA == 0) { // если первый пустой
delete[] a; // высвобождаем от него память
arr = b; // результирующий будет вторым массивом
return;
}
if (lenB == 0) { // если второй пустой
delete[] b; // высвобождаем от него память
arr = a; // результирующий будет вторым массивом
return;
}
int *copy = glue(a, lenA, b, lenB); // сливаем
delete[]a; // удаляемо ненужные массивы
delete[]b; // удаляемо ненужные массивы
arr = copy; // изменяем указатель
}
void insertionSort(int*& arr, int lo, int hi) {
for (int i = lo + 1; i <= hi; ++i)
for (int j = i; j > 0 && arr[j - 1] > arr[j]; --j)
swap(arr[j - 1], arr[j]);
}
Начальная версия алгоритма (не оптимальная):
Основная идея алгоритма состоит в так называемом поиске максимума (и минимума). На каждой итерации выбираем из массива элемент. Если он больше предыдущего максимума, то добавляем этот элемент в конец выборки. Иначе если он меньше предыдущего минимума, то дописываем этот элемент в начало. Иначе кладём в отдельный массив.
На вход функция принимает массив и количество элементов в этом массиве
void FirstNewGeneratingSort(int*& arr, int len)
Для хранения выборки из массива (наши максимумы и минимумы) и остальных элементов выделим память
int* selection = new int[len << 1]; // то же что и new int[len * 2]
int left = len - 1; // индекс для хранения новых минимальных элементов
int right = len; // индекс для хранения новых максимальных элементов
int* restElements = new int[len]; // для элементов, которые не входят в выборку
int restLen = 0; // индекс следующего элемента для добавления
Как видим, для хранения выборки мы выделили в 2 раза больше памяти, чем наш исходный массив. Это сделано на случай если у нас массив отсортирован и каждый следующий элемент будет новым максимумом. Тогда будет занята только вторая часть массива выборки. Или же наоборот (если отсортирован по убыванию).
Для выборки сначала нужны начальные минимум и максимум. Просто выберем первый и второй элементы
if (arr[0] > arr[1])
swap(arr[0], arr[1]);
selection[left--] = arr[0];
selection[right++] = arr[1];
Собственно сама выборка
for (int i = 2; i < len; ++i) {
if (selection[right - 1] <= arr[i]) // проверяем на новый максимум
{
selection[right++] = arr[i];
continue;
}
if (selection[left + 1] >= arr[i]) // проверяем на новый минимум
{
selection[left--] = arr[i];
continue;
}
restElements[restLen++] = arr[i]; // если элемент не попал в выборку, он попадёт сюда
}
Теперь у нас есть отсортированный набор элементов, и «остальные» элементы, которые нам ещё нужно отсортировать. Но сначала нужно произвести некоторые манипуляции с памятью.
Освобождаем неиспользуемую память
int selectionLen = right - left - 1; // длина выборки
int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); // в данном контексте просто копирует выборку
delete[] selection; // мы выделяли 2 * len памяти, и большая её часть скорее всего просто не используется, поэтому освобождаем лишнюю память
selection = copy; // изменяем указатель, так что теперь selection содержит только значащую информацию
delete[] arr; // далее будет рекурсивный вызов, а все элементы для сортировки у нас уже есть, поэтому освободим память от исходного массива
Делаем рекурсивный вызов сортировки для остальных элементов и сливаем их с выборкой
FirstNewGeneratingSort(restElements, restLen);
glueDelete(arr, selection, selectionLen, restElements, restLen);
void FirstNewGeneratingSort(int*& arr, int len) {
if (len < 2)
return;
int* selection = new int[len << 1];
int left = len - 1;
int right = len;
int* restElements = new int[len];
int restLen = 0;
if (arr[0] > arr[1])
swap(arr[0], arr[1]);
selection[left--] = arr[0];
selection[right++] = arr[1];
for (int i = 2; i < len; ++i) {
if (selection[right - 1] <= arr[i]) // проверяем на новый максимум
{
selection[right++] = arr[i];
continue;
}
if (selection[left + 1] >= arr[i]) // проверяем на новый минимум
{
selection[left--] = arr[i];
continue;
}
restElements[restLen++] = arr[i]; // если элемент не попал в выборку, он попадёт сюда
}
int selectionLen = right - left - 1; // длина выборки
int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); // в данном контексте просто копирует выборку
delete[] selection; // мы выделяли 2 * len памяти, и большая её часть в большинстве случаев просто не используется, поэтому освобождаем лишнюю память
selection = copy; // изменяем указатель, так что теперь selection содержит только значащую информацию
delete[] arr; // далее будет рекурсивный вызов, а все элементы для сортировки у нас уже есть, поэтому освободим память от исходного массива
FirstNewGeneratingSort(restElements, restLen);
glueDelete(arr, selection, selectionLen, restElements, restLen);
}
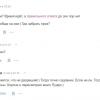
Проверим скорость работы алгоритма по сравнению с Quick Sort
Как видим, это совсем не то, чего мы хотели. Почти в 6 раз дольше, чем QuickSort! Но разы в этом контексте неуместно использовать, так как здесь значение имеет именно асимптотика. В данной реализации алгоритма в худшем случае первый и второй элементы будут минимальным и максимальным. И остальные будут скопированы в отдельный массив.
Сложность алгоритма:
- Худший случай: O (n 2)
- Средний случай: O (n 2)
- Лучший случай: O (n)
Хм, это ничем не лучше той же самой сортировки вставками. Да, действительно мы можем найти максимальный (минимальный) элемент очень быстро, и остальные просто не попадут в выборку.
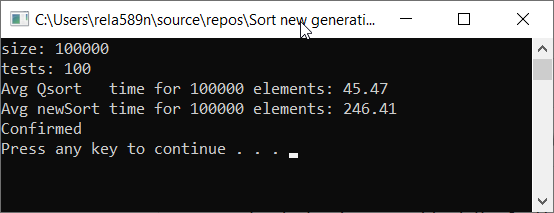
Можем попытаться оптимизировать сортировку слиянием. Для начала проверим скорость обычной сортировки слиянием:
void newGenerationMergeSort(int* a, int lo, int hi, int& minPortion) {
if (hi <= lo)
return;
int mid = lo + (hi - lo) / 2;
if (hi - lo <= minPortion) { // если количество элементов вмещается в минимальный блок, то выполняем нашу сортировку
int* part = glue(a + lo, hi - lo + 1, nullptr, 0); // просто копирует массив
FirstNewGeneratingSort(part, hi - lo + 1);
for (int i = lo; i <= hi; ++i) {
a[i] = part[i - lo];
}
delete[] part;
return;
}
newGenerationMergeSort(a, lo, mid, minPortion);
newGenerationMergeSort(a, mid + 1, hi, minPortion);
int* b = glue(a + lo, mid - lo + 1, a + mid + 1, hi - mid);
for (int i = lo; i <= hi; i++)
a[i] = b[i - lo];
delete[] b;
}
Для простоты использования нужна какая-нибудь обёртка
void newMergeSort(int *arr, int length) {
int portion = log2(length); // минимальный блок для нашей сортировки
portion *= portion;
newGenerationMergeSort(arr, 0, length - 1, portion);
}
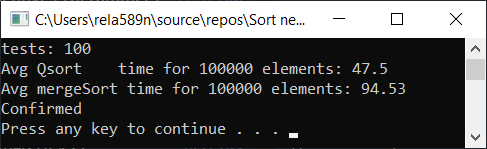
Результат тестирования:
Да, прирост в скорости наблюдается, но всё-же эта функция работает не так быстро, как Quick Sort. Тем более мы не можем говорить про O (n) на отсортированных массивах. Поэтому этот вариант тоже откидаем.
Варианты оптимизации первого варианта
-
Для того, чтобы сложность не была O (n2), мы можем складывать элементы, которые не попали в выборку не в 1 массив как ранее, а раскинуть на 2 массива. После чего останется просто отсортировать этих две подчасти, и слить их с нашей выборкой. В результате мы получим сложность равную O (n log n)
-
Как мы уже заметили, абсолютно максимальный (минимальный) элемент в сортируемом массиве может найтись довольно быстро, и это не очень эффективно. Вот тут в помощь нам вступает сортировка вставками. На каждой итерации выборки будем проверять, можем ли мы вставить поточный элемент в набор из последних, например, восьми вставленных.
Если сейчас не понятно, то не расстраивайтесь. Так и должно быть. Сейчас на коде всё станет ясно и вопросы пропадут.
Остаточный правильный вариант алгоритма:
Сигнатура такая же как и в предыдущем варианте
void newGenerationSort(int*& arr, int len)Но следует заметить, что данный вариант предполагает первым параметром указатель, на котором можно вызвать операцию delete[] (почему — мы увидим далее). То-есть когда мы выделяли память, мы именно для этого указателя присваивали адрес начала массива.
Предварительная подготовка
В данном примере так называемый «коэффициент навёрстывания» (catch up coefficient) — это просто константа со значением 8. Она показывает сколько максимум элементов мы попытаемся пройти, чтобы вставить новый «недо-максимум» или «недо-минимум» на своё место.
int localCatchUp = min(catchUp, len); // потому что мы не можем пытаться вставлять элемент за границами массива
insertionSort(arr, 0, localCatchUp - 1); // для начала сортируем первые localCatchUp элементов
if (len <= localCatchUp) // на случай если это массив на n <= catchUp элементов, а также
return; // это база рекурсии (так как при таких раскладах массив отсортирован)
Для хранения выборки создаём массив
Если что-то непонятно, то смотрите объяснение в начальной версии
int* selection = new int[len << 1]; // то же что и new int[len * 2]
int left = len - 1; // индекс для хранения новых минимальных элементов
int right = len; // индекс для хранения новых максимальных элементов
Заполним первые несколько элементов массива выборки
selection[left--] = arr[0];
for (int i = 1; i < localCatchUp; ++i) {
selection[right++] = arr[i];
}
Напомню, что в левую сторону от центра массива выборки идут новые минимумы, а в правую — новые максимумы
Создадим массивы для хранения не избранных элементов
int restLen = len >> 1; // то же что и len / 2
int* restFirst = new int[restLen];
int* restSecond = new int[restLen];
int restFirstLen = 0;
int restSecondLen = 0;
Теперь, самое главное — правильная выборка элементов из исходного массива
Цикл начинается с localCatchUp (потому что предыдущие элементы уже попали в нашу выборку как значения от которых мы будем отталкиваться). И проходит до конца. Так что после в конце концов все элементы распределятся либо в массив выборки либо в один из массивов недо-выборки.
Для проверки, можем ли мы вставить элемент в выборку, мы просто будем проверять больше (или равен) ли он элементу на 8 позиций левее (right − localCatchUp). Если это так, то мы просто одним проходом по этим элементам вставляем его на нужную позицию. Это было для правой стороны, то-есть для максимальных элементов. Таким же образом делаем с обратной стороны для минимальных. Если не удалось вставить его ни в одну сторону выборки значит кидаем его в один из rest-массивов.
Цикл будет выглядеть примерно так:
for (int i = localCatchUp; i < len; ++i) {
if (selection[right - localCatchUp] <= arr[i])
{
selection[right] = arr[i];
for (int j = right; selection[j - 1] > selection[j]; --j)
swap(selection[j - 1], selection[j]);
++right;
continue;
}
if (selection[left + localCatchUp] >= arr[i])
{
selection[left] = arr[i];
for (int j = left; selection[j] >= selection[j + 1]; ++j)
swap(selection[j], selection[j + 1]);
--left;
continue;
}
if (i & 1) { // i - непарное
restFirst[restFirstLen++] = arr[i];
}
else {
restSecond[restSecondLen++] = arr[i];
}
}
Опять же, что здесь происходит? Сначала пытаемся пихнуть элемент в максимумы. Не получается? — Если возможно, кидаем его в минимумы. При невозможности и это сделать — кладём его в restFirst или restSecond.
Самое сложное уже позади. Теперь после цикла у нас есть отсортированный массив с выборкой (элементы начинаются с индекса [left + 1] и оканчиваются в [right − 1]), а также массивы restFirst и restSecond длиной restFirstLen и restSecondLen соответственно.
Как и в предыдущем примере, перед рекурсивным вызовом высвобождаем память от основного массива (все его элементы мы уже и так сохранили)
delete[] arr; У нас массив selection может содержать много ячеек неиспользуемой памяти. Перед рекурсивным вызовом нужно освободить её.
Освобождаем неиспользуемую память
int selectionLen = right - left - 1; // просто длина нашей выборки
int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); // копируем все элементы выборки в новый массив
delete[] selection; // удаляем массив размером 2 * len элементов и
selection = copy; // вместо него используем ровно столько памяти, сколько нужно
Теперь запускаем нашу функцию сортировки рекурсивно для массивов restFirst и restSecond
Для понимания того как оно всё отработает, сначала нужно посмотреть код до конца. Пока что нужно просто поверить что после рекурсивных вызовов массивы restFirst и restSecond будут отсортированными.
newGenerationSort(restFirst, restFirstLen);
newGenerationSort(restSecond, restSecondLen);
И, наконец, нам нужно слить 3 массива в результирующий и назначить его указателю arr.
Можно было бы сначала слить restFirst + restSecond в какой-нибудь массив restFull, а потом уже производить слияние selection + restFull. Но данный алгоритм обладает таким свойством, что скорее всего массив selection будет содержать намного меньше элементов, чем любой из rest-массивов. Припустим в selection содержится 100 элементов, в restFirst — 990, а в restSecond — 1010. Тогда для создания restFull массива нужно произвести 990 + 1010 = 2000 операций копирования. После чего для слияния с selection — ещё 2000 + 100 копирований. Итого при таком подходе всего копирований будет 2000 + 2100 = 4100.
Давайте применим здесь оптимизацию. Сначала сливаем selection и restFirst в массив selection. Операций копирования: 100 + 990 = 1090. Далее сливаем массивы selection и restSecond на что потратим ещё 1090 + 1010 = 2100 копирований. Суммарно выйдет 2100 + 1090 = 3190, что почти на четверть меньше, нежели при предыдущем подходе.
Финальное слияние массивов
int* part2;
int part2Len;
if (selectionLen < restFirstLen) {
glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst
selectionLen += restFirstLen;
part2 = restSecond;
part2Len = restSecondLen;
}
else {
glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond
part2Len = restFirstLen + restSecondLen;
}
glueDelete(arr, selection, selectionLen, part2, part2Len);
Как видим, если нам выгодней сливать selection с restFirst, то мы так и делаем. Иначе мы сливаем как в «restFull»
/// works only if arr is pointer assigned by new keyword
void newGenerationSort(int*& arr, int len) {
int localCatchUp = min(catchUp, len); // потому что мы не можем пытаться вставлять элемент за границами массива
insertionSort(arr, 0, localCatchUp - 1); // для начала сортируем первые localCatchUp элементов
if (len <= localCatchUp) // на случай если это массив на n <= catchUp элементов
return; // а также это база рекурсии
int* selection = new int[len << 1]; // то же что и new int[len * 2]
int left = len - 1; // индекс для хранения новых минимальных элементов
int right = len; // индекс для хранения новых максимальных элементов
selection[left--] = arr[0];
for (int i = 1; i < localCatchUp; ++i) {
selection[right++] = arr[i];
}
int restLen = len >> 1;
int* restFirst = new int[restLen];
int* restSecond = new int[restLen];
int restFirstLen = 0;
int restSecondLen = 0;
for (int i = localCatchUp; i < len; ++i) {
if (selection[right - localCatchUp] <= arr[i])
{
selection[right] = arr[i];
for (int j = right; selection[j - 1] > selection[j]; --j)
swap(selection[j - 1], selection[j]);
++right;
continue;
}
if (selection[left + localCatchUp] >= arr[i])
{
selection[left] = arr[i];
for (int j = left; selection[j] >= selection[j + 1]; ++j)
swap(selection[j], selection[j + 1]);
--left;
continue;
}
if (i & 1) { // i - непарное
restFirst[restFirstLen++] = arr[i];
}
else {
restSecond[restSecondLen++] = arr[i];
}
}
delete[] arr;
int selectionLen = right - left - 1; // просто длина нашей выборки
int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); // копируем все элементы выборки в новый массив
delete[] selection; // удаляем массив размером 2 * len элементов и
selection = copy; // вместо него используем ровно столько памяти, сколько нужно
newGenerationSort(restFirst, restFirstLen);
newGenerationSort(restSecond, restSecondLen);
int* part2;
int part2Len;
if (selectionLen < restFirstLen) {
glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst
selectionLen += restFirstLen;
part2 = restSecond;
part2Len = restSecondLen;
}
else {
glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond
part2Len = restFirstLen + restSecondLen;
}
glueDelete(arr, selection, selectionLen, part2, part2Len);
}
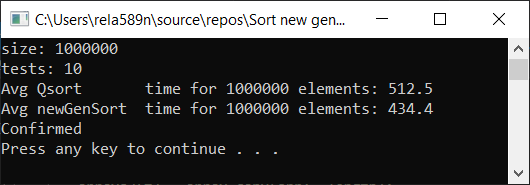
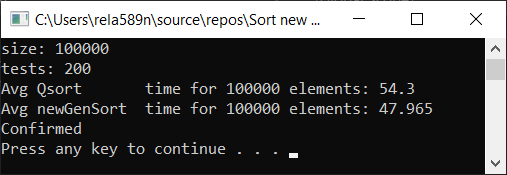
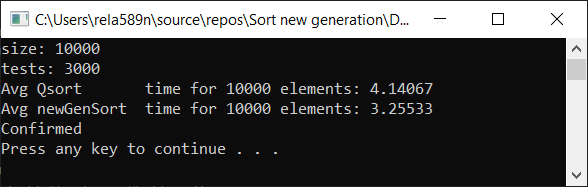
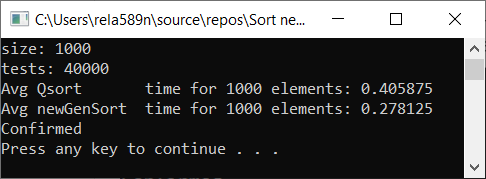
Теперь время тестирования
#include <iostream>
#include <ctime>
#include <vector>
#include <algorithm>
#include "time_utilities.h"
#include "sort_utilities.h"
using namespace std;
using namespace rela589n;
void printArr(int* arr, int len) {
for (int i = 0; i < len; ++i) {
cout << arr[i] << " ";
}
cout << endl;
}
bool arraysEqual(int* arr1, int* arr2, int len) {
for (int i = 0; i < len; ++i) {
if (arr1[i] != arr2[i]) {
return false;
}
}
return true;
}
int* createArray(int length) {
int* a1 = new int[length];
for (int i = 0; i < length; i++) {
a1[i] = rand();
//a1[i] = (i + 1) % (length / 4);
}
return a1;
}
int* array_copy(int* arr, int length) {
int* a2 = new int[length];
for (int i = 0; i < length; i++) {
a2[i] = arr[i];
}
return a2;
}
void tester(int tests, int length) {
double t1, t2;
int** arrays1 = new int* [tests];
int** arrays2 = new int* [tests];
for (int t = 0; t < tests; ++t) { // просто заполнение массивов
int* arr1 = createArray(length);
arrays1[t] = arr1;
arrays2[t] = array_copy(arr1, length);
}
t1 = getCPUTime();
for (int t = 0; t < tests; ++t) {
quickSort(arrays1[t], 0, length - 1);
}
t2 = getCPUTime();
cout << "Avg Qsort time for " << length << " elements: " << (t2 - t1) * 1000 / tests << endl;
int portion = catchUp = 8;
t1 = getCPUTime();
for (int t = 0; t < tests; ++t) {
newGenerationSort(arrays2[t], length);
}
t2 = getCPUTime();
cout << "Avg newGenSort time for " << length << " elements: " << (t2 - t1) * 1000 / tests //<< " Catch up coef: "<< portion
<< endl;
bool confirmed = true; // проверяем идентичны ли массивы
for (int t = 0; t < tests; ++t) {
if (!arraysEqual(arrays1[t], arrays2[t], length)) {
confirmed = false;
break;
}
}
if (confirmed) {
cout << "Confirmed" << endl;
}
else {
cout << "Review your code! Something wrong..." << endl;
}
}
int main() {
srand(time(NULL));
int length;
double t1, t2;
cout << "size: ";
cin >> length;
int t;
cout << "tests: ";
cin >> t;
tester(t, length);
system("pause");
return 0;
}
Небольшая ремарка: я использовал именно эту реализацию quickSort для того, чтобы всё было честно. Стандартная sort из библиотеки algorithm хотя и универсальна, но работает в 2 раза медленней представленной ниже.
// [min, max]
int random(int min, int max) {
return min + rand() % ((max + 1) - min);
}
void quickSort(int * arr, int b, int e)
{
int l = b, r = e;
int piv = arr[random(l, r)];
while (l <= r)
{
for (; arr[l] < piv; ++l);
for (; arr[r] > piv; --r);
if (l <= r)
swap(arr[l++], arr[r--]);
}
if (b < r)
quickSort(arr, b, r);
if (e > l)
quickSort(arr, l, e);
}
Все тесты были проведены на машине на проц. Intel core i3 7100u и 8ГБ ОЗУ
a1[i] = rand();
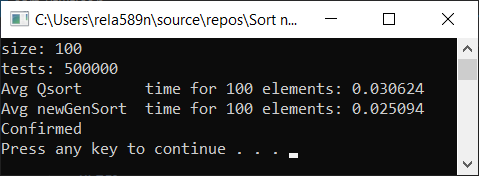
a1[i] = (i + 1) % (length / 4);
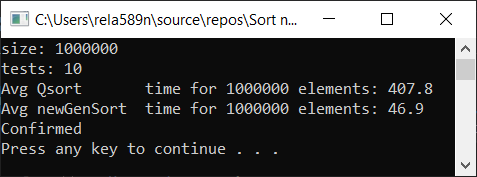
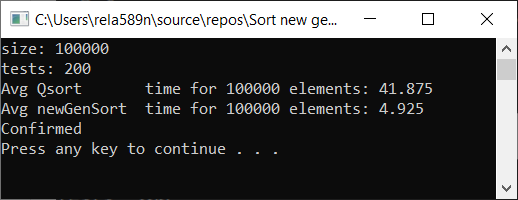
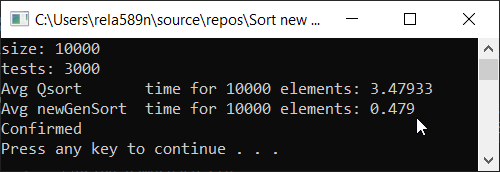
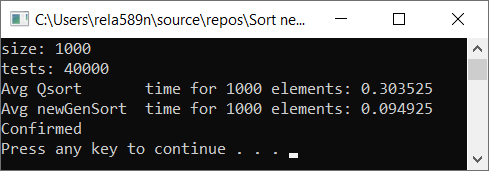
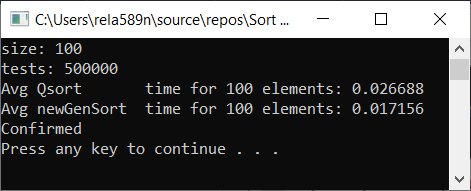
a1[i] = (i + 1);
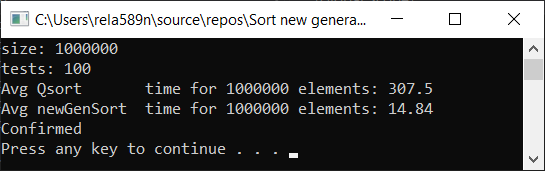
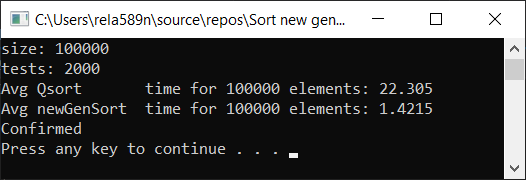
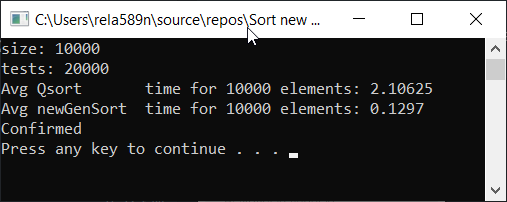
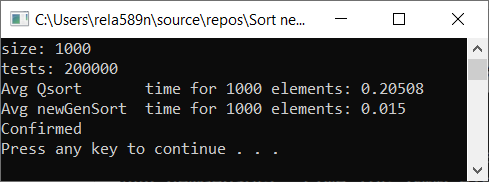
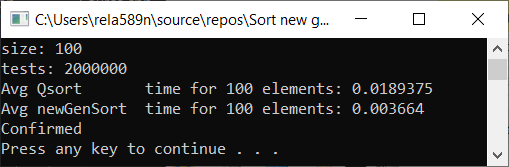
Выводы
Как видим, алгоритм работает, и работает хорошо. По крайней мере всё чего мы хотели, было достигнуто. На счёт стабильности, не уверен, не проверял. Можете сами проверить. Но по-идее она должна достигаться очень легко. Просто в некоторых местах вместо знака > поставить ≥ или что-то того.
Автор: Сидельник Евгений