В издательстве “ДМК Пресс” вышла книга “Олимпиадное программирование” с подзаголовком “Изучение и улучшение алгоритмов на соревнованиях”. Она стала глотком свежего воздуха для всех, кто интересуется, готовит и готовится к участию, или только планирует в будущем, в таком интеллектуальном виде деятельности, как различные мероприятия спортивного программирования. В России с ними знакомы недостаточно.
Российское издание книги “Guide to Competitive Programming” (издательство Springer International Publishing AG)вышло при поддержке Центра развития ИТ-образования МФТИ и его руководителя Алексея Малеева, Mail.Ru Group, а также проекта Moscow Workshops ICPC.

«Олимпиадное программирование с каждым годом становится все более популярным среди шольников и студентов. Отличным примером этому стало то, что в 2019 году мы, Moscow Workshops ICPC, в ноябре мы проведем уже десятые сборы по подготовке к чемпионату мира в самых разных точках земного шара, они уже прошли в Сингапуре, и Европае и Южной Америке, и России — от Владивостока до Москвы. В начале октября в Москве прошел Moscow Programming Contest, участие в котором приняли 2284 человека на 18 площадках московских вузов — это абсолютный рекорд по масштабу соревнования, который состоялся при поддержке Росмолодежи.
Мы очень рады столь живому интересу ребят, и готовы всячески его поддерживать — например, для студентов московских вузов мы проводим бесплатную подготовку к ICPC с участием самых лучших тренеров. И, конечно, закрепить материал, разобрать задания, подтянуть свои знания участникам всегда полезно. Поэтому я очень рад, что появилась ваша книга, и всех нас с этим поздравляю. Надеемся, что на финале ICPC в Москве в июне 2020 года будут уже те ребята, которые ее прочтут и станут героями второго, дополненного издания».
Алексей Малеев, Директор финала чемпионата мира ICPC 2020 в Москве, проректор МФТИ, основатель проекта Moscow Workshops ICPC.
На русский язык “Guide to Competitive Programming” была переведена с английского. Кроме английского и русского языка, увидело свет издание на корейском языке.
Автор книги — Антти Лааксонен, преподаватель и исследователь из Хельсинского университета Аалто (Финляндия) [3] с большим опытом преподавания программирования и алгоритмов, тренер команды Финляндии на международных соревнованиях по программированию. Он имеет высокий рейтинг 2347 и статус “международный мастер” на портале Codeforces под ником “pllk” [4]. В 2008 году он А. Лааксонен стал одним из организаторов олимпиады по информатике в своей стране. В 2016 — научным руководителем Балтийской олимпиады по информатике.
Целевой аудиторией книги являются все интересующиеся и/или работающие в сфере олимпиадного программирования. Но, для полноценного усвоения материала потребуется знание основ программирования, при этом автор не требует от читателя опыта проектирования алгоритмов и участия в олимпиадах. Все это позволяет рекомендовать данную работу достаточно широкому кругу заинтересованных читателей. Для начинающих она станет введением в современное олимпиадное программирование, опытным специалистам поможет систематизировать знания, станет для них справочным пособием.
Подача материала в книге осуществляется от простого к сложному. Вначале знакомится с целями и задачами книги, с олимпиадным программированием, сборником задач CSES [5] и прочими актуальными книгами по олимпиадному программированию.
Получив необходимую теоретическую базу читатель будет готов перейти к практике. Техника программирования — следующая тема. В нее автор включил основы языка С++ (стандарт С11), на котором реализованы все примеры в книге; разбор рекурсивных алгоритмов и поразрядных операций.
В главах книги читатель сможет найти информацию о большинстве “стандартных” тем и примеров реализации алгоритмов, которые предлагаются участникам олимпиад по программированию: структуры данных, динамическое программирование, графовые алгоритмы и алгоритмы на деревьях, запросы по диапазону, работа со строками.
Отдельно хотелось бы выделить ряд глав книги. Например, глава «Избранные вопросы проектирования алгоритмов». В нее вошли алгоритмы с параллельным просмотром разрядов, амортизационный анализ, нахождение минимальных значений. Читателю предлагаются алгоритмы нахождения расстояния Хэмминга, решение задачи на достижимость в графах, метод двух указателей, троичный поиск, минимизация сумм и другие интереснейшие темы для “олимпиадников” и их тренеров.
В качестве примера, приведу пример задач из главы “Избранные вопросы проектирования алгоритмов”.
Рассмотрим алгоритмы с параллельным просмотром разрядов, в которых для эффективной обработки данных используются поразрядные операции. В типичном случае мы можем заменить цикл for поразрядными операциями, что существенно уменьшает время работы алгоритма.
Алгоритмы с параллельным просмотром разрядов
Алгоритмы с параллельным просмотром разрядов основаны на том факте, что отдельными разрядами числа можно манипулировать параллельно, применяя поразрядные операции. Поэтому один из способов проектирования алгоритмов – представить шаги алгоритма таким образом, чтобы их можно было эффективно реализовать с помощью поразрядных операций.
Расстояние Хэмминга Расстоянием Хэмминга
hamming(a, b) между строками a и b одинаковой длины называется количество позиций, в которых эти строки различаются. Например:
hamming(01101, 11001) = 2.
Рассмотрим следующую задачу: дано n битовых строк длины k, вычислить минимальное расстояние Хэмминга между двумя строками. Например, для строк [00111, 01101, 11110] ответом будет 2, потому что
- hamming(00111, 01101) = 2;
- hamming(00111, 11110) = 3;
- hamming(01101, 11110) = 3.
Задачу можно решить «в лоб», вычислив расстояние Хэмминга между каждыми двумя строками. Временная сложность такого алгоритма равна (n
k). Для вычисления расстояния между строками a и b служит следующая функция:
int hamming(string a, string b) {
int d = 0
for (int i = 0; i < k; i++) {
if (a[i] != b[i]) d++;
}
return d;
}
Но поскольку строки состоят из бит, решение можно оптимизировать, если хранить строки в виде целых чисел и вычислять расстояние между ними с помощью поразрядных операций. В частности, если k ≤ 32, то строки можно хранить как значения типа int и для вычисления расстояния использовать такую функцию:
int hamming(int a, int b) {
return __builtin_popcount(a^b);
}
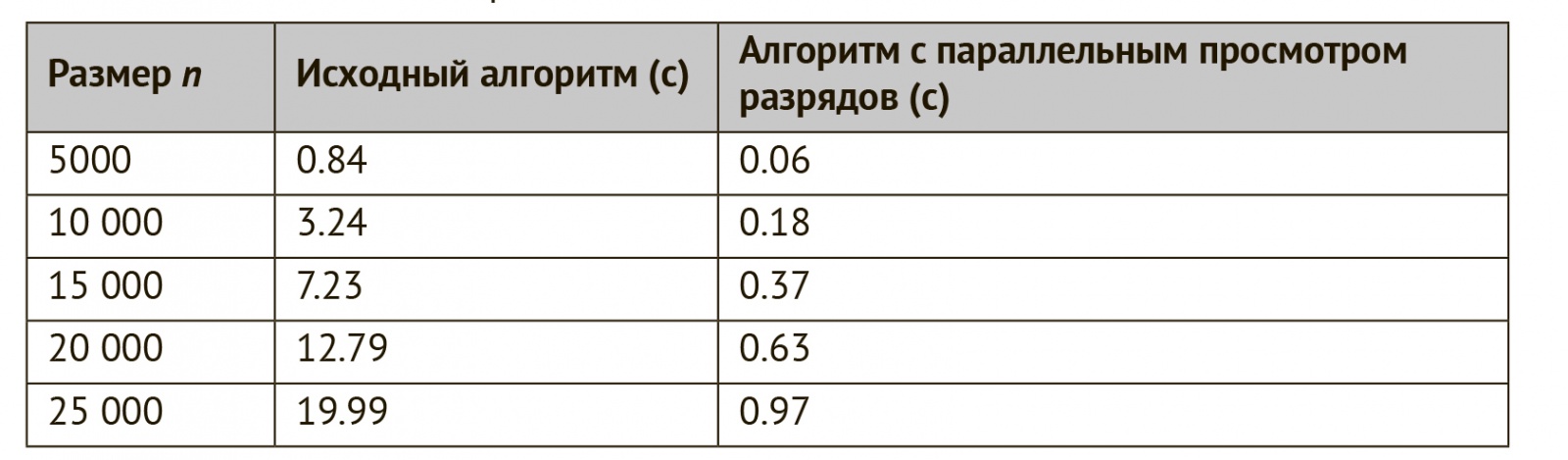
Здесь операция ИСКЛЮЧАЮЩЕЕ ИЛИ строит строку, в которой единицы находятся в тех позициях, где a и b различаются. Затем число единичных разрядов вычисляется функцией __builtin_popcount. В таблице приведены результаты сравнения исходного алгоритма и алгоритма с параллельным просмотром разрядов с точки зрения времени выполнения на современном компьютере. Алгоритм с параллельным просмотром разрядов оказался примерно в 20 раз быстрее.
Таблица: Время работы алгоритмов, вычисляющих минимальное расстояние Хэмминга для n битовых строк длины k = 30
Не меньшего внимания заслуживают главы “Математика” и “Геометрия”. Как читатель уже догадался, они посвящены решению математических и геометрических задач средствами языка программирования С++ и построению соответствующих алгоритмов. В “математической” главе нас ждет пять больших тем: “Теория чисел”, “Комбинаторика”, “Матрицы”, “Вероятность” и “Теория игр”. А в “геометрической”: “Технические средства в геометрии”, “Алгоритмы на основе заметающей прямой”. Таким образом, комплексная подача построения алгоритмов для решения математических и геометрических задач, делает книгу “находкой” для “олимпиадников”, ведь на фоне дефицита книг по данной тематике, это большая редкость.
Ряд проблем, автор решил поместить в главу “Дополнительные темы”. Их освоение “ иногда может помочь при решении наиболее трудных олимпиадных задач”. Это “Квадратный корень в алгоритмах”, “И снова о деревьях отрезков”, “Дучи”, “Оптимизация динамического программирования” и “Разное”. Исходя из названия дополнительного пояснения требуют подглавы о деревьях отрезков и о разном.
Что касается деревьев отрезков, то читатель познакомится с ленивым распространением, динамическими деревьями, структурами данных в вершинах, двумерными деревьями. А в “Разном” его ждет: встреча в середине (разбиение пространства поиска на две части, приблизительно равные, выполнение поиска в каждой из частей, а далее объединение результатов), подсчет множеств, параллельный двоичный поиск, динамическая связность.
Завершают книгу справочные сведения по математике и обширная библиография (32 источника).
Итак, книга “Олимпиадное программирование” Антти Лааксоненена отличное введение в мир спортивного программирования. Одновременно и замечательное справочное пособие. Книга подойдет начинающим “олимпиадникам” и поможет в систематизировании знаний опытным. Будет полезна и тренерам.
Еще раз отметим, что все примеры в книге реализованы на языке программирования C++. Он наиболее востребован на олимпиадах. Но кто-то может посчитать это недостатком книги, ведь популярны и другие языки — Python, Java. Те, кто предпочитают эти языки программирования, могут решить предложенные задачи в книге на своем любимом языке. Это будет неплохой тренировкой. В конечном итоге, именно в поиске оптимального решения и заключается выполнение олимпиадных задач.
Статью подготовил: Игорь Штомпель, автор и ведущий рубрики «Карьера Образование» в журнале «Системный администратор»
Автор: miptru







