Благодарим автора блога Антона Екименко за его доклад
Введение
Эта заметка написана по следам конференции Wolfram Russian Technology Conference и содержит конспект доклада, с которым я выступал. Мероприятие состоялось в июне в городе Санкт-Петербурге. Учитывая то, что работаю я в квартале от места проведения конференции, я не мог не посетить это событие. В 2016 и 2017 годах я слушал доклады конференции, а в этом году выступил с докладом. Во–первых, появилась интересная (как мне кажется) тема, которую мы развиваем с Кириллом Беловым, а во-вторых, после длительного изучения законодательства РФ в части санкционной политики, на предприятии, где я тружусь появилось аж целых две лицензии Wolfram Mathematica.
Прежде, чем перейти к теме моего выступления я бы хотел отметить хорошую организацию мероприятия. На визитной страничке конференции используется изображение Казанского собора. Собор является одной из главных достопримечательностей Петербурга и его очень хорошо видно из зала, в котором проходила конференция.

На входе в СПбГЭУ участников встречали помощники из числа студентов – не позволяли заблудиться. Во время регистрации выдавались небольшие сувенирчики (игрушка – мигающий спайки, ручка, наклейки с символикой Wolfram). Обед и кофе-брейк также были включены в расписание конференции. Про вкусный кофе и пирожочки я уже отмечал на стене группы – повара молодцы. Этой вводной частью я бы хотел подчеркнуть, что само мероприятие, его формат и место проведения уже приносят положительные эмоции.
Доклад, который был подготовлен мною и Кириллом Беловым называется «Использование Wolfram Mathematica для решения задач прикладной геофизики. Спектральный анализ сейсмических данных или «куда бежали древние реки». Содержание доклада покрывает две части: во-первых, это использование алгоритмов, имеющихся в Wolfram Mathematica для анализа геофизических данных, а во-вторых, это то как геофизические данные поместить в Wolfram Mathematica.
Сейсморазведка
Для начала нужно сделать небольшой экскурс в геофизику. Геофизика — это наука, изучающая физические свойства горных пород. Ну а поскольку породы имеют разные свойства: электрические, магнитные, упругие, то существуют соответствующие методы геофизики: электроразведка, магниторазведка, сейсморазведка… В контексте данной статьи подробнее затронем только сейсмическую разведку. Сейсморазведка является основным методом поиска нефти и газа. Метод основан на возбуждении упругих колебаний и последующей регистрации отклика от горных пород слагающих исследуемую территорию. Возбуждение колебаний осуществляется на суше (динамитом или невзрывными вибрационными источниками упругих колебаний) или на море (пневмопушками). Упругие колебания распространяются через толщу горных пород преломляясь и отражаясь на границах слоёв с разными свойствами. Отражённые волны возвращаются на поверхность и регистрируются геофонами на суше (как правило это электродинамические приборы, основанные на движении магнита, подвешенного в катушке) или гидрофонами в море (основаны на пьезоэффекте). По времени прихода волн можно судить о глубинах геологических слоёв.
Сейсмическое судно буксирует оборудование

Пневмопушка возбуждает упругие колебания

Волны проходят через толщу горных пород и регистрируются гидрофонами

Научно-исследовательское судно геофизической разведки «Иван Губкин» на причале у Благовещенского моста в Петербурге

Модель сейсмического сигнала
Горные породы имеют разные физические свойства. Для сейсморазведки прежде всего важны упругие свойства — скорость распространения упругих колебаний и плотность. Если два слоя будут иметь одинаковые или близкие свойства то волна «не заметит» границу между ними. Если же скорости волн в слоях будут отличаться, то на границе слоёв возникнет отражение. Чем больше разница в свойствах тем интенсивнее отражение. Его интенсивность будет определяться коэффициентом отражения (rc):
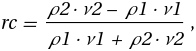
где ρ — плотность пород, ν — скорость волн, 1 и 2 обозначают верхний и нижний слои.
Одной из наиболее простых и часто используемых моделей сейсмического сигнала является свёрточная модель, когда зарегистрированная сейсмическая трасса представляется, как результат свёртки последовательности коэффициентов отражения с зондирующим импульсом:
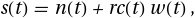
где s(t) — сейсмическая трасса, т.е. все что записал гидрофон или геофон в течение фиксированного времени регистрации, w(t) — сигнал, который генерирует пневмопушка, n(t) — случайный шум.
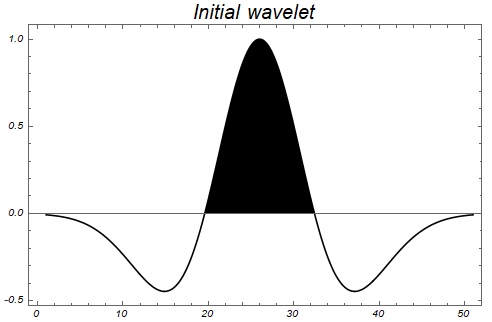
Рассчитаем для примера синтетическую сейсмотрассу. В качестве исходного сигнала будем использовать широко используемый в сейсморазведке импульс Риккера.
length=0.050; (*Signal lenght*)
dt=0.001;(*Sample rate of signal*)
t=Range[-length/2,(length)/2,dt];(*Signal time*)
f=35;(*Central frequency*)
wavelet=(1.0-2.0*(Pi^2)*(f^2)*(t^2))*Exp[-(Pi^2)*(f^2)*(t^2)];
ListLinePlot[wavelet, Frame->True,PlotRange->Full,Filling->Axis,PlotStyle->Black,
PlotLabel->Style["Initial wavelet",Black,20],
LabelStyle->Directive[Black,Italic],
FillingStyle->{White,Black},ImageSize->Large,InterpolationOrder->2]Исходный сейсмический импульс
Две границы зададим на глубинах 300 мс и 600 мс, а коэффициенты отражения будут случайными числами
rcExample=ConstantArray[0,1000];
rcExample[[300]]=RandomReal[{-1,0}];
rcExample[[600]]=RandomReal[{0,1}];
ListPlot[rcExample,Filling->0,Frame->True,Axes->False,PlotStyle->Black,
PlotLabel->Style["Reflection Coefficients",Black,20],
LabelStyle->Directive[Black,Italic]]Последовательность коэффициентов отражения
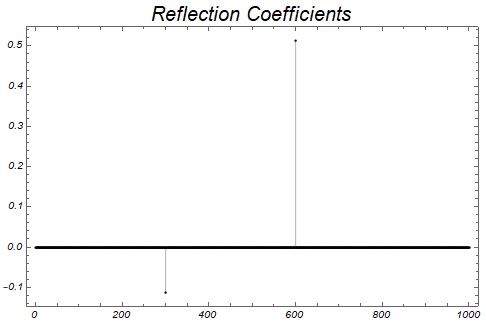
Рассчитаем и отобразим сейсмическую трассу. Поскольку коэффициенты отражения имеют разные знаки, то и на сейсмической трассе получаем два знакопеременных отражения.
traceExamle=ListConvolve[wavelet[[1;;;;1]],rcExample];
ListPlot[traceExamle,
PlotStyle->Black,Filling->0,Frame->True,Axes->False,
PlotLabel->Style["Seismic trace",Black,20],
LabelStyle->Directive[Black,Italic]]Смоделированная трасса
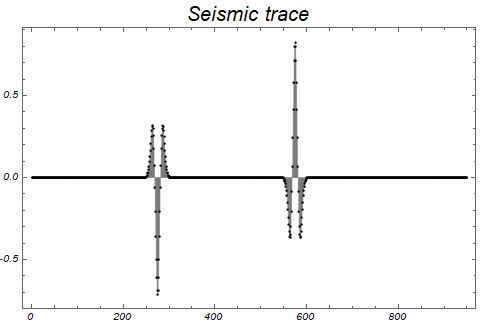
Для данного примера нужно сделать оговорку — в действительности глубина пластов определяется конечно в метрах, а расчёт сейсмической трассы происходит для временной области. Правильнее было бы задать глубины в метрах и рассчитать времена прихода зная скорости в пластах. В данном случае я сразу задал пласты на временной оси.
Если говорить о полевых исследованиях, то в результате таких наблюдений регистрируется огромное количество подобных временных рядов (сейсмических трасс). Например, при исследовании участка длиной 25 км и шириной 15 км, где в результате работ каждая трасса характеризует ячейку размером 25х25 метров (такая ячейка называется бин), финальный массив данных будет содержать 600000 трасс. При шаге дискретизации по времени равном 1 мс, времени записи 5 секунд окончательный файл данных составит более 11 Гб, а объём исходного «сырого» материала может составить сотни гигабайт.
Как работать с ними в Wolfram Mathematica?
Пакет GeologyIO
Началом разработки пакета стал вопрос на стене VK группы русскоязычной поддержки. Благодаря ответам сообщества решение было найдено очень быстро. И в результате переросло в серьёзную разработку. Соответствующий пост на стене Wolfram Comunity даже был отмечен модераторами. На текущий момент пакет поддерживает работу со следующими типами данных, которые активно используются в геологической отрасли:
- импорт картографических данных формата ZMAP и IRAP
- импорт измерений в скважинах формата LAS
- ввод и вывод сейсмических файлов формата SEGY
Чтобы установить пакет необходимо следовать инструкциям на странице загрузки собранного пакета, т.е. выполнить следующий код в любом блокноте Mathematica:
If[PacletInformation["GeologyIO"] === {}, PacletInstall[URLDownload[
"https://wolfr.am/FiQ5oFih",
FileNameJoin[{CreateDirectory[], "GeologyIO-0.2.2.paclet"}]
]]]После чего пакет установится в папку по умолчанию, путь к которой можно получить следующим образом:
FileNameJoin[{$UserBasePacletsDirectory, "Repository"}]Для примера продемонстрируем основные возможности пакета. Вызов осуществляется традиционно для пакетов в Wolfram Language:
Get["GeologyIO`"]Пакет разрабатывается с использованием Wolfram Workbench. Это позволяет сопроводить основной функционал пакета документацией, которая по формату представления не отличается от документации самой Wolfram Mathematica и снабдить пакет тестовыми файлами для первого знакомства.
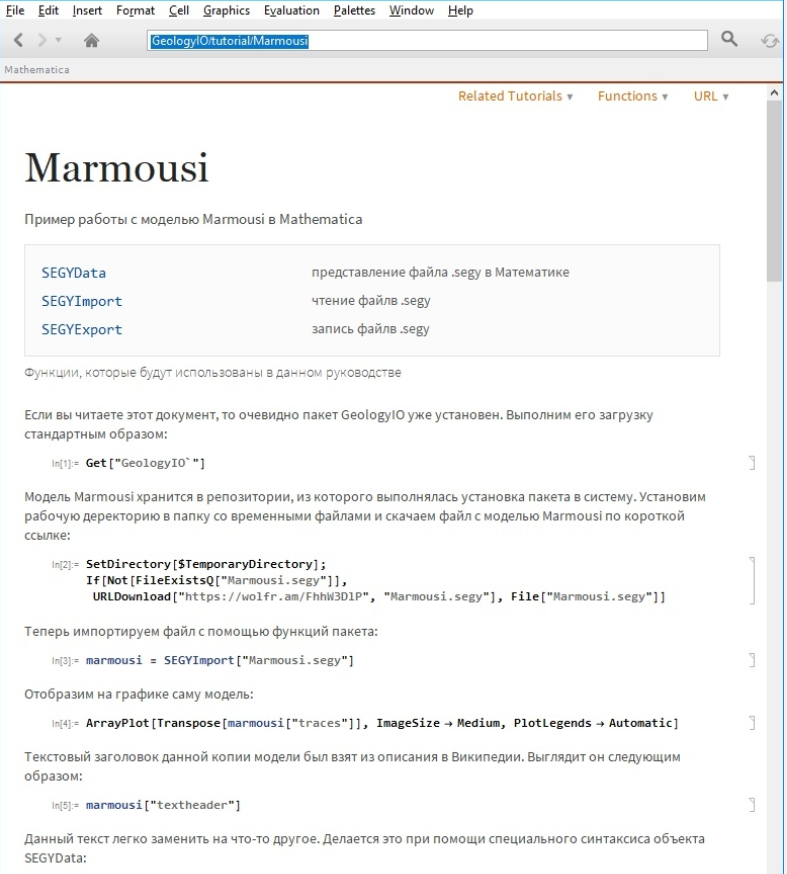
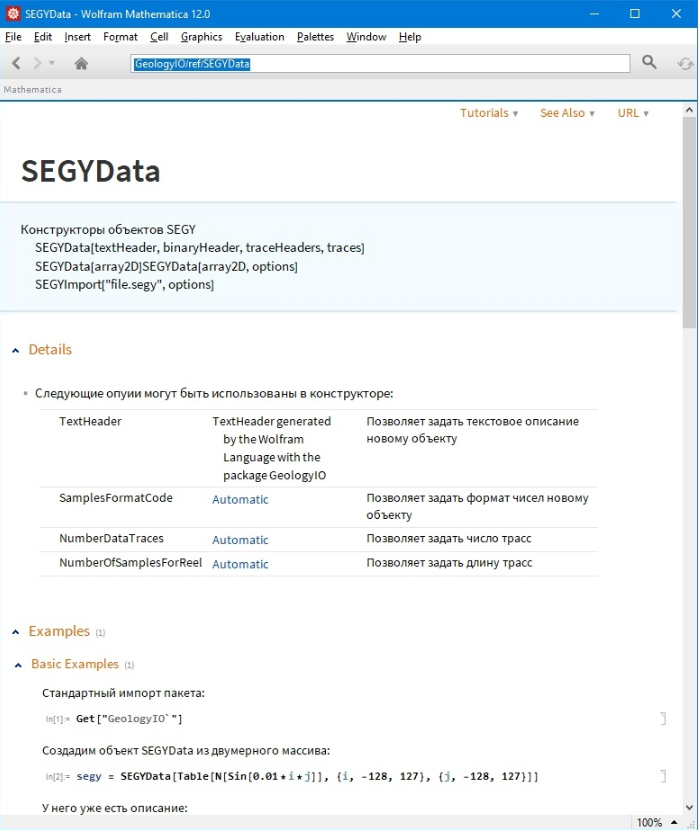
Таким файлом, в частности является файл «Marmousi.segy»- это синтетическая модель геологического разреза, которую разработал французский институт нефти. Используя эту модель разработчики тестирую собственные алгоритмы моделирования волнового поля, обработки данных, инверсии сейсмических трасс и т.д. Сама модель Marmousi хранится в репозитории, откуда был скачан сам пакет. Для того, чтобы получить файл — выполним следующий код:
If[Not[FileExistsQ["Marmousi.segy"]],
URLDownload["https://wolfr.am/FiQGh7rk", "Marmousi.segy"];]
marmousi = SEGYImport["Marmousi.segy"]Результат импорта — объект SEGYData

Формат SEGY предполагает хранение разной информации о наблюдениях. Во-первых, это текстовые комментарии. Сюда заносят информацию о месте проведения работ, названия компаний выполнивших измерения и т.д. В нашем случае этот заголовок вызывается запросом с ключом TextHeader. Здесь приведён укороченный текстовый заголовок:
Short[marmousi["TextHeader"]]«The Marmousi data set was generated at the Institute …nimum velocity of 1500 m/s and a maximum of 5500 m/s)»
Отобразить собственно гелогическую модель можно обратившись к сейсмическим трассам по ключу «traces» (одной из фич пакета является независимость ключей от регистра):
ArrayPlot[Transpose[marmousi["traces"]], PlotTheme -> "Detailed"]Модель Marmousi
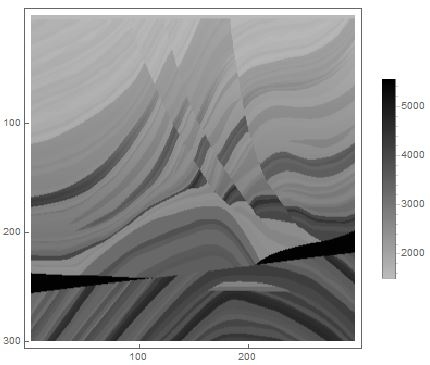
На текущий момент пакет также позволяет загружать данные частями из больших файлов, благодаря чему становится возможно обработка файлов, размер которых может достигать десятков гигабайт. Также в число функций пакета входят функции для экспорта данных в .segy и частичной дозаписи в конец файла.
Отдельно стоит отметить функциональность пакета при работе со сложной структурой .segy-файлов. Так как он позволяет не только обращаться по ключам и индексам к отдельным трассам, заголовкам, но и изменять их с последующей записью в файл. Многие технические детали реализации GeologyIO выходят за рамки этой статьи и, вероятно, заслуживают отдельного описания.
Актуальность спектрального анализа в сейсморазведке
Возможность импорта сейсмических материалов в Wolfram Mathematica позволяет использовать встроенный функционал обработки сигналов для экспериментальных данных. Поскольку каждая сейсмическая трасса представляет собой временной ряд, то одним из основных инструментов их изучения является спектральный анализ. Среди предпосылок анализу частотного состава сейсмических данных можно назвать, например, следующие:
- Разные типы волн характеризуются разным частотным составом. Это позволяет выделить полезные волны и подавить волны-помехи.
- Такие свойства горных пород, как пористость и насыщенность могут влиять на частотный состав. Это позволяет выделять горные породы с лучшими свойствами.
- Слои с разной толщиной обуславливают аномалии в разных частотных диапазонах.
Третий пункт является основным в контексте данной статьи. Ниже приведён фрагмент кода для расчета сейсмических трасс в случае слоя с меняющейся толщиной — модель клина. Эта модель традиционно изучается в сейсморазведке для анлиза интерференционных эффектов, когда волны отраженные от многих слоёв накладываются друг на друга.
nx=200;(* Number of grid points in X direction*)
ny=200;(* Number of grid points in Y direction*)
T=2;(*Total propagation time*)
(*Velocity and density*)
modellv=Table[4000,{i,1,ny},{j,1,nx}];(* P-wave velocity in m/s*)
rho=Table[2200,{i,1,ny},{j,1,nx}];(* Density in g/cm^3, used constant density*)
Table[modellv[[150-Round[i*0.5];;,i]]=4500;,{i,1,200}];
Table[modellv[[;;70,i]]=4500;,{i,1,200}];
(*Plotting model*)
MatrixPlot[modellv,PlotLabel->Style["Model of layer",Black,20],
LabelStyle->Directive[Black,Italic]]Модель выклинивающегося пласта
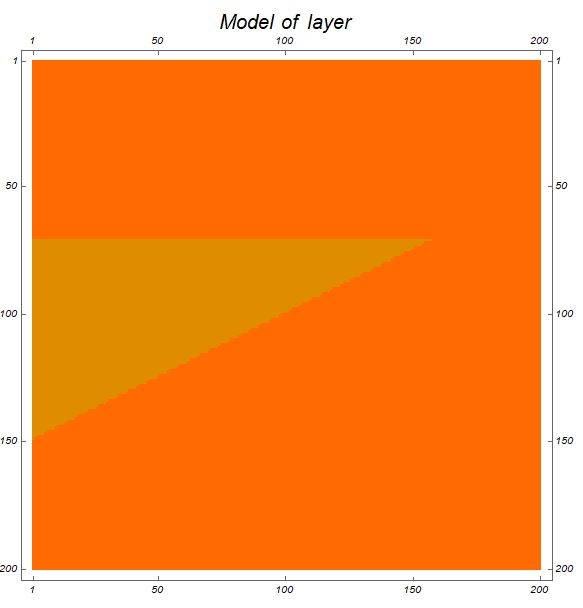
Скрость волн внутри клина составляет 4500 м/с, вне клина 4000м/с, а плотность принята постоянной 2200 г/см³. Для такой модели рассчитаем коэффиценты отражения и сейсмические трассы.
rc=Table[N[(modellv[[All,i]]-PadLeft[modellv[[All,i]],201,4000][[1;;200]])/(modellv[[All,i]]+PadLeft[modellv[[All,i]],201,4500][[1;;200]])],{i,1,200}];
traces=Table[ListConvolve[wavelet[[1;;;;1]],rc[[i]]],{i,1,200}];
starttrace=10;
endtrace=200;
steptrace=10;
trasenum=Range[starttrace,endtrace,steptrace];
traserenum=Range[Length@trasenum];
tracedist=0.5;
Rotate[Show[
Reverse[Table[
ListLinePlot[traces[[trasenum[[i]]]]*50+trasenum[[i]]*tracedist,Filling->{1->{trasenum[[i]]*tracedist,{RGBColor[0.97,0.93,0.68],Black}}},PlotStyle->Directive[Gray,Thin],PlotRange->Full,InterpolationOrder->2,Axes->False,Background->RGBColor[0.97,0.93,0.68]],
{i,1,Length@trasenum}]],ListLinePlot[Transpose[{ConstantArray[45,80],Range[80]}],PlotStyle->Red],PlotRange->All,Frame->True],270Degree]Сейсмические трассы для модели клина
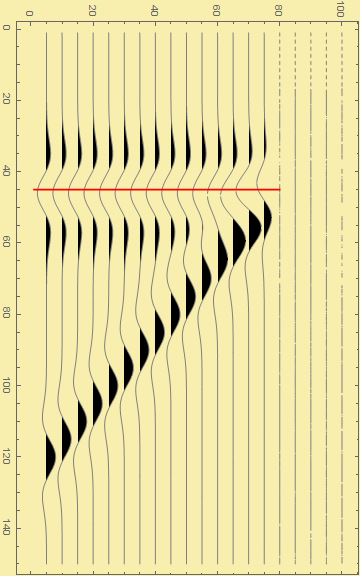
Последовательность сейсмических трасс изображенная на этом рисунке называется сейсмическим разрезом. Как можно заметить, его интерпретация может выполняться и на интуитивном уровне, поскольку геометрия отражённых волн однозначно соответствует модели, которая была задана ранее. Если более детально анализировать трассы, то можно заметить, что трассы с 1-й по, примерно, 30-ю не отличаются — отражение от кровли пласта и от подошвы не накладываются друг на друга. Начиная с 31-й трассы отражения начинают интерферировать. И, хотя, в модели коэффициенты отражения не меняются по горизонтали — сейсмические трассы меняют свою интенсивность при изменении толщины пласта.
Рассмотрим амплитуду отражения от верхней границы пласта. Начиная с 60-й трассы интенсивность отражения начинает возрастать и на 70-й трассе становится максимальной. Так проявляется интерференция волн от кровли и подошвы для пластов, приводя в некторых случаях к существенным аномалиям сейсмической записи.
ListLinePlot[GaussianFilter[Abs[traces[[All,46]]],3][[;;;;2]],
InterpolationOrder->2,Frame->True,PlotStyle->Black,
PlotLabel->Style["Amplitude of reflection",Black,20],
LabelStyle->Directive[Black,Italic],
PlotRange->All]График амплитуды отражённой волны от верхней кромки клина
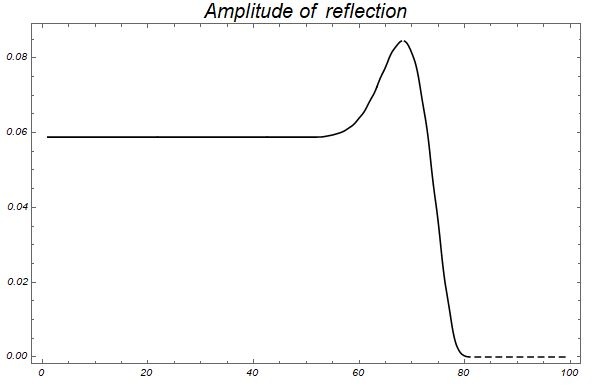
Логично, что когда сигнал более низкочастотный, то интерференция начинает проявлятся при больших толщинах пласта, а в случае высокочастотного сигнала интерфренция возникает при меньших толщинах. Следующий фрагмент кода создаёт сигнал с частотами 35 Гц, 55 Гц и 85 Гц.
waveletSet=Table[(1.0-2.0*(Pi^2)*(f^2)*(t^2))*Exp[-(Pi^2)*(f^2)*(t^2)],
{f,{35,55,85}}];
ListLinePlot[waveletSet,PlotRange->Full,PlotStyle->Black,Frame->True,
PlotLabel->Style["Set of wavelets",Black,20],
LabelStyle->Directive[Black,Italic],
ImageSize->Large,InterpolationOrder->2]Набор исходных сигналов с частотами 35 Гц, 55Гц, 85Гц
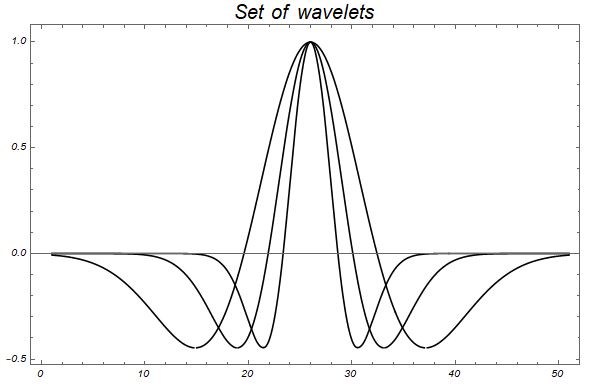
Выполнив расчет сейсмических трасс и построив графики амплитуд отражённой волны, мы можем увидеть, что для разных частот аномалия наблюдается при разных толщинах пласта.
tracesSet=Table[ListConvolve[waveletSet[[j]][[1;;;;1]],rc[[i]]],{j,1,3},{i,1,200}];
lowFreq=ListLinePlot[GaussianFilter[Abs[tracesSet[[1]][[All,46]]],3][[;;;;2]],InterpolationOrder->2,PlotStyle->Black,PlotRange->All];
medFreq=ListLinePlot[GaussianFilter[Abs[tracesSet[[2]][[All,46]]],3][[;;;;2]],InterpolationOrder->2,PlotStyle->Black,PlotRange->All];
highFreq=ListLinePlot[GaussianFilter[Abs[tracesSet[[3]][[All,46]]],3][[;;;;2]],InterpolationOrder->2,PlotStyle->Black,PlotRange->All];
Show[lowFreq,medFreq,highFreq,PlotRange->{{0,100},All},
PlotLabel->Style["Amplitudes of reflection",Black,20],
LabelStyle->Directive[Black,Italic],
Frame->True]Графики амплитуд отражённой волны от верхней кромки клина для разных частот
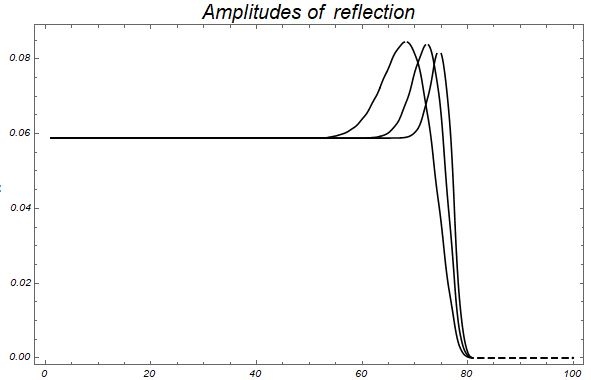
Возможность делать выводы о толщине пласта по результатам сейсмических наблюдений является крайне полезной, ведь одной из главных задач при разведке месторожения нефти является оценка наиболее перспективных точек для заложения скважины (т.е. тех участков, где пласт имеет большую толщину). Помимо этого в геологическом разрезе могут встречаться такие объекты, которые своим генезисом обуславливают резкую смену толщин пласта. Это делает спектральный анализа эффективным инструментом их изучения. В следующей части статьи рассмотрим такие гелогические объекты подробнее.
Экспериментальные данные. Где получены и что в них искать?
Материалы, которые анализируются в статье получены на территории Западной Сибири. Регион, как наверное знают все без исключения, является основным нефтедобывающим регионом нашей страны. Активная разработка меторождений началась в регионе в 60-х года прошлого века. Основным методом поиска месторождений нефти является сейсморазведка. Интересно рассматривать спутниковые снимки этой территории. При малом масштабе можно отметить огромное количество болот и озёр, увеличивая карту можно увидеть кустовые площадки бурения скважин, а увеличив карту до предела можно различить и просеки профилей, по которым выполнялись сейсмические наблюдения.
Спутниковый снимок Яндекс карт — район города Ноябрьск
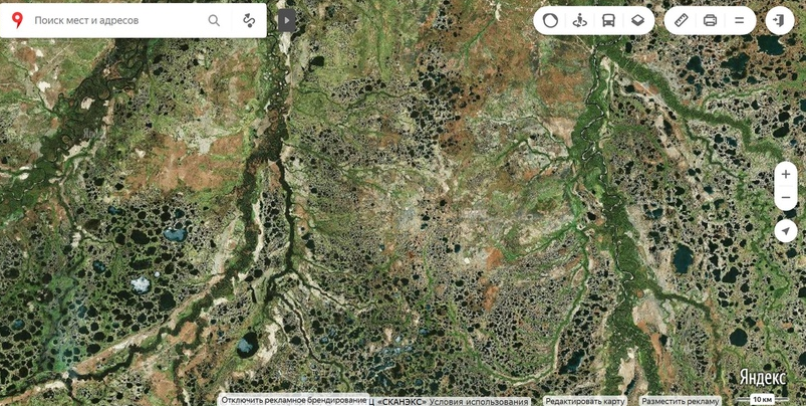
Сеть кустовых площадок на одном из меторождений
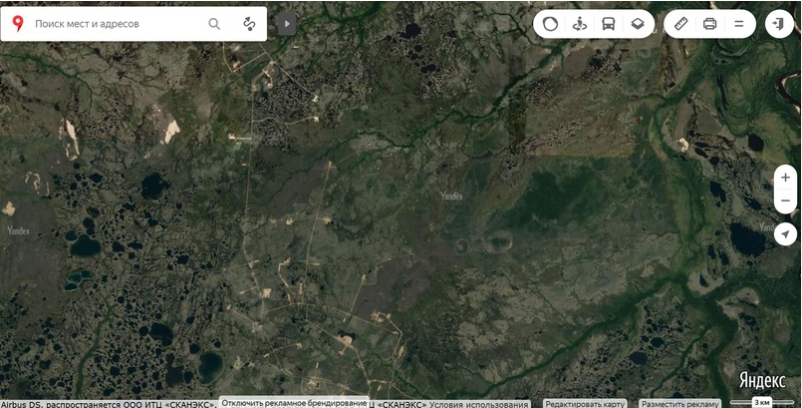
Нефтеносные породы Запаной Сибири залегают в широком диапазоне глубин — от 1км до 5км. Основной объём пород содержащих нефть сформирован в юрское и меловое время. Юрский период наверное многим известен по одноимённому фильму. Климат юрского периода существенно отличался от современного. В энкциклопедии Британника есть серия палеокарт, которые характеризуют каждую гелогическую эпоху.
Настоящее время
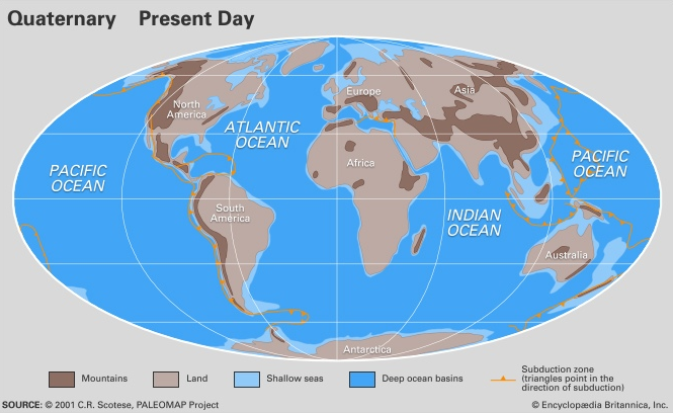
Юрский период
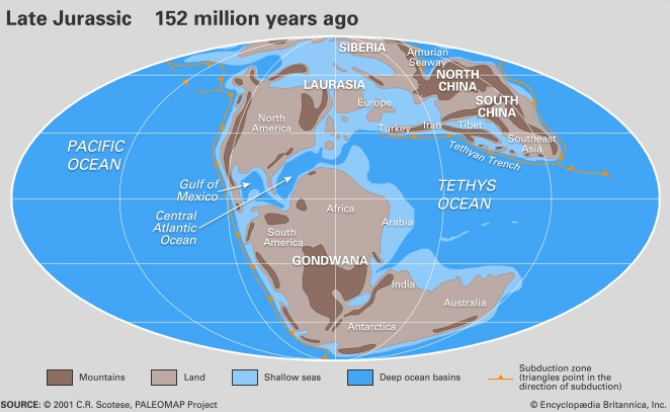
Обратите внимание, что в юрское время территория Западной Сибири предствляла собой морское побережье (суша пересекаемая реками и мелководное море). Поскольку климат был комфортным, можно предположить, что типичный пейзаж того времни выглядел следующим образом:
Сибирь юрского периода

На этой картинке для нас важны не столько звери и птицы, сколько изображение реки на заднем плане. Река — это тот самый гелогический объект, на котором мы останавливались ранее. Дело в том, что деятельность рек позволяет накапливаться хорошо сортированным песчаникам, которые затем станут резервуаром для нефти. Эти резервуары могут иметь причудливую, сложную форму (как и русло реки) и они имеют изменчивую толщину — у берегов толщина мала, а ближе к центру русла или на участках меандр возрастает. Итак, сформированные в юрское время реки сейчас находятся на глубине порядка трёх километров и являются объектом поиска резервуаров нефти.
Экспериментальные данные. Обработка и визуализация
Сделаем сразу оговорку, относительно сейсмических материалов показанных в статье — в силу того, что объём данных использованных для анализа значительный — в текст статьи помещен только фрагмент оригинального набора сейсмических трасс. Это позволит всем желающим воспроизвести приведённые вычисления.
Работая с сейсмическими данными геофизик, как правило использует специализированное программное обеспечение (есть несколько передовиков отрасли, чьими разработками активно пользуются, например Petrel или Paradigm ), которое позволяет анализировать разные типы данных и имеет удобный графический интревфейс. Несмотря на всё удобство такие виды ПО имеют и свои недостатки — например внедрение современных алгоритмов в стабильные версии занимает много времени, а возможности автоматизации расчётов, как правило, ограничены. В такой ситуации очень удобным становится использование систем компьютерной математики и языков программирования высокого уровня, которые позволяют использовать широкую алгоритмическую базу и, вместе с тем, берут на себя много рутины. По такому принципу и построена работа с сейсмическими данными в Wolfram Mathematica. Нецелесообразно писать богатый функционал интерактивной работы с данными -важнее обеспечить загрузку из общепринятого формата, применить к ним желаемые алгоритмы и выгрузить обратно во внеший формат.
Следуя предложенной схеме, загрузим оригинальные сейсмические данные и отобразим их в Wolfram Mathematica:
Get["GeologyIO`"]
seismic3DZipPath = "seismic3D.zip";
seismic3DSEGYPath = "seismic3D.sgy";
If[FileExistsQ[seismic3DZipPath], DeleteFile[seismic3DZipPath]];
If[FileExistsQ[seismic3DSEGYPath], DeleteFile[seismic3DSEGYPath]];
URLDownload["https://wolfr.am/FiQIuZuH", seismic3DZipPath];
ExtractArchive[seismic3DZipPath];
seismic3DSEGY = SEGYImport[seismic3DSEGYPath]Загруженные и импортированные таким образом данные это трассы зарегистрированные на участке размером 10 на 5 километров. В том случае если данные получены по методике трёхмерной сейсморазведки (регистрация волн ведётся не вдоль отдельных геофизических профилей, а на всей площади одновременно) становится возможным получить кубы сейсмических данных. Это трёхмерные объекты, вертикальные и горизонтальные срезы которых позволяют детально изучить геологическую среду. В расмотренном пример мы имеем дело как раз трёхмерными данными. Некоторые сведения мы можем получить из текстового заголовка, например так
StringPartition[seismic3DSEGY["textheader"], 80] // TableFormC 1 THIS IS DEMO FILE FOR GEOLOGYIO PACKAGE TEST
C 2
C 3
C 4
C 5 DATE USER NAME: WOLFRAM USER
C 6 SURVEY NAME: SOMEWHERE IN SIBERIA
C 7 FILE TYPE 3D SEISMIC VOLUME
C 8
C 9
C10 Z RANGE: FIRST 2200M LAST 2400M
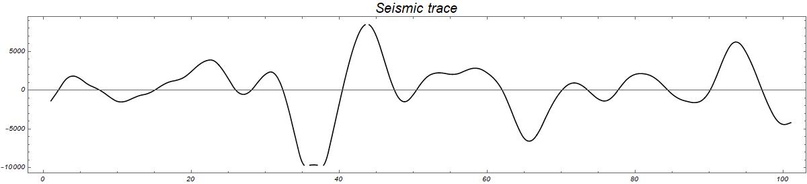
Этого набора данных нам будет достаточно, чтобы продемонстрировать основные этапы анализа данных. Трассы в файле записаны последовательно и каждая из них выглядит примерно как на следующем рисунке -это распредение амплитуд отражённых волн вдоль вертикальной оси (оси глубин).
ListLinePlot[seismic3DSEGY["traces"][[100]], InterpolationOrder -> 2,
PlotStyle -> Black, PlotLabel -> Style["Seismic trace", Black, 20],
LabelStyle -> Directive[Black, Italic], PlotRange -> All,
Frame -> True, ImageSize -> 1200, AspectRatio -> 1/5]Одна из трасс сейсмического разреза
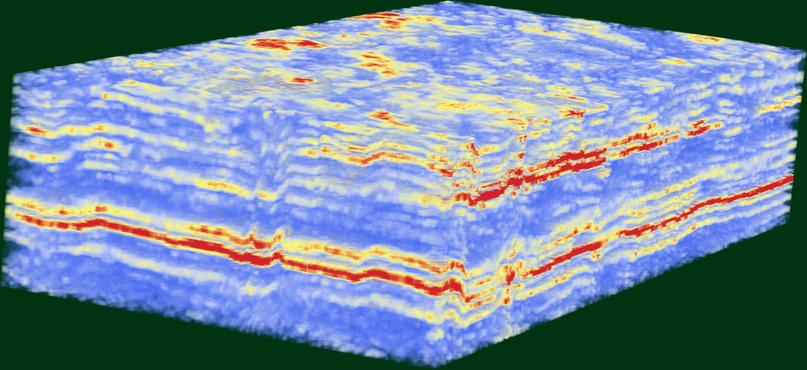
Зная то, какое количество трасс расположено в каждом направлении изученного участка можно сформировать трёхмерный массив данных и отобразить его с помощью функции Image3D[]
traces=seismic3DSEGY["traces"];
startIL=1050;EndIL=2000;stepIL=2; (*координата Х начала и конца съёмки и шаг трасс*)
startXL=1165;EndXL=1615;stepXL=2; (*координата Y начала и конца съёмки и шаг трасс*)
numIL=(EndIL-startIL)/stepIL+1; (*количество трасс по оис Х*)
numXL=(EndXL-startXL)/stepIL+1; (*количество трасс по оис Y*)
Image3D[ArrayReshape[Abs[traces/Max[Abs[traces[[All,1;;;;4]]]]],{numIL,numXL,101}],ViewPoint->{-1, 0, 0},Background->RGBColor[0,0,0]]Трёхмерное изображение куба сейсмических данных.(Вертикальная ось — глубина)
В том случае если геологические объекты, представляющие интерес, создают интенсивные сейсмические аномалии, то можно использовать инструменты визуализации с прозрачностью. «Неважные» участки записи можно сделать невидимыми, оставляя видимыми только аномалии. В Wolfram Mathematica это можно сделать с помощью Opacity[] и Raster3D[].
data = ArrayReshape[Abs[traces/Max[Abs[traces[[All,1;;;;4]]]]],{numIL,numXL,101}];
Graphics3D[{Opacity[0.1], Raster3D[data, ColorFunction->"RainbowOpacity"]},
Boxed->False, SphericalRegion->True, ImageSize->840, Background->None]Изображение куба сейсмических данных с использованием функций Opacity[] и Raster3D[]
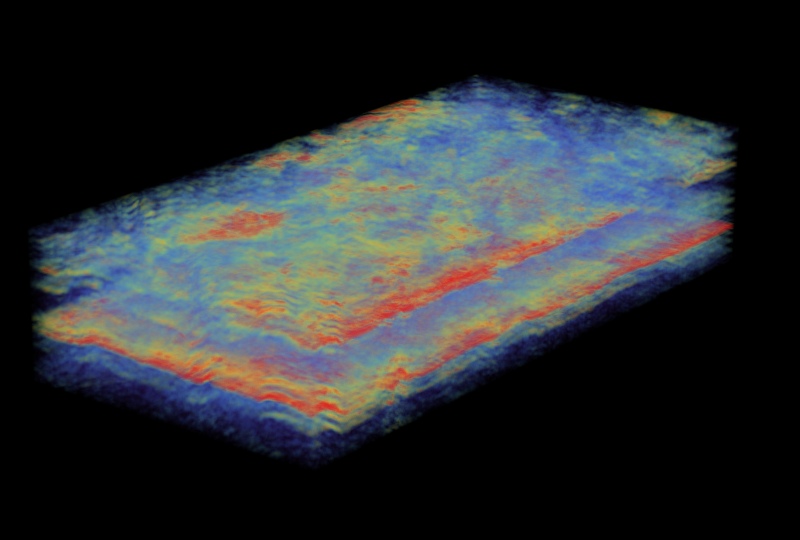
Как и на синтетическом примере, на срезах оригинального куба можно выделить некоторые геологические границы (слои) с изменчивым рельефом.
Основным инструментом спектрального анализа является преобразование Фурье. С его помощью можно оценить амплитудно-частотный спектр каждой трассы или группы трасс. Однако, после перевода данных в область частот утрачивается информация о том, на каких временах (читай на каких глубинах) меняется частота. Для того, чтобы иметь возможность локализовать изменения сигнала на временной (глубинной) оси используют оконное преобразование Фурье и вейвлет разложение. В данной статье используется вейвлет разложение. Технология вейвлет анализа стала активно применяться в сейсморазведке в 90-х годах. Преимуществом перед оконным преобразованием Фурье считается лучшая временная разрешённость.
С помощью следующего фрагмента кода можно выполнить разложение на отдельные компоненты одной из сейсмичеких трасс:
cwd=ContinuousWaveletTransform[seismicSection["traces"][[100]]]
Show[
ListLinePlot[Re[cwd[[1]]],PlotRange->All],
ListLinePlot[seismicSection["traces"][[100]],
PlotStyle->Black,PlotRange->All],ImageSize->{1500,500},AspectRatio->Full,
PlotLabel->Style["Wavelet decomposition",Black,32],
LabelStyle->Directive[Black,Italic],
PlotRange->All,
Frame->True]Разложение трассы на компоненты
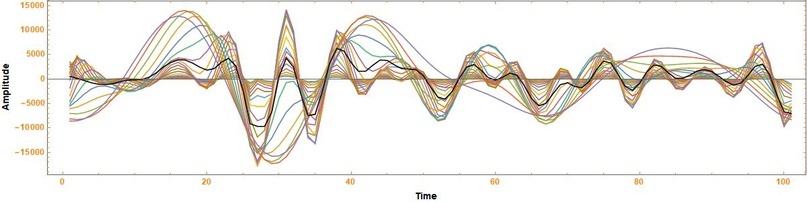
Для оценки того, как распределена энергия отражения на разных временах прихода волн используются скалограммы (аналог спектрограммы). Как правило на практике нет необходимости анализировать все компоненты. Обычно выбирают низко-, средне- и высокочастотную составляющую.
freq=(500/(#*contWD["Wavelet"]["FourierFactor"]))&/@(Thread[{Range[contWD["Octaves"]],1}]/.contWD["Scales"])//Round;
ticks=Transpose[{Range[Length[freq]],freq}];
WaveletScalogram[contWD,Frame->True,FrameTicks->{{ticks,Automatic},Automatic},FrameTicksStyle->Directive[Orange,12],
FrameLabel->{"Time","Frequency(Hz)"},LabelStyle->Directive[Black,Bold,14],
ColorFunction->"RustTones",ImageSize->Large]Скалограмма. Результат функции WaveletScalogram[]
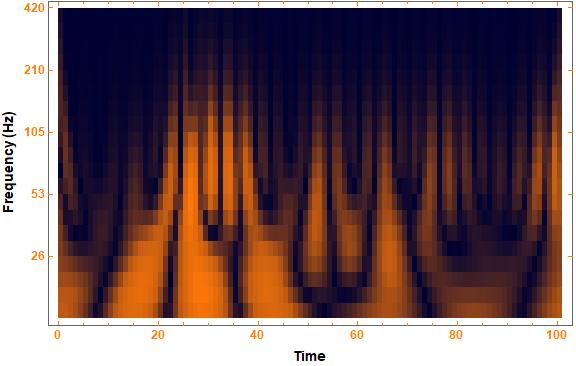
В Wolfram Language для вейвлет преобразования используется функция ContinuousWaveletTransform[]. А примение этой функции ко всему набору трасс осуществется с испольшованием функции Table[]. Здесь стоит отметить одну из сильных сторон Wolfram Mathematica возможноть использовать распрараллеливание ParallelTable[]. В приведённом примере в распаралеливании нет необходимости — объём данных не велик, но при работе с экпериментальными наборами данных содержащими сотни тысяч трасс это является необходимостью.
tracesCWD=Table[Map[Hilbert[#,0]&,Re[ContinuousWaveletTransform[traces[[i]]][[1]]][[{13,15,18}]]],{i,1,Length@traces}]; После применения функции ContinuousWaveletTransform[] появляются новые массивы данных соответствующие выбранным частотам. В приведенном выше примере это частоты: 38Гц, 33Гц, 27Гц. Выбор частот осущетвляется чаще всего на основе тестирования -получают результативные карты для разных частотных комбинаций и выбирают наиболее информативный с точки зрения геолога.
Если результатами необходимо поделиться с коллегами или предоставить их заказчику, то можно использовать функцию SEGYExport[] пакета GeologyIO
outputdata=seismic3DSEGY;
outputdata["traces",1;;-1]=tracesCWD[[All,3]];
outputdata["textheader"]="Wavelet Decomposition Result";
outputdata["binaryheader","NumberDataTraces"]=Length[tracesCWD[[All,3]]];
SEGYExport["D:\result.segy",outputdata];Имея в распоряжении три таких куба (низкочастотную, среднечастотную и высокочастотную компоненты), как правило, используют RGB смешивание для совместной визуализации данных. Каждой из компонент присваивается свой цвет — red, green, blue. В Wolfram Mathematica это можно сделать с использованием функции ColorCombine[].
В результате получаются изображения, по которым можно выполнять гелогическую интерпретацию. Меандры, которые фисируются на срезе позволяют оконтурить палеорусла, которые с большей вероятностью могут быть резервуарами и содержать запасы нефти. Поиск и анализ современных аналогов такой речной системы позволяет определить наиболее перспективные части меандр. Собственно русла характеризуются мощными слоями хорошо сортированного песчаника и являются хорошим резервуаром для нефти. Участки за пределами «шнурковых» аномалий аналогичны современным пойменным отложениям. Пойменные отложения в основном представлены глинистыми породами и бурение в эти зоны будет неэффекивным.
RGB срез куба данных. В центре (несколько левее центра) можно проследить меандрирующую реку.

RGB срез куба данных. В левой части можно проследить меандрирующую реку.

В некоторых случаях качество сейсмических данных позволяет получать существенно более чёткие изображения. Это зависит от методики полевых работ, оборудования, примяемых алгоритомв шумоподавления. В таких случаях видны не только фрагменты речных системы, но и целые протяженные палеореки.
RGB смешивание трёх компонент куба сейсмических данных (горизонтальный срез). Глубина примерно 2км.

Изображение со спутника реки Волги в районе Саратова

Заключение
В Wolfram Mathematica можно анализировать сейсмические данные и решать прикладные задачи связанные с поиском полезных ископаемых, а пакет GeologyIO позволяет сделать этот процесс более удобным. Структура сейсмических данных такова, что использование встроенных способов ускорения расчетов (ParallelTable[], ParallelDo[],...) является очень эффективным и позволяет обрабатывать большие объёмы данных. В немалой степени этому способствуют особенности хранения данных пакета GeologyIO. К слову сказать, пакет может использоваться не только в области прикладной сейсморазведки. Практически такие же типы данных используются в георадиолокации и сейсмологии.Если у вас есть предложения как улушить результат, какие алгоритмы анализа сигнала из арсенала Wolfram Mathematica применимы к таким данным или у вас имеются критические замечания -оставляйте комментарии.
Автор: Galina Mihalkina
