Сегодня мы рассмотрим графический пакет для языка Julia, который называется Luxor. Это один из тех инструментов, которые превращают процесс создания векторных изображений в решение логических задачек с сопутствующей бурей эмоций.
Осторожно! Под катом 8.5 Мб легковесных картинок и гифок изображающих психоделические яйца и четырехмерные объекты, просмотр которых может вызвать лёгкое помутнение рассудка!
Установка
https://julialang.org — скачиваем дистрибутив Джулии с официального сайта. Затем, запустив интерпретатор, вбиваем в его консоль команды:
using Pkg
Pkg.add("Colors")
Pkg.add("ColorSchemes")
Pkg.add("Luxor")что установит пакеты для расширенной работы с цветами и сам Luxor.
Возможные проблемы
Главная проблема как современного программирования в общем так и опенсорса в частности — то что одни проекты строятся поверх других, наследуя все ошибки, а то и порождая новые из-за несовместимостей. Как и многие другие пакеты Luxor использует для своей работы другие julia-пакеты, которые, в свою очередь, являются оболочками существующих решений.
Так, ImageMagick.jl не хотел загружать и сохранять файлы. Решение нашлось на странице оригинала — оказалось, он не любит кириллицу в путях.
Проблема номер два возникла с пакетом низкоуровневой графики Cairo на Windows 7. Решение упрячу здесь:
- Набираем в интерпретаторе
]add Gtk— начнет устанавливаться пакет для работы с gui и скорее всего он упадет во время построения - Далее качаем gtk+-bundle_3.6.4-20130513_win64
- В папке с пакетами Джулии во время установки накидалось всё необходимое, но во время выполнения пункта один, gtk не достроился, поэтому мы и скачали готовую версию для нашей машины — кидаем содержимое скачанного архива в директорию C:UsersUser.juliapackagesWinRPMY9QdZdepsusrx86_64-w64-mingw32sys-rootmingw (Ваш путь может отличаться)
- Запустите julia и вбейте
]build Gtkи после построенияusing Gtk, и, для пущей верности, перестроим Люксор:]build Luxor - Перезапускаем julia, и можем смело использовать всё что нужно:
using Luxor
В случае иных проблем стараемся найти свой случай
Если хочется пробовать анимацию
Пакет Luxor создает анимацию средствами ffmpeg при условии, что он присутствует на вашем компьютере. ffmpeg — это кроссплатформенная open-source библиотека для обработки видео- и аудиофайлов, очень полезная штука (есть хороший экскурс на хабре). Установим ее:
- Качаем ffmpeg с оффсайта. В моем случае это загрузка для windows
- Распаковываем и прописываем путь к ffmpeg.exe в переменную Path.
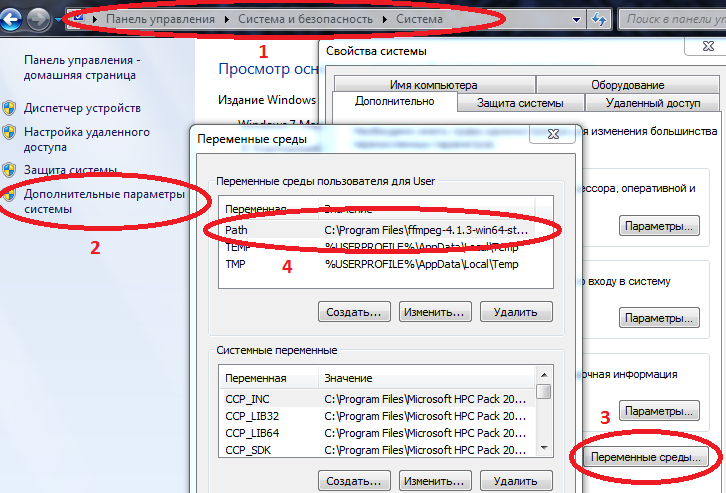
Компьютер/Свойства сиситемы/Дополнительные параметры системы/Переменные среды/Path (Создать если нет) и добавить туда путь к Вашему ffmpeg.exe
Пример C:Program Filesffmpeg-4.1.3-win64-staticbin
если в Path уже есть значения, то отделяем их точкой с запятой.
Теперь если в командную консоль (cmd) вбить ffmpeg с нужными параметрами, оно запустится и отработает, а Julia будет с ним общаться только так.
Hello world
Начнем с маленького подводного камня — при построении изображения создается графический файл и сохраняется в рабочей директории. То есть, при работе в REPL корневая папка julia будет забиваться картинками, а если рисовать в Jupyter — то картинки накапливаются рядом с блокнотом-проектом, поэтому, будет хорошей привычкой перед началом работы задавать рабочую директории в отдельно отведенном месте:
using Luxor
cd("C:\Users\User\Desktop\mycop")Создадим первый рисунок
Drawing(220, 220, "hw.png")
origin()
background("white")
sethue("black")
text("Hello world")
circle(Point(0, 0), 100, :stroke)
finish()
preview()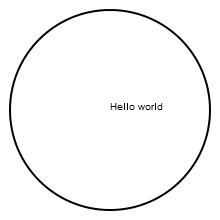
Drawing() создает рисунок, по умолчанию в формате PNG, имя файла по умолчанию 'luxor-drawing.png', размер по умолчанию 800x800, для всех форматов кроме png можно задавать нецелочисленные размеры, а также, можно использовать размеры листа бумаги ("A0", "A1", "A2", "A3", "A4"...)
finish() — завершает рисование и закрывает файл. Вы можете открыть его во внешнем приложении просмотра с помощью preview(), который при работе в Jupyter (IJulia) отобразит файл PNG или SVG в блокноте. При работе в Juno отобразит файл PNG или SVG на панели «График». В Repl же вызовется средство для работы с изображениями, которое вы задали для данного формата в своей ОС.
То же самое можно записать в короткой форме используя макросы
@png begin
text("Hello world")
circle(Point(0, 0), 100, :stroke)
endДля векторных форматов EPS, SVG, PDF всё работает аналогично.
Евклидово яйцо
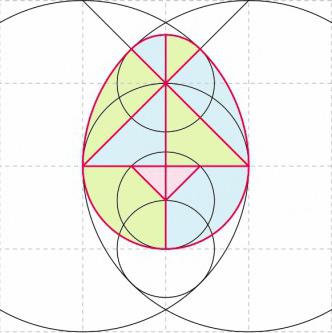
Это довольно интересный способ рисования яйца, а если соединить ключевые точки и разрезать по полученным линиям, выйдет отличный танграм
Начнем с окружности:
@png begin
radius=80
setdash("dot")
sethue("gray30")
A, B = [Point(x, 0) for x in [-radius, radius]]
line(A, B, :stroke)
circle(O, radius, :stroke)
end 200 200 "eag0" # размеры и название файла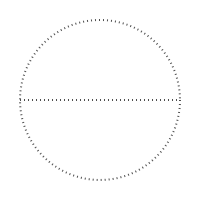
Всё предельно просто: setdash("dot") — рисуем точками, sethue("gray30") — цвет линии: чем меньше, тем темнее, чем ближе к 100 тем белее. Класс точки определен и без нас, а центр координат (0,0) можно задавать буквой O. Добавляем две окружности и подписываем точки:
@png begin
radius=80
setdash("dot")
sethue("gray30")
A, B = [Point(x, 0) for x in [-radius, radius]]
line(A, B, :stroke)
circle(O, radius, :stroke)
label("A", :NW, A)
label("O", :N, O)
label("B", :NE, B)
circle.([A, O, B], 2, :fill)
circle.([A, B], 2radius, :stroke)
end 600 400 "eag2"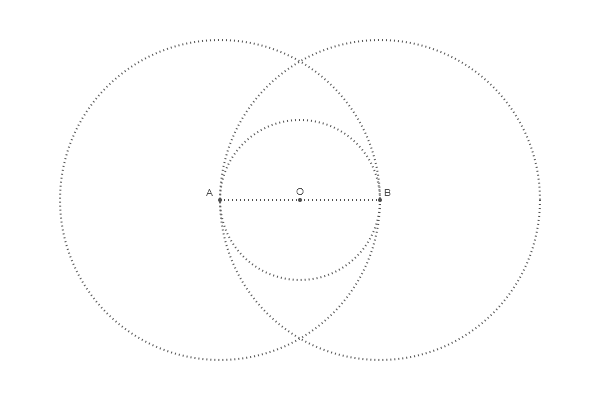
Для поиска точек пересечения есть функция, которая называется intersectionlinecircle(), которая находит точку или точки, где линия пересекает окружность. Таким образом, мы можем найти две точки, где один из кругов пересекает воображаемую вертикальную линию, проведенную через O. Из-за симметрии нам можно обработать только круг A.
@png begin
radius=80
setdash("dot")
sethue("gray30")
A, B = [Point(x, 0) for x in [-radius, radius]]
line(A, B, :stroke)
circle(O, radius, :stroke)
label("A", :NW, A)
label("O", :N, O)
label("B", :NE, B)
circle.([A, O, B], 2, :fill)
circle.([A, B], 2radius, :stroke)
# >>>>
nints, C, D =
intersectionlinecircle(Point(0, -2radius), Point(0, 2radius), A, 2radius)
if nints == 2
circle.([C, D], 2, :fill)
label.(["D", "C"], :N, [D, C])
end
end 600 400 "eag3"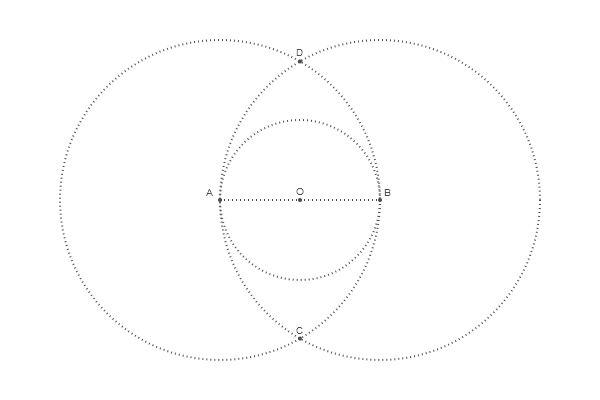
Чтоб определить центр верхней окружность найдем пересечение OD
@png begin
radius=80
setdash("dot")
sethue("gray30")
A, B = [Point(x, 0) for x in [-radius, radius]]
line(A, B, :stroke)
circle(O, radius, :stroke)
label("A", :NW, A)
label("O", :N, O)
label("B", :NE, B)
circle.([A, O, B], 2, :fill)
circle.([A, B], 2radius, :stroke)
# >>>>
nints, C1, C2 = intersectionlinecircle(O, D, O, radius)
if nints == 2
circle(C1, 3, :fill)
label("C1", :N, C1)
end
end 600 400 "eag4"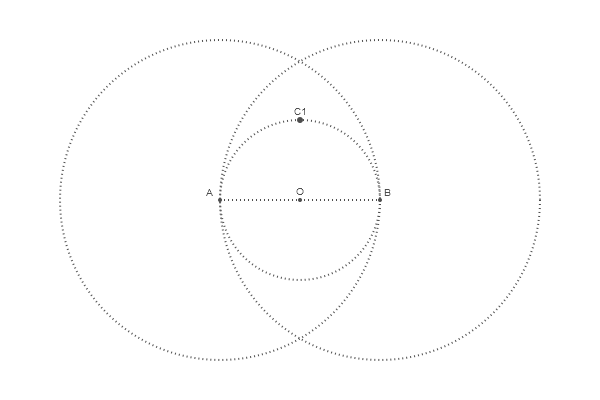
Радиус придаточной окружности определяется ограничением двумя большими окружностями:
@png begin
radius=80
setdash("dot")
sethue("gray30")
A, B = [Point(x, 0) for x in [-radius, radius]]
line(A, B, :stroke)
circle(O, radius, :stroke)
label("A", :NW, A)
label("O", :N, O)
label("B", :NE, B)
circle.([A, O, B], 2, :fill)
circle.([A, B], 2radius, :stroke)
# >>>>
nints, C1, C2 = intersectionlinecircle(O, D, O, radius)
if nints == 2
circle(C1, 3, :fill)
label("C1", :N, C1)
end
# >>>>
nints, I3, I4 = intersectionlinecircle(A, C1, A, 2radius)
nints, I1, I2 = intersectionlinecircle(B, C1, B, 2radius)
circle.([I1, I2, I3, I4], 2, :fill)
# >>>>
if distance(C1, I1) < distance(C1, I2)
ip1 = I1
else
ip1 = I2
end
if distance(C1, I3) < distance(C1, I4)
ip2 = I3
else
ip2 = I4
end
label("ip1", :N, ip1)
label("ip2", :N, ip2)
circle(C1, distance(C1, ip1), :stroke)
end 600 400 "eag5"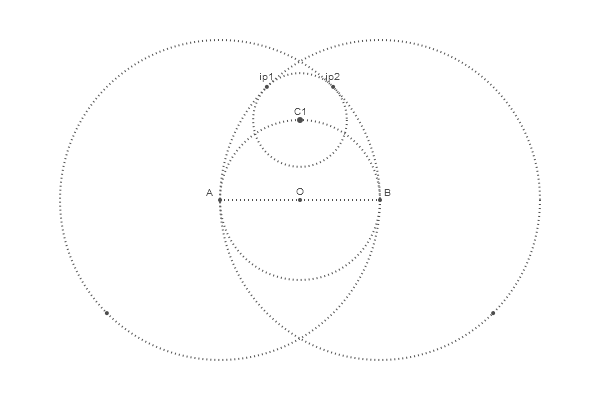
Яйцо готово! Осталось его собрать из четырех дуг, задаваемых функцией arc2r() и залить площадь:
@png begin
radius=80
setdash("dot")
sethue("gray30")
A, B = [Point(x, 0) for x in [-radius, radius]]
line(A, B, :stroke)
circle(O, radius, :stroke)
label("A", :NW, A)
label("O", :N, O)
label("B", :NE, B)
circle.([A, O, B], 2, :fill)
circle.([A, B], 2radius, :stroke)
# >>>>
nints, C1, C2 = intersectionlinecircle(O, D, O, radius)
if nints == 2
circle(C1, 3, :fill)
label("C1", :N, C1)
end
# >>>>
nints, I3, I4 = intersectionlinecircle(A, C1, A, 2radius)
nints, I1, I2 = intersectionlinecircle(B, C1, B, 2radius)
circle.([I1, I2, I3, I4], 2, :fill)
# >>>>
if distance(C1, I1) < distance(C1, I2)
ip1 = I1
else
ip1 = I2
end
if distance(C1, I3) < distance(C1, I4)
ip2 = I3
else
ip2 = I4
end
label("ip1", :N, ip1)
label("ip2", :N, ip2)
circle(C1, distance(C1, ip1), :stroke)
# >>>>
setline(5)
setdash("solid")
arc2r(B, A, ip1, :path) # centered at B, from A to ip1
arc2r(C1, ip1, ip2, :path)
arc2r(A, ip2, B, :path)
arc2r(O, B, A, :path)
strokepreserve()
setopacity(0.8)
sethue("ivory")
fillpath()
end 600 400 "eag6"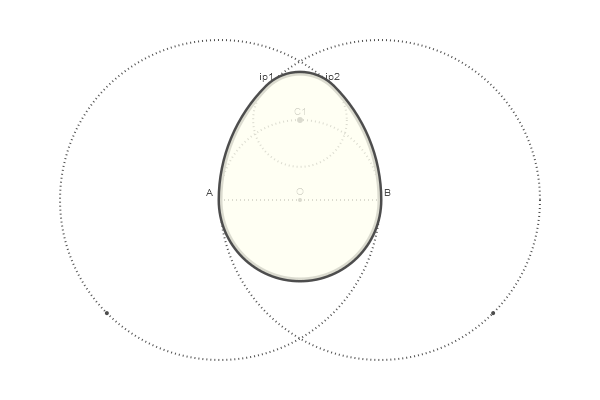
А теперь, чтоб как следует побаловаться занесем свои наработки в
function egg(radius, action=:none)
A, B = [Point(x, 0) for x in [-radius, radius]]
nints, C, D =
intersectionlinecircle(Point(0, -2radius), Point(0, 2radius), A, 2radius)
flag, C1 = intersectionlinecircle(C, D, O, radius)
nints, I3, I4 = intersectionlinecircle(A, C1, A, 2radius)
nints, I1, I2 = intersectionlinecircle(B, C1, B, 2radius)
if distance(C1, I1) < distance(C1, I2)
ip1 = I1
else
ip1 = I2
end
if distance(C1, I3) < distance(C1, I4)
ip2 = I3
else
ip2 = I4
end
newpath()
arc2r(B, A, ip1, :path)
arc2r(C1, ip1, ip2, :path)
arc2r(A, ip2, B, :path)
arc2r(O, B, A, :path)
closepath()
do_action(action)
endИспользуем рандомные цвета, рисование слоями и различные начальные условия:
@png begin
setopacity(0.7)
for θ in range(0, step=π/6, length=12)
@layer begin
rotate(θ)
translate(100, 50)
# translate(0, -150)
#rulers()
egg(50, :path)
setline(10)
randomhue()
fillpreserve()
randomhue()
strokepath()
end
end
end 400 400 "eags2"

Помимо обводки и заливки, вы можете использовать контур в качестве области отсечения (обрезать другое изображение в форму яйца) или в качестве основы для различных конструкторов. Функция egg() создает контур и позволяет применить к нему действие. Также возможно преобразовать наше творение в многоугольник (массив точек). Следующий код преобразует контур яйца в многоугольник, а затем перемещает каждую другую точку многоугольника на полпути к центроиду.
@png begin
egg(160, :path)
pgon = first(pathtopoly())
pc = polycentroid(pgon)
circle(pc, 5, :fill)
for pt in 1:2:length(pgon)
pgon[pt] = between(pc, pgon[pt], 0.5)
end
poly(pgon, :stroke)
end 350 500 "polyeag"
Неравномерный внешний вид внутренних точек здесь выходит как результат настроек соединения линий по умолчанию. Поэкспериментируйте с setlinejoin("round"), чтобы увидеть, не изменит ли это геометрию. Ну а теперь попробуем offsetpoly() создающую многоугольный контур вне или внутри существующего многоугольника..
@png begin
egg(80, :path)
pgon = first(pathtopoly())
pc = polycentroid(pgon)
for pt in 1:2:length(pgon)
pgon[pt] = between(pc, pgon[pt], 0.9)
end
for i in 30:-3:-8
randomhue()
op = offsetpoly(pgon, i)
poly(op, :stroke, close=true)
end
end 350 500 "polyeags"
Небольшие изменения в регулярности точек, создаваемых преобразованием пути в многоугольник, и разное количество выборок, которые оно делало, постоянно усиливаются в последовательных контурах.
Анимация
Для начала зададим функции реализующие фон и отрисовку яйца в зависимости от номера кадра:
using Colors
demo = Movie(400, 400, "test")
function backdrop(scene, framenumber)
background("black")
end
function frame(scene, framenumber)
setopacity(0.7)
θ = framenumber * π/6
@layer begin
rotate(θ)
translate(100, 50)
egg(50, :path)
setline(10)
randomhue()
fillpreserve()
randomhue()
strokepath()
end
endАнимация реализуется простым набором команд:
animate(demo, [
Scene(demo, backdrop, 0:12),
Scene(demo, frame, 0:12,
easingfunction=easeinoutcubic,
optarg="made with Julia")
],
framerate=10,
tempdirectory="C:\Users\User\Desktop\mycop",
creategif=true)Что на самом деле вызывает наш ffmpeg
run(`ffmpeg -f image2 -i $(tempdirectory)/%10d.png -vf palettegen
-y $(seq.stitle)-palette.png`)
run(`ffmpeg -framerate 30 -f image2 -i $(tempdirectory)/%10d.png
-i $(seq.stitle)-palette.png -lavfi paletteuse -y /tmp/$(seq.stitle).gif`)То есть, создается серия изображений, а потом из этих фрэймов собирается гифка:

Пентахор
Он же пятиячейник — правильный четырехмерный симплекс. Чтобы рисовать и манипулировать на двумерных картинках 4-мерные объекты, для начала определим
struct Point4D <: AbstractArray{Float64, 1}
x::Float64
y::Float64
z::Float64
w::Float64
end
Point4D(a::Array{Float64, 1}) = Point4D(a...)
Base.size(pt::Point4D) = (4, )
Base.getindex(pt::Point4D, i) = [pt.x, pt.y, pt.z, pt.w][i]
struct Point3D <: AbstractArray{Float64, 1}
x::Float64
y::Float64
z::Float64
end
Base.size(pt::Point3D) = (3, )Вместо того, чтобы определять множество операций вручную, мы можем задать нашу структуру как подтип AbstractArray (Подробней про классы как интерфейсы)
Основная задача, которую мы должны решить, — это как преобразовать 4D точку в 2D точку. Давайте начнем с более простой задачи: как преобразовать 3D-точку в 2D-точку, т.е. как мы можем нарисовать 3D-фигуру на плоской поверхности? Рассмотрим простой куб. Передняя и задняя поверхности могут иметь одинаковые координаты X и Y и изменяться только по своим значениям Z.
@png begin
fontface("Menlo")
fontsize(8)
setblend(blend(
boxtopcenter(BoundingBox()),
boxmiddlecenter(BoundingBox()),
"skyblue",
"white"))
box(boxtopleft(BoundingBox()),
boxmiddleright(BoundingBox()), :fill)
setblend(blend(
boxmiddlecenter(BoundingBox()),
boxbottomcenter(BoundingBox()),
"grey95",
"grey45"
))
box(boxmiddleleft(BoundingBox()),
boxbottomright(BoundingBox()), :fill)
sethue("black")
setline(2)
bx1 = box(O, 250, 250, vertices=true)
poly(bx1, :stroke, close=true)
label.(["-1 1 1", "-1 -1 1", "1 -1 1", "1 1 1"],
slope.(O, bx1), bx1)
setline(1)
bx2 = box(O, 150, 150, vertices=true)
poly(bx2, :stroke, close=true)
label.(["-1 1 0", "-1 -1 0", "1 -1 0", "1 1 0"],
slope.(O, bx2), bx2, offset=-45)
map((x, y) -> line(x, y, :stroke), bx1, bx2)
end 400 400 "cube.png"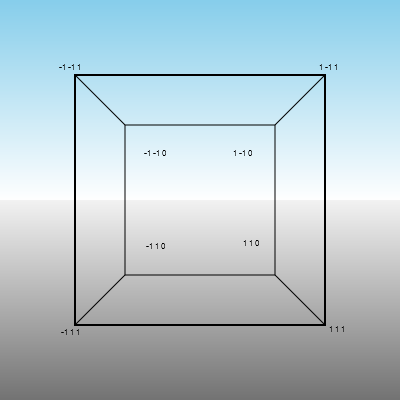
Поэтому идея состоит в том, чтобы спроецировать куб из 3D в 2D, сохранив первые два значения и умножив или изменив их на третье значение. Проверим
const K = 4.0
function convert(Point, pt3::Point3D)
k = 1/(K - pt3.z)
return Point(pt3.x * k, pt3.y * k)
end
@png begin
cube = Point3D[
Point3D(-1, -1, 1),
Point3D(-1, 1, 1),
Point3D( 1, -1, 1),
Point3D( 1, 1, 1),
Point3D(-1, -1, -1),
Point3D(-1, 1, -1),
Point3D( 1, -1, -1),
Point3D( 1, 1, -1),
]
circle.(convert.(Point, cube) * 300, 5, :fill)
end 220 220 "points"
Используя тот же принцип, давайте создадим метод для преобразования 4D-точки и функцию, которая берет список четырехмерных точек и дважды отображает их в список двухмерных точек, подходящих для рисования.
function convert(Point3D, pt4::Point4D)
k = 1/(K - pt4.w)
return Point3D(pt4.x * k, pt4.y * k, pt4.z * k)
end
function flatten(shape4)
return map(pt3 -> convert(Point, pt3), map(pt4 -> convert(Point3D, pt4), shape4))
endДалее задаем вершины и грани и проверяем, как оно работает в цвете
const n = -1/√5
const pentachoron = [Point4D(vertex...) for vertex in [
[ 1.0, 1.0, 1.0, n],
[ 1.0, -1.0, -1.0, n],
[-1.0, 1.0, -1.0, n],
[-1.0, -1.0, 1.0, n],
[ 0.0, 0.0, 0.0, n + √5]]];
const pentachoronfaces = [
[1, 2, 3],
[1, 2, 4],
[1, 2, 5],
[1, 3, 4],
[1, 3, 5],
[1, 4, 5],
[2, 3, 4],
[2, 3, 5],
[2, 4, 5],
[3, 4, 5]];
@png begin
setopacity(0.2)
pentachoron2D = flatten(pentachoron)
for (n, face) in enumerate(pentachoronfaces)
randomhue()
poly(1500 * pentachoron2D[face], :fillpreserve, close=true)
sethue("black")
strokepath()
end
end 300 250 "5ceil"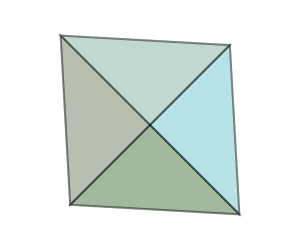
Каждый уважающий себя разработчик игр должен знать Математические основы машинной графики. Если же вы никогда не пытались сжимать, вращать, отражать чайники в OpenGL — не пугайтесь, всё довольно просто. Чтоб отразить точку относительно прямой, или чтобы повернуть плоскость вокруг определенной оси, нужно домножить координаты на специальную матрицу. Собственно далее мы и определим нужные нам матрицы преобразований:
function XY(θ)
[cos(θ) -sin(θ) 0 0;
sin(θ) cos(θ) 0 0;
0 0 1 0;
0 0 0 1]
end
function XW(θ)
[cos(θ) 0 0 -sin(θ);
0 1 0 0;
0 0 1 0;
sin(θ) 0 0 cos(θ)]
end
function XZ(θ)
[cos(θ) 0 -sin(θ) 0;
0 1 0 0;
sin(θ) 0 cos(θ) 0;
0 0 0 1]
end
function YZ(θ)
[1 0 0 0;
0 cos(θ) -sin(θ) 0;
0 sin(θ) cos(θ) 0;
0 0 0 1]
end
function YW(θ)
[1 0 0 0;
0 cos(θ) 0 -sin(θ);
0 0 1 0;
0 sin(θ) 0 cos(θ)]
end
function ZW(θ)
[1 0 0 0;
0 1 0 0;
0 0 cos(θ) -sin(θ);
0 0 sin(θ) cos(θ)];
end
function rotate4(A, matrixfunction)
return map(A) do pt4
Point4D(matrixfunction * pt4)
end
endОбычно вы поворачиваете точки на плоскости относительно одномерного объекта. 3D-точки — вокруг 2D-линии (часто это одна из осей XYZ). Таким образом, логично что 4D точки поворачиваются относительно 3D-плоскости. Мы определили матрицы, которые выполняют четырехмерное вращение относительно плоскости, определяемой двумя осями X, Y, Z и W. Плоскость XY обычно является плоскостью поверхности рисования. Если вы воспринимаете плоскость XY как экран компьютера то, плоскость XZ параллельна вашему столу или полу, а плоскость YZ — это стены рядом с вашим столом справа или слева. А как же XW, YW и ZW? Это тайна четырехмерных фигур: мы не можем видеть эти плоскости, мы можем только представить их существование, наблюдая, как формы движутся сквозь них и вокруг них.
Теперь задаем функции для фрэймов и сшиваем анимацию:
using ColorSchemes
function frame(scene, framenumber, scalefactor=1000)
background("white") # antiquewhite
setlinejoin("bevel")
setline(1.0)
sethue("black")
eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop)
pentachoron′ = rotate4(pentachoron, XZ(eased_n * 2π))
pentachoron2D = flatten(pentachoron′)
setopacity(0.2)
for (n, face) in enumerate(pentachoronfaces)
sethue(get(ColorSchemes.diverging_rainbow_bgymr_45_85_c67_n256,
n/length(pentachoronfaces)))
poly(scalefactor * pentachoron2D[face], :fillpreserve, close=true)
sethue("black")
strokepath()
end
end
function makemovie(w, h, fname;
scalefactor=1000)
movie1 = Movie(w, h, "4D movie")
animate(movie1,
Scene(movie1, (s, f) -> frame(s, f, scalefactor),
1:300,
easingfunction=easeinoutsine),
#framerate=10,
tempdirectory="C:\Users\User\Desktop\mycop",
creategif=true,
pathname="C:\Users\User\Desktop\mycop\$(fname)")
end
makemovie(320, 320, "pentachoron-xz.gif", scalefactor=2000)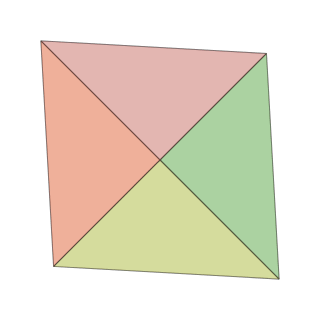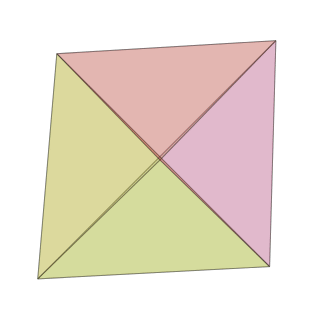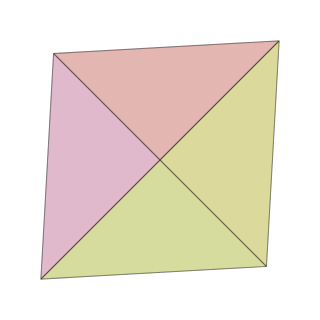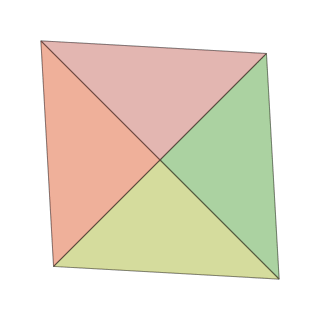
Ну, и еще ракурс:
function frame(scene, framenumber, scalefactor=1000)
background("antiquewhite")
setlinejoin("bevel")
setline(1.0)
setopacity(0.2)
eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop)
pentachoron2D = flatten(
rotate4(
pentachoron,
XZ(eased_n * 2π) *
YW(eased_n * 2π)))
for (n, face) in enumerate(pentachoronfaces)
sethue(get(ColorSchemes.diverging_rainbow_bgymr_45_85_c67_n256,
n/length(pentachoronfaces)))
poly(scalefactor * pentachoron2D[face], :fillpreserve, close=true)
sethue("black")
strokepath()
end
end
makemovie(500, 500, "pentachoron-xz-yw.gif", scalefactor=2000)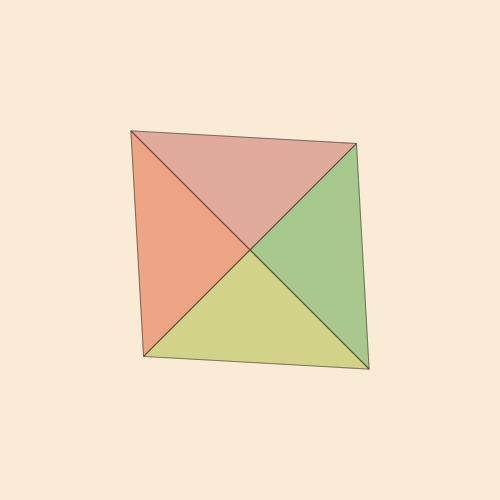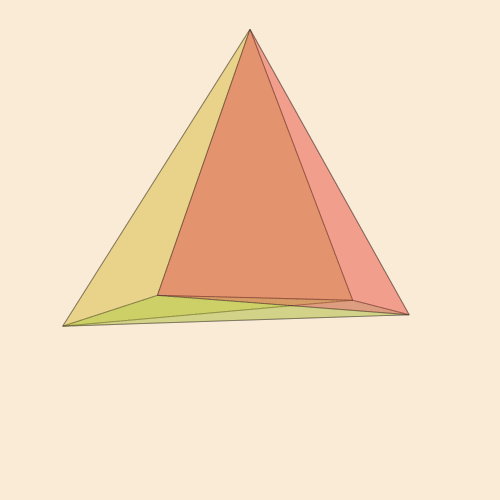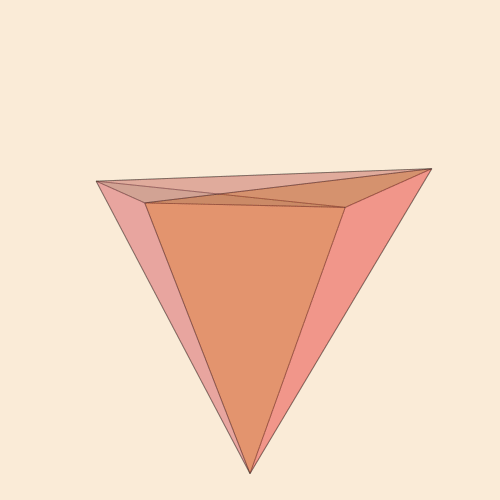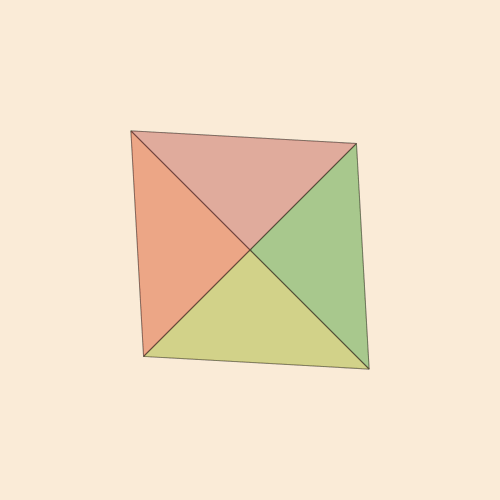
Совершено естественно желание реализовать более популярный четырехмерный объект — Тессеракт
const tesseract = [Point4D(vertex...) for vertex in [
[-1, -1, -1, 1],
[ 1, -1, -1, 1],
[ 1, 1, -1, 1],
[-1, 1, -1, 1],
[-1, -1, 1, 1],
[ 1, -1, 1, 1],
[ 1, 1, 1, 1],
[-1, 1, 1, 1],
[-1, -1, -1, -1],
[ 1, -1, -1, -1],
[ 1, 1, -1, -1],
[-1, 1, -1, -1],
[-1, -1, 1, -1],
[ 1, -1, 1, -1],
[ 1, 1, 1, -1],
[-1, 1, 1, -1]]]
const tesseractfaces = [
[1, 2, 3, 4],
[1, 2, 10, 9],
[1, 4, 8, 5],
[1, 5, 6, 2],
[1, 9, 12, 4],
[2, 3, 11, 10],
[2, 3, 7, 6],
[3, 4, 8, 7],
[5, 6, 14, 13],
[5, 6, 7, 8],
[5, 8, 16, 13],
[6, 7, 15, 14],
[7, 8, 16, 15],
[9, 10, 11, 12],
[9, 10, 14, 13],
[9, 13, 16, 12],
[10, 11, 15, 14],
[13, 14, 15, 16]];function frame(scene, framenumber, scalefactor=1000)
background("black")
setlinejoin("bevel")
setline(10.0)
setopacity(0.7)
eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop)
tesseract2D = flatten(
rotate4(
tesseract,
XZ(eased_n * 2π) *
YW(eased_n * 2π)))
for (n, face) in enumerate(tesseractfaces)
sethue([Luxor.lighter_blue, Luxor.lighter_green,
Luxor.lighter_purple, Luxor.lighter_red][mod1(n, 4)]...)
poly(scalefactor * tesseract2D[face], :fillpreserve, close=true)
sethue([Luxor.darker_blue, Luxor.darker_green,
Luxor.darker_purple, Luxor.darker_red][mod1(n, 4)]...)
strokepath()
end
end
makemovie(500, 500, "tesseract-xz-yw.gif", scalefactor=1000)
Домашнее задание: автоматизируйте создание массивов координат и номеров вершин (перестановки с повторениями и без повторений соответственно). Также мы использовали не все транслирующие матрицы; каждый новый ракурс вызывает новый "Ух-тыж!", но я решил не перегружать страницу. Ну и можно поэкспериментировать с большим количеством граней и измерений.
Ссылки
- Luxor — страница на гитхабе
- Luxor docs — руководство с примерами
- Cairo — низкоуровневая графическая библиотека; используется Люксором как окружение
- Блог автора библиотеки — там много всякой крутотени и более расширенных примеров, включая четырехмерные фигуры.
Автор: Yermack
