Джулия в лабиринте

в 6:07, , рубрики: astar, Julia, алгоритм Прима, Лабиринты, ненормальное программирование, олимпиадные задачи, поиск в глубину, Программирование, Спортивное программирование

Джулия в лабиринте - 1

Разбирая одну олимпиадную задачу мы отправимся по петляющим коридорам генерации лабиринтов и их прохождения, а также увидим, что на языке Julia простота реализаций алгоритмов граничит с их псевдокодом.

Задача

Лабиринт представляет собой клетчатый квадрат 10 на 10, в некоторых клетках стоят препятствия, а в одной клетке находится выход. Робот находится в таком лабиринте и может выполнять 4 команды: сдвинуться на одну клетку вниз, вверх, вправо или влево. Если робот пытается выйти за границы лабиринта или перейти в клетку с препятствием, то он остается на месте. Если робот попадает в выход, то он выходит из лабиринта и дальнейшие команды игнорирует. Напишите программу для робота, исполняя которую робот в любом случае доберется до выхода вне зависимости от клетки, в которой он находился вначале. Программа должна состоять из не более чем 1000 команд.

Джулия в лабиринте - 2

Формат ввода

Ввода нет. Нужно написать программу для одного конкретного указанного в условии
лабиринта.
Версия лабиринта, которую можно скопировать. 0 — свободная клетка, 1 — препятствие, x —
выход.

0011010011
0100001000
0110x00000
0010000100
0000111000
0000100100
0000010010
0100101010
0011001010
1000011000

Формат вывода

Одна строка, состоящая из символов U,D,R,L длины не более 1000

Подготовка

Тем, кто не работал с графикой в Julia нужно докачать пакеты

using Pkg
Pkg.add("Plots")
Pkg.add("Colors")
Pkg.add("Images")
Pkg.build("Images") # если сам не отбилдится

Удобней всего работать в Jupyter, так как картинки будут отображаться непосредственно по ходу работы. Здесь можно найти про установку, а также введение и задания для начинающих.

В условии нашей задачи есть версия лабиринта для копирования

S0 = "0011010011
0100001000
0110x00000
0010000100
0000111000
0000100100
0000010010
0100101010
0011001010
1000011000"

Чтоб рисовать лабиринт, нужно составить матрицу. Так как не хочется расставлять пробелы вручную, поработаем со строкой:

S1 = prod(s-> s*' ', '['*S0*']')
# prod(fun, arr) перемножает элементы массива arr 
# прогоняя их через функцию fun
# в julia операция * склеивает строки

"[ 0 0 1 1 0 1 0 0 1 1 n 0 1 0 0 0 0 1 0 0 0 n 0 1 1 0 x 0 0 0 0 0 n 0 0 1 0 0 0 0 1 0 0 n 0 0 0 0 1 1 1 0 0 0 n 0 0 0 0 1 0 0 1 0 0 n 0 0 0 0 0 1 0 0 1 0 n 0 1 0 0 1 0 1 0 1 0 n 0 0 1 1 0 0 1 0 1 0 n 1 0 0 0 0 1 1 0 0 0 ] "

Заменив несуразную букву х на цифру и отпарсив строку, получим целочисленную матрицу задающую наш лабиринт. Затем, для большего удобства, поменяем единички на нули, а нули на единицы, и обнесем лабиринт стеной:

S2 = replace(S1, 'x'=>'9')
M0 = S2 |> Meta.parse |> eval

m,n = size(M0)
M1 = replace(M0, 1=>0, 0=>1)
M = zeros(Int64,m+2,n+2)
for i in 2:m+1, j in 2:n+1
    M[i,j] = M1[i-1,j-1]
end
M # Maze map matrix 

12×12 Array{Int64,2}:
 0  0  0  0  0  0  0  0  0  0  0  0
 0  1  1  0  0  1  0  1  1  0  0  0
 0  1  0  1  1  1  1  0  1  1  1  0
 0  1  0  0  1  9  1  1  1  1  1  0
 0  1  1  0  1  1  1  1  0  1  1  0
 0  1  1  1  1  0  0  0  1  1  1  0
 0  1  1  1  1  0  1  1  0  1  1  0
 0  1  1  1  1  1  0  1  1  0  1  0
 0  1  0  1  1  0  1  0  1  0  1  0
 0  1  1  0  0  1  1  0  1  0  1  0
 0  0  1  1  1  1  0  0  1  1  1  0
 0  0  0  0  0  0  0  0  0  0  0  0

В матрице

length(M)
144

клетки, и из них 

sum(M)-9 
70

по которым можно ходить, то есть — потенциальных стартовых позиций. Изобразить результат можно построив двумерную гистограмму

using Plots
heatmap(M, yaxis = :flip) # flip - инвертирует ось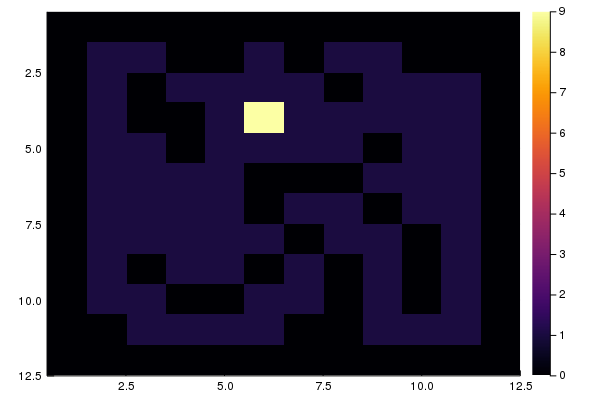

Джулия в лабиринте - 3

Проверка решения

Прежде всего, нужно отработать процедуры, которые будут проверять правильность предложенного решения. Зададим составной тип Point, чтобы пользоваться терминологией точек и координат:

mutable struct Point
    x::Int64 # vertical
    y::Int64 # horisont
    Point(x, y) = new(x, y)
end

А теперь нужно научиться переводить последовательность команд понятных для робота в код.

Мысль довольно проста: есть стартовая координата, приходит строка с алгоритмом, говорящим как ходить. Берем по одной буковке и смотрим, на какую из соседних клеток наступать. К текущей координате прибавляем значение которое хранится в этой клетке. То есть, если там ноль (стена), мы никуда не сдвинулись, иначе — сделали шажок в требуемом направлении.

Можно воспользовавшись мощью метапрограммирования заменить поступающую последовательность направлений на громоздкий однообразный код и выполнить его

S = "RRLDUURULDDRDDRRRUUU"

S1 = replace(S , "R"=>"c.y+=M[c.x, c.y+1];")
S1 = replace(S1, "L"=>"c.y-=M[c.x, c.y-1];")
S1 = replace(S1, "U"=>"c.x+=M[c.x+1, c.y];")
S1 = replace(S1, "D"=>"c.x-=M[c.x-1, c.y];")
# с - start point
Sp = eval( Meta.parse(S1) )

Но этот способ несет за собой ряд неудобств, поэтому воспользуемся классическими условными операторами. Кстати, в том что выход обозначен цифрой 9 есть небольшая хитрость: чтоб не проверять каждую клетку, а не выход ли это, мы инициируем передвижение прибавляя значение хранящееся в конкретной клетке. Когда робот наступает на выход к его координате присуммируется заведомо большое число, такое что робот вылетает за границы массива, что можно отловить как ошибку с помощью блока:

try
    # если здесь произошла ошибка
catch
    # то выполняются действия из этого поля
end

Таким образом реализуем функцию, которая будет проверять, достигает ли робот выхода стартуя из точки c выполняя команды из строки str:

function isexit(str, c)
    scatter!([c.y],[c.x])
    try
        for s in str
            if s == 'R'
                c.y+=M[c.x, c.y+1];

            elseif s == 'L' 
                c.y-=M[c.x, c.y-1];

            elseif s == 'U'
                c.x+=M[c.x+1, c.y];

            elseif s == 'D'
                c.x-=M[c.x-1, c.y];

            else
                 println("Error! Use only R, L, U, D")
            end

        end
    catch
        return true
    end
    return false
end

Соберем функцию, которая переберет все стартовые позиции

function test(Str)
    k = 0
    for i in 2:m+1, j in 2:n+1
        if M[i,j] == 1
            c = Point(i, j)
            a = isexit(S,c)
            if a
                k +=1
                #println(a)
            end
        end
    end
    println(k, " test completed from ", sum(M)-9)
end

Проверим команды:

S = "RRRLDUUURRRUUURRRRLLLRRUULDDDDRRRRDDDRRRUUU"
heatmap(M, yaxis = :flip)
test(S)
# 10 test completed from 70
plot!(legend = false)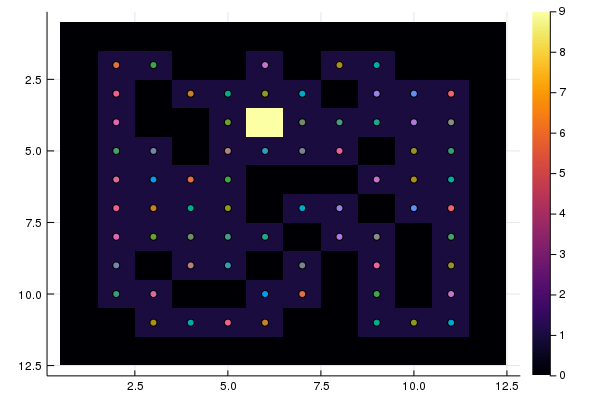

Джулия в лабиринте - 4
Опробованы все стартовые точки, и только 10 привели к выходу. Нужно построить маршруты от каждой точки до выхода.

Прежде чем погрузиться в генерацию и прохождение лабиринтов, сохраним наши результаты. Воспользуемся пакетом Images.jl предоставляющим множество возможностей в области обработки изображений (наглядный пример). Одним из его вспомогательных инструментов является пакет Colors.jl расширяющий возможности Джулии работой с цветами.

using Images
clrs(x) = x==9 ? RGB(1.,0.5,0) : RGB(x,x,x)
maze = clrs.(M)
# maze = Gray.(maze)
# save("D:/dat/maze12x12.png", maze)

Джулия в лабиринте - 5

Поиск в глубину

Реализована идея из статьи на хабре.
Идея проста: создаем сетку из стен

M = 10
N = 10
A = [ i&j&1 for i in 0:N, j in 0:M ] # isodd(i) & isodd(j) & 1
Gray.(A) # from Images.jl

Джулия в лабиринте - 6

затем, петляя пробиваем маршрут и ответвления. Зададим функцию находящую соседние непосещенные области (будем обозначать их, скажем, двойкой) и возвращающую одного из этих соседей (если непосещенных соседей нет — возвращает флаг-точку):

function neighbours2(A,p, n, m)
    nbrs = [Point(p.x, p.y+2), # up
            Point(p.x, p.y-2), # down
            Point(p.x-2, p.y), # left
            Point(p.x+2, p.y)] # right
    goal = []
    for a in nbrs
        if 0<a.x<=n && 0<a.y<=m && A[a.x,a.y]==2
            push!(goal, a)
        end
    end
    length(goal) != 0 ? rand(goal) : Point(-1,-1)
end

Стены будем разбивать так:

function breakwall(A, newp,oldp)
    # координата стены:
    x = (newp.x + oldp.x) >> 1 # побитовый сдвиг
    y = (newp.y + oldp.y) >> 1
    A[x,y] = 1
end

Алгоритм

  1. Сделайте начальную клетку текущей и отметьте ее как посещенную.
  2. Пока есть непосещенные клетки
      1. Если текущая клетка имеет непосещенных «соседей»
        1. Протолкните текущую клетку в стек
        2. Выберите случайную клетку из соседних
        3. Уберите стенку между текущей клеткой и выбранной
        4. Сделайте выбранную клетку текущей и отметьте ее как посещенную.
      2. Иначе если стек не пуст
        1. Выдерните клетку из стека
        2. Сделайте ее текущей
      3. Иначе
        1. Выберите случайную непосещенную клетку, сделайте ее текущей и отметьте как посещенную.

Код программы

function amazeng(n, m)

    M = [ 2(i&j&1) for i in 0:n, j in 0:m ];
    p = Point(2,2) # стартовая точа
    lifo = [] # пустой массив
    push!(lifo, p)
    #i = 0
    while length(lifo) != 0 # пока не опустеет стек
        M[p.x,p.y] = 1 # отметим белым посещенную клетку
        np = neighbours2(M, p, n, m) # new point
        # если нет соседей - идём обратно
        if np.x == np.y == -1
            p = pop!(lifo)
        else
            push!(lifo, p)
            breakwall(M, np, p)
            p = np
            #i+=1
            #maze = Gray.(M/2)
            #save("D:/dat/maze$i.png", maze)
        end
    end

    M[1,2] = 1 # вход
    M[n,m+1] = 1 # выход

    Gray.(M)
end

lbrnt = amazeng(36, 48)
# save("D:/dat/maze111.png", lbrnt)

Джулия в лабиринте - 7

Джулия в лабиринте - 8

Алгоритм поиска пути бэктрекингом:

  1. Сделайте начальную клетку текущей и отметьте ее как посещенную.
  2. Пока не найден выход
      1. Если текущая клетка имеет непосещенных «соседей»
        1. Протолкните текущую клетку в стек
        2. Выберите случайную клетку из соседних
        3. Сделайте выбранную клетку текущей и отметьте ее как посещенную.
      2. Иначе если стек не пуст
        1. Выдерните клетку из стека
        2. Сделайте ее текущей
      3. Иначе выхода нет

Соседей ищем наоборот и в радиусе одной клетки, а не через одну:

function neighbours1(A, p, n, m)
    nbrs = [Point(p.x, p.y+1), # up
            Point(p.x, p.y-1), # down
            Point(p.x-1, p.y), # left
            Point(p.x+1, p.y)] # right
    goal = []
    for a in nbrs
        if 0<a.x<=n && 0<a.y<=m && A[a.x,a.y]==1
            push!(goal, a)
        end
    end
    length(goal) != 0 ? rand(goal) : Point(0,0)
end

Зададим алгоритм прохождения лабиринта с отрисовкой маршрута и неудачных попыток

function amazeng(img, start, exit)
    M = Float64.(channelview(img))
    n, m = size(M)
    p = start
    M[exit.x,exit.y] = 1

    lifo = []
    push!(lifo, p)

    while p.x != exit.x || p.y != exit.y

        M[p.x,p.y] = 0.4
        np = neighbours1(M, p, n, m)
        if np.x == np.y == 0
            M[p.x,p.y] = 0.75
            p = pop!(lifo)
# числа  - оттенки серого, чтоб выделить маршрут
# можно поставить функции задающие цвета
        else
            push!(lifo, p)
            p = np
        end
    end

    Gray.(M)
end

Как некоторые заметили, функция называется также, как и та, что алгоритмы генерирует (Множественная диспетчеризация). При вызове ее с двумя числами, отработает метод конструирования лабиринта, если же вызвать, задав в качестве аргумента изображение и две точки (координаты входа и выхода), то на выходе получим изображение с пройденным лабиринтом

img0 = load("D:/dat/maze111.png")
amazeng(img0)

Джулия в лабиринте - 9

Отпробуем на нашем лабиринте:

img0 = load("D:/dat/maze12x12.png")
n, m = size(img0)
amazeng(img0, Point(11,9), Point(4,6) )

Джулия в лабиринте - 10

Даже если модифицировать функцию, чтоб запоминался маршрут, всё равно из-за открытых пространств алгоритм показывает себя неэффективным. Зато лабиринты выходят отличные.

Рандомизированный алгоритм Прима

Уж как начнешь рисовать лабиринты, так и не остановиться. Выполним еще один интересный алгоритм:

  • Начать с сетки, полной стен.
  • Выберите ячейку, отметьте ее как часть лабиринта. Добавьте стены ячейки в список стен.
  • Пока в списке есть стены:
    • Выберите случайную стену из списка. Если посещена только одна из двух ячеек, которые разделяет стена, то:
      • Сделайте стену проходом и отметьте непосещенную клетку как часть лабиринта.
      • Добавьте соседние стены ячейки в список стен.
    • Убрать стену из списка.

Код

neighbors(p::Point) = [Point(p.x, p.y+1), # up
                    Point(p.x, p.y-1), # down
                    Point(p.x-1, p.y), # left
                    Point(p.x+1, p.y)] # right

function newalls!(walls, p, maze, n, m)

    nbrs = neighbors(p)
    for a in nbrs
        if 1<a.x<n-1 && 1<a.y<m-1 && !maze[a.x,a.y]
            push!(walls, a) # Добавьте соседние стены ячейки в список стен.
        end
    end
end

function breakwall!(p, maze, n, m)

    nbrs = neighbors(p)
    # если среди соседей есть белая клетка
    if sum( a-> maze[a.x,a.y], nbrs) == 1
        for a in nbrs
            if  maze[a.x,a.y]
                # true =  белая
                p.x == a.x ? nx = p.x : p.x>a.x ? nx = p.x+1 : nx = p.x-1
                p.y == a.y ? ny = p.y : p.y>a.y ? ny = p.y+1 : ny = p.y-1
                maze[p.x,p.y] = true # соединить коридоры
                maze[nx,ny] = true
                p.x = nx
                p.y = ny
                return true
            end
        end
    else
        return false
    end
end

function prim(n, m)

    M = falses(n,m); # всё заполнено стенами
    p = Point(2, 2)
    M[p.x,p.y] = true

    walls = []
    newalls!(walls, p, M, n, m)

    while length(walls) != 0
        p = splice!( walls, rand(1:length(walls)) )

        if breakwall!(p, M, n, m)
            newalls!(walls, p, M, n, m)
        end

    end

    M
end

primaze = prim(19,19);
Gray.(primaze)

Джулия в лабиринте - 11

Получается более ветвисто и не менее потрясно, особенно процесс сборки.

А теперь имплементируем наиболее распространенный алгоритм нахождения кратчайшего маршрута:

Метод A*

  • Создается 2 списка вершин — ожидающие рассмотрения и уже рассмотренные. В ожидающие добавляется точка старта, список рассмотренных пока пуст.
  • Для каждой точки рассчитывается $H$ — примерное расстояние от точки до цели.
  • Из списка точек на рассмотрение выбирается точка с наименьшим $H$. Обозначим ее $X$.
  • Если $X$ — цель, то мы нашли маршрут.
  • Переносим $X$ из списка ожидающих рассмотрения в список уже рассмотренных.
  • Для каждой из точек, соседних для $X$ (обозначим эту соседнюю точку $Y$), делаем следующее:
    • Если $Y$ уже находится в рассмотренных — пропускаем ее.
    • Если $Y$ еще нет в списке на ожидание — добавляем ее туда.
  • Если список точек на рассмотрение пуст, а до цели мы так и не дошли — значит маршрут не существует.

Для начала зададим класс "точка" которая будет знать, как далеко она от цели:

mutable struct Point_h
    x::Int64 # horisont
    y::Int64 # vertical
    h::Float64

    Point_h(x, y) = new(x, y, 0.)
end

Теперь доопределим для структуры операцию сравнения, метод для установления наличия элемента в массиве, а также функции изъятия элемента, нахождения расстояния между точками и перечисления соседей:

Упрятано

import Base: in, ==

==(a::Point_h, b::Point_h) = a.x==b.x && a.y==b.y

function in(p::Point_h, Arr::Array{Point_h,1})
    for a in Arr
        if a == p
            return true
        end
    end
    return false
end

function splicemin!(Arr)#::Array{Point_h,1}
    i = argmin( [a.h for a in Arr] )
    splice!(Arr, i)
end

dista(u,v) = hypot(v.x-u.x, v.y-u.y) # <=> sqrt( (v.x-u.x)^2 + (v.y-u.y)^2 )

neighbors(p::Point_h) = [Point_h(p.x, p.y+1), # up
                    Point_h(p.x, p.y-1), # down
                    Point_h(p.x-1, p.y), # left
                    Point_h(p.x+1, p.y)] # right

Как всегда, непонятные операторы можно разъяснить с помощью команды ?, например ?splice, ?argmin.

И, собственно, сам метод A*

Код

function astar(M, start, final)
    # хорошая точка - не стена и не за границами
    isgood(p) = 1<p.x<n && 1<p.y<m && M[p.x,p.y] != 0

    n, m = size(M)
# как далеко от старта до цели
    start.h = dista(start,final)

    closed = []
    opened = []
    push!(opened, start)

    while length(opened) != 0

        X = splicemin!(opened)

        if X in closed
            continue
        end
        if X == final
            break
        end
        push!(closed, X)

        nbrs = neighbors(X)
        ygrex = filter(isgood, nbrs)

        for Y in ygrex

            if Y in closed
                continue
            else
                Y.h = dista(Y, final)
                push!(opened, Y)
            end
        end
    end
# возвращаем все посещенные
    closed # return
end

Загружаем картинку с лабиринтом и представляем ее в виде матрицы:

img0 = load("D:/dat/maze0.png") 
mazematrix = Float64.(channelview(img0))

И строим маршрут до выхода из произвольной точки:

s = Point_h(11,9) # start
f = Point_h(4,6) # finish

M = copy(mazematrix)
route = astar(M, s, f)

i = 1
for c in route
    # рисует маршрут
    M[c.x,c.y] = 0.7
    #save("D:/dat/Astar$i.png", M)
    i+=1
end
Gray.(M)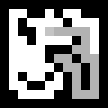

Джулия в лабиринте - 21

А поиск из всех позиций выглядит так:

Джулия в лабиринте - 22

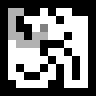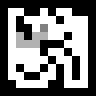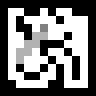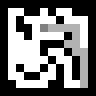
Видно, что агент прёт всегда стремится в сторону выхода и частенько заворачивает в тупики, что порождает лишние шаги, а запоминается-то весь маршрут. Это избегается чуть более сложным вариантом алгоритма А*

  • Создается 2 списка вершин — ожидающие рассмотрения и уже рассмотренные. В ожидающие добавляется точка старта, список рассмотренных пока пуст.
  • Для каждой точки рассчитывается $F=G + H$. $G$ — расстояние от старта до точки, $H$ — примерное расстояние от точки до цели. Так же каждая точка хранит ссылку на точку, из которой в нее пришли.
  • Из списка точек на рассмотрение выбирается точка с наименьшим $F$. Обозначим ее $X$.
  • Если $X$ — цель, то мы нашли маршрут.
  • Переносим $X$ из списка ожидающих рассмотрения в список уже рассмотренных.
  • Для каждой из точек, соседних для $X$ (обозначим эту соседнюю точку $Y$), делаем следующее:
    • Если $Y$ уже находится в рассмотренных — пропускаем ее.
    • Если $Y$ еще нет в списке на ожидание — добавляем ее туда, запомнив ссылку на $X$ и рассчитав $Y.G$ (это $X.G$ + расстояние от $X$ до $Y$) и $Y.H$.
    • Если же $Y$ в списке на рассмотрение — проверяем, если $X.G$ + расстояние от $X$ до $Y$ $< Y.G$, значит мы пришли в точку $Y$ более коротким путем, заменяем $Y.G$ на $X.G$ + расстояние от $X$ до $Y$, а точку, из которой пришли в $Y$ на $X$.
  • Если список точек на рассмотрение пуст, а до цели мы так и не дошли — значит маршрут не существует.

Но даже с лишними шагами наш вариант вполне укладывается в ограничение задачи, так что модификации программ будет вашим домашним заданием.

До конца олимпиады осталось всего-ничего, а нам нужно еще научиться переводить результаты работы наших алгоритмов в команды вида "RRLUUDL..."

И вот после всех этих хождений по лабиринтам, можно предположить, что решение гораздо проще. На самом деле простой вариант напрашивается сразу, но уж очень хотелось наделать красивых штук.

Если расположить нашего исполнителя в открытой местности и инициировать случайные блуждания, то он будет колебаться вблизи своей стартовой позиции. Но вот с введением стенок, часть направлений начнет гаситься, степеней свободы станет меньше, и с такими же входными данными агент переместится на большее расстояние.

Вот наш вариант проверки команд на пригодность к вызволению робота из лабиринта:

Код

M = [ 0  0  0  0  0  0  0  0  0  0  0  0
 0  1  1  0  0  1  0  1  1  0  0  0
 0  1  0  1  1  1  1  0  1  1  1  0
 0  1  0  0  1  9  1  1  1  1  1  0
 0  1  1  0  1  1  1  1  0  1  1  0
 0  1  1  1  1  0  0  0  1  1  1  0
 0  1  1  1  1  0  1  1  0  1  1  0
 0  1  1  1  1  1  0  1  1  0  1  0
 0  1  0  1  1  0  1  0  1  0  1  0
 0  1  1  0  0  1  1  0  1  0  1  0
 0  0  1  1  1  1  0  0  1  1  1  0
 0  0  0  0  0  0  0  0  0  0  0  0]

mutable struct Point # point
    x::Int64 # vertical
    y::Int64 # horisont
    Point(x, y) = new(x, y)
end

function isexit(str, c)

    try
        for s in str
            if s == 'R'
                c.y+=M[c.x, c.y+1];

            elseif s == 'L' 
                c.y-=M[c.x, c.y-1];

            elseif s == 'U'
                c.x+=M[c.x+1, c.y];

            elseif s == 'D'
                c.x-=M[c.x-1, c.y];

            else
                 println("Error! Use only R, L, U, D")
            end

        end
    catch
        return true
    end
    return false
end

function test(Str)
    k = 0
    n, m = 10,10
    for i in 2:m+1, j in 2:n+1
        if M[i,j] == 1
            c = Point(i, j)
            a = isexit(S,c)
            if a
                k +=1
                #println(a)
            end
        end
    end
    println(k, " test completed from ", sum(M)-9)
end

Теперь достаточно генерировать случайные строки, пока не получится та, что сработает для всех стартовых позиций:

using Random
S = randstring("RLUD",200)

"RDRRRDLRLUULURUDUUDLLLLLULLUDRRURDLDLULLRLUUUDURUUUULRUDUURUUDLRLLULRLUDRRLRRULLDULRRRRULRLLDULRLDRUDURDRUUDUUDDDDDLURRRRDRDURRRDDLLDUURRRLDRUDLRLLRDDRLRRRDDLLLRUURDRLURDLLUULLLLUURLLULUDULDDLDLLRLDUD"

test(S)
41 test completed from 70

К тому же, можно было и не заморачиваться на счет теста. Достаточно было прочитать задание и сгенерировать рандомную максимально допустимую условием строку:

for i in 1:20
    S = randstring("RLUD",1000)
    test(S)
end

70 test completed from 70
70 test completed from 70
70 test completed from 70
70 test completed from 70
55 test completed from 70#
65 test completed from 70#
70 test completed from 70
70 test completed from 70
38 test completed from 70#
70 test completed from 70
70 test completed from 70
56 test completed from 70#
70 test completed from 70
70 test completed from 70
70 test completed from 70
16 test completed from 70#
70 test completed from 70
24 test completed from 70#
70 test completed from 70
70 test completed from 70

То есть с вероятностью в 70% строка прошла бы тесты.

На этом всё. Желаю читателю удачного рандома, терпения и интуиции на очевидные решения.

Для любознательных — ссылки для углубления в тему:

Автор: Yermack

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js