Всем привет! Сегодня я расскажу о своих экспериментах с системами частиц. Основной целью было нахождение простых правил, которые бы порождали интересное поведение.
Классический пример системы с простыми правилами и сложным поведением — клеточные автоматы, именно на них я и ориентировался, пытаясь подобрать правила. Конечно же, для клеточных автоматов правила будут в большинстве случаев проще. Но частицы могут быть красивее!
Под катом много мегабайт гифок.
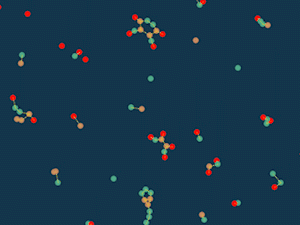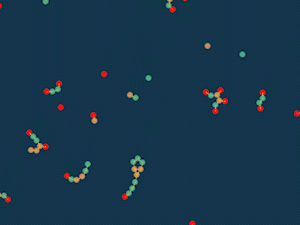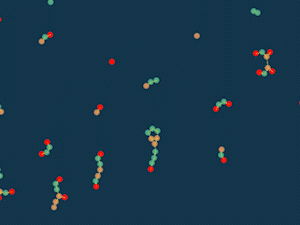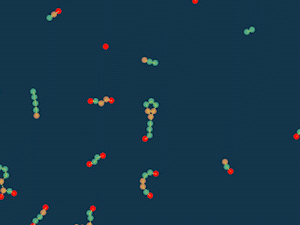
Клеточный суп
Сначала я пошёл по стопам игры «жизнь»: у каждой частицы есть счётчик “перенаселения”, который равен сумме обратных квадратов расстояний до других частиц. Если этот счётчик меньше определённого предела, то есть соседей мало, то частица притягивается к другим частицам, а если соседей много — отталкивается. Если частицы пересекаются, то они отталкиваются в любом случае, чтобы не проходить сквозь друг друга.
Случайно раскидываем частицы по полю и смотрим, что выйдет.

Интересно, что получается что-то похожее на клетки и выглядит уже довольно живо. Можно, например, добавить больше типов частиц. Пусть разные частицы будут по-разному увеличивать число соседей, а какие-то даже смогут его уменьшать.

Теперь наши “клетки” стали многослойными.
Минус подобных правил в том, что получаются довольно хаотичные не очень устойчивые структуры.
Поэтому идём дальше.
Игра в догонялки
Меняем правила игры. Больше не будем считать соседей. Пусть частицы будут просто притягиваться или отталкиваться в зависимости от их типов. Если все частицы одного типа, то тут всего 2 варианта: они либо все отталкиваются, либо все притягиваются.

Если есть больше типов частиц, то тут можно комбинировать, какие к каким будут притягиваться, а от каких отталкиваться.
Любое такое правило можно представить в виде матрицы N*N, где N — количество типов частиц, а в каждой ячейке либо притяжение, либо отталкивание. Притяжение обозначим за 0, а отталкивание — за 1. Тогда любая матрица соответствует определённому числу, например, матрица $inline$begin{bmatrix} 1 & 0\ 1 & 0 end{bmatrix}$inline$ будет означать 0101, то есть 5 (последняя цифра в двоичном виде — первая в матрице). Количество различных матриц для правил равно $inline$2^{N^2}$inline$. Например, для двух типов частиц получится 16 правил.
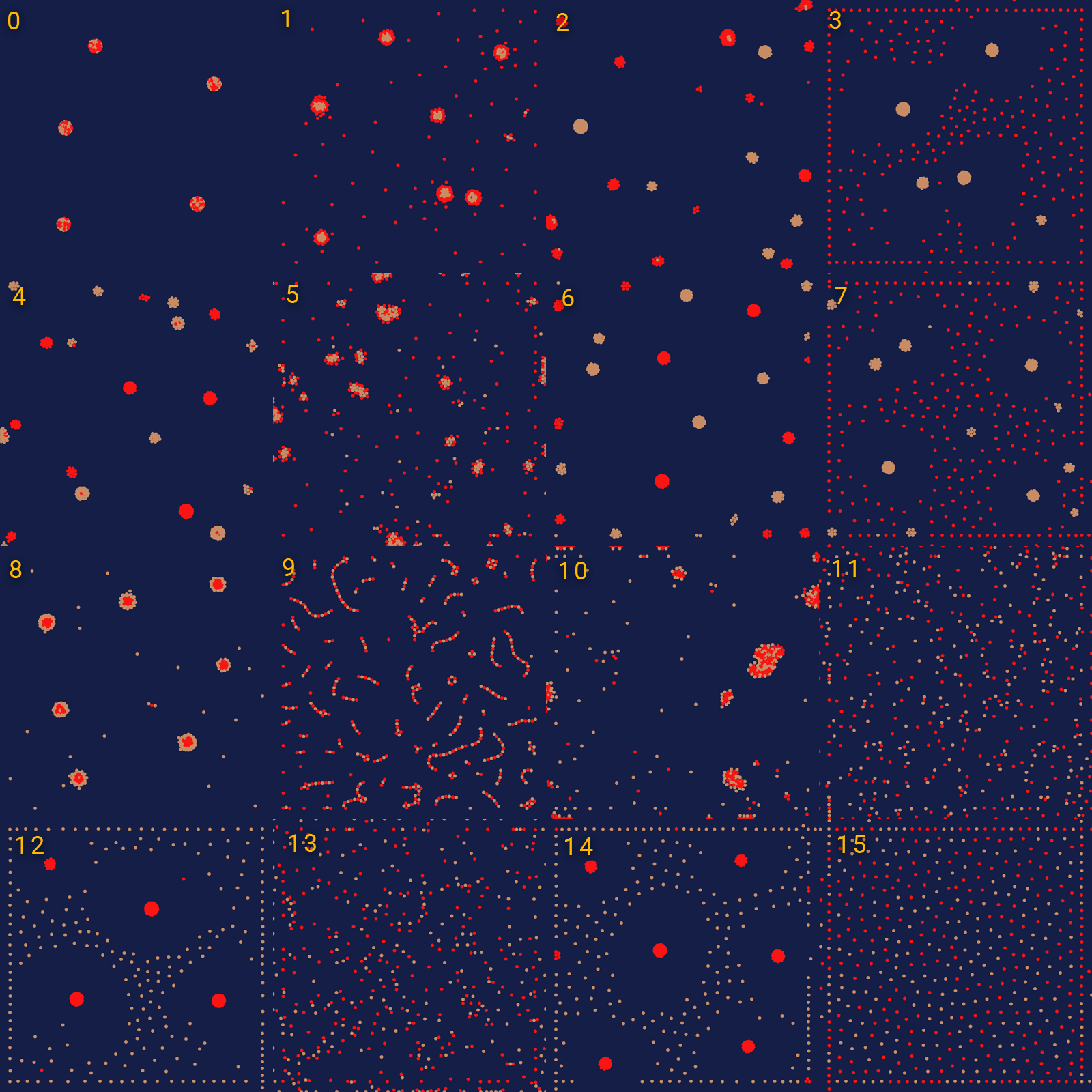
Может показаться, что правило 3 такое же, как правило 7, но если перевести их в матрицы, то получится $inline$begin{bmatrix} 1 & 1\ 0 & 0 end{bmatrix}$inline$ и $inline$begin{bmatrix} 1 & 1\ 1 & 0 end{bmatrix}$inline$, а это значит, что в правиле 7 только бежевые притягиваются друг к другу. В то время как в правиле 3, бежевые притягиваются еще и к красным. Но из-за низкой плотности красных это оказывает малозаметный эффект. По-настоящему же одинаковыми правилами можно назвать, например, 3 и 12, так как всё поведение частиц идентично, только цвета поменялись местами. Если оставить только правила с уникальным поведением, то из 16 правил у нас останется 10. Для трёх типов частиц из 512 возможных комбинаций остаётся 104 уникальных, а для четырёх — 3044 из 65536 Получается последовательность 2, 10, 104, 3044.
Но вернёмся к нашим десяти правилам.

В глаза бросается правило 9, которое является матрицей $inline$begin{bmatrix} 1 & 0\ 0 & 1 end{bmatrix}$inline$, где одинаковые отталкиваются, а разные притягиваются. Случайно разбросанные частицы быстро образуют “нити” и на этом застывают.
Так же застывают правила 1 и 15: они эквивалентны двум единственным правилам для одного типа частиц (предыдущая анимированная гифка). Обычно застывают все правила, матрицы которых симметричны. Еще есть правила 2, 3, 5, и 11 с несимметричными матрицами. Это значит, что один вид частиц притягивается, ко второму, а второй отталкивается от первого. Начинаются “догонялки”.

Правило 3 слишком стабильное, в нём “догонялки” в какой-то момент прекращаются, а если и возобновляются, то редко и ненадолго. Правило 11 — слишком хаотичное. Остаются 2 и 5.
Можно их как-то скомбинировать, чтобы было еще интереснее. Я подобрал правило 105 для трёх цветов, то есть матрицу $inline$begin{bmatrix} 1 & 0 & 0\ 1 & 0 & 1\ 1 & 0 & 0 end{bmatrix}$inline$, и такое вот поведение:

Это всё выглядит живо, но неустойчиво. А как же определённые повторяющиеся “живые” существа? Как же поиск осцилляторов и глайдеров? Надо снова менять правила!
Плавающая жизнь
Не будем сильно менять правила. Вместо этого добавим новую фичу. Теперь частицы на небольшом расстоянии будут образовывать связи. Если частицы связаны, то они постоянно притягиваются друг к другу. Это притяжение не ослабевает с расстоянием. Но, если расстояние выше определённого порога, то связь рвётся.
Я попробовал разные варианты с тремя цветами и остановился на том, где красные могут образовывать только одну связь, бежевые — три, а голубые — две, то есть можно обозначить максимальные связи в виде $inline$begin{bmatrix} 1\ 3\ 2 end{bmatrix}$inline$.
При этом, красные не могут связываться с другими красными, бежевые и голубые могут иметь не больше двух связей с частицами своего цвета и не больше одной с частицами каждого другого цвета. Это всё в виде матрицы: $inline$begin{bmatrix} 0 & 1 & 1\ 1 & 2 & 1\ 1 & 1 & 2 end{bmatrix}$inline$

Я поигрался с разными правилами притягивания/отталкивания, и мне понравилось $inline$begin{bmatrix} 1 & 1& 0\ 1 & 1 & 1\ 1 & 1 & 1end{bmatrix}$inline$, то есть красные притягиваются к голубым, а во всех остальных случаях все отталкиваются.

Кажется, будто эти существа плавают в жидкости или машут крыльями.


Пара осцилляторов и пара глайдеров.
Неподвижные фигуры легко получить: нужно лишь не использовать красный и голубой вместе, так как в этих правилах это единственная комбинация с притяжением.


Но иногда движение возникает и при таких цветах. Некоторые фигуры начинают раскручиваться, отталкиваясь от других, получаются “шестерёнки”.
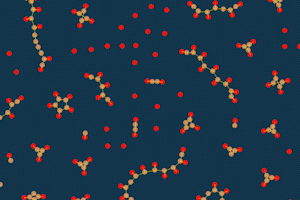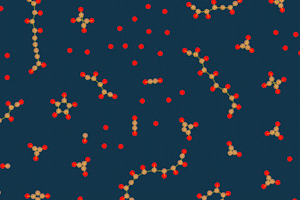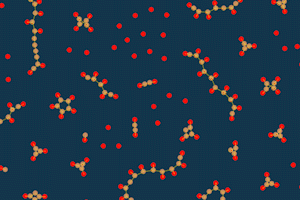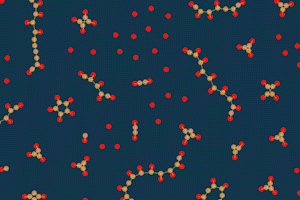
Заключение
В дальнейшем было бы интересно сравнивать полученные фигуры, собрать статистику по частоте их появления.
Еще можно эти правила использовать как основу для создания более сложных существ с едой, размножением, эволюцией.
Можно построить из этого логические схемы, собрать калькулятор, процессор лучше не надо.
Автор: Onigiri