Julia, Градиентный спуск и симплекс метод

в 17:46, , рубрики: Julia, Алгоритмы, градиентный спуск, машинное обучение, метод Нелдера-Мида, многомерная оптимизация, покоординатный спуск, Программирование, симлекс метод

Julia, Градиентный спуск и симплекс метод - 1

Продолжаем знакомство с методами многомерной оптимизации.

Далее предложена реализация метода наискорейшего спуска с анализом скорости выполнения, а также имплементация метода Нелдера-Мида средствами языка Julia и C++.

Метод градиентного спуска

Поиск экстремума ведется шагами в направлении градиента (max) или антиградиента (min). На каждом шаге в направлении градиента (антиградиента) движение осуществляется до тех пор, пока функция возрастает (убывает).

За теорией пройдитесь по ссылкам:

Модельной функцией выберем эллиптический параболоид и зададим функцию отрисовки рельефа:

using Plots
plotly() # интерактивные графики

function plotter(plot_fun; low, up)
    Xs = range(low[1], stop = up[1], length = 80)
    Ys = range(low[2], stop = up[2], length = 80)
    Zs = [ fun([x y]) for x in Xs, y in Ys ];

    plot_fun(Xs, Ys, Zs)
    xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) # линовка осей
    yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] )
end

parabol(x) = sum(u->u*u, x) # сумма квадратов
fun = parabol
plotter(surface, low = [-1 -1], up = [1 1])

Julia, Градиентный спуск и симплекс метод - 2

Зададим функцию реализующую метод наискорейшего спуска, которая принимает размерность задачи, точность, длину шага, начальное приближение и размеры рамки ограничивающей график:

# точка-с-запятой значит, что все последующие параметры - ключевые слова
function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10])
    k = 0

    while st > ε
        g = grad(fit, 0.01)
        fung = fun(fit)

        fit -= st*g

        if fun(fit) >= fung
            st *= 0.5
            fit += st*g
        end

        k += 1
        #println(k, " ", fit)
    end
    #println(fun(fit))
end

На функции вычисляющей направление градиента можно заостриться в плане оптимизации.

Первое, что идет на ум — это действия с матрицами:

# delta - приращение аргумента используемое для вычисления
# производных по формуле центральных разностей
function grad(fit, δ)

    ndimes = length(fit)
    Δ = zeros(ndimes, ndimes)

    for i = 1:ndimes
        Δ[i,i] = δ
    end

    fr = [ fun( fit + Δ[:,i] ) for i=1:ndimes]
    fl = [ fun( fit - Δ[:,i] ) for i=1:ndimes]

    g = 0.5(fr - fl)/δ

    modg = sqrt( sum(x -> x*x, g) )

    g /= modg
end

Чем действительна хороша Julia, так это тем, что проблемные места легко можно потестить:

#]add BenchmarkTools
using BenchmarkTools

@benchmark ofGradient()

BenchmarkTools.Trial: 
  memory estimate:  44.14 KiB
  allocs estimate:  738
  --------------
  minimum time:     76.973 μs (0.00% GC)
  median time:      81.315 μs (0.00% GC)
  mean time:        92.828 μs (9.14% GC)
  maximum time:     5.072 ms (94.37% GC)
  --------------
  samples:          10000
  evals/sample:     1

Можно кинуться перепечатывать всё в Сишном стиле

function grad(fit::Array{Float64,1}, δ::Float64)

    ndimes::Int8 = 2
    g = zeros(ndimes)
    modg::Float64 = 0.
    Fr::Float64 = 0.
    Fl::Float64 = 0.

    for i = 1:ndimes
        fit[i] += δ
        Fr = fun(fit)
        fit[i] -= 2δ
        Fl = fun(fit)
        fit[i] += δ

        g[i] = 0.5(Fr - Fl)/δ
        modg += g[i]*g[i]
    end

    modg = sqrt( modg )

    g /= modg
end

@benchmark ofGradient()

BenchmarkTools.Trial: 
  memory estimate:  14.06 KiB
  allocs estimate:  325
  --------------
  minimum time:     29.210 μs (0.00% GC)
  median time:      30.395 μs (0.00% GC)
  mean time:        33.603 μs (6.88% GC)
  maximum time:     4.287 ms (98.88% GC)
  --------------
  samples:          10000
  evals/sample:     1

Но как оказывается, оно само и без нас знает, какие типы надо ставить, так что приходим к компромиссу:

function grad(fit, δ) # вычисляет направление градиента

    ndimes = length(fit)
    g = zeros(ndimes)

    for i = 1:ndimes
        fit[i] += δ
        Fr = fun(fit)
        fit[i] -= δ

        fit[i] -= δ
        Fl = fun(fit)
        fit[i] += δ

        g[i] = 0.5(Fr - Fl)/δ
    end

    modg = sqrt( sum(x -> x*x, g) )

    g /= modg
end

@benchmark ofGradient()

BenchmarkTools.Trial: 
  memory estimate:  15.38 KiB
  allocs estimate:  409
  --------------
  minimum time:     28.026 μs (0.00% GC)
  median time:      30.394 μs (0.00% GC)
  mean time:        33.724 μs (6.29% GC)
  maximum time:     3.736 ms (98.72% GC)
  --------------
  samples:          10000
  evals/sample:     1

А теперь пусть рисует:

function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10])
    k = 0
    x = []
    y = []
    push!(x, fit[1])
    push!(y, fit[2])
    plotter(contour, low = low, up = up)

    while st > ε
        g = grad(fit, 0.01)
        fung = fun(fit)

        fit -= st*g

        if fun(fit) >= fung
            st *= 0.5
            fit += st*g
        end

        k += 1
        #println(k, " ", fit)
        push!(x, fit[1])
        push!(y, fit[2])
    end
    plot!(x, y, w = 3, legend = false, marker = :rect )
    title!("Age = $k f(x,y) = $(fun(fit))")
    println(fun(fit))
end

ofGradient()

Julia, Градиентный спуск и симплекс метод - 3

А теперь опробуем на функции Экли:

ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ
# f(0,0) = 0, x_i ∈ [-5,5]

fun = ekly

ofGradient(fit = [4.3, 4.9], st = 0.1, low = [3 4.5], up = [4.5 5.4] )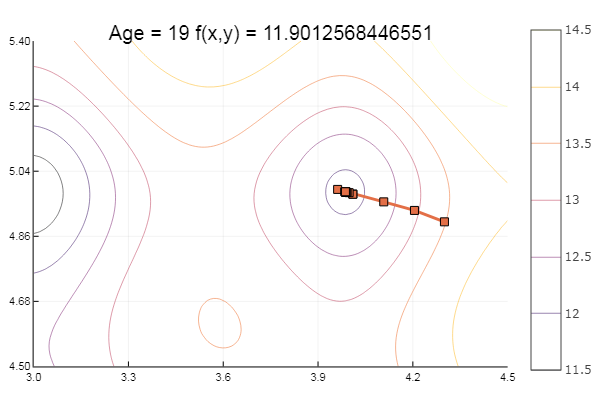

Julia, Градиентный спуск и симплекс метод - 4

Свалилось в локальный минимум. Сделаем-ка шаги побольше:

ofGradient(fit = [4.3, 4.9], st = 0.9, low = [3 4.5], up = [4.5 5.4] )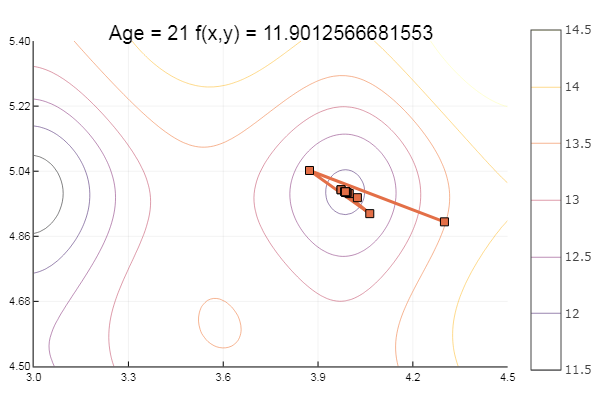

Julia, Градиентный спуск и симплекс метод - 5

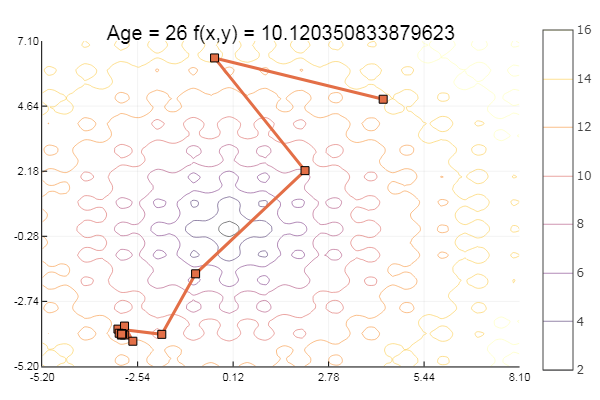
ofGradient(fit = [4.3, 4.9], st = 1.9, low = [-5.2 -2.2], up = [8.1 7.1] )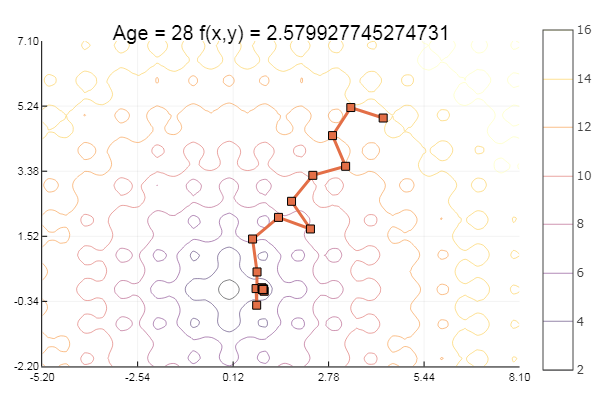

Julia, Градиентный спуск и симплекс метод - 6

… и еще немного:

ofGradient(fit = [4.3, 4.9], st = 8.9, low = [-5.2 -2.2], up = [8.1 7.1] )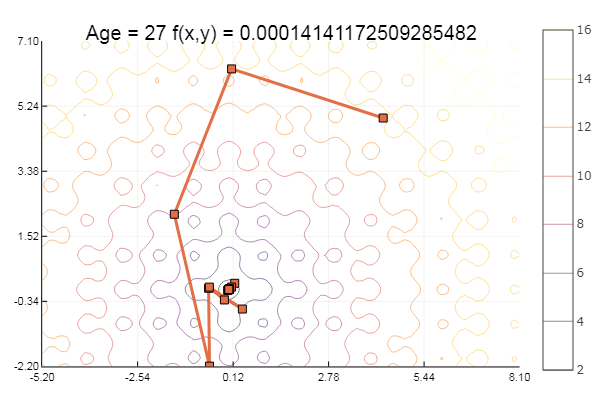

Julia, Градиентный спуск и симплекс метод - 7
Отлично! А теперь что-нибудь с оврагом, например функцию Розенброка:

rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 
# f(0,0) = 0, x_i ∈ [-5,5]
fun = rosenbrok
plotter(surface, low = [-2 -1.5], up = [2 1.5])

Julia, Градиентный спуск и симплекс метод - 8

ofGradient(fit = [2.3, 2.2], st = 9.9, low = [-5.2 -5.2], up = [8.1 7.1] )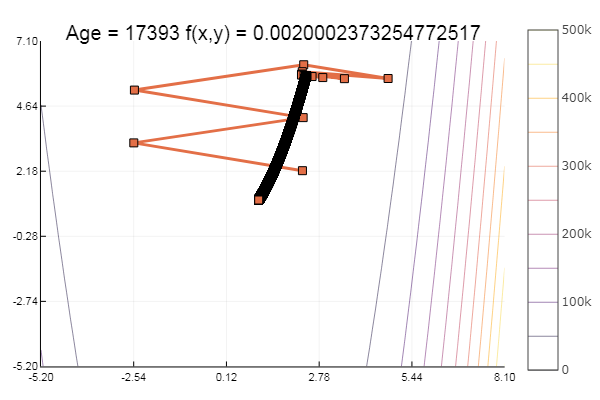

Julia, Градиентный спуск и симплекс метод - 9

ofGradient(fit = [2.3, 2.2], st = 0.9, low = [-5.2 -5.2], up = [8.1 7.1] )

Julia, Градиентный спуск и симплекс метод - 10
Мораль: градиенты не любят пологостей.

Симплекс метод

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной(точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс.

Вспомогательные функции:

#сортировка столбцов матрицы выстраиванием элементов последней строки в порядке возрастания
function sortcoord(Mx)
    N = size(Mx,2)
    f = [fun(Mx[:,i]) for i in 1:N] # значение функции в вершинах
    Mx[:, sortperm(f)]
#Return a permutation vector I that puts v[I] in sorted order.
end
# Норма матрицы
function normx(Mx)
    m = size(Mx,2)
    D = zeros(m-1,m)
    vecl(x) = sqrt( sum(u -> u*u, x) )# длина вектора

    for i = 1:m, j = i+1:m
        D[i,j] = vecl(Mx[:,i] - Mx[:,j]) # считает длину разности столбцов
    end
    D
    sqrt(maximum(D))
end

function simplexplot(xy, low, up)
    for i = 1:length(xy)
        if i%11 == 0
            low *= 0.05
            up *= 0.05
        end

        Xs = range(low[1], stop = up[1], length = 80)
        Ys = range(low[2], stop = up[2], length = 80)
        Zs = [ fun([x y]) for y in Ys, x in Xs ]

        contour(Xs, Ys, Zs)
        xaxis!( low[1]:(up[1]-low[1])*0.2:up[1] )
        yaxis!( low[2]:(up[2]-low[2])*0.2:up[2] )

        plot!(xy[i][1,:], xy[i][2,:], w = 3, legend = false, marker = :circle )
        title!("Age = $i f(x,y) = $(fun(xy[i][:,1]))")
        savefig("$fun $i.png")
    end
end

И сам симплекс метод:

function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1])

    vecl(v) = sqrt( sum(x -> x*x, v) )

    k = 0
    N = ndimes
    dz = zeros(N, N+1)
    Xx = zeros(N, N+1)
    coords = []

    for i = 1:N+1
        Xx[:,i] = fit
    end

    for i = 1:N
        dz[i,i] = 0.5*vecl(fit)
    end

    Xx += dz

    p = normx(Xx)

    while p > ε

        k += 1
        Xx = sortcoord(Xx)

        Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] # среднее эл-тов i-й строки
        Ro = 2Xo - Xx[:,N+1]
        FR = fun(Ro)

        if FR > fun(Xx[:,N+1])
            for i = 2:N+1
                Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i])
            end     
        else
            if FR < fun(Xx[:,1])

                Eo = Xo + 2(Xo - Xx[:,N+1])

                if FR > fun(Eo)
                    Xx[:,N+1] = Eo
                else
                    Xx[:,N+1] = Ro
                end
            else
                if FR <= fun(Xx[:,N])
                    Xx[:,N+1] = Ro
                else
                    Co = Xo + 0.5(Xo - Xx[:,N+1])

                    if FR > fun(Co)
                        Xx[:,N+1] = Co
                    else
                        Xx[:,N+1] = Ro
                    end
                end
            end
        end

        #println(k, " ", p, " ", Xx[:,1])
        push!(coords, [Xx[:,1:3] Xx[:,1] ])
        p = normx(Xx)

    end #while 

    #simplexplot(coords, low, up)
    fit = Xx[:,1]
end

ofNelderMid(fit = [-9, -2], low = [-2 2], up = [-8 8])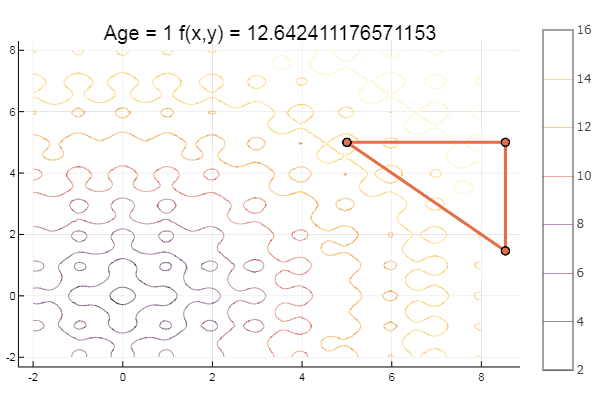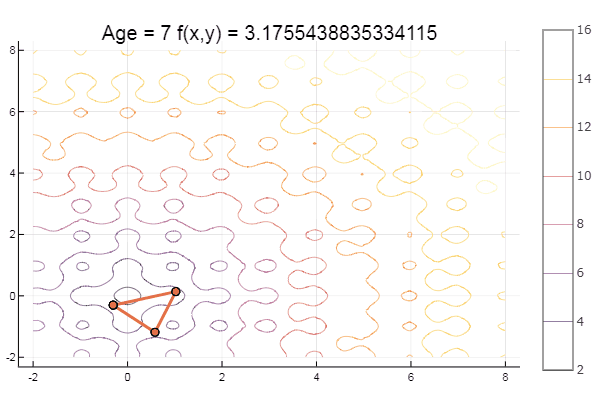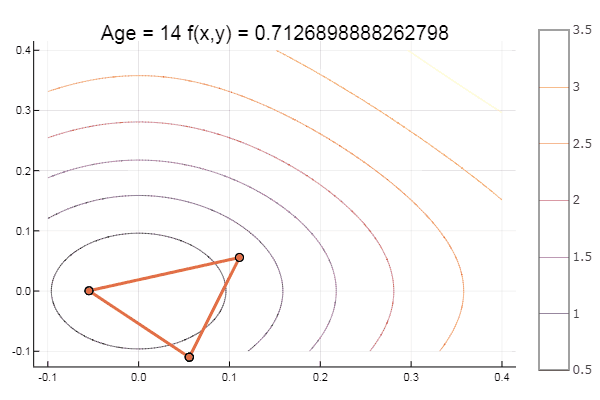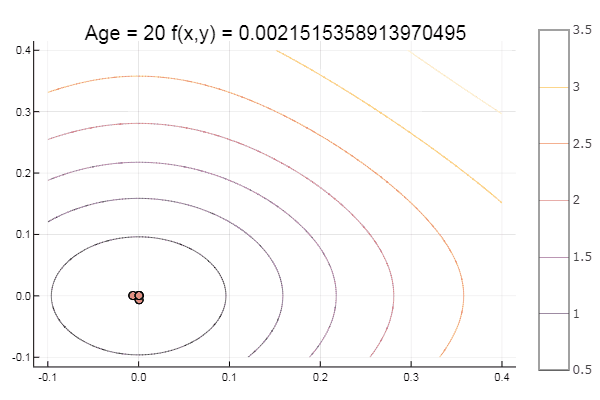

Julia, Градиентный спуск и симплекс метод - 11

И на десерт какую-нибудь буку… например функцию Букина
$f(x,y)=100sqrt{|y-0.01x^2|} + 0.01|x+10|$

bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) 
# f(-10,1) = 0, x_i ∈ [-15,-5; -3,3]
fun = bukin6
ofNelderMid(fit = [-10, -2], low = [-3 -7], up = [-8 -4.5])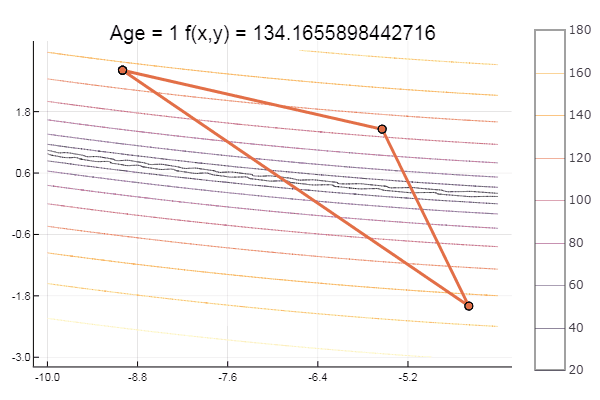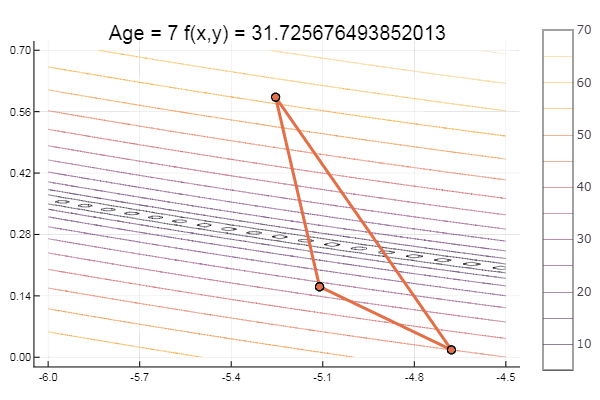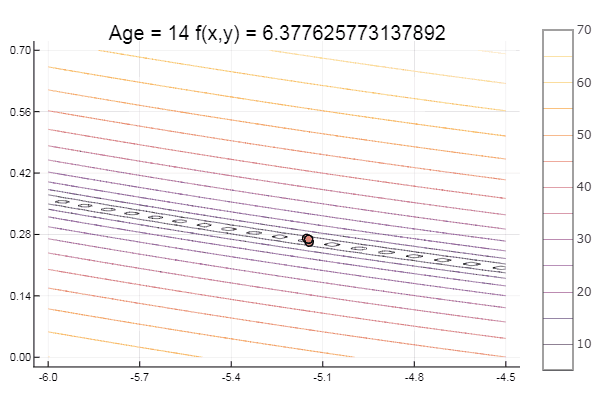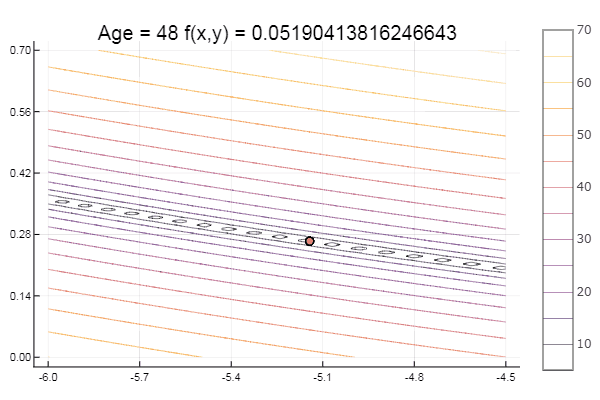

Julia, Градиентный спуск и симплекс метод - 13

Локальный минимум — ну ничего, главное правильно подобрать стартовый симплекс, так что для себя я нашел фаворита.

Бонус. Методы Нелдера-Мида, наискорейшего спуска и покоординатного спуска на С++

Аларма! 550 строк кода!

/* 
 * File:   main.cpp
 * Author: User
 *
 * Created on 3 сентября 2017 г., 21:22
 */

#include <iostream>
#include <math.h>

using namespace std;

typedef double D;

class Model
{
public:
    D *fit;
    D ps;

    Model();
    D I();
};

Model :: Model()
{
    ps = 1;
    fit = new D[3];

    fit[0]=1.3;
    fit[1]=1.;
    fit[2]=2.;
}

D Model :: I() // rosenbrock
{
    return 100*(fit[1]-fit[0]*fit[0]) * (fit[1]-fit[0]*fit[0]) + (1-fit[0])*(1-fit[0]);
}

class Methods : public Model
{
public:
    void ofDescent();
    void Newton(int i);
    void SPI(int i); //sequential parabolic interpolation
    void Cutters(int i);
    void Interval(D *ab, D st, int i);
    void Gold_section(int i);
    void ofGradient();
    void Grad(int N, D *g, D delta);
    void Srt(D **X, int N);
    void ofNelder_Mid();
    D Nor(D **X, int N);
};

void Methods :: ofDescent()//метод покоординатного спуска
{
    int i, j=0;
    D *z = new D[3];
    D sumx, sumz;
    sumx = sumz = 0;

    do
    {
        sumx = sumz = 0;

        for(i=0; i<3; i++)
            z[i] = fit[i];

        for(i=0; i<2; i++)
        {
            //Cutters(i);
            //SPI(i);
            Newton(i);
            //Gold_section(i);

            sumx += fit[i];
            sumz += z[i];
        }
        j++;
        //if(j%1000==0)
            cout << j << " " << fit[0] << "  " << fit[1] << "  " << fit[2] << " " << fit[3] << endl;
        //cout << sumz << "  " << sumx << endl;
    }
    while(fabs(sumz - sumx) > 1e-6);

    delete[]z;
}

void Methods :: SPI(int i)
{
    int k = 2;
    D f0, f1, f2;
    D v0, v1, v2;
    D s0, s1, s2;
    D *X = new D[300];
    X[0] = fit[i] + 0.01;
    X[1] = fit[i];
    X[2] = fit[i] - 0.01;

    while(fabs(X[k] - X[k-1]) > 1e-3)
    {
        fit[i] = X[k];
        f0 = I();
        fit[i] = X[k-1];
        f1 = I();
        fit[i] = X[k-2];
        f2 = I();

        v0 = X[k-1] - X[k-2];
        v1 = X[k  ] - X[k-2];
        v2 = X[k  ] - X[k-1];
        s0 = X[k-1]*X[k-1] - X[k-2]*X[k-2];
        s1 = X[k  ]*X[k  ] - X[k-2]*X[k-2];
        s2 = X[k  ]*X[k  ] - X[k-1]*X[k-1];

        X[k+1] = 0.5*(f2*s2 - f1*s1 + f0*s0) / (f2*v2 - f1*v1 + f0*v0);
        k++;
        cout << k << "  " << X[k] << endl;
    }
    fit[i] = X[k];

    delete[]X;
}

void Methods :: Newton(int i)
{
    D dt, T, It;
    int k=0;

    while(fabs(T-fit[i]) > 1e-3)
    {
        It = I();
        T = fit[i];
        fit[i] += 0.01;
        dt = I();
        fit[i] -= 0.01;

        fit[i] -= It*0.001 / (dt - It);
        cout << k << "  " << fit[i] << endl;
        k++;
    }
}

void Methods :: Cutters(int i)
{
    D Tn, Tnm, Tnp, It, Itm;
    int j=0;

    Tn  = 0.15;
    Tnm = 2.65;//otrezok
    Itm = I();
    //cout << Tnm << "  " << Tn << endl;

    while(fabs(Tn-Tnm) > 1e-6)
    {
        fit[i] = Tn;
        It  = I();
        Tnp = Tn - It * (Tn-Tnm) / (It-Itm);
        cout << j+1 << " " << Tnp << endl;
        Itm = It;
        Tnm = Tn;
        Tn = Tnp;
        j++;
    }
    fit[i] = Tnp;
}

void Methods :: Interval(D *ab, D st, int i)
{
    D Fa, Fdx, d, c, Fb, fitbox = fit[i];

    ab[0] = fit[i];
    Fa = I();
    fit[i] -= st;
    Fdx = I();
    fit[i] += st;
    if(Fdx < Fa)
        st = -st;

    fit[i] += st;
    ab[1] = fit[i];
    Fb = I();

    while(Fb < Fa)
    {
        d = ab[0];
        ab[0] = ab[1];
        Fa = Fb;
        fit[i] += st;
        ab[1] = fit[i];
        Fb = I();
        cout << Fb << " " << Fa << endl;
    }

    if(st<0)
    {
        c = ab[1];
        ab[1] = d;
        d = c;
    }

    ab[0] = d;
    fit[i] = fitbox;
}

void Methods :: Gold_section(int i)
{
    D Fa, Fb, al, be;
    D *ab = new D[2];
    D st = 0.5;
    D e = 0.5*(sqrt(5) - 1);
    Interval(ab, st, i);

    al = e*ab[0] + (1-e)*ab[1];
    be = e*ab[1] + (1-e)*ab[0];

    fit[i] = al;
    Fa = I();
    fit[i] = be;
    Fb = I();

    while(fabs(ab[1]-ab[0]) > e)
    {
        if(Fa < Fb)
        {
            ab[1] = be;
            be = al;
            Fb = Fa;
            al = e*ab[0] + (1-e)*ab[1];
            fit[i] = al;
            Fa = I();
        }
        if(Fa > Fb)
        {
            ab[0] = al;
            al = be;
            Fa = Fb;
            be = e*ab[1] + (1-e)*ab[0];
            fit[i] = be;
            Fb = I();
        }
    cout << ab[0] << " " << ab[1] << endl;
    }
    fit[i] = 0.5*(ab[0] + ab[1]);
    cout << ab[0] << " " << ab[1] << endl;
}

void Methods :: Grad(int N, D *g, D delta)//вектор направления градиента
{
    int n;
    D Fr, Fl, modG=0;

    for(n=0; n<N; n++)
    {
        fit[n] += delta;
        Fr = I();
        fit[n] -= delta;

        fit[n] -= delta;
        Fl = I();
        fit[n] += delta;

        g[n] = (Fr - Fl)*0.5/delta;
        modG += g[n]*g[n];
    }
    modG = sqrt(modG);

    for(n=0; n<N; n++)
        g[n] /= modG;

    g[N] = I();
}

void Methods :: ofGradient()
{
    int n, j=0;
    D Fun, st, eps;
    const int N = 2;
    D *g = new D[N+1];

    st = 0.1;
    eps = 0.000001;

    while(st > eps)
    {
        Grad(N,g,0.0001);
        for(n=0; n<N; n++)
            fit[n] -= st*g[n];

        Fun = I();
        if(Fun >= g[N])
        {
            st /= 2.;
            for(n=0; n<N; n++)
                fit[n] += st*g[n];
        }
        j++;
        cout << j << " " << fit[0]/ps << "  " << fit[1]/ps << "  " << fit[2]/ps<< endl;
    }
}

void Methods :: ofNelder_Mid()
{
    int i, j, k;
    D modz = 0., p, eps = 1e-3;
    D FR, FN, F0, FE, FNm1, FC;
    const int N = 2;
    D *Co = new D[N];
    D *Eo = new D[N];
    D *Ro = new D[N];
    D *Xo = new D[N];
    D **Xx = new D*[N];
    D **dz = new D*[N];
    for(i=0;i<N;i++)
    {
        dz[i] = new D[N];
        Xx[i] = new D[N+1];
    }

    for(i=0;i<N;i++)
        for(j=0;j<N;j++)
            if(i^j)
                dz[i][j] = 0;
            else
                dz[i][j] = 1;

    for(i=0;i<N;i++)
       Xx[i][N] = fit[i];

    for(i=0;i<N;i++)
        modz += fit[i]*fit[i];
    modz = sqrt(modz);

    for(i=0;i<N;i++)
        dz[i][i] = 0.5*modz;

    for(i=0;i<N;i++)
        for(j=0;j<N;j++)
            Xx[i][j] = fit[i] + dz[i][j];

    k = 0;
    p = Nor(Xx, N);

    while(p > eps)
    {
        k++;
        Srt(Xx, N);

        for(i=0;i<N;i++)
            Xo[i] = 0.;

        for(i=0;i<N;i++)
            for(j=0;j<N;j++)
                Xo[i] += Xx[i][j];

        for(i=0;i<N;i++)
            Xo[i] /= N;

        for(i=0;i<N;i++)
            Ro[i] = Xo[i] + (Xo[i]-Xx[i][N]);

        for(i=0;i<N;i++)
            fit[i] = Ro[i];

        FR = I();

        for(i=0;i<N;i++)
            fit[i] = Xx[i][N];

        FN = I();

        if(FR > FN)
        {
            for(i=0;i<N;i++)
                for(j=1;j<=N;j++)
                    Xx[i][j] = 0.5*(Xx[i][0] + Xx[i][j]);
        }
        else
        {
            for(i=0;i<N;i++)
                fit[i] = Xx[i][0];
            F0 = I();

            if(FR < F0)
            {
                for(i=0;i<N;i++)
                    Eo[i] = Xo[i] +2*(Xo[i] - Xx[i][N]);

                for(i=0;i<N;i++)
                    fit[i] = Eo[i];

                FE = I();

                if(FE < FR)
                    for(i=0;i<N;i++)
                        Xx[i][N] = Eo[i];
                else
                    for(i=0;i<N;i++)
                        Xx[i][N] = Ro[i];
            }
            else
            {
                for(i=0;i<N;i++)
                    fit[i] = Xx[i][N-1];

                FNm1 = I();

                if(FR <= FNm1)
                    for(i=0;i<N;i++)
                        Xx[i][N] = Ro[i];

                else
                {
                    for(i=0;i<N;i++)
                        Co[i] = Xo[i] +0.5*(Xo[i] - Xx[i][N]);

                    for(i=0;i<N;i++)
                        fit[i] = Co[i];

                    FC = I();

                    if(FC < FR)
                        for(i=0;i<N;i++)
                            Xx[i][N] = Co[i];
                    else
                        for(i=0;i<N;i++)
                            Xx[i][N] = Ro[i];
                }
            }
        }

        for(i=0;i<N;i++)
            cout << Xx[i][0] << " ";
        cout << k << " " << p << endl;

        p = Nor(Xx, N);

        if(p < eps)
            break;
    }

    for(i=0;i<N;i++)
        fit[i] = Xx[i][0];

    /*for(i=0;i<N;i++)
    {
        for(j=0;j<N+1;j++)
            cout << Xx[i][j] << " ";
        cout << endl;
    }*/

    delete[]Co;
    delete[]Xo;
    delete[]Ro;
    delete[]Eo;
    for(i=0;i<N;i++)
    {
        delete[]dz[i];
        delete[]Xx[i];
    }
}
//возвращает норму вектора
D Methods :: Nor(D **X, int N)
{
    int i, j, k;
    D norm, xij, pn = 0.;

    for(i=0;i<N;i++)
        for(j=i+1;j<=N;j++)
            {
                xij = 0.;
                for(k=0;k<N;k++)
                    xij += ( (X[k][i]-X[k][j])*(X[k][i]-X[k][j]) );
                pn = sqrt(xij);//считает длину разности столбцов

                if(norm > pn)
                    norm = pn;//ищет максимальную длину
            }
     return sqrt(norm);
}
//сортировка координат вершин симплекса
void Methods :: Srt(D **X, int N)
{
    int i, j, k;
    D temp;
    D *f = new D[N+1];
    D *box = new D[N];
    D **y = new D*[N+1];
    for(i=0;i<N+1;i++)//динамическая память
        y[i] = new D[N+1];

    for(i=0;i<N;i++)
        box[i] = fit[i];//старые тау в коробку

    for(i=0;i<=N;i++)
    {
        for(j=0;j<N;j++)
            fit[j] = X[j][i];
        f[i] = I();//значения функции в вершинах симплекса
    }

    for(i=0;i<N;i++)
        fit[i] = box[i];//выкладывает тау из коробки

    for(i=0;i<N;i++)
        for(j=0;j<=N;j++)
            y[i][j] = X[i][j];

    for(i=0;i<=N;i++)
        y[N][i] = f[i];//stack(X, f)
//Сортирует столбцы матрицы таким образом,
//чтобы расположить элементы в строке N в порядке возрастания
    for(i=1;i<=N;i++)
        for(j=0;j<=N-i;j++)
            if(y[N][j] >= y[N][j+1])
                for(k=0;k<=N;k++)
                    {
                        temp = y[k][j];
                        y[k][j] = y[k][j+1];
                        y[k][j+1] = temp;
                    }
//submatrix вырезает отсортированное
    for(i=0;i<N;i++)
        for(j=0;j<=N;j++)
            X[i][j] = y[i][j];
/*
    for(i=0;i<=N;i++)
    {
        for(j=0;j<=N;j++)
            cout << y[i][j] << " ";
        cout << endl;
    }
*/
    for(i=0;i<N+1;i++)
        delete[]y[i];
    delete[]box;
    delete[]f;
}

int main()
{
    Methods method;

    //method.ofDescent();
    //method.ofGradient();
    method.ofNelder_Mid();

    return 0;
}

На сегодня достаточно. Следующим этапом будет логично попробовать что-нибудь из глобальной оптимизации, набрать побольше тестовых функций, а затем изучить пакеты со встроенными методами.

Автор: Yermack

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js