Резюме
Приводится описание закономерностей, которые были установлены в последовательном списке всех решений задачи о распределении n-Ферзей. Установлено, что:
- Доля полных решений в общем списке всех решений уменьшается, с ростом значения n.
- Полные решения распределены в последовательном списке всех решений таким образом, что с наибольшей вероятностью встречаются полные решения, расположенные в списке близко друг от друга.
- Существует симметрия в порядке расположения полных решений в общем списке всех решений. Если в i-ой позиции от начала списка решение является полным, то и симметричное решение от конца списка, находящееся в позиции n-i+1 также является полным (правило симметричности решений).
- Любые пары решений, как коротких так и полных, расположенных симметрично в списке всех решений, являются комплементарными – сумма индексов позиций соответствующих строк является постоянной величиной и равна n+1 (правило комплементарности решений). Это говорит о том, что только первая половина списка всех полных решений является «уникальной», любое полное решение из второй половины списка можно получить на основе правила комплементарности. Следствием этого правила является тот факт, что для любого значения n, количество полных решений, всегда будет четным числом.
- Активность ячеек строк матрицы решения симметрична относительно горизонтальной оси, проходящей через середину этой матрицы. Это означает, что активность ячеек i-ой строки всегда совпадает с активностью ячеек строки n-i+1. Под активностью подразумевается частота, с которой встречается индекс ячейки в соответствующей строке списка полных решений. Аналогично, активность ячеек столбцов матрицы решения, симметрична относительно вертикальной оси разделяющей матрицу на две равные части
- Независимо от n, в последовательном поиске всех решений, первое полное решение появляется только после некоторой последовательности коротких решений. Размер начальной последовательности коротких решений увеличивается с ростом n. Длина списка коротких решений до появления первого полного решения для четных значений n значительно больше, чем для ближайших нечетных значений.
- Строка в матрице решений, на которой начинаются затруднения в продвижении вперед, и формируется первое короткое решение, делит матрицу по правилу золотого сечения. Для малых значений n такой вывод является приближенным, однако с ростом значения n точность такого вывода асимптотически возрастает до уровня стандартного правила.
В данной публикации приводятся основные результаты из статьи [1], которая опубликована в журнале «Modeling of Artificial Intelligence, 2018, 5(1)». На Хабре были работы, связанные с проблемой n-Queens:[2], [3],
Задача о распределении n ферзей на шахматной доске размера n x n имеет длинную историю. Первоначально она была сформулирована в 1848 году M. Bezzel [4], как интеллектуальная задача для обычной шахматной доски. Со временем, постановка задачи была расширена F.Nauck [5], и размер шахматной доски мог принимать произвольное значение.
Введение
Формулировка задачи достаточно простая: нужно распределить n ферзей на шахматной доске размера n x n таким образом, чтобы в каждой строке, каждом столбце, а также на левой и правой диагоналях, проходящих через ячейку, где расположен ферзь, не было более одного ферзя. Данную задачу легко понять или объяснить кому либо, но достаточно сложно ее решить. Дело в том, что не существует правил на основе которых можно расположить ферзи в каждой строке так, чтобы получить решение. Решение можно получить только на основе перебора различных вариантов расположения ферзей в тех или иных строках. Однако, сложность такого способа решения состоит в том, что количество всех вариантов расположения ферзей растет экспоненциально с ростом n. Кроме того, выполнение любого шага вперед, для расположения ферзя в свободную позицию некоторой строки, приводит к изменению списка свободных позиций в оставшихся строках, а при возврате назад на один шаг, с целью формирования ветви поиска, необходимо очистить следы ранее выполненных действий.
Имеется большое количество публикаций, связанных с различными аспектами решения проблемы n-Queens. Их можно отнести к нескольким направлениям исследования: поиск всех полных решений для заданного значения размера шахматной доски (n), разработка быстрого алгоритма для нахождения одного решения для различных значений n, решение задачи о комплектации до полного решения, для произвольной композиции из k ферзей, вопросы вычислительной сложности алгоритмических расчетов, а также различные модификации исходной постановки задачи. Для ознакомления с данными направлениями, я бы порекомендовал интересные публикации B. Jordan, S. Brett[6] и I.P. Gent, C. Jefferson, P. Nightingale[7], где приводится достаточно подробный обзор различных направлений исследования. Особо следует отметить интернет-публикацию [8], поддерживаемую Уолтером Костерсом, которая была подготовлена группой из Universiteit Leiden и содержит ссылки на 342 публикации, связанные с проблемой n-queens (по состоянию на декабрь 2018 г).
Хотя проблема n-Queens остается активной более 150 лет, и за это время появилось огромное число публикаций, мне не удалось найти работу, которая имела бы отношение к поиску закономерностей в результатах решения этой задачи. Большинство проектов, связанных с поиском всех решений, скорее всего не сохраняли найденные решения и не смотрели что «там внутри», Там, в постановке задачи были другие доминирующие цели, и наши уважаемые коллеги достигли их. Однако, отдаленно, мне показалось, что ситуация похожа на то, когда человек на завтрак варит яйца, но не ест их, а выбрасывает, оставляя в памяти только количество сваренных яиц. Я всегда был уверен в том, что если данные не случайны, то в них должна быть определенная закономерность, если даже эту закономерность мы не можем найти. Именно такая убежденность была причиной поиска закономерностей в данной задаче.
Наряду с желанием преподнести членам Хабра-сообщества полезную информацию для размышления, я хотел бы, чтобы талантливые программисты, коих на Хабре большинство, обратили бы больше внимания такому направлению развития, как компьютерное моделирование (Computational Simulation). Как метод исследования, такая «Алгоритмическая математика» используется на «переднем крае» многих направлений: Artificial Intelligence, Software Science, Data Science, … и я уверен, что очень сложные и важные для практического применения задачи, будут решены на основе алгоритмической математики и никак иначе.
Определения
Здесь и далее, размер шахматной доски мы будем обозначать символом n. Решение мы будем называть полным, если все n ферзей непротиворечиво расставлены на шахматной доске. Все остальные варианты решения, когда количество правильно расставленных ферзей меньше n – мы будем называть короткими решениями. Под длиной решения мы будем понимать количество (k) правильно расставленных ферзей. Количество всех решений, для данного значения n, будем обозначать символом m. В качестве аналога «шахматной доски» размера n x n., мы будем рассматривать «матрицу решения» размера n x n.
Начало
Для того чтобы провести исследование, был разработан алгоритм поиска всех решений для произвольного значения n. Мы не использовали стандартную рекурсию или обычную систему вложенных циклов. Для больших значений n такой подход был бы достаточно проблематичным. Алгоритм строился на основе совокупности взаимодействующих событий, в каждом из которых, происходит некая система действий, взаимосвязанных между собой. Это дает возможность достаточно просто реализовать механизм изменения пространства состояния при выборе следующего узла в ветви решения задачи (Forward tracking), или же очистки следов ранее выполненных действий, при возврате назад на один или более шагов (Back tracking). В алгоритме нет особых требований к объему памяти или быстродействию процессора.
На основе данного алгоритма были найдены все последовательные решения (как короткие, так и полные) для различных значений матрицы решения n=(7, …, 16). Так как размер списка полных решений является именованной последовательностью The On-Line Encyclopedya of Integer Sequences( последовательность A000170 [9] ) и указан во многих публикациях, мне кажется интересным привести размер списка всех решений (коротких + полных), для рассмотренных нами значений n: 7 (194), 8 (736), 9 (2 936), 10 (12 774), 11 (61 076), 12 (314 730), 13 (1 716 652), 14 (10 030 692), 15 (62 518 772), 16 (415 515 376).
Далее, используя найденные решения, мы приведем формулировки некоторых задач, методы их решения и описание полученных результатов.
1. О пространстве состояний, в котором ведется поиск решений
Перебор различных вариантов расположения ферзей в тех или иных строках матрицы решения размера n, приводит к формированию пространства состояния. Если бы не было никаких запретов по расположению ферзей в те или иные ячейки матрицы, то размер пространства состояния был бы равен nn. Если учитывать только правило, запрещающее расположение более одного ферзя в каждой строке и каждом столбце, то мы получим некоторое подмножество пространства состояния, размер которого будет равен n! Это подмножество пространства состояния соответствует задаче о распределении n ладьей. Если, наряду с этим, учитывать также правило, запрещающее расположение более одного ферзя на левой и правой диагоналях, проходящих через ячейку, где расположен ферзь, то мы получим некоторое пространство поиска, размер которого будет меньше чем n!.. Назовем такое подмножество пространства состояния – продуктивным пространством поиска, исходя из того, что только в этом подпространстве находятся все возможные решения. Любые завершенные ветви в продуктивном пространстве поиска являются решениями с некоторым числом правильно расставленных ферзей. В основном – это короткие решения, и лишь небольшая оставшаяся часть – это полные решения.
На рисунке 1 представлены графики зависимости натурального логарифма трех показателей: a) значения факториала (n!) от размера матрицы решения; b) количества всех решений (как коротких, так и полных); c) количества полных решений — в зависимости от значения размера матрицы решения (n). Как и следовало ожидать, для всех кривых характерен экспоненциальный рост с увеличением значения n. Темпы роста количества всех решений и количества полных решений различаются, хотя на графике это не столь заметно, из-за малого размера выборки значений n. Например, при n=13, разность между логарифмами этих показателей равна 3.148, а при n=16 эта разность увеличивается на величину 0.190 и составляет 3.338. Очевидно, что при дальнейшем увеличении значения n, это расхождение будет более значимым.
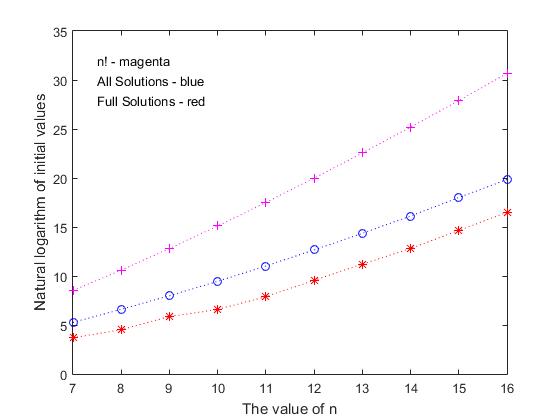
Рис.1 Зависимость логарифма размера пространства состояния от величины n
2. Как изменяется доля полных решений в общем списке всех решений?
Очевидно, что если темп роста количества полных решений отстает от темпов роста количества всех решений, то вероятность нахождения полного решения в общем списке всех решений будет уменьшаться с ростом значения n. На рисунке 2 представлен график зависимости доли полных решений в общем списке всех решений от значения n. Видно, что с увеличением размера матрицы решения, доля всех полных решений в общем списке уменьшается. Для начальных значений n=(7, …, 14), эта величина уменьшается в 5.66 раза от значения 0.2062 до 0.0364, и далее продолжается постепенное, асимптотическое уменьшение этой величины. Здесь возникает формальное противоречие между двумя утверждениями: с одной стороны — количество полных решений экспоненциально растет с ростом значения n, с другой – вероятность получения полного решения в последовательном списке всех решений постоянно уменьшается. Этот, кажущийся парадокс объясняется очень просто, размер продуктивного пространства и связанный с ним размер списка всех решений растет быстрее с увеличением n, чем количество полных решений. Это похоже на попытку найти иголку в стоге сена – количество сена «с увеличением значения n» растет быстрее, чем количество иголок, которые там потерялись. Поэтому, можно предположить, что если для n=27, количество полных решений равно примерно 2.346*1017, то соответствующее значение количества всех решений будет, скорее всего, на 3-4 порядка больше ~ 1020
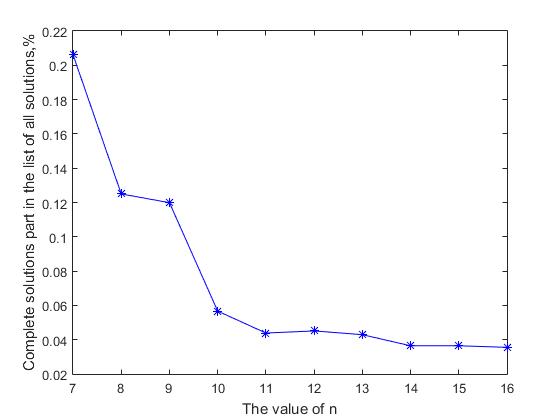
Рис.2 Уменьшение доли полных решений в общем списке всех решений с увеличением значения n
3. Какова частота решений различной длины в списке всех решений?
Как было сказано ранее, все завершенные ветви в продуктивном пространстве поиска являются решениями с различным числом правильно расставленных ферзей.
Для нас представляет интерес, с какой частотой встречаются решения различной длины в общем списке всех решений.
В таблице 1 для значений n=(7,…,12) представлены соответствующие значения относительных частот, для решений, имеющих различную длину. Соответствующее визуальное представление этих данных приведено на рисунке 3.
Анализ таблицы позволяет сделать следующие выводы:
a) для каждой матрицы размера n, существует некоторая длина решения, которая имеет максимальную частоту (выделено жирным).
| nk | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|
| 7 | 10.31 | 31.23 | 27.84 | 20.62 | |||||
| 8 | 2.45 | 20.38 | 34.78 | 29.89 | 12.50 | ||||
| 9 | 0.34 | 5.79 | 21.73 | 35.83 | 34.32 | 11.99 | |||
| 10 | 0.05 | 1.35 | 8.41 | 25.62 | 32.94 | 25.96 | 5.67 | ||
| 11 | 0.15 | 2.12 | 11.80 | 26.71 | 34.47 | 20.36 | 4.39 | ||
| 12 | 0.01 | 0.29 | 3.28 | 13.56 | 29.88 | 31.29 | 17.18 | 4.51 |
b) при увеличении значения n, количество решений с различной длиной увеличивается. Соответственно, при этом уменьшается относительная частота всех решений.
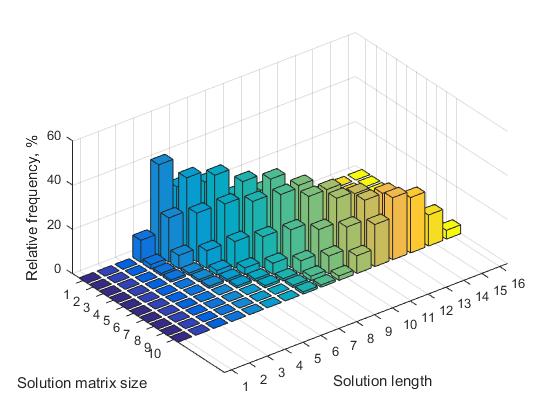
Рис.3 Частота решений различной длины в зависимости от размера матрицы решения, n=7,...,16
c) для каждой матрицы размера n, существует некий минимальный размер длины решения, ниже которого короткие решения не встречаются. С увеличением значения n, величина этого порога увеличивается. Например, для n=8 пороговое значение равно 4, соответственно, при n=16, пороговое значение равно 7.
4. Каким является относительное расположение полных решений в последовательном списке всех решений?
В постановке задачи «о распределении n ферзей» нет причин, которые дали бы основание делать какое-либо предположение о порядке следования полных решений в общем списке всех решений. Нас интересовало, распределены ли полные решения в общем списке равномерно, случайно, или оно имеет какие-то особенности. Чтобы выяснить это, был проведен анализ расстояний между ближайшими полными решениями в последовательном списке всех решений. Как видно из рисунка 4, где для n=12, представлен график изменения соответствующих частот,
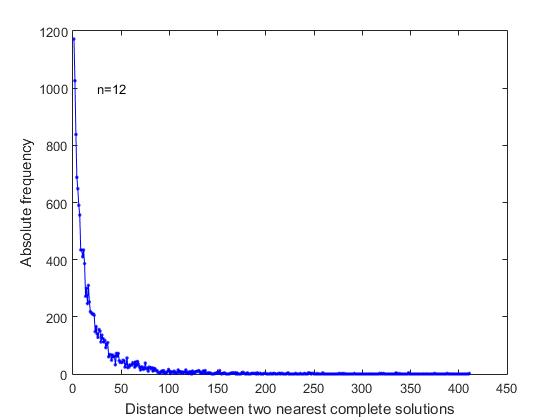
Рис.4 Зависимость частоты от расстояния между ближайшими полными решениями в последовательном списке всех полных решений (n=12)
с наибольшей частотой встречаются полные решения, которые непосредственно следуют друг за другом в общем последовательном списке всех решений. Это те случаи формирования ветви поиска, когда взаимоотношения свободных позиций в последних строках, позволяют формировать два или более, подряд идущих полных решения. Далее, максимальную частоту имеют те полные решения, между которыми расположены: одно короткое решение, два коротких решения и т.д.
5. Существует ли закономерность в расположении полных решений в общем списке всех решений?
Чтобы ответить на этот вопрос, нами были проанализированы последовательные списки всех решений для значений n=(7, …, 16). Чтобы наглядно продемонстрировать полученные результаты, на рисунке 5, для значения n=8, представлен график, где последовательно указана длина каждого решения в списке из всех 736 решений. Здесь только 92 решения являются полными, и они выделены красным цветом, остальные 644 решения являются короткими, и выделены синим цветом. Видно, что полные решения не распределены равномерно в списке всех решений. Есть зоны, где полные решения встречаются чаще, а есть места, где полные решения встречаются редко или вообще не встречаются.
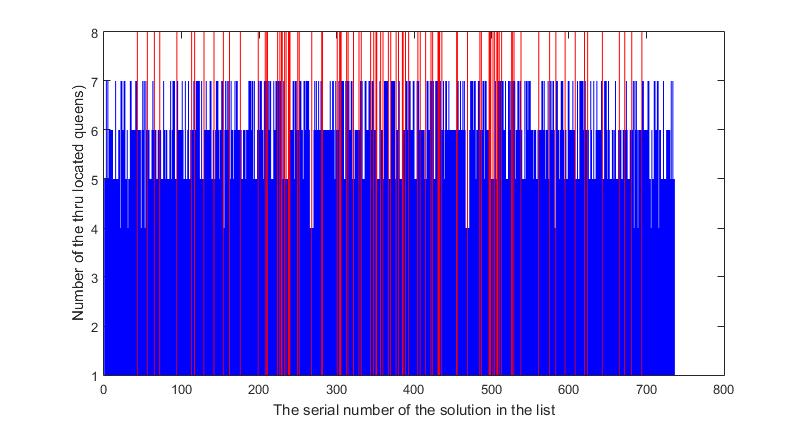
Рис.5 Длина каждого решения в последовательном списке всех решений, для матрицы размера 8 х 8 (red — полные решения, blue – короткие решения). Общее количество всех решений равно 736
Однако, здесь важно другое. Если внимательно посмотреть на рисунок, напоминающий сине-красный штрих-код, то можно заметить одну очень важную особенность, все красные линии симметричны относительно некоторой, условной вертикальной линии, проходящей через середину списка решений. В самом деле, как показывает проверка, если на i-ом шаге от начала общего списка находится полное решение, то соответственно, полное решение обязательно будет обнаружено и на шаге m-i+1. Например, для n=8, если первое полное решение в последовательном поиске всех решений, появляется на 43-ем шаге, то соответственно, последнее полное решение в списке будет обнаружено на шаге 736- 43 +1=694. Если 17-ое решение для матрицы размера 10x10 появляется в списке на 368-ом шаге, то симметричное ему полное решение появится в списке всех решений на шаге 12774-17+1=12407. Это правило справедливо для матрицы решения любого размера. Поэтому мы можем сформулировать правило. Для любого значения n, если в последовательном списке всех решений, в i-ой позиции от начала списка решение является полным, то и симметричное решение от конца списка, находящееся в позиции m-i+1 также будет полным (правило симметричности решений). Здесь m, как указывалось выше, означает количество всех решений. Следствием этого правила является тот факт, что для любого значения n, количество полных решений, всегда будет четным числом. (Все найденные к настоящему времени размеры списка полных решений – являются четными числами).
Если сравнить индексы любых двух симметричных решений, то можно обнаружить принципиально важную особенность – симметричные пары решений являются комплементарными. Сумма соответствующих значений индексов ферзей симметричных решений будет равна n+1. Например, 17-ое решение для n=10 в списке всех решений находится в 368-ом шаге от начала списка и индексы позиций ферзя на этом шаге равны (1, 5, 7, 10, 4, 2, 9, 3, 6, 8).
Соответствующее ему симметричное решение, находится на шаге 12407 и имеет индексы позиций ферзя (10, 6, 4, 1, 7, 9, 2, 8, 5, 3). Если сложить соответствующие значения индексов каждой пары, то получим (11, 11, …,11). Это правило справедливо для любого значения n, причем, как для полных симметричных решений, так и для коротких симметричных решений. Это позволяет нам сформулировать второе правило. Для матрицы решения любого размера n, любые пары решений (как коротких, так и полных), расположенных симметрично в последовательном списке всех решений, являются комплементарными – сумма индексов позиций соответствующих строк является постоянной величиной и равна n+1 (правило комплементарности решений). Если обозначить через Q(i ) и Q1(i) – массивы индексов комплементарных решений, то будет справедливо правило
<b>`Q ( i ) + Q1 ( i ) = n + 1, i = (1, n) `</b>Данное правило означает, что если получено полное решение на i-ом шаге, то тем самым становится известным симметричное полное решение на шаге m – i +1. Поэтому, при поиске всех полных решений, достаточно найти только первую половину всех полных решений. Вторую половину списка полных решений можно будет определить из уже полученных решений, на основе правила комплементарности. Критерием того, что достигнута половина списка полных решений, является выполнение правила комплементарности между предыдущим полным решением Q(i-1) и последующим Q(i) . т.е необходимо, чтобы сумма каждой пары соответствующих значений индексов двух подряд идущих решений была равна n+1. Так как любое полное решение из списка всех полных решений является уникальным, то только те подряд идущие полные решения будут комплементарными, которые находятся по обе стороны от границы, разделяющей список пополам.
Эти два правила позволят в будущем, при поиске всех полных решений для какого-либо очередного значения n, сократить объем вычислений и соответственно время счета в два раза.
6. Визуализация последовательности шагов поиска первого полного решения
Как происходит процесс выполнения шагов вперед(Forward tracking) и возврата назад (Back tracking) при формировании ветви поиска решения? Для того чтобы ответить на этот вопрос, мы, для матрицы размером 10 х 10 определили последовательность из начальных 194 переходов между строками до появления первого полного решения. Соответствующий график представлен на рисунке 6. Голубые линии означают движение вперед, а красные – возврат назад. В течение этих 194 шагов было создано 35 коротких решений. Из рисунка видно, что большая часть переходов (84.5%) происходит между строками (5, 6, 7, 8). Это, своего рода, «узкое место» по пути к «цели». Как следует из рисунка, имеется только 7 случаев перехода на 4-ую строку и один случай перехода на третью строку. Также имеется 13 случаев перехода на 9-ую строку. Три попытки перехода на 10-ую строку оказались безуспешными, так как в этих ветвях поиска на 10-ой строке не оказалось свободной позиции. Данный пример наглядно демонстрирует все ветви формирования коротких
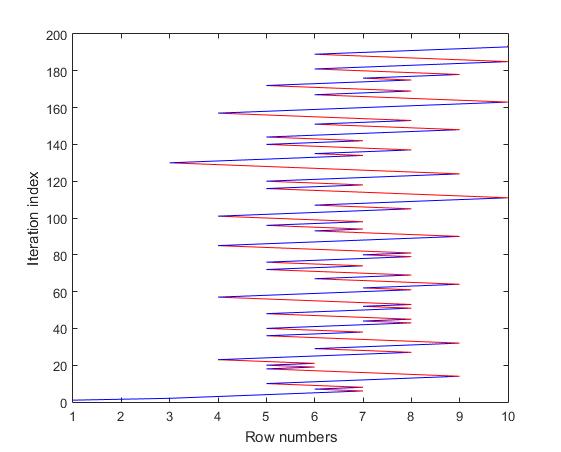
Рис.6 Визуализация событий Backtracking (red) и Forwardtracking (blue) для первых 194 шагов поиска (n=10)
решений, до получения первого полного решения. Любой алгоритм решения подобной задачи будет эффективным, если в ней будет заложен механизм, который позволит исключить все (или часть) ветвей, приводящих к коротким решениям.
7. Через какое количество коротких решений появляется первое полное решение?
Учитывая, что полные решения появляются неодинаково на различных участках списка всех решений, представляется важным выяснить, через какое количество коротких решений появляется первое полное решение при последовательном поиске всех решений. С этой целью, для значений n=(7, … ,35) были последовательно вычислены все короткие решения до появления первого полного решения. Как видно из рисунка 7, где представлен график зависимости от n, натурального логарифма номера шага, когда появилось первое полное решение, для четных значений n первое полное решение появляется значительно позже, чем для ближайших нечетных значений n. Например, для нечетного значения n=21 первое полное решение появляется на шаге 3138, а для следующего, четного значения n=22 первое полное решение появляется на 628169 –ом шаге. Соответственно, для следующего, нечетного значения n=23 первое полное решение появляется на 9155 –ом шаге.
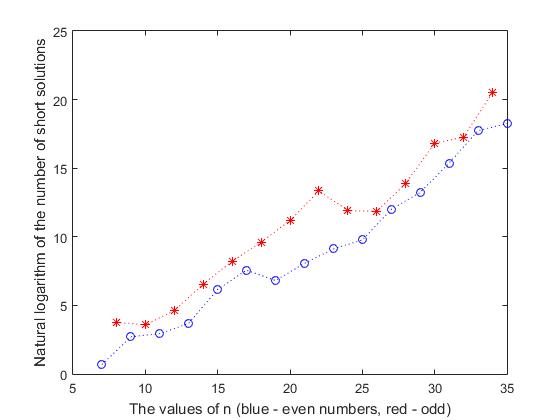
Рис.7 Количество коротких решений до появления первого полного решения, для различных значений n
Количество шагов итерации при четном n=22, соответственно в 200.2 и 68.6 раза больше, чем у ближайших нечетных значений. Особенно наглядно по времени счета это проявляется для n=34. Здесь первое полное решение появляется на 826 337 184-ом шаге, а для ближайших нечетных чисел (33, 35), соответственно на 50 704 900-ом и 84 888 759-ом шагах. Следует также сказать о нарушении монотонности роста числа коротких решений до появления первого полного решения, с ростом n. Для четных значений n это происходит при n=19, для нечетных – при n=24 и n=26.
8. Одинакова ли частота ячеек каждой строки в списке всех полных решений?
Матрица решения размера n x n, которая служит аналогом шахматной доски, это как сцена, на котором происходят все события. Любое полное решение, сформированное на этой сцене, состоит из индексов ячеек различных строк, т.к. каждая такая ячейка является узлом в ветви поиска решения. Вопрос, который нас будет интересовать, состоит в следующем: является ли в каждой строке нагрузка одинаковой для различных ячеек, при формировании списка всех полных решений? Очевидно, что, чем больше значение частоты, тем выше будет активность данной ячейки в формировании списка полных решений. Чтобы установить это, определим для каждой строки на основе списка всех полных решений, относительную частоту различных индексов. Вначале проведем анализ для матрицы решения размером n=8. Рассмотрим последовательно каждую строку массива хранения полных решений и определим частоту различных значений индекса. В таблиц 2, представлены соответствующие значения абсолютных частот активности различных ячеек в каждом из восьми строк, а на рис. 8
| rowcol | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 8 | 16 | 18 | 18 | 16 | 8 | 4 |
| 2 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 3 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 4 | 18 | 8 | 12 | 8 | 8 | 12 | 8 | 18 |
| 5 | 18 | 8 | 12 | 8 | 8 | 12 | 8 | 18 |
| 6 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 7 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 8 | 4 | 8 | 16 | 18 | 18 | 16 | 8 | 4 |
представлена группа из 4 графиков, где каждый график характеризует изменение относительных частот в пределах одной строки. Один из принципиально важных выводов, который можно сделать на основе анализа всех полученных данных состоит в следующем:
- для матрицы решения произвольного размера n, активность ячеек i-ой строки совпадает с активностью ячейки n-i+1, т.е. активность ячеек первой строки всегда совпадает с активностью ячеек последней строки, соответственно, активность ячеек второй строки совпадает с активностью ячеек предпоследней строки и т.д.
В случае, если n нечетно, только медианная строка матрицы решения не имеет симметричной пары, для всех остальных ячеек справедливо указанное выше правило
- Назовем это, «свойством горизонтальной симметрии активности ячеек различных строк матрицы решения». По этой причине мы привели только 4 графика для матрицы решения размера n=8, так как соответствующие графики активности ячеек для строк (1 ,8), (2,7), (3,6) и (4,5) полностью идентичны.
Также следует отметить, что значения частот симметричны относительно вертикальной оси разделяющей матрицу на две равные части (в случае четного значения n), либо проходящей через медианный столбец (в случае нечетного значения n). Назовем это, «свойством вертикальной симметрии активности ячеек различных строк матрицы решения».
Кроме того, как следует из анализа таблицы 2, значения частот в матрице решения симметричны относительно левой и правой главных диагоналей.
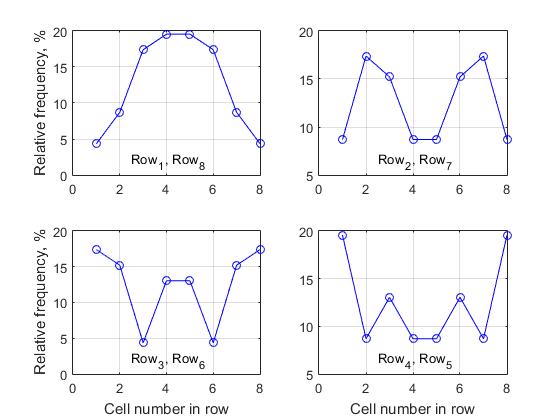
Рис.8 Активность ячеек соответствующих строк при формировании списка полных решений, n=8
Думаю, что наличие ограничивающих правил в постановке задачи, и связанное с этим свойство не детерминированности «формируют» некое гармоничное отношение между узлами в различных строках. Те ветви поиска, которые вписываются в эти правила — приводят к формированию полного решения. Остальные ветви поиска, на каком-то шаге нарушают эти правила, и в итоге, «завершают свой путь» в виде коротких решений. Здесь следует отметить, что ячейки матрицы решения имеют только локальную взаимосвязь в пределах проекционной группы влияния, между ними нет предписанных правил о согласованных действиях. Коллективная активность ячеек – это только следствие от результата воздействия ограничивающих правил. Поэтому, остается открытым достаточно интересный вопрос, каким образом ограничивающие правила, как факторы не детерминированности, воздействуют на ячейки матрицы решения, что это, в итоге приводит к формированию «гармоничной» матрицы активности ячеек – симметричной относительно горизонтальной и вертикальной осей, а также относительно левой и правой главных диагоналей. Является ли это характерным свойством только данной задачи, или оно имеет место и для других не детерминированных задач?
9. С какого номера строки включается алгоритм Forward tracking — Back tracking?
Если проследить за работой алгоритма последовательного выбора строк в матрице решений для расположения ферзя, то можно заметить, что начиная с некоторой строки, которую назовем «StopRow», происходит «торможение» процесса продвижения вперед. В ветви поиска такая строка является первой, где возникают проблемы с наличием свободной
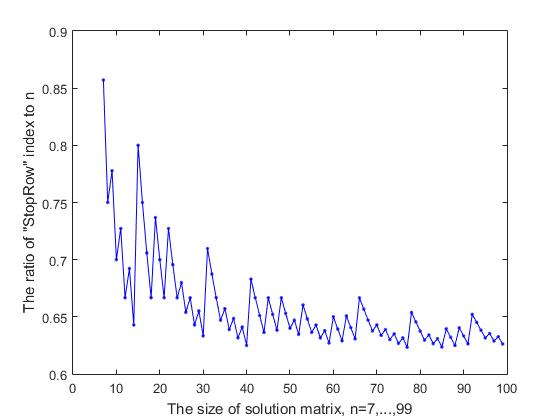
Рис. 9-1 Зависимость отношения индекса StopRow к n от размера матрицы решения (часть-1)
позиции для расположения ферзя. Именно с этой строки включается алгоритм Back tracking для очистки следов ранее выполненных действий, и возврата назад. Это та строка, на которой появляется первое короткое решение.
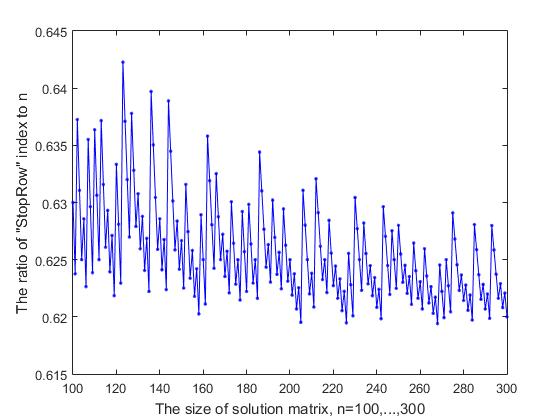
Рис.9-2 Зависимость отношения индекса StopRow к n от размера матрицы решения (часть-2)
Индекс строки «StopRow», с которой начинаются затруднения в продвижении вперед, зависит от размера n матрицы решений. Если рассматривать отношение этого индекса, которую обозначим через StopInd к размеру матрицы решения n, то, как видно из рисунка 9-1, где представлены результаты расчета для начальных значений n=(7, …, 99), это отношение колеблется в большую или меньшую сторону и имеет тенденцию к убыванию. При увеличении значения n= (100, …, 300), это отношение колеблется в пределах 0.619 – 0.642 (рис. 9-2), а при дальнейшем увеличении n, мы получаем следующие результаты (последовательно приводятся значения n, а в скобках – значение StopInd и отношение StopInd/n: 1000(619, 0.6190), 2000(1239, 0.6195), 3000(1856, 0.6187), 4000(2473, 0.6182), 5000(3091, 0.6182). Удивительно, но можно утверждать, что стоп-строка делит матрицу решения по правилу золотого сечения: а именно, отношение StopInd/n отличается от (n-StopInd)/ StopInd на малую величину, которая стремиться к нулю с ростом n. Например, для n=5000 разница между отношениями 3091/5000 и 1909/3091 составляет 0.006, что меньше 0.1% от среднего значения этих двух отношений.
График, представленный на двух рисунках Рис. 9-(1,2) имеет не случайную форму изменчивости, которая напоминает запись на «музыкальном нотном стане». Видны повторяющиеся скачки вверх и ступенчатое падение вниз с некоторой нерегулярной периодичностью. Очевидно, что есть некая причина, обусловливающая такой характер поведения кривой, и возможно, это представит интерес для исследования. По этой причине, с целью более подробной визуализации, график был представлен на двух рисунках.
Я рассмотрел только часть вопросов, которые можно сформулировать на основе результатов решения задачи «о распределении n-ферзей». Надеюсь, что полученные результаты сделают более прозрачными для понимания механизмы формирования не детерминированных процессов и изменения пространства состояния. Возможно, это послужит точкой опоры для формулировки новых задач и продвижения вперед.
Заключение
- Если, просматривая публикацию, дошли до заключения, то естественно, возникнет вопрос: «а при чем тут One Billion Queens Problem Solution в заголовке статьи?». Подготавливая публикацию для Хабра, я подумал, что человек, который обладает, к примеру, рудником, где добывают алмазы, должен подарить хотя бы по одному алмазу своим друзьям и близким, иначе это было бы несправедливо. Поэтому, я хотел бы преподнести подарок всем членам хабра-сообщества: участникам, организаторам, посетителям. Как следует из названия, это решение задачи о распределении одного миллиарда ферзей на шахматной доске размера миллиард на миллиард.
Конечно, это не алмаз граненный, но для настоящих ценителей интеллектуального искусства, это может быть более ценным, чем «какой-то там алмаз». Тем более алмазов много разных по миру, а это решение пока только в одном экземпляре. И видит наш Byte-Бог (*), что делаю я это искренне.
Полученное решение — это одномерный массив, состоящий из одного миллиарда чисел, который представлен в формате MatLab .mat и доступен по адресу:One Billion Queens Problem Solution на Google Drive
-Первый элемент этого массива характеризует позицию ферзя в первой строке, второй элемент – позицию во второй строке и т.д. Это только одно решение из nBillion возможных решений. А значение nBillion это настолько большое число, что его можно считать близким родственником бесконечности. - Мне кажется, что данное решение можно отнести к категории виртуальных интеллектуальных ценностей. Можно сказать, что «это нечто, в котором что-то есть». Их реально «потрогать» не получится, так что оно воспринимается в сознании только на уровне ощущений. Там, в самом деле, есть удивительный порядок и явная и неявная гармония. Это, чисто символический подарок (в прямом и переносном смысле), который адресован всем членам сообщества. Я думаю, что «Вы не такие как все».
(Надеюсь, что кто-то «заберет подарок домой». Файл достаточно большой – 3.7 Gb. Это чистые, проверенные данные. То, что Google Drive выведет предупреждения – отнеситесь к этому с пониманием)
- Прежде чем принять данное решение я подумал об индивидуально-коллективном характере такого подарка. Не получится ли так, что одному будет вручен оригинал, а остальным копии? Но решение оказалось простым. Привычные нам «житейские» понятия «оригинал» и «копия» в данном случае, теряют смысл. Мы не копируем, а создаем еще один оригинал. А «оригиналы» для всех одинаковы и равно эквивалентны.
- Думаю, что в компании родственников, вы, скорее всего, будете единственным, кто получил в подарок такое «интеллектуальное изделие». Будет весело, если вы расскажете тёще о таком подарке: «Представьте себе мамо шахматную доску размером 50 000 км на 50 000 км, на которой распределены 1 миллиард ферзей таким образом, что один другого в упор не видит…». Кто знает, может после этого, будут больше ценить зятя, раз ему такой странный подарок вручают.
Желаю всем членам хабра-сообщества здоровья, успехов и благополучия. Пусть новый год принесет всем нам удачу.
(*) – Раз уж сослался на имя объекта, то следует привести и его описание.
Под Byte-Богом подразумевается многомерная сущность, состоящая из нулей и единиц, разумная во всех смыслах и бесконечная по всем направлениям. Любая последовательность из нулей и единиц в этом пространстве представляет определенные знания.
Список литературы
[4] Max Bezzel, Proposal of 8-queens problem", Berliner Schachzeitung, Volume
3 (1848), page 363. (Submitted under the author name Schachfreund".)
[5] Franz Nauck, Briefwechseln mit allen fur alle", Illustrirte Zeitung, Volume
377 Number 15 (1850), page 182.
[6 ] Bell Jordan; Stevens Brett (2009). "A survey of known results and research areas for n-queens". Discrete Mathematics. 309 (1): 1–31
[7] Gent, Ian P.; Jefferson, Christopher; Nightingale, Peter (August 2017). "Complexity of n-Queens Completion". Journal of Artificial Intelligence Research. AAAI Press. 59: 815–848
[8] W. Kosters and all, n-Queens — 342 references, (November 20, 2018)
[9] N.J.A. Sloane, the On-Line Encyclopedia of Integer Sequences, published electronically. 2016
Автор: ericgrig






