Функциональное мышление. Часть 6

Продолжаем нашу серию статей о функциональном программировании на F#. Сегодня расскажем об ассоциативности и композиции функций, а также сравним композицию и конвейер. Заглядывайте под кат!

• Первая часть
• Вторая часть
• Третья часть
• Четвертая часть
• Пятая часть

Ассоциативность и композиция функций

Ассоциативность функций

Пусть, есть цепочка функций написанных в ряд. В каком порядке они будут скомбинированы?

Например, что значит эта функция?

let F x y z = x y z

Значит ли это, что функция y должна быть применена к аргументу z, а затем полученный результат должен быть передан в x? Т.е.:

let F x y z = x (y z)

Или функция x применяется к аргументу y, после чего функция, полученная в результате, будет вычислена с аргументом z? Т.е.:

let F x y z = (x y) z

1. Верен второй вариант.
2. Применение функций имеет левую ассоциативность.
3. x y z значит тоже самое что и (x y) z.
4. А w x y z равно ((w x) y) z.
5. Это не должно выглядеть удивительным.
6. Мы уже видели как работает частичное применение.
7. Если рассуждать об x как о функции с двумя параметрами, то (x y) z — это результат частичного применения первого параметра, за которым следует передача аргумента z к промежуточной функции.

Если нужна правая ассоциативность, можно использовать скобки или pipe. Следующие три записи эквивалентны:

let F x y z = x (y z)
let F x y z = y z |> x    // использование прямого конвейера
let F x y z = x <| y z    // использование обратного конвейера

В качестве упражнения, попробуйте вывести сигнатуры этих функций без реального вычисления.

Композиция функций

Мы упоминали композицию функций несколько раз, но что в действительности означает данный термин? Он кажется устрашающим на первый взгляд, но на самом деле все довольно просто.

Скажем, у нас есть функция "f", которая сопоставляет тип "T1" к типу "T2". Также у нас есть функция "g", которая преобразует тип "T2" в тип "T3". Тогда мы можем соединить вывод "f" и ввод "g", создав новую функцию, которая преобразует тип "T1" к типу "T3".

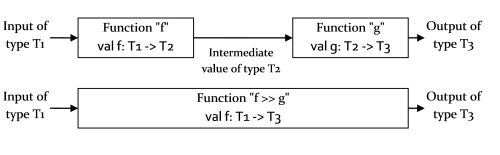
Например:

let f (x:int) = float x * 3.0  // f это ф-ция типа int->float
let g (x:float) = x > 4.0      // g это ф-ция типа float->bool

Мы можем создать новую функцию "h", которая берет вывод "f" и использует его в качестве ввода для "g".

let h (x:int) =
    let y = f(x)
    g(y)                   // возвращаем результат вызова g

Чуть более компактно:

let h (x:int) = g ( f(x) ) // h это функция типа int->bool

//тест
h 1
h 2

Так далеко, так просто. Это интересно, мы можем определить новую функцию "compose", которая принимает функции "f" и "g" и комбинирует их даже не зная их сигнатуры.

let compose f g x = g ( f(x) )

После выполнения можно увидеть, что компилятор правильно решил, что "f" — это функция обобщенного типа 'a к обобщенному типу 'b, а "g" ограничена вводом типа 'b:

val compose : ('a -> 'b) -> ('b -> 'c) -> 'a -> 'c

(Обратите внимание, что обобщенная композиция операций возможна только благодаря тому, что каждая функция имеет ровно один входной параметр и один вывод. Данный подход невозможен в нефункциональных языках.)

Как мы видим, данное определение используется для оператора ">>".

let (>>) f g x = g ( f(x) )

Благодаря данному определению можно строить новые функции на основе существующих при помощи композиции.

let add1 x = x + 1
let times2 x = x * 2
let add1Times2 x = (>>) add1 times2 x

//тест
add1Times2 3

Явная запись весьма громоздка. Но можно сделать ее использование более простым для понимания.

Во первых, можно избавиться от параметра x, и композиция вернет частичное применение.

let add1Times2 = (>>) add1 times2

Во вторых, т.к. >> является бинарным оператором, можно поместить его в центре.

let add1Times2 = add1 >> times2

Применение композиции делает код чище и понятнее.

let add1 x = x + 1
let times2 x = x * 2

// по старому
let add1Times2 x = times2(add1 x)

// по новому
let add1Times2 = add1 >> times2

Использование оператора композиции на практике

Оператор композиции (как и все инфиксные операторы) имеет более низкий приоритет, чем обычные функции. Это означает, что функции использованные в композиции могут иметь аргументы без использования скобок.

Например, если у функций "add" и "times" есть параметры, они могут быть переданы во время композиции.

let add n x = x + n
let times n x = x * n
let add1Times2 = add 1 >> times 2
let add5Times3 = add 5 >> times 3

//тест
add5Times3 1

Пока соответствующие входы и выходы функций совпадают, функции могут использовать любые значения. Например, рассмотрим следующий код, который выполняет функцию дважды:

let twice f = f >> f    //сигнатура ('a -> 'a) -> ('a -> 'a)

Обратите внимание, что компилятор вывел, что "f" принимает и возвращает значения одного типа.

Теперь рассмотрим функцию "+". Как мы видели ранее, ввод является int-ом, но вывод в действительности — (int->int). Таким образом "+" может быть использована в "twice". Поэтому можно написать:

let add1 = (+) 1           // сигнатура (int -> int)
let add1Twice = twice add1 // сигнатура так же (int -> int)

//тест
add1Twice 9

С другой стороны нельзя написать:

let addThenMultiply = (+) >> (*)

Потому что ввод "*" должен быть int, а не int->int функцией (который является выходом сложения).

Но если подправить первую функцию так, чтобы она возвращала только int, все заработает:

let add1ThenMultiply = (+) 1 >> (*) 
// (+) 1 с сигнатурой (int -> int) и результатом 'int'

//тест
add1ThenMultiply 2 7

Композиция также может быть выполнена в обратном порядке посредством "<<", если это необходимо:

let times2Add1 = add 1 << times 2
times2Add1 3

Обратная композиция в основном используется для того, чтобы сделать код более похожим на английский язык ("English-like"). Например:

let myList = []
myList |> List.isEmpty |> not    // прямой конвейер

myList |> (not << List.isEmpty)  // использование обратной композиции

Композиция vs. конвейер

Вы можете быть сбиты с толку небольшой разницей между композицией и конвейером, т.к. они могут выглядеть очень похожими.

Во первых, посмотрите на определение конвейера:

let (|>) x f = f x

Все это позволяет поставить аргументы функций перед ней, а не после. Вот и все. Если у функции есть несколько параметров, то ввод должен быть последним параметром (в текущем наборе параметров, а не вообще). Пример, встречаемый ранее:

let doSomething x y z = x+y+z
doSomething 1 2 3       // все параметры указаны после функции
3 |> doSomething 1 2    // последний параметр конвейеризирован в функцию

Композиция не тоже самое и не может быть заменой пайпу. В следующем примере даже число 3 не функция, поэтому "вывод" не может быть передан в doSomething:

3 >> doSomething 1 2     // ошибка
// f >> g  то же самое что и  g(f(x)) так что можем переписать это:
doSomething 1 2 ( 3(x) ) // подразумевается что 3 должно быть функцией!
// error FS0001: This expression was expected to have type 'a->'b
//               but here has type int

Компилятор жалуется, что значение "3" должно быть разновидностью функций 'a->'b.

Сравните это с определением композиции, которая берет 3 аргумента, где первые два должны быть функциями.

let (>>) f g x = g ( f(x) )

let add n x = x + n
let times n x = x * n
let add1Times2 = add 1 >> times 2

Попытки использовать конвейер вместо композиции обернутся ошибкой компиляции. В следующем примере "add 1" — это (частичная) функция int->int, которая не может быть использована в качестве второго параметра для "times 2".

let add1Times2 = add 1 |> times 2   //  ошибка
// x |> f то же самое что и  f(x) так что можем переписать это:
let add1Times2 = times 2 (add 1)    // add1 должно быть 'int'
// error FS0001: Type mismatch. 'int -> int' does not match 'int'

Компилятор пожалуется, что "times 2" необходимо принимать параметр int->int, т.е. быть функцией (int->int)->'a.

Дополнительные ресурсы

Для F# существует множество самоучителей, включая материалы для тех, кто пришел с опытом C# или Java. Следующие ссылки могут быть полезными по мере того, как вы будете глубже изучать F#:

• F# Guide
• F# for Fun and Profit
• F# Wiki
• Learn X in Y Minutes: F#

Также описаны еще несколько способов, как начать изучение F#.

И наконец, сообщество F# очень дружелюбно к начинающим. Есть очень активный чат в Slack, поддерживаемый F# Software Foundation, с комнатами для начинающих, к которым вы можете свободно присоединиться. Мы настоятельно рекомендуем вам это сделать!

Не забудьте посетить сайт русскоязычного сообщества F#! Если у вас возникнут вопросы по изучению языка, мы будем рады обсудить их в чатах:

• комната #ru_general в Slack-чате F# Software Foundation
• чат в Telegram
• чат в Gitter
• комната #ru_general в Slack-чате F# Software Foundation

Об авторах перевода

Автор перевода @kleidemos
Перевод и редакторские правки сделаны усилиями русскоязычного сообщества F#-разработчиков. Мы также благодарим @schvepsss и @shwars за подготовку данной статьи к публикации.

Автор: shwars

Источник