Итак, очередная статья из цикла «математика на пальцах». Сегодня мы продолжим разговор о методах наименьших квадратов, но на сей раз с точки зрения программиста. Это очередная статья в серии, но она стоит особняком, так как вообще не требует никаких знаний математики. Статья задумывалась как введение в теорию, поэтому из базовых навыков она требует умения включить компьютер и написать пять строк кода. Разумеется, на этой статье я не остановлюсь, и в ближайшее же время опубликую продолжение. Если сумею найти достаточно времени, то напишу книгу из этого материала. Целевая публика — программисты, так что хабр подходящее место для обкатки. Я в целом не люблю писать формулы, и я очень люблю учиться на примерах, мне кажется, что это очень важно — не просто смотреть на закорючки на школьной доске, но всё пробовать на зуб.
Итак, начнём. Давайте представим, что у меня есть триангулированная поверхность со сканом моего лица (на картинке слева). Что мне нужно сделать, чтобы усилить характерные черты, превратив эту поверхность в гротескную маску?
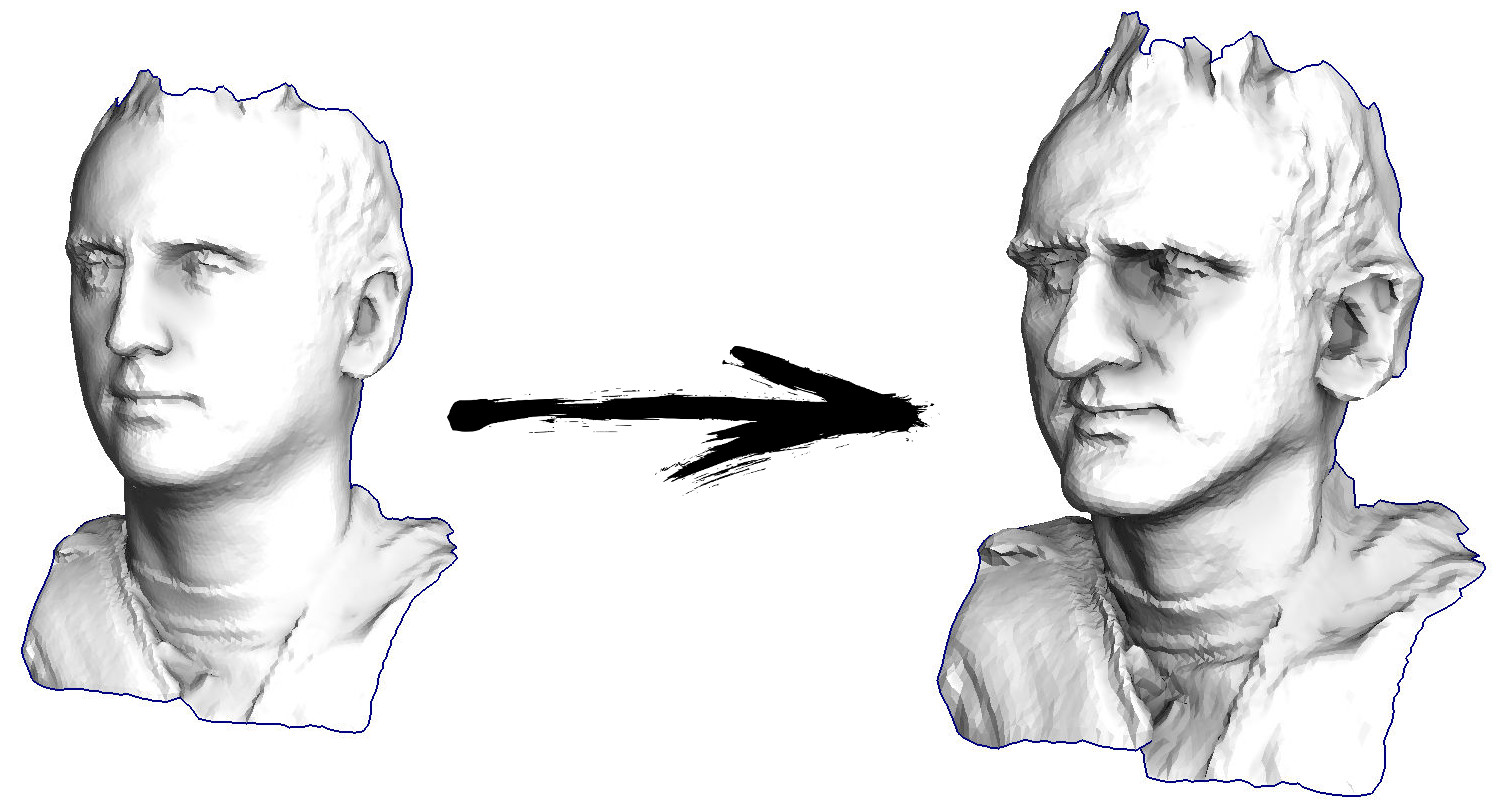
В данном конкретном случае я решаю эллиптическое дифференциальное уравнение, носящее имя Симеона Деми Пуассона. Товарищи программисты, давайте сыграем в игру: прикиньте, сколько строк в C++ коде, его решающем? Сторонние библиотеки вызывать нельзя, у нас в распоряжении только голый компилятор. Ответ под катом.
На самом деле, двадцати строк кода достаточно для солвера. Если считать со всем-всем, включая парсер файла 3Д модели, то в двести строк уложиться — раз плюнуть.
Пример 1: сглаживание данных
Давайте расскажу, как это работает. Начнём издалека, представьте, что у нас есть обычный массив f, например, из 32 элементов, инициализированный следующим образом:
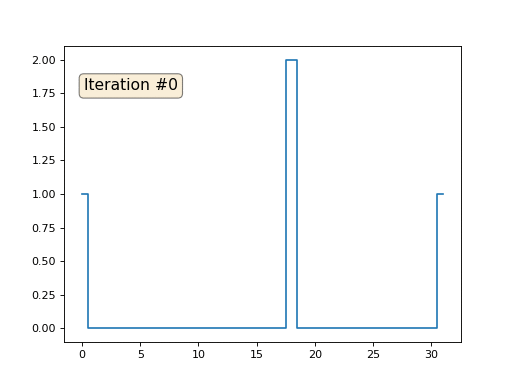
А затем мы тысячу раз выполним следующую процедуру: для каждой ячейки f[i] мы запишем в неё значение среднее значение соседних ячеек: f[i] = ( f[i-1] + f[i+1] )/2. Чтобы было понятнее, вот полный код:
import matplotlib.pyplot as plt
f = [0.] * 32
f[0] = f[-1] = 1.
f[18] = 2.
plt.plot(f, drawstyle='steps-mid')
for iter in range(1000):
f[0] = f[1]
for i in range(1, len(f)-1):
f[i] = (f[i-1]+f[i+1])/2.
f[-1] = f[-2]
plt.plot(f, drawstyle='steps-mid')
plt.show()
Каждая итерация будет сглаживать данные нашего массива, и через тысячу итераций мы получим постоянное значение во всех ячейках. Вот анимация первых ста пятидесяти итераций:
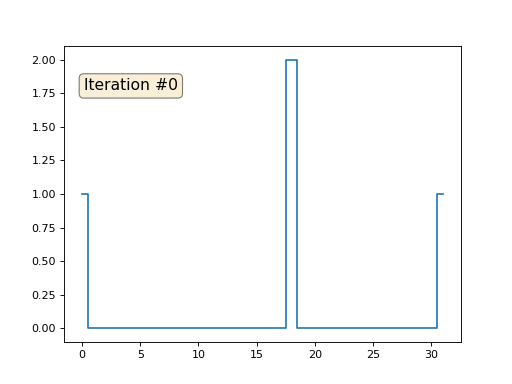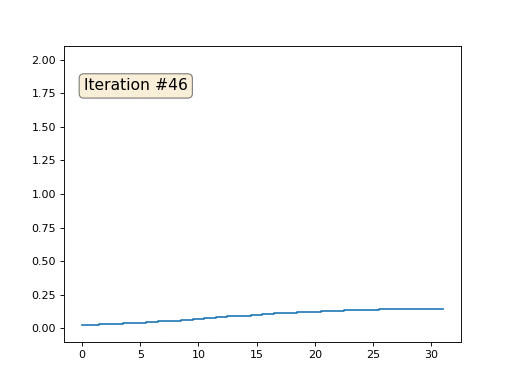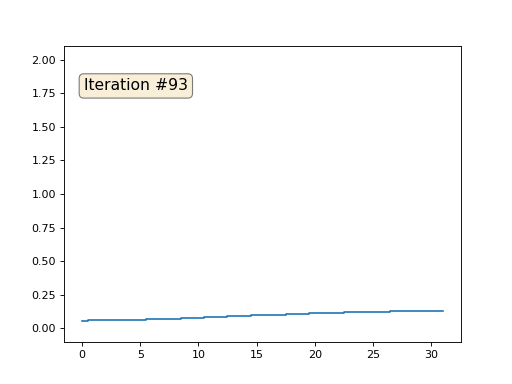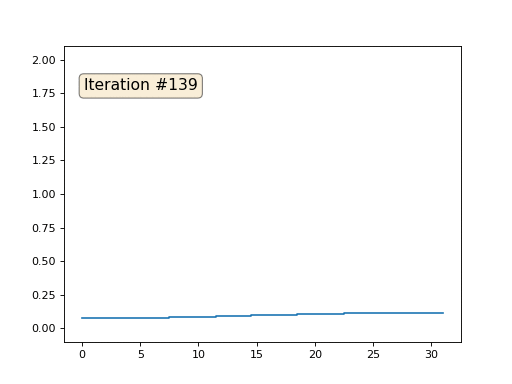
Если вам неясно, почему происходит сглаживание, прямо сейчас остановитесь, возьмите ручку и попробуйте порисовать примеры, иначе дальше читать не имеет смысла. Триангулированная поверхность ничем принципиально от этого примера не отличается. Представьте, что для каждой вершины мы найдём соседние с ней, посчитаем их центр масс, и передвинем нашу вершину в этот центр масс, и так десять раз. Результат будет вот таким:
Разумеется, если не остановиться на десяти итерациях, то через некоторое время вся поверхность сожмётся в одну точку ровно так же, как и в предыдущем примере весь массив стал заполнен одним и тем же значением.
Пример 2: усиление/ослабление характеристических черт
Полный код доступен на гитхабе, а здесь я приведу самую важную часть, опустив лишь чтение и запись 3Д моделей. Итак, триангулированная модель у меня представлена двумя массивами: verts и faces. Массив verts — это просто набор трёхмерных точек, они же вершины полигональной сетки. Массив faces — это набор треугольников (количество треугольников равно faces.size()), для каждого треугольника в массиве хранятся индексы из массива вершин. Формат данных и работу с ним я подробно описывал в своём курсе лекций по компьютерной графике. Есть ещё третий массив, который я пересчитываю из первых двух (точнее, только из массива faces) — vvadj. Это массив, который для каждой вершины (первый индекс двумерного массива) хранит индексы соседних с ней вершин (второй индекс).
std::vector<Vec3f> verts;
std::vector<std::vector<int> > faces;
std::vector<std::vector<int> > vvadj;
Первое, что я делаю, это для каждой вершины моей поверхности считаю вектор кривизны. Давайте проиллюстрируем: для текущей вершины v я перебираю всех её соседей n1-n4; затем я считаю их центр масс b = (n1+n2+n3+n4)/4. Ну и финальный вектор кривизны может быть посчитан как c=v-b, это не что иное, как обычные конечные разности для второй производной.
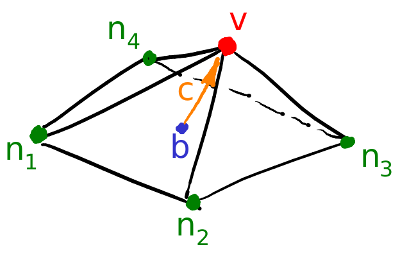
Непосредственно в коде это выглядит следующим образом:
std::vector<Vec3f> curvature(verts.size(), Vec3f(0,0,0));
for (int i=0; i<(int)verts.size(); i++) {
for (int j=0; j<(int)vvadj[i].size(); j++) {
curvature[i] = curvature[i] - verts[vvadj[i][j]];
}
curvature[i] = verts[i] + curvature[i] / (float)vvadj[i].size();
}
Ну а дальше мы много раз делаем следующую вещь (смотрите предыдущую картинку): мы вершину v двигаем v := b + const * c. Обратите внимание, что если константа равна единице, то наша вершина никуда не сдвинется! Если константа равна нулю, то вершина заменяется на центр масс соседних вершин, что будет сглаживать нашу поверхность. Если константа больше единицы (заглавная картинка сделана при помощи const=2.1), то вершина будет сдвигаться в направлении вектора кривизны поверхности, усиливая детали. Вот так это выглядит в коде:
for (int it=0; it<100; it++) {
for (int i=0; i<(int)verts.size(); i++) {
Vec3f bary(0,0,0);
for (int j=0; j<(int)vvadj[i].size(); j++) {
bary = bary + verts[vvadj[i][j]];
}
bary = bary / (float)vvadj[i].size();
verts[i] = bary + curvature[i]*2.1; // play with the coeff here
}
}
Кстати, если меньше единицы, то детали будут наоборот ослабляться (const=0.5), но это не будет эквивалентно простому сглаживанию, «контраст картинки» останется:
Обратите внимание, что мой код генерирует файл 3Д модели в формате Wavefront .obj, рендерил я в сторонней программе. Посмотреть получившуюся модель можно, например, в онлайн-вьюере. Если вам интересны именно методы отрисовки, а не генерирование модели, то читайте мой курс лекций по компьютерной графике.
Пример 3: добавляем ограничения
Давайте вернёмся к самому первому примеру, и сделаем ровно то же самое, но только не будем переписывать элементы массива под номерами 0, 18 и 31:
import matplotlib.pyplot as plt
x = [0.] * 32
x[0] = x[31] = 1.
x[18] = 2.
plt.plot(x, drawstyle='steps-mid')
for iter in range(1000):
for i in range(len(x)):
if i in [0,18,31]: continue
x[i] = (x[i-1]+x[i+1])/2.
plt.plot(x, drawstyle='steps-mid')
plt.show()
Остальные, «свободные» элементы массива я инициализировал нулями, и по-прежнему итеративно заменяю их на среднее значение соседних элементов. Вот так выглядит эволюция массива на первых ста пятидесяти итерациях:
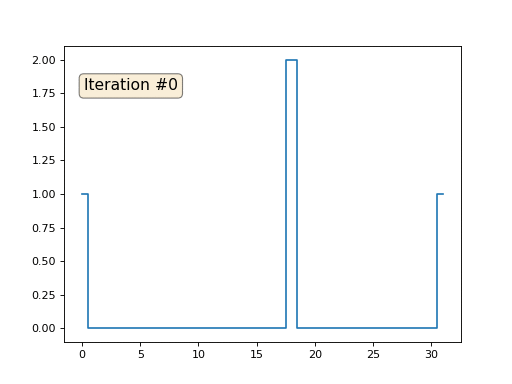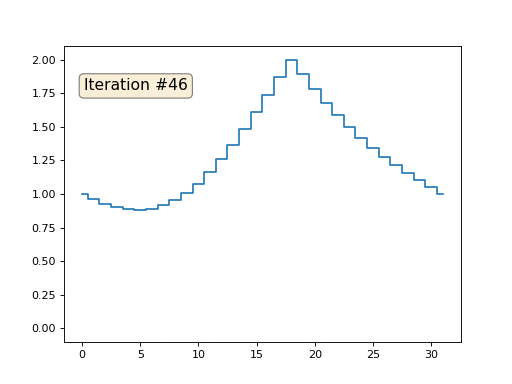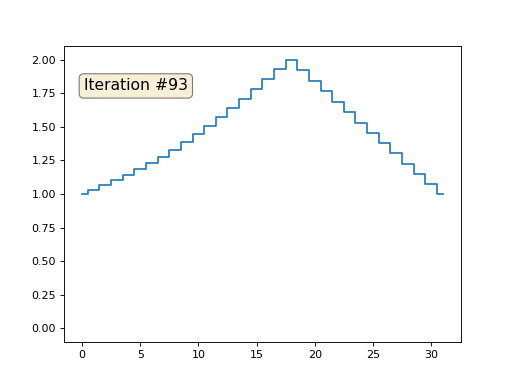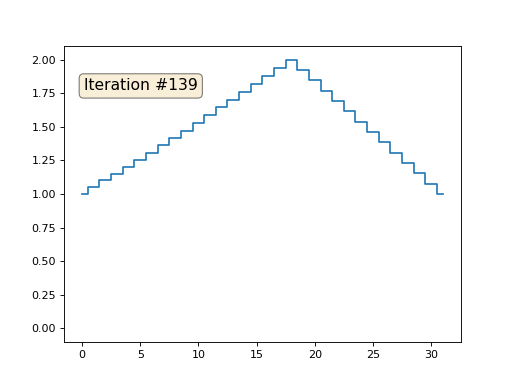
Вполне очевидно, что на сей раз решение сойдётся не к постоянному элементу, заполняющему массив, а к двум линейным рампам. Кстати, действительно ли всем очевидно? Если нет, то экспериментируйте с этим кодом, я специально привожу примеры с очень коротким кодом, чтобы можно было досконально разобраться с происходящим.
Лирическое отступление: численное решение систем линейных уравнений.
Пусть нам дана обычная система линейных уравнений:
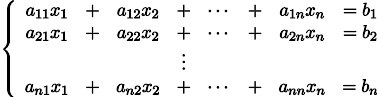
Её можно переписать, оставив в каждом из уравнений с одной стороны знака равенства x_i:
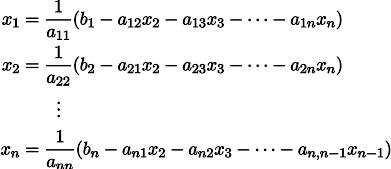
Пусть нам дан произвольный вектор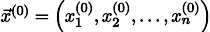 
, приближающий решение системы уравнений (например, нулевой).
Тогда, воткнув его в правую часть нашей системы, мы можем получить обновлённый вектор приближения решения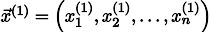 
.
Чтобы было понятнее, x1 получается из x0 следующим образом:
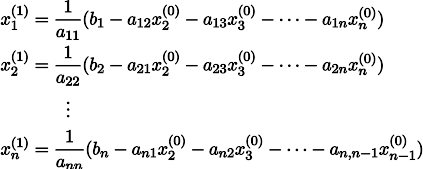
Повторив процесс k раз, решение будет приближено вектором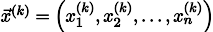 
Давайте на всякий случай запишем рекурретную формулу:
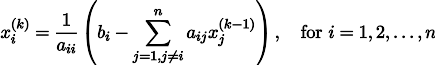
При некоторых предположениях о коэффициентах системы (например, вполне очевидно, что диагональные элементы не должны быть нулевыми, т.к. мы на них делим), данная процедура сходится к истинному решению. Эта гимнастика известна в литературе под названием метода Якоби.
Пример 3 ещё раз, но уже с другой стороны
А теперь давайте ещё раз внимательно посмотрим на основной цикл из примера 3:
for iter in range(1000):
for i in range(len(x)):
if i in [0,18,31]: continue
x[i] = (x[i-1]+x[i+1])/2.
Я стартовал с какого-то начального вектора x, и тысячу раз его обновляю, причём процедура обновления подозрительно похожа на метод Якоби! Давайте выпишем эту систему уравнений в явном виде:
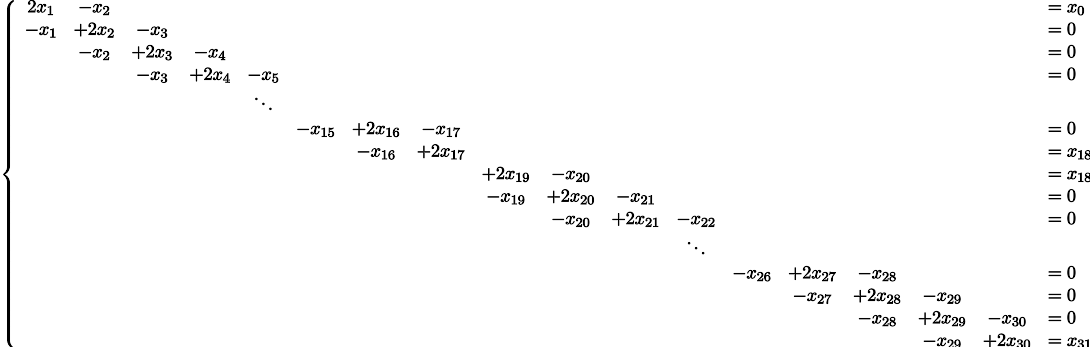
Потратьте немного времени, убедитесь, что каждая итерация в моём питоновском коде — это строго одно обновление метода Якоби для этой системы уравнений. Значения x[0], x[18] и x[31] у меня зафиксированы, соответственно, в набор переменных они не входят, поэтому они перенесены в правую часть.
Итого, все уравнения в нашей системе выглядят как — x[i-1] + 2 x[i] — x[i+1] = 0. Это выражение не что иное, как обычные конечные разности для второй производной. То есть, наша система уравнений нам просто-напросто предписывает, что вторая производная должна быть везде равна нулю (ну, кроме как в точке x[18]). Помните, я говорил, что вполне очевидно, что итерации должны сойтись к линейным рампам? Так именно поэтому, у линейной функции вторая производная нулевая.
А вы знаете, что мы с вами только что решили задачу Дирихле для уравнения Лапласа?
Кстати, внимательный читатель должен был бы заметить, что, строго говоря, у меня в коде системы линейных уравнений решаются не методом Якоби, но методом Гаусса-Зейделя, который является своебразной оптимизацией метода Якоби:
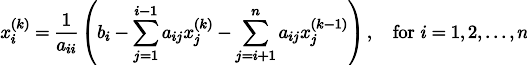
Пример 4: уравнение Пуассона
А давайте мы самую малость изменим третий пример: каждая ячейка помещается не просто в центр масс соседних ячеек, но в центр масс плюс некая (произвольная) константа:
import matplotlib.pyplot as plt
x = [0.] * 32
x[0] = x[31] = 1.
x[18] = 2.
plt.plot(x, drawstyle='steps-mid')
for iter in range(1000):
for i in range(len(x)):
if i in [0,18,31]: continue
x[i] = (x[i-1]+x[i+1] +11./32**2 )/2.
plt.plot(x, drawstyle='steps-mid')
plt.show()
В прошлом примере мы выяснили, что помещение в центр масс — это дискретизация оператора Лапласа (в нашем случае второй производной). То есть, теперь мы решаем систему уравнений, которая говорит, что наш сигнал должен иметь некую постоянную вторую производную. Вторая производная — это кривизна поверхности; таким образом, решением нашей системы должна стать кусочно-квадратичная функция. Проверим на дискретизации в 32 сэмпла:
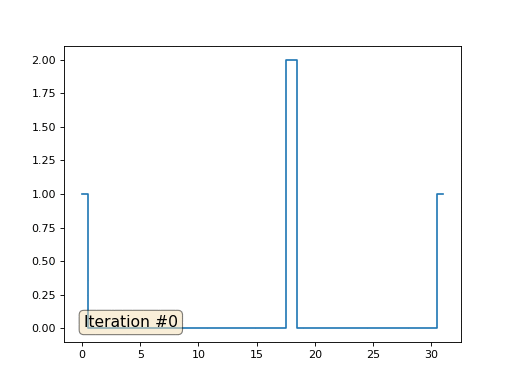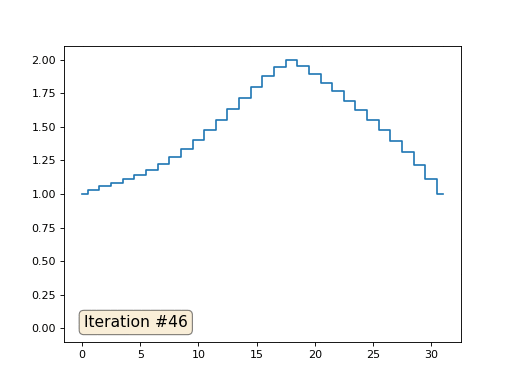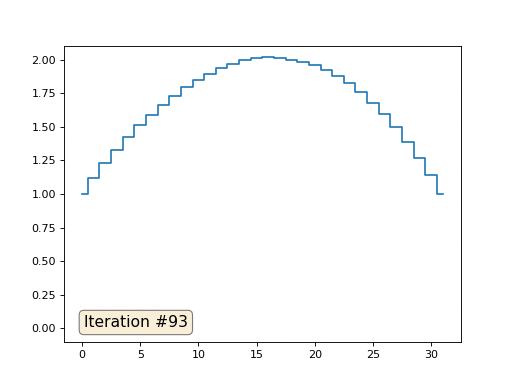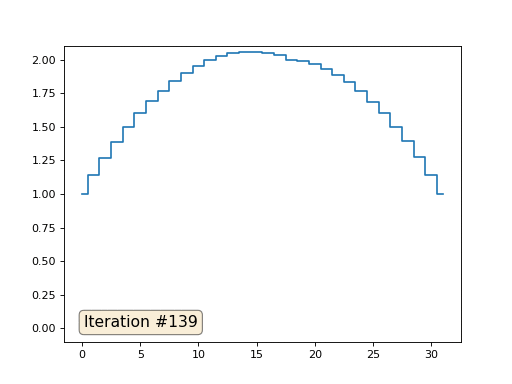
При длине массива в 32 элемента наша система сходится к решению за пару сотен итераций. А что будет, если мы попробуем массив в 128 элементов? Тут всё гораздо печальнее, количество итераций нужно уже исчислять тысячами:
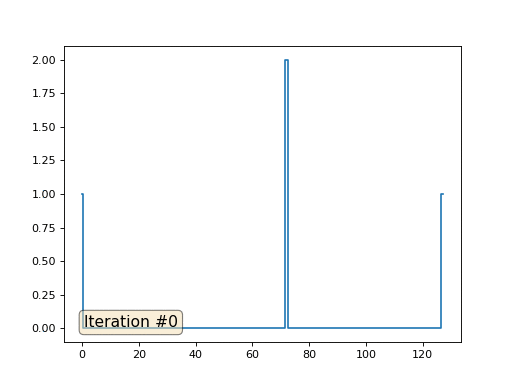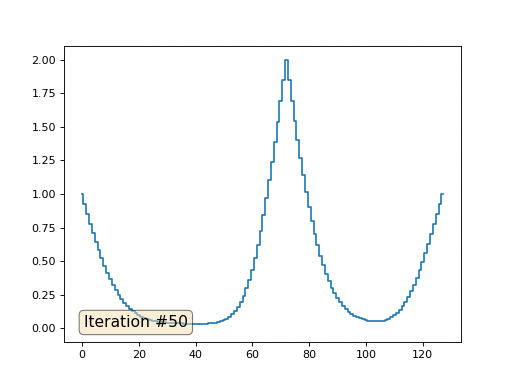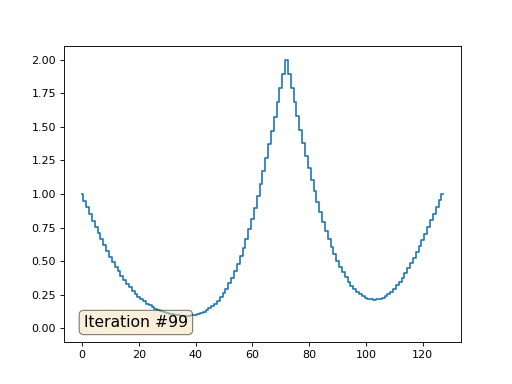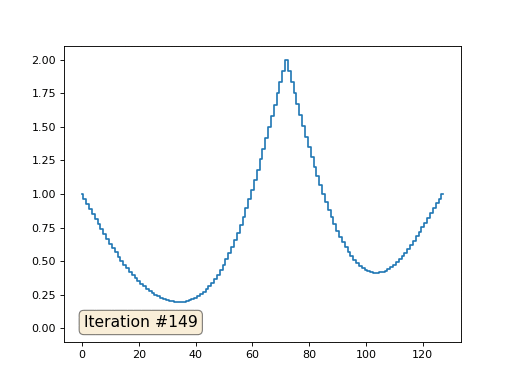
Метод Гаусса-Зейделя крайне прост в программировании, но малоприменим для больших систем уравнений. Можно попытаться его ускорить, применяя, например, многосеточные методы. На словах это может звучать громоздко, но идея крайне примитивная: если мы хотим решение с разрешением в тысячу элементов, то можно для начала решить с десятью элементами, получив грубую аппроксимацию, затем удвоить разрешение, решить ещё раз, и так далее, пока не достигнем нужного результата. На практике это выглядит следующим образом:
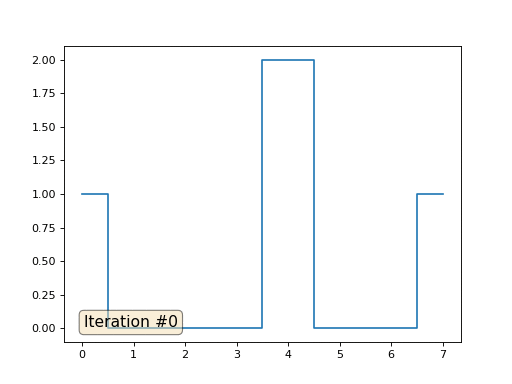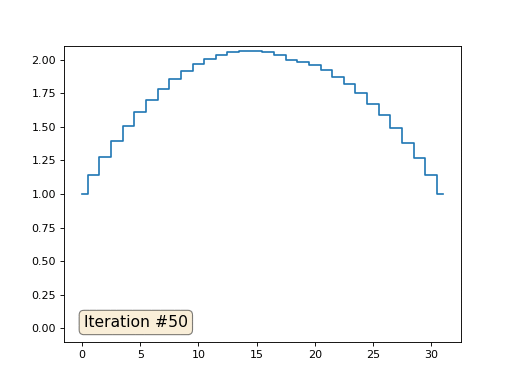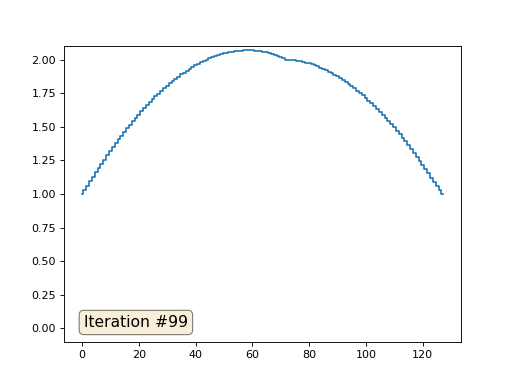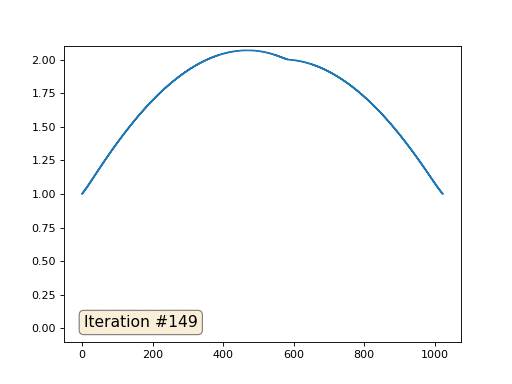
А можно не выпендриваться, и использовать настоящие солверы систем уравнений. Вот я решаю этот же пример, построив матрицу A и столбец b, затем решив матричное уравнение Ax=b:
import numpy as np
import matplotlib.pyplot as plt
n=1000
x = [0.] * n
x[0] = x[-1] = 1.
m = n*57//100
x[m] = 2.
A = np.matrix(np.zeros((n, n)))
for i in range(1,n-2):
A[i, i-1] = -1.
A[i, i] = 2.
A[i, i+1] = -1.
A = A[1:-2,1:-2]
A[m-2,m-1] = 0
A[m-1,m-2] = 0
b = np.matrix(np.zeros((n-3, 1)))
b[0,0] = x[0]
b[m-2,0] = x[m]
b[m-1,0] = x[m]
b[-1,0] = x[-1]
for i in range(n-3):
b[i,0] += 11./n**2
x2 = ((np.linalg.inv(A)*b).transpose().tolist()[0])
x2.insert(0, x[0])
x2.insert(m, x[m])
x2.append(x[-1])
plt.plot(x2, drawstyle='steps-mid')
plt.show()
А вот так выглядит результат работы этой программы, заметим, что решение получилось мгновенно:
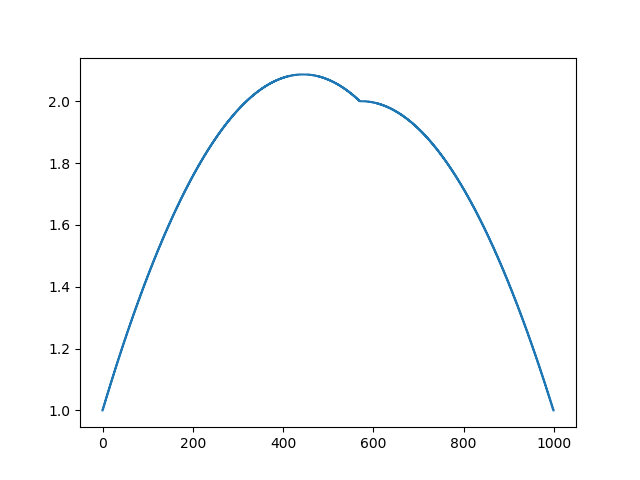
Таким образом, действительно, наша функция кусочно-квадратичная (вторая производная равна константе). В первом примере мы задали нулевую вторую производную, в третьем ненулевую, но везде одинаковую. А что было во втором примере? Мы решили дискретное уравнение Пуассона, задав кривизну поверхности. Напоминаю, что произошло: мы посчитали кривизну входящей поверхности. Если мы решим задачу Пуассона, задав кривизну поверхности на выходе равной кривизне поверхности на входе (const=1), то ничего не изменится. Усиление характеристических черт лица происходит, когда мы просто увеличиваем кривизну (const=2.1). А если const<1, то кривизна результирующей поверхности уменьшается.
Заключение
Очень много задач обработки данных, в частности, геометрии, могут формулироваться как решение системы линейных уравнений. В данной статье я не рассказал, как строить эти системы, моей целью было лишь показать, что это возможно. Темой следующей статьи будет уже не «почему», но «как», и какие солверы потом использовать.
Кстати, а ведь в названии статьи присутствуют наименьшие квадраты. Увидели ли вы их в тексте? Если нет, то это абсолютно не страшно, это именно ответ на вопрос «как?». Oставайтесь на линии, в следующей статье я покажу, где именно они прячутся, и как их модифицировать, чтобы получить доступ к крайне мощному инструменту обработки данных. Например, в десяток строк кода можно получить вот такое:
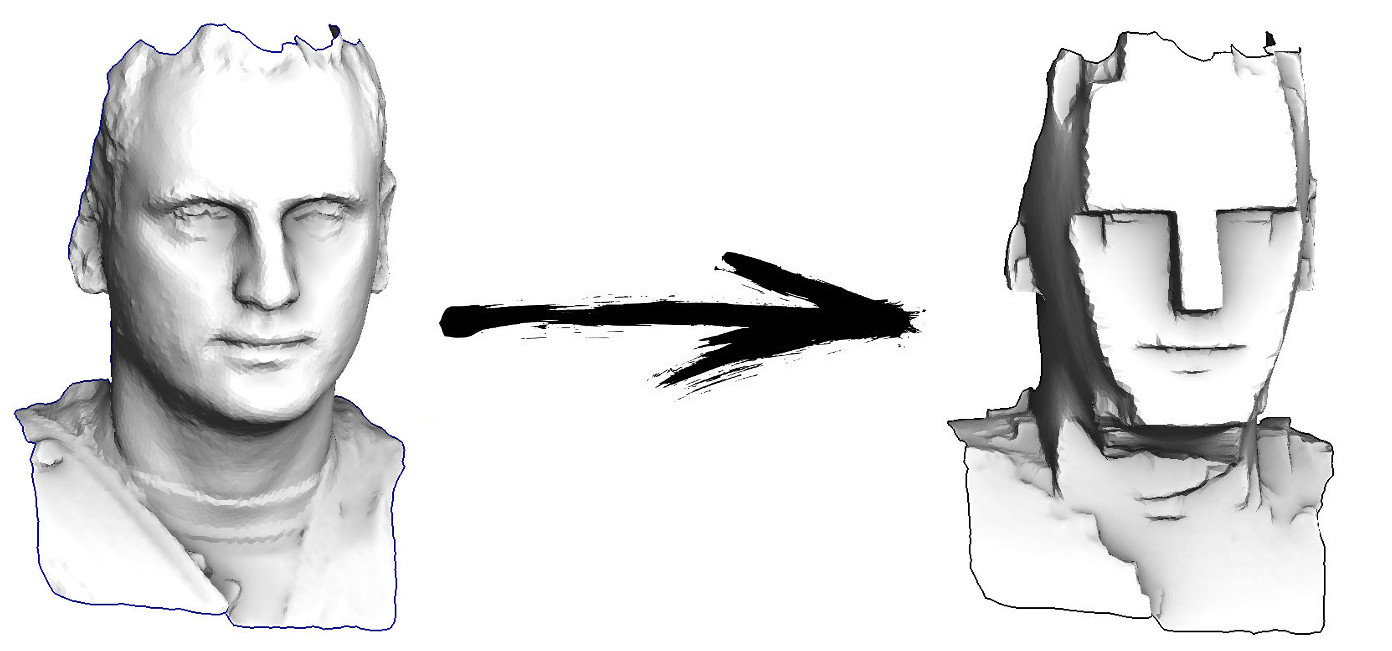
Stay tuned for more!
Автор: haqreu
