Предыдущий мой пост был посвящен цикловым перестановочным оптимизациям, проблемам распознавания циклов, разрешению неоднозначности при работе с памятью, определению и важности зависимостей. Теперь я хочу сделать обзор одной из самых эффективных цикловых оптимизаций — автовекторизации. Хочется обсудить вопросы эффективности оптимизации, а также попытаться понять, какие факторы эту эффективность определяют. Всем, кому это интересно – добро пожаловать. При обсуждении я буду ориентироваться на интеловский автовекторизатор и автовекторизатор gcc 4.7.2. gcc я буду исследовать, чтобы подтвердить, что те принципы векторизации, которые я здесь пытаюсь сформулировать, имеют достаточно общую природу. Заодно мне, конечно, хочется понять уровень автовекторизации в gcc. Тут, конечно, есть некий элемент неравенства, поскольку я использую последний компилятор Интел, но не самую топовую версию gcc, но в основном я буду ориентироваться при сравнении на SSE инструкции. (Кстати, Intel активно участвует в разработке автовекторизатора gcc). Поскольку Intel и интеловский компилятор мне ближе, то ему я уделю кое-где больше внимания. Я не претендую на то, что я векторизаторный гуру и буду рад, если кто-то увидит мои ошибки и меня поправит. Букв будет много.
Откуда есть пошла векторизация
Начиная с самых первых суперкомпьютеров, предпринимались попытки реализовать архитектурные механизмы для использования параллелизма данных (data parallelism) для ускорения вычислений. Во многих вычислительных программах одна и та же операция применяется к целому набору данных, обычно это секция массива или массив. В этом случае существует некоторая повторяющаяся модель доступа к данным, а также операции, которые могут выполняться параллельно над элементами из этого набора данных. Первые конвейерные векторные процессоры поддерживали наборы инструкций, которые выполнялись над векторами данных. Эти данные распологались прямо в памяти. В процессоре Cray-1 были введены векторные регистры, что сильно ускорило выполнение инструкций, поскольку векторные регистры могли сохранять промежуточные результаты вычислений. Использование векторных архитектурных механизмов может программироваться напрямую. Ну а в том случае, если уже имеется программа, написанная с использованием последовательно выполняющихся вычислений, необходимо модифицировать программу для использования параллелизма данных. Эта модификация последовательного алгоритма в параллельный с использованием параллелизма данных и называется векторизацией.
История векторизации и автовекторизации для Intel64 и IA32 архитектур Intel в изложении для чайников выглядит, наверное, так. В славные добрые времена микропроцессора 8086, почтенного отца всего семейства процессоров архитектуры x86, этот процессор работал в тесном сотрудничестве с математическим сопроцессором, который был предназначен для поддержки вычислений для чисел с плавающей точкой, являлся отдельной микросхемой и устанавливался в специальный разъем на материнской плате. Многие старожилы помнят, что при покупке персональных компьютеров нужно было решить дилемму, покупать вычислительную систему с сопроцессором (дороже) или без (дешевле, но медленее при вещественных вычислениях). Сопроцессор поддерживал набор команд x87 и работал с регистровым стеком. Начиная с процессора Intel486DX, сопроцессор был интегрирован в процессор как устройство обработки чисел с плавающей точкой FPU. Эта интеграция добавила в микропроцессор новые регистры, а именно 8 80-битных регистров данных для хранения чисел с плавающей точкой. Но при целочисленных вычислениях эти ресурсы никак не использовались. Решено было на базе FPU обрабатывать целочисленные вектора и предложено расширение MMX, впервые появившееся в процессоре Pentium MMX. В МП добавлялись новые регистры (8 64 битных MM0-MM7), которые адресовались (алиасились) к FPU регистрам, и набор инструкций микропроцессора дополнялся рядом инструкций (SIMD Single Instruction, Multiple Data), работающих с этими регистрами и выполнявшими над ними целочисленные операции. Вводилась концепция пакетов, т.е. каждый из этих регистров мог хранить
2 – 32 битных целых числа
4 — 16 битных
8 — 8 битных
Недостатком была невозможность одновременно работать с целочисленными пакетами и вещественными числами. Необходимо было переключать процессор в специальный режим и это переключение выполнялось достаточно долго.
Следующим этапом была разработка расширения SSE, которое впервые было реализовано в Pentium3. Был увеличен размер векторных регистров до 128 бит. Появление этого набора инструкций позволило решить проблему одновременной работы с упакованными целыми и вещественными данными. Теперь упакованные целые обрабатывались с помощью MMX, в то же время вещественные вычисления проводятся с помощью SSE и векторных регистров. Помимо векторных регистров, SSE добавил в вычислительную систему 32-битный регистр флагов и операции с этим регистром и расширил набор SIMD операций над целыми. Были добавлены инструкции явной предвыборки данных, контроля кэширования данных и контроля порядка операций сохранения, расширения инструкций CPUID для получения информации о процессоре.
За SSE последовало расширение SSE2, которое добавило новые инструкции в SSE с целью полного вытеснения MMX и обработку упакованных данных с плавающей точкой двойной точности.
SSE3, SSEE3, SSE4 — последующие SSE расширения.
AVX новое расширение системы команд, увеличивающее размер векторных регистров до 256 бит.
AVX2 — новое анонсируемое расширение системы команд AVX. Оно уже здесь.
Автовекторизаторы
В современном конкурентном мире часто рулит термин «экономическая эффективность». Поэтому новые команды появляются в процессорах не просто так, а чтобы сделать выпускаемый продукт более привлекательным для покупателей и мотивировать их на замену старых вычислительных архитектур на новые, более производительные, энергоэффективные, крутые и модные. Есть даже специальная независимая площадка, где разработана методология, как правильно мериться крутизной и производительностью. И если модификация и оптимизация существующих инструкций и улучшение архитектуры сразу же могут положительно сказаться на производительности, то с новыми инструкциями нужно работать. Например, уговаривать производителей компиляторов включить их поддержку в свои продукты и отслеживать синхронное появление этих продуктов на рынке вместе с новыми архитектурами. Понятно, что такая ситуация выглядит слегка оптимистичной, поэтому Intel достаточно давно попыталась взять судьбу продвижения своих вычислительных систем в собственные руки и по сути предлагает вместе с вычислительной системой все необходимые компоненты для ее максимально успешного использования, такие как компиляторы и анализаторы производительности. Поэтому новые версии компиляторов выходят одновременно с появлением на рынке знаковых новых архитектур.
Для того, чтобы показать выигрыш от появления новых векторных инструкций, в компиляторе необходим автовекторизатор, т.е. компилятор должен уметь сам осуществлять преобразование скалярного кода в векторный. Сравнение производительности вычислительных систем производится на репрезентативных выборках программ (таких как сюиты CPU2000, CPU2006, CPUV6 и так далее). Возможность завекторизовать что-либо с помощью ассемблерных вставок или вызовов встроенных векторных интринсиков не входит в условие соревнования. При подготовке участника соревнования (компиляции программы перед измерением ее производительности) возможна только передача компилятору набора различных компиляторных опций. Поэтому наличие качественного автовекторизатора — важное условие продвижения на рынке новых вычислительных систем, как интеловских, так и вычислительных систем конкурентов. Неудивительно, что разработка принципов автоматической автовекторизации является одним из локомотивов развития всей информатики (computer science).
Автовекторизатор имеет также большую самостоятельную ценность, как важный компонент оптимизирующего компилятора, позволяющий сравнительно легко улучшать производительность вычислительных программ. Векторизация может выполняться различными способами. Можно использовать ассемблерные вставки, можно использовать вызов встроенных интринсиков. В любом случае такой подход к векторизации имеет ряд недостатков. Он достаточно трудоемок, необходимо портировать код для новых вычислительных систем при появлении новых векторных расширений и т.д. Хотя в этом случае можно добиться лучших результатов, чем при использовании автовекторизатора, но это непростая работа. Гораздо перспективнее, с точки зрения производителя, использовать автовекторизатор.
Достоинство автовекторизатора в том, что достаточно добавить опции при компиляции, и компилятор сам выполнит векторизацию тех циклов, которые выгодно векторизовать. Автовекторизатор Интел сейчас работает по умолчанию, поскольку дефолтный уровень оптимизации –O2. Автовекторизатор gcc работает, начиная с опции –O3. И тот и другой автовекторизаторы можно включить/отключить cпециальными опциями. Автовекторизатор позволяет создавать приложения, ориентированные на выполнение на конкретной вычислительной системе, поддерживающей определенное векторное расширение. В Intel компиляторе существует несколько разных возможностей для выбора архитектуры. Обычный режим, когда выбирается используемое векторное расширение, ничем не отличается от того, как векторное расширение выбирается в gcc. Но для интеловских архитектур можно включать проверки времени выполнения и создавать, например, многовариантные приложения, с различными вариантами векторизации, выбирая оптимальный вариант в зависимости от архитектуры, на которой выполняется программа. Можно автоматически выполнять оптимальную векторизацию для машины, на которой выполняется компиляция. Т.е. для компилятора icc существуют интеловские архитектуры и все остальные. Боюсь, что тонкий тюнинг векторизации для второго вида архитектур не предусматривается. Могу предположить, что автовекторизатор gcc — больший сторонник равноправия.
Для более качественного использования автовекторизатора желательно иметь с ним обратную связь. Если автовекторизатор сообщает о результатах своей работы, т.е. сообщает, какое решение он принял при векторизации в том или ином случае, то можно пытаться разбираться с проблемами, мешающими векторизации. И icc и gcc имеют такую функциональность. icc имеет опцию –vec_report, а gcc выдает отчет о работе автовекторизатора с помощью опции –ftree-vectorizer-verbose. Понятно, что рапорт icc заточен на пользователей, в то время как рапорт gcc – на разработчиков. Повышая уровень отчетности у gcc, можно получить массу интересных деталей о «мыслительном процессе» автовектризатора, что достаточно интересно, поскольку коммерческий icc неохотно делится своими секретами. С другой стороны, если важные детали у gcc нужно отлавливать в куче другой информации, то icc достаточно лаконичен.
Пример использования автовекторизатора
Давайте возьмем простую функцию и попробуем посмотреть на диагностику векторизаторов.
void Calculate(float * a,float * b, float * c , int n) {
for(int i=0;i<n;i++) {
a[i] = a[i]+b[i]+c[i];
}
return;
}
gcc -c -O3 -march=native -std=c99 -mfpmath=sse -ftree-vectorizer-verbose=2 vector.c
Analyzing loop at vector.c:2
Vectorizing loop at vector.c:2
2: created 2 versioning for alias checks.
2: LOOP VECTORIZED.
vector.c:1: note: vectorized 1 loops in function.
Не забываем при работе с вещественными добавить для gcc –mfpmath=sse, иначе векторизатор не работает.
Ну и аналогично для icc:
icc -c -vec_report3 -xhost -std=c99 vector.c
vector.c(2): (col. 3) remark: LOOP WAS VECTORIZED
vector.c(2): (col. 3) remark: loop skipped: multiversioned
Примерная схема векторизации простейшего цикла
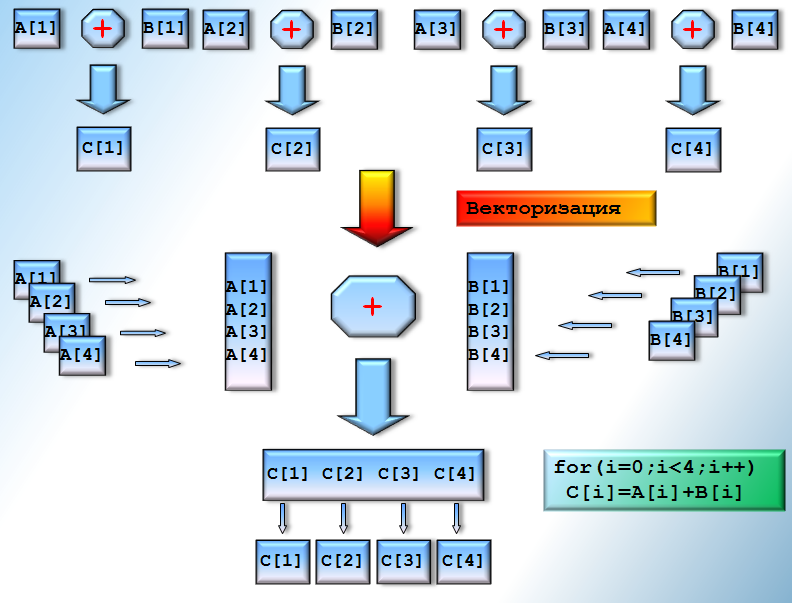
В основном векторизация выполняется для циклов, и в этом случае это цикловая перестановочная оптимизация. Именно такую векторизацию я и хотел бы рассмотреть. Здесь я попытался нарисовать некую схему векторизации. До векторизации мы имеем какие-то наборы однотипных данных и над элементами этих наборов мы производим однотипные операции и сохраняем результат вычислений. При векторизации этого последовательного кода необходимо сформировать из скалярных данных вектора (записать данные в векторные регистры), применить к этим векторам векторную операцию и затем результат из векторного регистра сохранить в память. Если векторизуется простой цикл с одним утверждением внутри, то можно представить в качестве первого этапа векторизации развертку (unrolling) этого цикла на число N, которое равно количеству элементов используемого типа в векторном регистре. В результате векторизации цикла одна векторная итерация заменяет N скалярных итераций. В общем случае можно считать, что при векторизации данные нужно «упаковывать» в векторные регистры. Хотя операндами векторных инструкций могут быть адреса памяти, но эти адреса должны быть выравнены по памяти и в большинстве случаев векторизатору нужно работать, чтобы обеспечить выполнение этого условия.
Допустимость векторизации
Поскольку мы рассматриваем векторизацию как цикловую оптимизацию, то она выполняется только для «хороших» циклов, т.е. циклов, имеющих определенное количество итераций и последовательно изменяющиеся итерационные переменные. То есть для того, чтобы автовекторизатор смог векторизовать циклы, они сначала должны быть распознаны. Какие трудности приходится преодолеть компилятору при распознавании циклов, я описал в предыдущем посте.
Векторизация цикла меняет порядок выполнения операций в цикле. Если тело цикла содержит несколько утверждений для вычисления (statements), то изменяется порядок выполнения этих утверждений так, как показано на схеме:
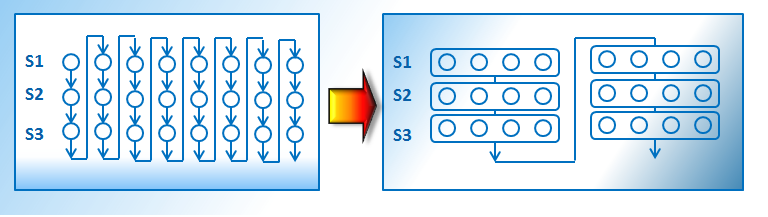
Согласно критерию допустимости перестановочных оптимизаций векторизация допустима, если не меняется порядок зависимых вычислений. В силу особенностей векторизации она не меняет порядок лексических зависимостей по данным вперед (lexically forward data dependencies), но может нарушать привнесенные циклом самозависимости и обратные зависимости (self and backward dependencies). Будут ли нарушены такие зависимости — зависит от дистанции между зависимыми утверждениями. Если эта дистанция больше N (количество элементов данного типа в векторном регистре), то зависимости не будут нарушены. Интересно также, что так называемые «зависимости вывода» могут не нарушаться при векторизации, если сохранение в векторные регистры и выгрузка из них осуществляются последовательно, т.е. в том же порядке, что и в программе.
Для того, чтобы понять, допустима ли векторизация, необходимо произвести анализ зависимостей. Самый плохой случай — в цикле существуют разные объекты, которые могут ссылаться на одну и ту же память. И если вернуться к нашему первому примеру, то именно такую ситуацию мы здесь и имеем. Если функция Calculate компилируется отдельно, то в общем случае указатели a,b,c могут ссылаться на одну и ту же или пересекающуюся память. Как видно из отчетов, оба векторизатора справились с этой работой путем добавления проверок времени выполнения и многоверсионного кода (хотя говорят об этом разным языком). В результате в код добавились дополнительные инструкции. Теперь в случае, если некие сегменты памяти, начинающиеся с указателей a,b,c и имеющие размер n*sizeof(float) не пересекаются, то вызывается векторизованный цикл, а в противоположном случае – скалярный. Код функции существенно увеличился, проверки времени выполнения снижают производительность.
Сделать автовекторизацию более оптимальной можно несколькими способами, а именно: либо самому передать компилятору информацию о том, что объекты не пересекаются по памяти, либо добавить межпроцедурный анализ, в надежде, что компилятор сам сможет это доказать. Межпроцедурный анализ – это другая большая отдельная тема. Но понятно, что теоретически мы можем проверить, алиасятся ли по памяти актуальные аргументы при всех вызовах функции Calculate, и если нет, то распространить это знание на формальные аргументы функции Calculate. Расширим немного самый первый тест и посмотрим, умееют ли компиляторы протягивать такую информацию.
#include <stdlib.h>
#define N 2000
static void Calculate(float * a,float * b, float * c , int n) {
for(int i=0;i<n;i++) {
a[i] = a[i]+b[i]+c[i];
}
return;
}
float test() {
float *x,*y,*z,ret;
x=(float*)malloc(N*sizeof(float));
y=(float*)malloc(N*sizeof(float));
z=(float*)malloc(N*sizeof(float));
for(int i=0;i<N;i++) {
x[i] = 1.0;y[i] = 0.0; z[i] = 1.0;
}
Calculate(x,y,z,N);
ret=x[1];
free(x); free(y);free(z);
return ret;
}
При компиляции запретим инлайнинг, чтобы сохранить функцию Calculate. Здесь межпроцедурный анализ используется только для функций из исходного файла vector.c и аттрибут static позволяет компилятору понять, что нет вызовов этой функции где-то в других исходных файлах и функция может быть модифицирована в соответствии с обнаруженными свойствами ее актуальных аргументов.
gcc -c -O3 -fno-inline -fipa-pta -march=native -std=c99 -mfpmath=sse -ftree-vectorizer-verbose=2 vector.c
...
Vectorizing loop at vector.c:5
5: LOOP VECTORIZED.
...
icc -c -ip -ip-no-inlining -vec_report3 -xhost -std=c99 vector.c
vector.c(5): (col. 3) remark: LOOP WAS VECTORIZED
vector.c(5): (col. 3) remark: REMAINDER LOOP WAS VECTORIZED
Для gcc необходимо добавить опцию -fipa-pta (Perform interprocedural pointer analysis and interprocedural modification and reference analysis), поскольку эта опция не входит в дефолтные опции оптимизации. В данном случае gcc и icc успешно справились с задачей протяжки свойств актуальных аргументов.
Чтобы не напрягать лишний раз компилятор анализом программы, проще к описаниям указателей добавить квалификатор restrict, чтобы указать компилятору на то, что данные, на которые ссылается указатель, могут быть адресованы только с его помощью. Если в цикле нет объектов, которые могут алиаситься, то анализ зависимостей должен уметь находить зависимости (например, обращение к одному и тому же элементу массива на разных итерациях цикла), определять их тип, дистанцию между зависимыми итерациями, хронологический их порядок и определять допустимость трансформации. Работа совсем непростая.
Посмотрим, как работают автовекторизаторы, информируя пользователя о проблемах. Рассмотрим несколько типичных случаев, когда зависимости могут влиять на векторизацию:
void Calculate(float * restrict a,float *restrict b,float * restrict c, int * restrict vec, int n) {
for(int i=0;i<n-3;i++) //3
a[i+3] = a[i]+1;
for(int i=0;i<n-5;i++) //5
a[i+5] = a[i]+1;
for(int i=3;i<n;i++) //7
a[i-3]=a[i]+1;
for(int i=0;i<n;i++) //9
b[i]=a[vec[i]];
for(int i=0;i<n;i++) //11
a[vec[i]] = b[i]*vec[i];
for(int i=1;i<n;i++) { //13
a[i]=c[i]+1;
b[i]=a[i-1];
}
for(int i=0;i<n-1;i++) { //17
a[i]=c[i]+1;
b[i]=a[i+1];
}
for(int i=0;i<n-5;i++) { //21
a[i]=c[i]+1;
b[i]=a[i+5];
}
return;
}
В первых двух циклах имеем лексически обратные зависимости (backward dependencies) и дистанция между зависимостями 3 и 5. При работе с 128 битовыми регистрами (SSE) это мешает сделать векторизацию на всю ширину векторного регистра для первого цикла. При работе с 256 битовыми регистрами (AVX) векторизация на всю ширину векторного регистра невозможна и во втором случае. В третьем цикле имеется зависимость вперед (forward dependence), которая не препятствует векторизации. Четвертый и пятый циклы – это случаи векторной индексации. В пятом случае существует выходная зависимость (output dependence), т.е. имеет значение порядок записи в память. Такая зависимость не мешает векторизации, поскольку, хотя выполняются векторные операции, но в память результаты из векторных регистров извлекаются последовательно и это, в итоге, помогает сохранить правильный результат. В шестом цикле есть зависимость вперед между двумя утверждениями цикла. Седьмой и восьмой случай – обратные зависимости.
gcc -c -O3 -fno-inline -march=corei7-avx -std=c99 -mfpmath=sse -ftree-loop-distribution -ftree-vectorizer-verbose=1 vector.c
Analyzing loop at vector.c:21
Vectorizing loop at vector.c:21
21: LOOP VECTORIZED.
Analyzing loop at vector.c:17
Analyzing loop at vector.c:13
Vectorizing loop at vector.c:13
13: LOOP VECTORIZED.
Analyzing loop at vector.c:11
Analyzing loop at vector.c:9
Analyzing loop at vector.c:7
Vectorizing loop at vector.c:7
7: LOOP VECTORIZED.
Analyzing loop at vector.c:5
Vectorizing loop at vector.c:5
5: LOOP VECTORIZED.
Analyzing loop at vector.c:3
vector.c:1: note: vectorized 4 loops in function.
Gcc не захотел рассматривать циклы с векторной индексацией. В циклах с обратными зависимостями посчитал дистанции и завекторизовал их, где это возможно. При этом он понизил базу векторизации для циклов //5 и //21, т.е. сделал векторизацию для 128 битовых регистров. Об этом можно узнать, увеличив значение для –ftree-vectorizer-verbose.
…
21: === vect_analyze_dependences ===
21: dependence distance = 5.
21: adjusting maximal vectorization factor to 5
21: dependence distance >= VF.
21: bad data dependence.
21: ***** Re-trying analysis with vector size 16
Аналогично для icc получаем.
icc -c -ip -vec_report3 -xAVX -std=c99 vector.c
vector.c(3): (col. 3) remark: loop was not vectorized: existence of vector dependence
vector.c(4): (col. 7) remark: vector dependence: assumed FLOW dependence between a line 4 and a line 4
vector.c(5): (col. 3) remark: LOOP WAS VECTORIZED
vector.c(7): (col. 3) remark: LOOP WAS VECTORIZED
vector.c(9): (col. 3) remark: LOOP WAS VECTORIZED
vector.c(9): (col. 3) remark: REMAINDER LOOP WAS VECTORIZED
vector.c(11): (col. 3) remark: LOOP WAS VECTORIZED
vector.c(13): (col. 3) remark: LOOP WAS VECTORIZED
vector.c(17): (col. 3) remark: PARTIAL LOOP WAS VECTORIZED
vector.c(17): (col. 3) remark: PARTIAL LOOP WAS VECTORIZED
vector.c(21): (col. 3) remark: PARTIAL LOOP WAS VECTORIZED
vector.c(21): (col. 3) remark: PARTIAL LOOP WAS VECTORIZED
icc не векторизовал только цикл //3. Интересно, что цикл //17 был предварительно разбит (distribution) на два, и затем оба векторизованы. То же самое было проделано для цикла //21, хотя в этом необходимости не было.
ftree-loop-distribution мог помочь gcc векторизовать цикл //17, предварительно разбив его на два, но почему-то этого не сделал.
Еще один интересный пример выглядит так. Собственно, это простейшая работа с квадратными матрицами
void ttt(int *restrict a, int * restrict b, int n) {
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
a[j+n*i] = a[j+n*i] + b[i+n*j];
return;
}
icc векторизует внутренний цикл успешно, а gcc пишет «not suitable for gather» (?).
gcc -c -fno-inline -O3 -march=corei7 -std=c99 -mfpmath=sse -ftree-vectorizer-verbose=3 vector.c
Analyzing loop at vector.c:8
8: not vectorized: data ref analysis failed D.2238_18 = *D.2237_17;
Analyzing loop at vector.c:9
9: not vectorized: not suitable for gather D.2238_18 = *D.2237_17;
vector.c:6: note: vectorized 0 loops in function.
Когда я рассказывал о критерии допустимости перестановочных оптимизаций, то уже упоминал, что существуют директивы, которые можно использовать, чтобы передать автовекторизатору сокровенное знание о программе. Например, вы используете векторную индексацию и знаете, что каждый векторный индекс уникален. Тогда зависимостей, вызванных использованием такой индексации, быть не может. Например:
void Calculate(float * restrict a,float *restrict b,float * restrict c, int * restrict vec, int n) {
for(int i=0;i<n;i++)
a[vec[i]] += b[i]*c[i];
return;
}
Т.е. здесь может быть зависимость, если есть одинаковые vec[i] и vec[j]. Как я уже выяснил, gcc не понимает векторной индексации. icc выдает следующую диагностику:
icc -c -vec_report3 -xSSE4.2 -std=c99 vector.c
ector.c(3): (col. 3) remark: loop was not vectorized: existence of vector dependence
vector.c(4): (col. 7) remark: vector dependence: assumed ANTI dependence between a line 4 and a line 4
vector.c(4): (col. 7) remark: vector dependence: assumed FLOW dependence between a line 4 and a line 4
vector.c(4): (col. 7) remark: vector dependence: assumed FLOW dependence between a line 4 and a line 4
vector.c(4): (col. 7) remark: vector dependence: assumed ANTI dependence between a line 4 and a line 4
Эту проблему можно решить, поместив перед циклом #pragma ivdep. Эта прагма утверждает, что в цикле не существует ни одной предполагаемой зависимости. После подстановки этой прагмы компилятор успешно векторизует этот цикл.
В случаях более сложных циклов рапорт векторизатора может дать представление о зависимостях, препятствующих векторизации. Изучив эти проблемы, можно оценить вызваны ли они реально существующими зависимостями или просто компилятор не в состоянии доказать отсутствие зависимостей. Во втором случае можно улучшить работу автовекторизатора с помощью #pragma ivdep.
С удивлением обнаружил, что gcc компилятор эту прагму не поддерживает и соответствующий трэкер существует с 2007 года.
Факторы, определяющие эффективность векторизации: Последовательный доступ
Из схемы видно, что в результате векторизации сокращается количество выполняемых арифметических операций, но при этом возникает необходимость «упаковывать» данные в векторные регистры. Данные могут быть помещены в векторные регистры поэлементно или с помощью одного копирования из памяти. Если элементы не расположены в памяти непрерывно, то загрузка в регистры может производится только поэлементно. Если в векторизуемом утверждении чтение/запись являются основными операциями, то выгода от векторизации становится сомнительной – при векторизации количество выполняемых операций изменяется незначительно. Но при этом в векторном случае значительно увеличивается количество кода (как при развертке на N), а это тоже может плохо влиять на производительность.
Если, для примера, рассмотреть простейший цикл, в котором доступ к массивам осуществляется с шагом 2
void Calculate(int * restrict a, int * restrict b, int n) {
for(int i=0;i<n;i=i+2) {
b[i] = a[i]+1;
}
return;
}
то при векторизации можно получить примерно такой ассемблер для векторизованной части цикла (использую интеловский автовекторизатор для своих примеров):
icc -S -xSSE4.2 -std=c99 vector.c
..B1.8: # Preds ..B1.8 ..B1.7
movd 24(%edi,%eax,8), %xmm1 #4.14
movd 8(%edi,%eax,8), %xmm3 #4.14
movd 16(%edi,%eax,8), %xmm2 #4.14
movd (%edi,%eax,8), %xmm4 #4.14
punpckldq %xmm1, %xmm3 #4.14
punpckldq %xmm2, %xmm4 #4.14
punpckldq %xmm3, %xmm4 #4.14
paddd %xmm0, %xmm4 #4.7
movd %xmm4, (%esi,%eax,8) #4.7
psrldq $4, %xmm4 #4.7
movd %xmm4, 8(%esi,%eax,8) #4.7
psrldq $4, %xmm4 #4.7
movd %xmm4, 16(%esi,%eax,8) #4.7
psrldq $4, %xmm4 #4.7
movd %xmm4, 24(%esi,%eax,8) #4.7
addl $4, %eax #3.4
cmpl %edx, %eax #3.4
jb ..B1.8 # Prob 82%
Этот пример говорит сам за себя. Несколько векторных регистров используются для формирования вектора a[i:i+N]. Тело цикла значительно разрастается и, наверное, трудно ожидать улучшения производительности от такой векторизации.
Продвинутые векторизаторщики могут спросить, а как-же scatter/gathering? На данный момент реализация gather выполнена для вычислительных машин, поддерживающих AVX2. По крайней мере, gather уменьшает количество инструкций. В данном случае:
icc -S -xCORE-AVX2 -std=c99 vector.c
.B1.8: # Preds ..B1.8 ..B1.7
lea (%edi,%eax,8), %ebx #4.14
vpxor %ymm3, %ymm3, %ymm3 #4.14
vpcmpeqd %ymm2, %ymm2, %ymm2 #4.14
vpgatherdd %ymm2, (%ebx,%ymm0,8), %ymm3 #4.14
vpaddd %ymm1, %ymm3, %ymm4 #4.19
vextracti128 $1, %ymm4, %xmm2 #4.7
vpsrldq $4, %xmm4, %xmm5 #4.7
vmovd %xmm4, (%esi,%eax,8) #4.7
vpsrldq $4, %xmm2, %xmm3 #4.7
vpsrldq $4, %xmm5, %xmm6 #4.7
vpsrldq $4, %xmm3, %xmm4 #4.7
vmovd %xmm5, 8(%esi,%eax,8) #4.7
vpsrldq $4, %xmm6, %xmm7 #4.7
vpsrldq $4, %xmm4, %xmm5 #4.7
vmovd %xmm6, 16(%esi,%eax,8) #4.7
vmovd %xmm7, 24(%esi,%eax,8) #4.7
vmovd %xmm2, 32(%esi,%eax,8) #4.7
vmovd %xmm3, 40(%esi,%eax,8) #4.7
vmovd %xmm4, 48(%esi,%eax,8) #4.7
vmovd %xmm5, 56(%esi,%eax,8) #4.7
addl $8, %eax #3.4
cmpl %edx, %eax #3.4
jb ..B1.8
Последовательный доступ позволяет упростить процедуру загрузки памяти в регистры, поэтому векторизация будет тем более эффективной, чем к большему количеству объектов в цикле используется последовательный доступ. С другой стороны, если векторизуемый код содержит много вычислений и их переиспользование, то векторизация может быть достаточно эффективной и при непоследовательном доступе к объектам.
Факторы, определяющие эффективность векторизации: Выравнивание
Скорость копирования из памяти также зависит от того, каким образом записываемый в векторный регистр блок памяти выровнен. В случае, если происходит работа с выровненными адресами, то эти адреса можно использовать в инструкциях как операнды, и за счет этого может быть осуществлено более оптимальное распределение регистров. Чтение по выровненным адресам осуществляется быстрее. Для SSE инструкций требуются адреса, выровненные на 16, для AVX – на 32.
Из-за влияния выравнивания на производительность общая схема векторизации цикла выглядит примерно так:
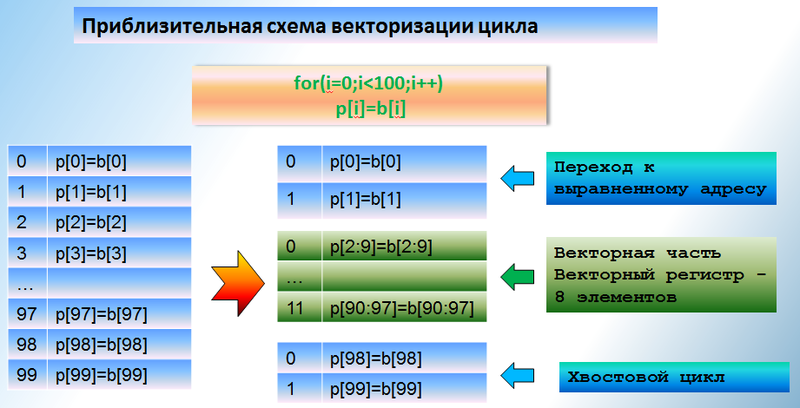
Векторизация цикла в общем случае порождает три цикла: цикл для достижения выровненых по памяти элементов какого-либо обрабатываемого объекта, векторизованная часть и хвостовой скалярный цикл. Если внутри цикла обрабатываются несколько объектов, то все их выровнять не получается и необходимо выбрать «ведущий» объект и подстраиваться под него.
Чтобы оценить влияние выравнивания давайте придумаем простенький тест, который будет работать как с выровненной, так и с невыровненной памятью. С помощью макроса PERF мы создаем два варианта программы. В одном в функцию ttt будут передаваться аргументы выровненные по-разному, в другом — одинаково. Изучение ассемблерных файлов приводит к мысли, что и icc, и gcc в качестве «ведущего» массива выбрали массив «a». Поэтому перед векторным циклом будут вставлены несколько скалярных итераций для его выравнивания. А массив «b» будет выравнен в одном варианте программы, а в другом – нет. Ну и запретим подстановку, чтобы тело функции было одинаково для обоих выполняемых файлов. Выровненную память для обрабатываемых массивов выделим с помощью memalign.
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#define N 1000
void ttt(int * restrict a, int * restrict b, int n) {
for(int i=0;i<n;i++) {
a[i] = a[i]+b[i];
}
return;
}
int main() {
int *a,*b;
a = (int*)memalign(32,N*sizeof(int));
b = (int*)memalign(32,N*sizeof(int));
for(int i=0;i<N;i++) {
a[i]=i; b[i]=i;
}
for(int rep=0; rep<10000000; rep++) {
#ifndef PERF
ttt(&a[0],&b[1],N-3);
ttt(&a[1],&b[2],N-4);
#else
ttt(&a[0],&b[0],N-3);
ttt(&a[1],&b[1],N-4);
#endif
}
printf("%dn",a[100]);
free(a); free(b);
}
icc -ip-no-inlining -vec_report3 -xSSE4.2 -std=c99 vector.c -o vector_sse
icc -DPERF -ip-no-inlining -vec_report3 -xSSE4.2 -std=c99 vector.c -o vector_sse_perf
На моей лабораторной машинке получаю такие циферки:
time ./vector_sse : 6.36s
time ./vector_sse_perf : 3.46s
Не ожидал такой разницы. Понятно, что здесь все данные распологаются в кэше. В реальной программе такую разницу из-за выравнивания, наверное, труднее получить.
Смотрим, а что покажет gcc в этой ситуации:
gcc -fno-inline -O3 -march=corei7 -std=c99 -mfpmath=sse -ftree-vectorizer-verbose=1 vector.c -o vector
gcc -fno-inline -DPERF -O3 -march=corei7 -std=c99 -mfpmath=sse -ftree-vectorizer-verbose=1 vector.c -o vector_perf
time ./vector : 6.49s
time ./vector_perf : 3.61s
Т.е. можно сделать вывод, что выравнивание очень благотворно сказываются на производительности в том случае, если в цикле достаточно много итераций.
Поскольку выравнивание так сильно влияет на производительность, то хотелось бы иметь инструменты, позволяющие манипулировать этой характеристикой. Такие инструменты есть. Если память для массива выделяется на стеке, то можно использовать конструкцию __attribute__((aligned(N)). Например, так:
int a[N] __attribute__((aligned(32)));
С помощью этого атрибута можно выравнивать и массивы расположенные внутри класса или структуры. Я уже использую в своей программе аналог функции malloc, а именно memalign – функцию, которая возвращает выровненную память. Если вы позаботились о выравнивании и хотите, чтобы автовекторизатор создавал код для выровненных по памяти объектов, но при этом программный анализ не позволяет корректно использовать это свойство объекта, то можно использовать встроенную функцию __builtin_assume_aligned, например так:
int * aa =__builtin_assume_aligned(a,32);
В рассматриваемом случае это приведет к тому, что автовекторизатор создаст код без выравнивающего цикла, возможно будет использовать инструкции для работы с выровненной памятью и возможно будет использовать адреса памяти, как операнды для векторных инструкций. (Если первый пункт может просто сказаться на производительности, то последующие приведут к катастрофическим последствиям для работы программы в случае, если реальный объект окажется невыровненным.)
Существует также #pragma vector aligned. Как я понимаю, в случае ее использования все объекты участвующие в векторизации, будут считаться выровненными.
Оценка полезности автовекторизации
Поскольку существуют факторы эффективности векторизации, связанные с работой самой вычислительной системы, то было бы логично как-то учитывать эти факторы при выполнении автовекторизации, чтобы не векторизовать заведомо провальные случаи и не ухудшать производительность приложения. Логично иметь эвристический механизм, который взвесит все факторы за и против векторизации и выдаст свое заключение. Для компилятора icc заключение выглядит примерно так:
vector.c(3): (col. 4) remark: loop was not vectorized: vectorization possible but seems inefficient
Gcc с опцией -ftree-vectorizer-verbose=3 рассказывает о ходе своих рассуждений (например отказывается векторизовать короткий цикл):
8: cost model: prologue peel iters set to vf/2.
8: cost model: epilogue peel iters set to vf/2 because peeling for alignment is unknown .
8: Cost model analysis:
Vector inside of loop cost: 5
Vector outside of loop cost: 24
Scalar iteration cost: 4
Scalar outside cost: 0
prologue iterations: 2
epilogue iterations: 2
Calculated minimum iters for profitability: 7
8: Profitability threshold = 6
8: not vectorized: vectorization not profitable.
Но в целом, поскольку у gcc обнаружились проблемы с векторизацией объектов, доступ к которым осуществляется непоследовательно, мне не удалось найти более сложные примеры, когда gcc отказывается векторизовать цикл из-за неэффективности векторизации.
Если имеются оценочные механизмы для принятия решения о векторизации и пользователь считает, что эвристический механизм сделал неверное заключение о выгодности векторизации, то решение автовекторизатора можно изменить, например, с помощью различных прагм. Например, #pragma vector always рекомендует всегда векторизовать расположенный ниже цикл. В свою очередь, #pragma novector позволяет отказаться от векторизации цикла.
Заключение
Качество работы автовекторизатора отнюдь не исчерпывается всеми теми соображениями, которые были здесь обсуждены. Автовекторизатору для получения оптимального кода необходимо сотрудничать с другими цикловыми оптимизациями, использовать результаты межпроцедурного анализа, уметь распознавать различные идиомы, уметь переиспользовать уже сделанные векторные расчеты и многое другое. Но я надеюсь, что мое краткое введение в тему автовекторизации было полезно.
В целом мне не удалось на самых простых примерах заметить какие-то ошибки автовекторизатора icc. Автовекторизатор же gcc продемонстрировал ряд недостатков (отказался векторизовать массивы с векторной индексацией и случай с непоследовательным доступом для квадратной матрицы).
Некоторая полезная литература по теме
У меня есть замечательная книга «Optimizing compilers for modern architectures». Авторы Randy Allen и Ken Kennedy. Эта книга вводит во все основные аспекты работы оптимизирующего компилятора.
Есть также «The software Vectorization Handbook». Книга инженеров для инженеров, написанная Aart J.C. Bik и посвященная непосредственно теории автовекторизации.
Много интересных статей можно найти на интеловских сайтах. Читайте, например, A Guide to Auto-vectorization with Intel® C++ Compilers.
Автор: andrei_an
