Все чаще замечаю, что современным самоучкам очень не хватает матчасти. Все знают языки, но мало основы, такие как типы данных или алгоритмы. Немного про типы данных.
Еще в далеком 1976 швейцарский ученый Никлаус Вирт написал книгу Алгоритмы + структуры данных = программы.
40+ лет спустя это уравнение все еще верно. И если вы самоучка и надолго в программировании пробегитесь по статье, можно по диагонали. Можно код кофе.

В статье так же будут вопросы, которое вы можете услышать на интервью.
Что такое структура данных?
Структура данных — это контейнер, который хранит данные в определенном макете. Этот «макет» позволяет структуре данных быть эффективной в некоторых операциях и неэффективной в других.
Какие бывают?
Линейные, элементы образуют последовательность или линейный список, обход узлов линеен. Примеры: Массивы. Связанный список, стеки и очереди.
Нелинейные, если обход узлов нелинейный, а данные не последовательны. Пример: граф и деревья.
Основные структуры данных.
- Массивы
- Стеки
- Очереди
- Связанные списки
- Графы
- Деревья
- Префиксные деревья
- Хэш таблицы
Массивы
Массив — это самая простая и широко используемая структура данных. Другие структуры данных, такие как стеки и очереди, являются производными от массивов.
Изображение простого массива размера 4, содержащего элементы (1, 2, 3 и 4).
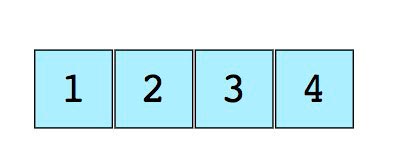
Каждому элементу данных присваивается положительное числовое значение (индекс), который соответствует позиции элемента в массиве. Большинство языков определяют начальный индекс массива как 0.
Бывают
Одномерные, как показано выше.
Многомерные, массивы внутри массивов.
Основные операции
- Insert-вставляет элемент по заданному индексу
- Get-возвращает элемент по заданному индексу
- Delete-удаление элемента по заданному индексу
- Size-получить общее количество элементов в массиве
Вопросы
- Найти второй минимальный элемент массива
- Первые неповторяющиеся целые числа в массиве
- Объединить два отсортированных массива
- Изменение порядка положительных и отрицательных значений в массиве
Стеки
Стек — абстрактный тип данных, представляющий собой список элементов, организованных по принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»).
Это не массивы. Это очередь. Придумал Алан Тюринг.
Примером стека может быть куча книг, расположенных в вертикальном порядке. Для того, чтобы получить книгу, которая где-то посередине, вам нужно будет удалить все книги, размещенные на ней. Так работает метод LIFO (Last In First Out). Функция «Отменить» в приложениях работает по LIFO.
Изображение стека, в три элемента (1, 2 и 3), где 3 находится наверху и будет удален первым.
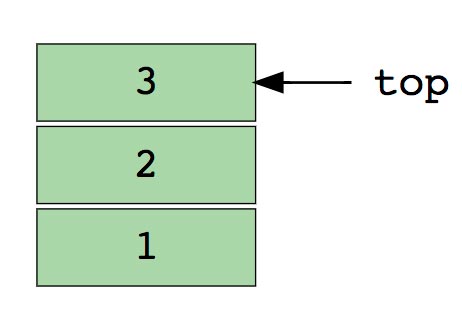
Основные операции
- Push-вставляет элемент сверху
- Pop-возвращает верхний элемент после удаления из стека
- isEmpty-возвращает true, если стек пуст
- Top-возвращает верхний элемент без удаления из стека
Вопросы
- Реализовать очередь с помощью стека
- Сортировка значений в стеке
- Реализация двух стеков в массиве
- Реверс строки с помощью стека
Очереди
Подобно стекам, очередь — хранит элемент последовательным образом. Существенное отличие от стека – использование FIFO (First in First Out) вместо LIFO.
Пример очереди – очередь людей. Последний занял последним и будешь, а первый первым ее и покинет.
Изображение очереди, в четыре элемента (1, 2, 3 и 4), где 1 находится наверху и будет удален первым
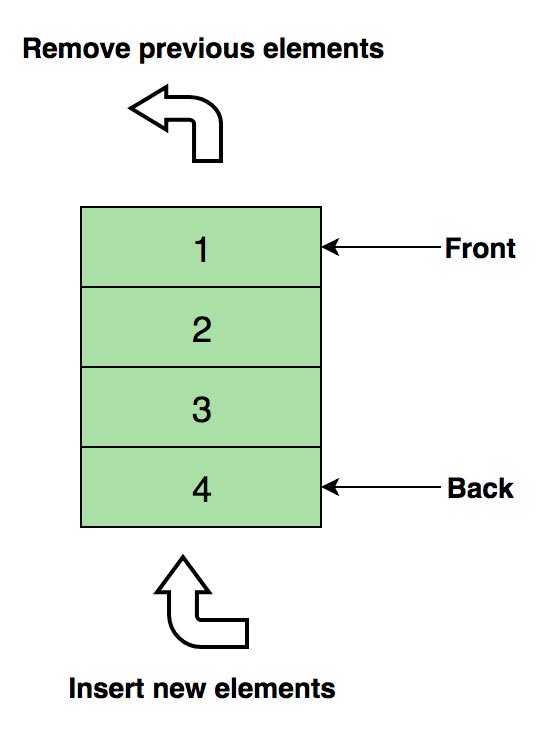
Основные операции
- Enqueue—) — вставляет элемент в конец очереди
- Dequeue () — удаляет элемент из начала очереди
- isEmpty () — возвращает значение true, если очередь пуста
- Top () — возвращает первый элемент очереди
Вопросы
- Реализовать cтек с помощью очереди
- Реверс первых N элементов очереди
- Генерация двоичных чисел от 1 до N с помощью очереди
Связанный список
Связанный список – массив где каждый элемент является отдельным объектом и состоит из двух элементов – данных и ссылки на следующий узел.
Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями.
Бывают
Однонаправленный, каждый узел хранит адрес или ссылку на следующий узел в списке и последний узел имеет следующий адрес или ссылку как NULL.
1->2->3->4->NULL
Двунаправленный, две ссылки, связанные с каждым узлом, одним из опорных пунктов на следующий узел и один к предыдущему узлу.
NULL<-1<->2<->3->NULL
Круговой, все узлы соединяются, образуя круг. В конце нет NULL. Циклический связанный список может быть одно-или двукратным циклическим связанным списком.
1->2->3->1
Самое частое, линейный однонаправленный список. Пример – файловая система.

Основные операции
- InsertAtEnd — Вставка заданного элемента в конец списка
- InsertAtHead — Вставка элемента в начало списка
- Delete — удаляет заданный элемент из списка
- DeleteAtHead — удаляет первый элемент списка
- Search — возвращает заданный элемент из списка
- isEmpty — возвращает True, если связанный список пуст
Вопросы
- Реверс связанного списка
- Определение цикла в связанном списке
- Возврат N элемента из конца в связанном списке
- Удаление дубликатов из связанного списка
Графы
Граф-это набор узлов (вершин), которые соединены друг с другом в виде сети ребрами (дугами).
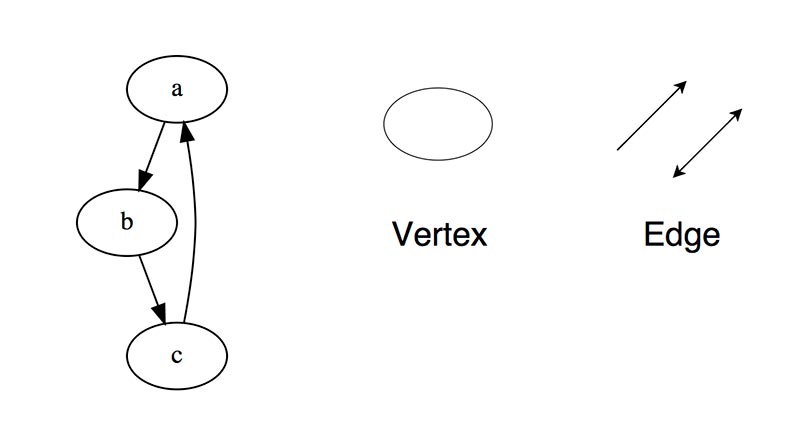
Бывают
Ориентированный, ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.
Неориентированные, к каждому из ребер можно осуществлять переход в обоих направлениях.
Смешанные
Встречаются в таких формах как
- Матрица смежности
- Список смежности
Общие алгоритмы обхода графа
- Поиск в ширину – обход по уровням
- Поиск в глубину – обход по вершинам
Вопросы
- Реализовать поиск по ширине и глубине
- Проверить является ли граф деревом или нет
- Посчитать количество ребер в графе
- Найти кратчайший путь между двумя вершинами
Деревья
Дерево-это иерархическая структура данных, состоящая из узлов (вершин) и ребер (дуг). Деревья по сути связанные графы без циклов.
Древовидные структуры везде и всюду. Дерево скилов в играх знают все.
Простое дерево
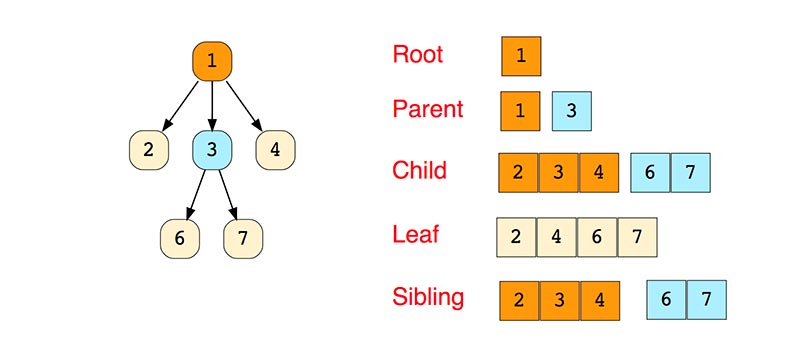
Типы деревьев
- N дерево
- Сбалансированное дерево
- Бинарное дерево
- Дерево Бинарного Поиска
- AVL дерево
- 2-3-4 деревья
Бинарное дерево самое распространенное.
«Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. » — Procs
Три способа обхода дерева
- В прямом порядке (сверху вниз) — префиксная форма.
- В симметричном порядке (слева направо) — инфиксная форма.
- В обратном порядке (снизу вверх) — постфиксная форма.
Вопросы
- Найти высоту бинарного дерева
- Найти N наименьший элемент в двоичном дереве поиска
- Найти узлы на расстоянии N от корня
- Найти предков N узла в двоичном дереве
Trie ( префиксное деревое )
Разновидность дерева для строк, быстрый поиск. Словари. Т9.
Вот как такое дерево хранит слова «top», «thus» и «their».
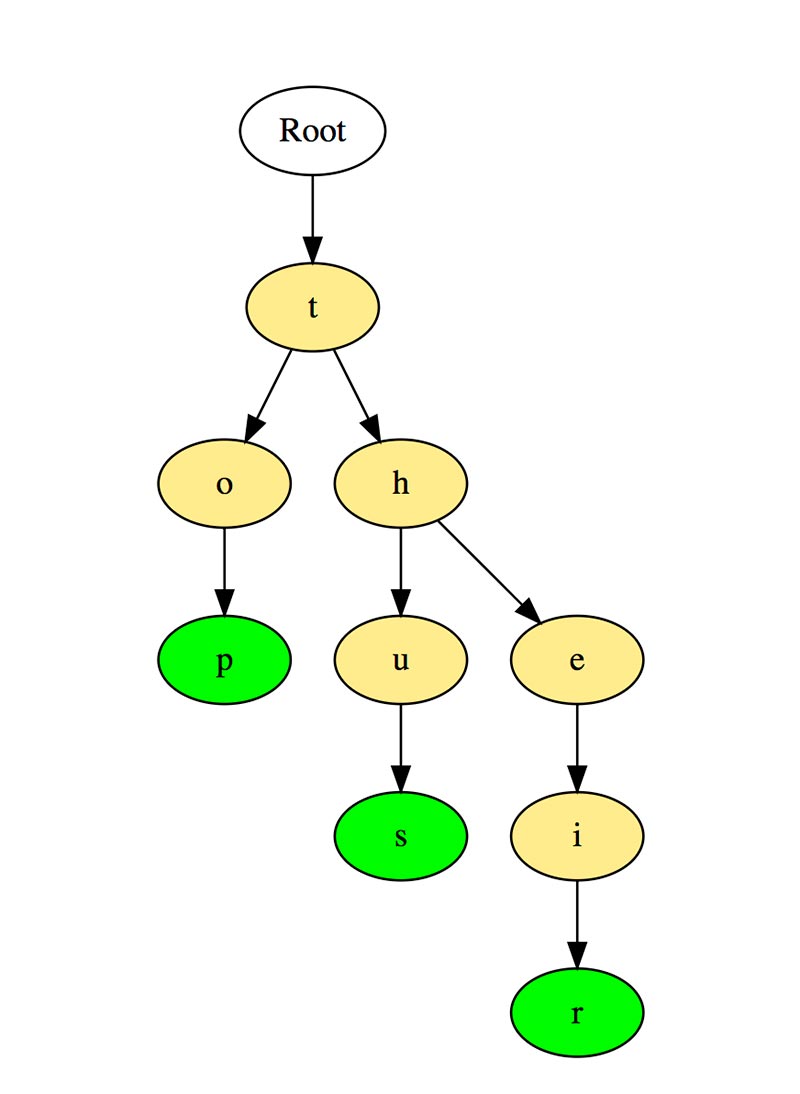
Слова хранятся сверху вниз, зеленые цветные узлы «p», «s» и «r» указывают на конец «top», «thus « и «their» соответственно.
Вопросы
- Подсчитать общее количество слов
- Вывести все слова
- Сортировка элементов массива с префиксного дерева
- Создание словаря T9
Хэш таблицы
Хэширование — это процесс, используемый для уникальной идентификации объектов и хранения каждого объекта в заранее рассчитанном уникальном индексе (ключе).
Объект хранится в виде пары «ключ-значение», а коллекция таких элементов называется «словарем». Каждый объект можно найти с помощью этого ключа.
По сути это массив, в котором ключ представлен в виде хеш-функции.
Эффективность хеширования зависит от
- Функции хеширования
- Размера хэш-таблицы
- Метода борьбы с коллизиями
Пример сопоставления хеша в массиве. Индекс этого массива вычисляется через хэш-функцию.
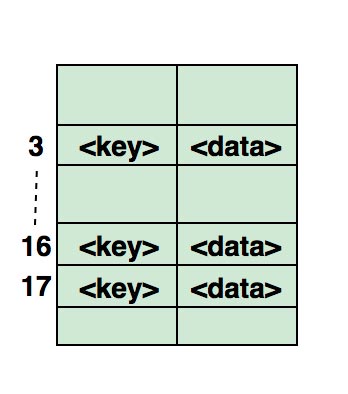
Вопросы
- Найти симметричные пары в массиве
- Найти, если массив является подмножеством другого массива
- Описать открытое хеширование
Список ресурсов
- medium.freecodecamp.org/the-top-data-structures-you-should-know-for-your-next-coding-interview-36af0831f5e3
- www.geeksforgeeks.org/commonly-asked-data-structure-interview-questions-set-1
- prog-cpp.ru/data-list
- habr.com/post/267855
- habr.com/post/273687
- habr.com/post/150732
- ruhighload.com/%D0%A7%D1%82%D0%BE+%D1%82%D0%B0%D0%BA%D0%BE%D0%B5+%D1%85%D0%B5%D1%88-%D1%82%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D1%8B+%D0%B8+%D0%BA%D0%B0%D0%BA+%D0%BE%D0%BD%D0%B8+%D1%80%D0%B0%D0%B1%D0%BE%D1%82%D0%B0%D1%8E%D1%82
- ru.wikipedia.org
Вместо заключения
Матчасть так же интересна, как и сами языки. Возможно, кто-то увидит знакомые ему базовые структуры и заинтересуется.
Спасибо, что прочли. Надеюсь не зря потратили время =)
Автор: demet






